Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Forever_Man Astazi la 11:51
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Joi 21 Noi 2024, 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la eugen în Ce fel de popor suntem
( 1 )
» Mesaj de la CAdi în OZN in Romania
( 1 )
» Mesaj de la virgil în Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7964) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Dacu2 | ||||
| Forever_Man | ||||
| Abel Cavaşi | ||||
| Meteorr |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| virgil | ||||
| Dacu2 | ||||
| Meteorr | ||||
| ilasus | ||||
| CAdi | ||||
| Abel Cavaşi | ||||
| eugen |
Spune şi altora
Cine este conectat?
În total sunt 22 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 22 Vizitatori Nici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Test de primalitate
Pagina 1 din 1
 Test de primalitate
Test de primalitate
Una din problemele calculării numerelor prime este dificultatea de a stabili primalitatea lor pentru numere extrem de mari. Chiar și cu ajutorul super calculatoarelor, testele de primalitate existente în prezent impune, fie calcularea unor numere mult mai mari pentru a stabili primalitatea unui număr mai mic, ca în cazul teoremei lui Wilson sau a micii teoreme a lui Fermat , fie un număr impresionant de calcule.
Propun în acest topic un test ceva mai simplu, dar care trebuie demonstrat.
Pentru valorile pe care le-am calculat testul este valabil.
Nu l-am verificat pentru toate numerele consecutive până la valoarea la care am calculat, ci le-am luat aleatoriu fără să găsesc un contra exemplu.
Un număr n este prim dacă atât valoarea(n-2)}{2}-1}) , cât și valoarea
, cât și valoarea (n-2)(n-3))}{3}+1}) se divid cu n. Dacă cel puțin una dintre ele nu se divide cu n, atunci n nu este un număr prim.
se divid cu n. Dacă cel puțin una dintre ele nu se divide cu n, atunci n nu este un număr prim.
Însă afirmația de mai sus trebuie demonstrată.
Personal, îi văd o utilitate practică ridicată pentru stabilirea primalității unui număr, mai ales pentru numerele foarte mari calculate cu ajutorul calculatorului.
Presupunând că afirmația de mai sus ar fi falsă, probabilitatea ca n să fie prim crește proporțional, dacă și valoarea(n-2)(n-3)(n-4)}{4}-1}) se divide cu n.
se divide cu n.
Cu siguranță este prim dacă pentru orice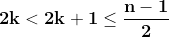 toate numerele obținute prin formulele :
toate numerele obținute prin formulele : }{(2k+1)!}+1}) și
și }{(2k)!}-1}) se divid cu n.
se divid cu n.
Eu cred totuși că este suficientă doar calcularea valorilor(n-2)}{2}-1}) și a valorii
și a valorii (n-2)(n-3))}{3}+1}) .
.
Propun în acest topic un test ceva mai simplu, dar care trebuie demonstrat.
Pentru valorile pe care le-am calculat testul este valabil.
Nu l-am verificat pentru toate numerele consecutive până la valoarea la care am calculat, ci le-am luat aleatoriu fără să găsesc un contra exemplu.
Un număr n este prim dacă atât valoarea
Însă afirmația de mai sus trebuie demonstrată.
Personal, îi văd o utilitate practică ridicată pentru stabilirea primalității unui număr, mai ales pentru numerele foarte mari calculate cu ajutorul calculatorului.
Presupunând că afirmația de mai sus ar fi falsă, probabilitatea ca n să fie prim crește proporțional, dacă și valoarea
Cu siguranță este prim dacă pentru orice
Eu cred totuși că este suficientă doar calcularea valorilor
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Test de primalitate
Re: Test de primalitate
De fapt prima, (n-2)}{2}-1}) se divide cu orice n număr impar .
se divide cu orice n număr impar .
Ar însemna că testul se rezumă doar la a calcula dacă(n-2)(n-3)}{3}+1}) se divide cu n.
se divide cu n.
Dacă nu se divide, n nu este un număr prim.
Dacă se divide cu n, atunci n este număr prim.
Mai trebuie verificat o idee prin calcul, după care să încercăm să și demonstrăm asta.
Și cred că se poate și demonstra.
Ar însemna că testul se rezumă doar la a calcula dacă
Dacă nu se divide, n nu este un număr prim.
Dacă se divide cu n, atunci n este număr prim.
Mai trebuie verificat o idee prin calcul, după care să încercăm să și demonstrăm asta.
Și cred că se poate și demonstra.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Test de primalitate
Re: Test de primalitate
Da... eu am calculat pentru numerele care nu sunt prime.
Am găsit exemple pentru n prim care nu divide, dar nu am găsit contraexemple pentru n nonprim care divide.
O să încerc să găsesc explicația.
Am găsit exemple pentru n prim care nu divide, dar nu am găsit contraexemple pentru n nonprim care divide.
O să încerc să găsesc explicația.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Test de primalitate
Re: Test de primalitate
Am luat la calculat valorile consecutive până pe la vreo 500.
Concluzia la care am ajuns este următoarea, ca și regulă generală :
Fie p cel mai mic număr prim care divide un număr natural n.
Pentru orice număr par 2k și număr impar 2k+1, astfel încât}) , dacă n nu este un număr prim atunci nu divide niciuna din valorile:
, dacă n nu este un număr prim atunci nu divide niciuna din valorile:
}{(2k)!}-1}) sau/și
sau/și }{(2k+1)!}+1})
Sau mai simplu spus, dacă p este cel mai mic număr prim care divide n, atunci pentru m > p, orice valoare obținută prin formula
(n-2)(n-3)...(n-m)}{m!}\pm 1})
se divide cu n , iar pentru\leq p}) nu se divide cu n, dacă n nu este număr prim.
nu se divide cu n, dacă n nu este număr prim.
(n-2)(n-3)...(n-(m+1))(n-(m+2))...}{m!}\pm 1 })
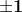 este pentru generalizare, iar semnul este dat de paritatea lui m. Dacă m este un număr par semnul va fi minus, dacă m este un număr impar, semnul va fi plus.
este pentru generalizare, iar semnul este dat de paritatea lui m. Dacă m este un număr par semnul va fi minus, dacă m este un număr impar, semnul va fi plus.
Un caz mai mult sau mai puțin particular îl reprezintă valoarea lui n un număr prim, caz în care pentru orice m>1 formula se divide cu n, dacă acesta este prim. Generalizarea enunțului este valabilă și pentru cazul n număr prim, pentru că acesta nu are divizori, cel mai mic număr prim care îl divide este el însuși (1 nefiind considerat prim), situație în care prima valoare pe care trebuie să o aibă m ca formula să nu se dividă cu p(adică n) este chiar p(adică n).
Câteva exemple pentru a înțelege mai bine raționamentul.
Calculăm spre exemplu, numărul 25. Cel mai mic număr prim care divide 25 este 5. Din enunț reiese că pentru orice m mai mic decât 5, rezultatul obținut de formluă se divide cu 25 :
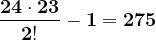
Rezultatul se divide cu 25.
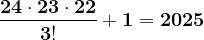
Rezultatul se divide cu 25
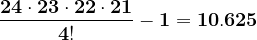
Rezultatul se divide cu 25.
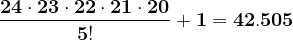
Rezultatul nu se mai divide cu 25.
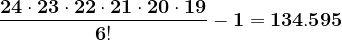
Nici în acest caz rezultatul nu se mai divide cu 25, ca de altfel pentru orice valoare am continua să calculăm.
În cazul lui n=121, spre exemplu, cel mai mic număr prim care divide n este 11. Pentru orice m mai mic ca 11, valoarea formulelor se divide cu 121. Pentru m mai mare sau egal cu 11, valoarea obținută prin formulele de mai sus nu se mai divide cu 121.
Desigur, am dat ca exemple doar pătrate perfecte, dar se poate calcula pentru orice alt număr. Condiția pentru care valoarea obținută prin cele două formule(cu plus și minus 1) nu se mai divide cu n dacă acesta nu este prim,
este ca m (din formulă) să fie mai mare sau egal cu cel mai mic număr prim care divide n.
Această observație este totuși destul de interesantă, poate chiar și importantă, pentru că utilitatea ei practică apare în momentul în care avem nevoie să știm care este cel mai mic număr prim care divide un număr, spre exemplu.
Concluzia la care am ajuns este următoarea, ca și regulă generală :
Fie p cel mai mic număr prim care divide un număr natural n.
Pentru orice număr par 2k și număr impar 2k+1, astfel încât
Sau mai simplu spus, dacă p este cel mai mic număr prim care divide n, atunci pentru m > p, orice valoare obținută prin formula
se divide cu n , iar pentru
Un caz mai mult sau mai puțin particular îl reprezintă valoarea lui n un număr prim, caz în care pentru orice m>1 formula se divide cu n, dacă acesta este prim. Generalizarea enunțului este valabilă și pentru cazul n număr prim, pentru că acesta nu are divizori, cel mai mic număr prim care îl divide este el însuși (1 nefiind considerat prim), situație în care prima valoare pe care trebuie să o aibă m ca formula să nu se dividă cu p(adică n) este chiar p(adică n).
Câteva exemple pentru a înțelege mai bine raționamentul.
Calculăm spre exemplu, numărul 25. Cel mai mic număr prim care divide 25 este 5. Din enunț reiese că pentru orice m mai mic decât 5, rezultatul obținut de formluă se divide cu 25 :
Rezultatul se divide cu 25.
Rezultatul se divide cu 25
Rezultatul se divide cu 25.
Rezultatul nu se mai divide cu 25.
Nici în acest caz rezultatul nu se mai divide cu 25, ca de altfel pentru orice valoare am continua să calculăm.
În cazul lui n=121, spre exemplu, cel mai mic număr prim care divide n este 11. Pentru orice m mai mic ca 11, valoarea formulelor se divide cu 121. Pentru m mai mare sau egal cu 11, valoarea obținută prin formulele de mai sus nu se mai divide cu 121.
Desigur, am dat ca exemple doar pătrate perfecte, dar se poate calcula pentru orice alt număr. Condiția pentru care valoarea obținută prin cele două formule(cu plus și minus 1) nu se mai divide cu n dacă acesta nu este prim,
este ca m (din formulă) să fie mai mare sau egal cu cel mai mic număr prim care divide n.
Această observație este totuși destul de interesantă, poate chiar și importantă, pentru că utilitatea ei practică apare în momentul în care avem nevoie să știm care este cel mai mic număr prim care divide un număr, spre exemplu.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 