Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Meteorr Ieri la 21:34
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Joi 21 Noi 2024, 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la Abel Cavaşi în Daci nemuritori
( 1 )
» Mesaj de la CAdi în Fenomene Electromagnetice
( 1 )
» Mesaj de la virgil în Fiinte deosebite.
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Dacu2 | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Abel Cavaşi |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| virgil | ||||
| Dacu2 | ||||
| Meteorr | ||||
| ilasus | ||||
| CAdi | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 47 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 47 Vizitatori :: 1 Motor de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
O alta ecuatie cu factoriale
2 participanți
Pagina 1 din 1
 O alta ecuatie cu factoriale
O alta ecuatie cu factoriale
Sa se rezolve in multimea numerelor naturale ecuatia 
_________________
"La inceput era CUVANTUL si CUVANTUL era la DUMNEZEU si DUMNEZEU era CUVANTUL."
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: O alta ecuatie cu factoriale
Re: O alta ecuatie cu factoriale
Singura solutie pe care am gasit-o eu este 3.
Pentru ca:
n! este:
1!=1
2!=2
3!=6
4!=24
5!=120
6!=720
...
Pentru n mai mare sau egal cu 5, factorialul sau este un numar care se termina cu 0, ceea ce determina ca suma factorialelor pana la n, pentru n mai mare sau egal cu 4, este un numar care se termina cu cifra 3, adica un numar impar:
4!=33
5!=153
6!=873
...
Din enuntul tau, trebuie gasita solutia naturala pentru
})
Pentru x numar par orice putere a sa este un numar par si iese din discutie intrucat ultima sa cifra nu este 3.
Deci raman de analizat doar numerele impare.
calculand, observam ca 3! este egal cu 9, adica}=9) si reprezinta o solutie a ecuatiei tale.
si reprezinta o solutie a ecuatiei tale.
Ar mai putea fi alta?
Raspunsul este nu pentru ca:
Puterea unui numar de forma se termina intotdeauna cu 1, deci pentru x un numar impar care se termina cu 1, orice putere a sa nu se termina cu trei, deci nici un numar de acest fel nu poate fi solutia ecuatiei tale.
se termina intotdeauna cu 1, deci pentru x un numar impar care se termina cu 1, orice putere a sa nu se termina cu trei, deci nici un numar de acest fel nu poate fi solutia ecuatiei tale.
Puterea unui numar de forma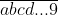 se termina fie cu cifra 9, fie cu cifra 1, deci nici in acest caz, niciun numar impar care se termina cu 9 nu poate fi solutia ecuatiei tale.
se termina fie cu cifra 9, fie cu cifra 1, deci nici in acest caz, niciun numar impar care se termina cu 9 nu poate fi solutia ecuatiei tale.
Pentru un numar de forma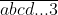 puterea acestui numar care s-ar putea termina in cifra 3 trebuie sa aiba un exponent de forma 4k+1, dar acesta este un numar impar si nu poate fi solutia ecuatiei pe care ai dat-o pentru ca din datele tale rezulta ca daca x este impar, exponentul sau trebuie sa fie par(x-1).
puterea acestui numar care s-ar putea termina in cifra 3 trebuie sa aiba un exponent de forma 4k+1, dar acesta este un numar impar si nu poate fi solutia ecuatiei pe care ai dat-o pentru ca din datele tale rezulta ca daca x este impar, exponentul sau trebuie sa fie par(x-1).
Pentru un numar de forma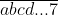 observam si in acest caz ca puterea care s-ar termina in cifra trei trebuie sa aiba exponentul de forma 4k-1, deci si in acest caz exponentul este un numar impar si prin rationamentul pe care ti l-am aratat mai sus, niciun numar impar care se termina in cifra 7 nu poate fi solutie a ecuatiei tale.
observam si in acest caz ca puterea care s-ar termina in cifra trei trebuie sa aiba exponentul de forma 4k-1, deci si in acest caz exponentul este un numar impar si prin rationamentul pe care ti l-am aratat mai sus, niciun numar impar care se termina in cifra 7 nu poate fi solutie a ecuatiei tale.
Bineinteles puterea unui numar impar care se termina cu 5 are ultima cifra 5 si iese din discutie.
Deci, orice numar cu exceptia lui 3 nu poate fi solutie a ecuatiei tale.
Pentru ca:
n! este:
1!=1
2!=2
3!=6
4!=24
5!=120
6!=720
...
Pentru n mai mare sau egal cu 5, factorialul sau este un numar care se termina cu 0, ceea ce determina ca suma factorialelor pana la n, pentru n mai mare sau egal cu 4, este un numar care se termina cu cifra 3, adica un numar impar:
4!=33
5!=153
6!=873
...
Din enuntul tau, trebuie gasita solutia naturala pentru
Pentru x numar par orice putere a sa este un numar par si iese din discutie intrucat ultima sa cifra nu este 3.
Deci raman de analizat doar numerele impare.
calculand, observam ca 3! este egal cu 9, adica
Ar mai putea fi alta?
Raspunsul este nu pentru ca:
Puterea unui numar de forma
Puterea unui numar de forma
Pentru un numar de forma
Pentru un numar de forma
Bineinteles puterea unui numar impar care se termina cu 5 are ultima cifra 5 si iese din discutie.
Deci, orice numar cu exceptia lui 3 nu poate fi solutie a ecuatiei tale.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: O alta ecuatie cu factoriale
Re: O alta ecuatie cu factoriale
x=1 nu este solutie???????Evident ca x trebuie sa fie un numar impar...... 
_________________
"La inceput era CUVANTUL si CUVANTUL era la DUMNEZEU si DUMNEZEU era CUVANTUL."
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: O alta ecuatie cu factoriale
Re: O alta ecuatie cu factoriale
De fapt si 2 este o solutie.
Sa conchidem.
Solutiile nu pot fi decat 1, 2 si 3.
Sa conchidem.
Solutiile nu pot fi decat 1, 2 si 3.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: O alta ecuatie cu factoriale
Re: O alta ecuatie cu factoriale
Nu, gresesc !
Se pareca ma incurc in lucrurile simple.
Se pareca ma incurc in lucrurile simple.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: O alta ecuatie cu factoriale
Re: O alta ecuatie cu factoriale
Solutiile in multimea numerelor naturale sunt x=1 si x=3.curiosul a scris:De fapt si 2 este o solutie.
Sa conchidem.
Solutiile nu pot fi decat 1, 2 si 3.
_________________
"La inceput era CUVANTUL si CUVANTUL era la DUMNEZEU si DUMNEZEU era CUVANTUL."
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 