O inecuatie cu modul

Scris de **AMOT** Sam 31 Mar 2012, 18:58

Sa se rezolve inecuatia $O inecuatie cu modul Mimetex$ unde $O inecuatie cu modul Mimetex$ .

Scris de **meteor** Sam 31 Mar 2012, 23:05

Parca ai adus cindva o "demonstratie" ce spune ca intre numerele complexe (cu partea imaginara nenula) nu exista relatii de ordine?!....

Scris de **omuldinluna** Sam 31 Mar 2012, 23:19

Pare legimita intrebarea lui AMOT, caci modulul e un numar real. Cred ca problema se traduce ca:

$O inecuatie cu modul Mimetex$ (0)

Ceea ce este la fel de bine:

$O inecuatie cu modul Mimetex$ (1)

Desfacem paranteza si obtinem, daca algebra mea nu ma lasa la greu:

$O inecuatie cu modul Mimetex$ (2)

Adica:

$O inecuatie cu modul Mimetex$ (3)

In aceste conditii, x trebuie sa fie clar un numar pur imaginar, iar in acelasi timp trebuie sa avem:

$O inecuatie cu modul Mimetex$ (4)

Problema este ca in momentul in care am efectuat scrierea (1), am considerat cantitatea de sub radical pozitiva, ori impunand ca x sa fie pur imaginar ea este neaparat negativa. E tarziu si inca mai am de lucru, recunosc faptul ca momentan nu-mi dau seama daca problema nu are solutie sau am gresit eu ceva (daca punem la plesneala x=i, obtinem un rezultat bun, chiar din forma scrisa sub modul).

Scris de **omuldinluna** Sam 31 Mar 2012, 23:54

Mda, solutie pentru x real nu exista caci ne conduce la necesitatea contradictorie ca x sa fie pur imaginar, iar presupunand de la inceput o solutie pur imaginara inegalitatile isi pierd sensul, caci intr-adevar intre numere complexe (cu parte imaginara nenula) nu exista relatii de ordine si totusi x=i satisface inecuatia scrisa de AMOT.

Am gresit eu ceva?

Scris de curiosul Dum 01 Apr 2012, 08:25

Eu as zice ca trebuie desfcaut modulul ecuatiei
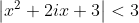$\left | x^{2}+2ix+3 \right |< 3$ .

Deci
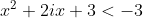
$x^{2}+2ix+3< 3$
si
$x^{2}+2ix+3<-3$

S-a ajuns la doua inecuatii de gradul 2.
Folosesc expresia omuluidinluna, iar daca algebra mea nu ma lasa la greu, continuarea ar fi:

Cazul 1.
$x^{2}+2ix+3< 3$
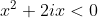
$x^{2}+2ix < 0$
si as rezolva-o prin delta:
$\Delta =4i^{2}-4=4\left ( i^{2}-1 \right )$
Apar doua cazuri:
1a. daca inlocuim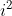 $i^{2}$ cu -1, 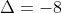$\Delta =-8$ si ecuatia nu are solutii reale.
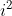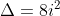
1b.Daca inlocuim -1 cu $i^{2}$ , $\Delta =8i^{2}$
Pentru cazul 1b. solutiile sunt
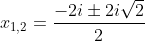
$x_{1,2}=\frac{-2i\pm 2i\sqrt{2}}{2}$
deci
$x_{1}=-i\left ( 1+\sqrt{2} \right )$
si
$x_{1}=i\left (\sqrt{2}-1 \right )$

Cazul 2.
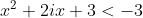
$x^{2}+2ix+3< -3$
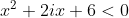$x^{2}+2ix+6<0$ , caz pentru care $\Delta =4i^{2}-24=4\left ( i^{2}-6 \right )$
iar solutiile:
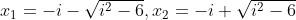
$x_{1}=-i-\sqrt{i^{2}-6},x_{2}=-i+\sqrt{i^{2}-6}$
Oricum, ecuatia nu are solutii reale, iar exprimarea lor ca si solutii complexe o poti face inlocuind -6 cu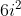 $6i^{2}$ , spre exemplu unde poti scoate factor comun pe i, si sa faci reuniunea intervalelor pentru care ecuatia ar avea solutii.
Dar parerea mea este ca ecuatia nu are sens.
Astept sa revina AMOT sa ne corecteze pe amandoi.
Chiar sunt curios unde este gresit rationamentul meu.

Scris de **AMOT** Dum 01 Apr 2012, 08:34

Sa rationam logic!!!!!! Rolling Eyes

Care este definitia modulului unui numar???? Rolling Eyes

Scris de curiosul Dum 01 Apr 2012, 08:40

$\left | a \right |=a,\left | -a \right |=a$

In cazul 2 pe care ti l-am aratat, am inlociut a cu ecuatia ta, dupa carte am inmultit cu -1 toata ecuatia si asa am ajuns la cele doua cazuri.
E gresit?

Scris de **AMOT** Dum 01 Apr 2012, 08:42

curiosul a scris: $\left | a \right |=a,\left | -a \right |=a$

In cazul 2 pe care ti l-am aratat, am inlociut a cu ecuatia ta, dupa carte am inmultit cu -1 toata ecuatia si asa am ajuns la cele doua cazuri.
E gresit?

Cine este a???? Rolling Eyes

Scris de **AMOT** Dum 01 Apr 2012, 08:46

omuldinluna a scris:Pare legimita intrebarea lui AMOT, caci modulul e un numar real. Cred ca problema se traduce ca:
$O inecuatie cu modul Mimetex$ (0)

Cum ai ajuns la aceasta traducere?????? Rolling Eyes

Scris de **AMOT** Dum 01 Apr 2012, 08:48

meteor a scris:Parca ai adus cindva o "demonstratie" ce spune ca intre numerele complexe (cu partea imaginara nenula) nu exista relatii de ordine?!....

Intr-adevar in multimea numerelor complexe cu partea imaginara nenula nu exista relatie de ordine si ce are a face asta cu inecuatia ce se cere de rezolvat????? Rolling Eyes

Scris de curiosul Dum 01 Apr 2012, 08:52

Amot, lasa stilul asta.
a este un crocodil cu blana ultraviolet de mare.
Atat omuldinluna cat si eu am incercat sa-ti dezvoltam subiectul.
Daca ai ceva de scris/spus referitor la ce am scris noi, bine, daca nu la fel de bine.
Scrie solutia pe care o ai tu si nu mai tot intreba atat.
Nu ai deloc bunavointa sa apreciezi ca cineva vrea sa "te ajute" .
De fapt, tu pentru ce ai scris inecuatia?
Ai nevoie de raspuns, de solutii, sau ai nevoie de un subiect in care sa incepi sa-ti faci numarul?
Ai dreptate, nu e corect ceea ce am scris.
Dar ma gandeam ca ar trebui cineva sa scie totusi ceva in acest subiect, daca tu nu scrii nimic.

Scris de **AMOT** Dum 01 Apr 2012, 09:03

omuldinluna a scris:Mda, solutie pentru x real nu exista caci ne conduce la necesitatea contradictorie ca x sa fie pur imaginar, iar presupunand de la inceput o solutie pur imaginara inegalitatile isi pierd sensul, caci intr-adevar intre numere complexe (cu parte imaginara nenula) nu exista relatii de ordine si totusi x=i satisface inecuatia scrisa de AMOT.

Am gresit eu ceva?

$O inecuatie cu modul Mimetex$ este una din infinitatea de solutii ale acelei inecuatii.Inecuatia are sens! Rolling Eyes

Scris de **AMOT** Dum 01 Apr 2012, 09:09

curiosul a scris:Amot, lasa stilul asta.
a este un crocodil cu blana ultraviolet de mare.
Atat omuldinluna cat si eu am incercat sa-ti dezvoltam subiectul.
Daca ai ceva de scris/spus referitor la ce am scris noi, bine, daca nu la fel de bine.
Scrie solutia pe care o ai tu si nu mai tot intreba atat.
Nu ai deloc bunavointa sa apreciezi ca cineva vrea sa "te ajute" .
De fapt, tu pentru ce ai scris inecuatia?
Ai nevoie de raspuns, de solutii, sau ai nevoie de un subiect in care sa incepi sa-ti faci numarul?
Ai dreptate, nu e corect ceea ce am scris.
Dar ma gandeam ca ar trebui cineva sa scie totusi ceva in acest subiect, daca tu nu scrii nimic.

Eu stiu raspunsul dar vreau sa vad daca raspunsul tau si al celorlalti este acelasi cu al meu....... Rolling Eyes

Eu vorbesc decent.......Aceasta inecuatie presupune cercetare si avand raspunsurile voastre fie si gresite total sau partial gresite sau incomplete ma pot ajuta sa inteleg mai bine matematica si astfel sa ma perfectionez....... Rolling Eyes

Scris de curiosul Dum 01 Apr 2012, 09:17

Pai si eu la fel.
Cum imi dau seama ca "rezolvarea" mea este gresita, daca tu pui numai intrebari fara sa explici macar de ce crezi ca este sau nu gresit, din punctul tau de vedere ?
Si..!!!??? Rolling Eyes

... vorbesc decent.
Nu crezi? Rolling Eyes

Scris de **AMOT** Dum 01 Apr 2012, 09:20

curiosul a scris:Pai si eu la fel.
Cum imi dau seama ca "rezolvarea" mea este gresita, daca tu pui numai intrebari fara sa explici macar de ce crezi ca este sau nu gresit, din punctul tau de vedere ?
Si..!!!??? ... vorbesc decent.
Nu crezi?

Eu te-ntreb si tu raspunzi!Care este definitia modulului unui numar?

Scris de **omuldinluna** Dum 01 Apr 2012, 11:13

Curiosule, modulul unui numar complex este definit astfel:

daca

$O inecuatie cu modul Mimetex$ , unde a si b sunt numere reale iar pe b il luam deocamdata diferit de 0, atunci

$O inecuatie cu modul Mimetex$ , unde prin * inteleg operatia de conjugare complexa a lui x, care da $O inecuatie cu modul Mimetex$ , ceea ce conduce la

$O inecuatie cu modul Mimetex$

Daca b=0, gasim imediat ceea ce ai scris tu, valabil pentru numere reale.

Scris de curiosul Dum 01 Apr 2012, 12:04

Ok. Capisco.
Iar explicatia ta raspunde si la intrebarea lui AMOT pentru tine.
Multumesc.

Scris de **AMOT** Dum 01 Apr 2012, 16:33

Exista modulul unui numar real si modulul unui numar complex.......Se observa imediat ca nu putem vorbi despre modulul unui numar complex in cazul acestei inecuatii deoarece s-ar ajunge la concluzia ca patratul unui numar ar fi mai mic ca zero ceea ce este absurd si omuldinluna nu a aobservat acest fapt dar a sesizat corect ca numarul imaginar i este o solutie a inecuatiei...... Rolling Eyes

Toate solutiile inecuatiei sunt de forma $O inecuatie cu modul Mimetex$ unde a este un numar real si $O inecuatie cu modul Mimetex$ astfel incat sa vorbim despre modulul unui numar real.Care sunt valorile lui a pentru care inecuatia are solutii????? Rolling Eyes

Scris de Continut sponsorizat

O inecuatie cu modul

O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul

Re: O inecuatie cu modul