Ultimele subiecte
» Grup de cercetare pentru constiintaScris de CAdi Astazi la 05:08
» OZN in Romania
Scris de CAdi Ieri la 20:05
» Fotografia astronomica.
Scris de virgil Ieri la 19:32
» Structura atomului
Scris de virgil Lun 02 Sept 2024, 20:16
» Ce fel de popor suntem
Scris de eugen Lun 02 Sept 2024, 14:54
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Lun 02 Sept 2024, 07:45
» Unde a ajuns stiinta ?
Scris de virgil Mar 27 Aug 2024, 17:55
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de CAdi Lun 26 Aug 2024, 15:08
» URME ALE EXTRATERESTRILOR PE PAMANT. DESCOPERIRI INEXPLICABILE SI FENOMENE OZN 1
Scris de CAdi Dum 25 Aug 2024, 23:21
» PROFILUL CERCETATORULUI...
Scris de eugen Dum 25 Aug 2024, 11:27
» Experimentul Pound Rebka
Scris de virgil Lun 19 Aug 2024, 18:14
» Microundele
Scris de CAdi Vin 16 Aug 2024, 11:11
» Transilvania-pamant stramosesc
Scris de CAdi Mier 14 Aug 2024, 06:55
» Basarabia, Bucovina - pământ românesc
Scris de CAdi Mar 13 Aug 2024, 11:54
» Scrierea dacilor
Scris de CAdi Lun 12 Aug 2024, 19:58
» Sanatate- Diverse
Scris de eugen Sam 10 Aug 2024, 10:01
» Daci nemuritori
Scris de eugen Vin 09 Aug 2024, 22:10
» Suntem indexaţi de motoarele de căutare?
Scris de CAdi Mar 06 Aug 2024, 15:58
» Impulsul elicoidal
Scris de virgil Joi 01 Aug 2024, 21:01
» Constatari
Scris de CAdi Joi 01 Aug 2024, 06:36
» New topic
Scris de ilasus Mier 31 Iul 2024, 20:54
» Globalizarea
Scris de eugen Sam 27 Iul 2024, 12:44
» Fenomene Electromagnetice
Scris de eugen Lun 22 Iul 2024, 21:37
» Sa mai auzim si de bine in Romania :
Scris de virgil Lun 22 Iul 2024, 18:39
» Masina Timpului
Scris de CAdi Lun 22 Iul 2024, 13:17
» Ce este FOIP?
Scris de Abel Cavaşi Vin 19 Iul 2024, 22:02
» Inertia
Scris de virgil Mier 17 Iul 2024, 11:09
» Lucrul mecanic - definitie si exemple (Secţiunea 2)
Scris de CAdi Mar 16 Iul 2024, 05:20
» Laborator-sa construim impreuna
Scris de eugen Lun 15 Iul 2024, 10:17
» Stanley A. Meyer - Hidrogen
Scris de eugen Dum 14 Iul 2024, 20:25
Postări cu cele mai multe reacții ale lunii
» Mesaj de la Razvan în Fotografia astronomica. ( 3 )
» Mesaj de la Razvan în Fotografia astronomica.
( 2 )
» Mesaj de la eugen în Ce fel de popor suntem
( 2 )
» Mesaj de la CAdi în Structura atomului
( 1 )
» Mesaj de la Razvan în Fotografia astronomica.
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12369) | ||||
| CAdi (12260) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7952) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6170) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3910) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Spune şi altora
Cine este conectat?
În total sunt 40 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 40 Vizitatori :: 2 Motoare de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Integrarea cuaternionilor
3 participanți
Pagina 2 din 2
Pagina 2 din 2 •  1, 2
1, 2
 Integrarea cuaternionilor
Integrarea cuaternionilor
Rezumarea primului mesaj :
Provine din topicul Teste propuse la matematică
Va propun spre discutie o problema care ma "doare" de cateva zile.
Cum integrez o forma algebrica de forma:

unde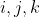 -bazele unui cvaternion si ultimul
-bazele unui cvaternion si ultimul  baza numarului complex.
baza numarului complex.
Se poate da solutia:

Daca da de ce da daca nu de ce nu,si in acest ultim caz care ar fi solutia si de ce ?
Provine din topicul Teste propuse la matematică
Va propun spre discutie o problema care ma "doare" de cateva zile.
Cum integrez o forma algebrica de forma:
unde
Se poate da solutia:
Daca da de ce da daca nu de ce nu,si in acest ultim caz care ar fi solutia si de ce ?
Ultima editare efectuata de catre Razvan in Lun 14 Ian 2013, 21:01, editata de 1 ori (Motiv : Provine din ...)
Vizitator- Vizitator
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Îmi pare rău dar am impresia că tu confunzi raza vectoare a numărului complex care,repet,se reprezintă ca fiind un punct in sistemul de axe ortogonale una pentru partea reala şi alta pentru partea imaginară a acelui număr complex.Un vector  se reprezintă in sistemul de axe ortogonale XOX si YOY ca fiind un segment orientat de dreaptă unde
se reprezintă in sistemul de axe ortogonale XOX si YOY ca fiind un segment orientat de dreaptă unde  sunt versorii acestor axe XOX si YOY.
sunt versorii acestor axe XOX si YOY.
1. Te rog să reprezinţi grafic numărul complex .
.
2. Te rog să reprezinţi grafic şi vectorul care are originea în punctul de coordonate A(-5,2).
care are originea în punctul de coordonate A(-5,2).
Fă te rog desenele respective şi ai să-ţi dai seama unde greşesti.
Geometric vorbind numărul complex este de fapt afixul punctului de coordonate M(a,b) iar raza vectoare a punctului M(a,b) este un vector de poziţie a numărului complex respectiv ceea ce nu înseamnă că un număr complex este un vector aşa cum afirmi tu care mai susţii şi faptul că
este de fapt afixul punctului de coordonate M(a,b) iar raza vectoare a punctului M(a,b) este un vector de poziţie a numărului complex respectiv ceea ce nu înseamnă că un număr complex este un vector aşa cum afirmi tu care mai susţii şi faptul că  ar fi versorii axelor din sistemul de axe ortogonale de reprezentare a numerelor complexe unde
ar fi versorii axelor din sistemul de axe ortogonale de reprezentare a numerelor complexe unde  este numărul imaginar.
este numărul imaginar.
Scuză-mă dar nu ştiu ce fel de matematică este asta!?
Aş dori şi alte păreri ale altor forumişti de aici care ştiu poate mai multă matematică decât noi doi.
1. Te rog să reprezinţi grafic numărul complex
2. Te rog să reprezinţi grafic şi vectorul
Fă te rog desenele respective şi ai să-ţi dai seama unde greşesti.
Geometric vorbind numărul complex
Scuză-mă dar nu ştiu ce fel de matematică este asta!?
Aş dori şi alte păreri ale altor forumişti de aici care ştiu poate mai multă matematică decât noi doi.
Dacu- Foarte activ

- Numarul mesajelor : 2613
Data de inscriere : 28/07/2012
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Hai ca am gasit ceva ce poate te lamureste:
http://lectura.bibliotecadigitala.ro/?p=1476
Pagina 8-exact definitia de care am vorbit si mai departe vorbeste si de translatia lor.
Vezi si tinem legatura
Vizitator- Vizitator
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Eu sunt lămurit demult şi te rog citeşte cu glas tare paragraful II.10. din link-ul dat de tine... 
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22205
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Paragraful II 10 nu aduce nimic nou in relatia vector -numar complex Se defineste imaginea geometrica si afixul alti termeni care o sa-i folosesca,nu vad ceva in sprijinul afirmatilor tale.Chiar din contra in acest paragraf defineste bijectia intre C si RxR
Iti redau definitia de interes:
Paragraful I 2 (pag 8 )
Cu titlul suficient de sugestiv:
DEFINITIA VECTORIALA A NUMARULUI COMPLEX
Definitie Numim numar complex orice vector OA unde A este un punct din planul euclidian.Multimea vectorilor cu originea in O se numeste corpul numerelor complexe
Negru pe alb
Iti redau definitia de interes:
Paragraful I 2 (pag 8 )
Cu titlul suficient de sugestiv:
DEFINITIA VECTORIALA A NUMARULUI COMPLEX
Definitie Numim numar complex orice vector OA unde A este un punct din planul euclidian.Multimea vectorilor cu originea in O se numeste corpul numerelor complexe
Negru pe alb
Vizitator- Vizitator
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Acea definiţie aşa zisă vectorială nu mi se pare corectă deoarece se confundă numărul complex z=a+bi cu raza vectoare OM , iar paragraful II.10. arată clar şi fără echivoc că numarul complex z=a+bi este afixul punctului M(a,b).Care este din punct de vedere matematic definiţia cuvântului afix?DEX spune clar ce este un afix.Dă te rog şi definiţia de la paragraful II.10. ca să vadă oricine şi să se lămurească odată ce este un număr complex şi ce este un vector sau o rază vectoare  .
.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22205
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Mezei Geza,
Dacă numerele complexe ar fi vectori atunci asta ar însemna că împărţirea a două numere complexe nu este permisă ceea ce orice elev de clasa X-a de la un liceeu de matematică ştie că nu este adevărat deoarece împărtirea a două numere complexe este de fapt permisă dar împărţirea a doi vectori oarecare nu este permisă.De ce împărţirea a doi vectori oarecare nu este permisă?
Dacă numerele complexe ar fi vectori atunci asta ar însemna că împărţirea a două numere complexe nu este permisă ceea ce orice elev de clasa X-a de la un liceeu de matematică ştie că nu este adevărat deoarece împărtirea a două numere complexe este de fapt permisă dar împărţirea a doi vectori oarecare nu este permisă.De ce împărţirea a doi vectori oarecare nu este permisă?
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22205
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Buna intrebare
Ca un elev de clasa a X-a ce stie si ce nu stie este treaba lui personala.O sa ajunga la facultate si o sa vada ca poate impartii si doi vectori daca le defineste corect.Ca se evita a se folosi impartirea vectorilor este alta problema.Se evita exact datorita posibilitatilor multiple de a definii un vector.De exemplu sub forma matriceala o impartire nu mai este corecta deoarece nu defineste unic solutia.
Dar sa revenim la oile noaste:
In cazul in care vectorii ii definesc sub forma:
Ce ma impiedica pe mine sa scriu : echivalent cu:
echivalent cu: 
Absolut nimic !! Ca este de preferat a se evita o astfel de scriere sunt deacord si am motivat mai sus.
Dar daca presupunem ca nu as avea alta solutie la indemana se poate si asa si rezultatul este corect
Exemplu

a=2 rezulta

echivalent cu:
 amplific cu numitorul efectuez calculele rezulta:
amplific cu numitorul efectuez calculele rezulta:

Repet pe cat posibil a se evita o astfel de scriere.
Nu am putut sa-ti copiez definitia ceruta,sunt virusat ieri nu ma lasat nimic Copy-Paste,vad ca azi ma mai lasa inca.O sa dau jos tot sistemul daca nu apar o vreme asta este motivul
Ca un elev de clasa a X-a ce stie si ce nu stie este treaba lui personala.O sa ajunga la facultate si o sa vada ca poate impartii si doi vectori daca le defineste corect.Ca se evita a se folosi impartirea vectorilor este alta problema.Se evita exact datorita posibilitatilor multiple de a definii un vector.De exemplu sub forma matriceala o impartire nu mai este corecta deoarece nu defineste unic solutia.
Dar sa revenim la oile noaste:
In cazul in care vectorii ii definesc sub forma:
Ce ma impiedica pe mine sa scriu :
Absolut nimic !! Ca este de preferat a se evita o astfel de scriere sunt deacord si am motivat mai sus.
Dar daca presupunem ca nu as avea alta solutie la indemana se poate si asa si rezultatul este corect
Exemplu
a=2 rezulta
echivalent cu:
Repet pe cat posibil a se evita o astfel de scriere.
Nu am putut sa-ti copiez definitia ceruta,sunt virusat ieri nu ma lasat nimic Copy-Paste,vad ca azi ma mai lasa inca.O sa dau jos tot sistemul daca nu apar o vreme asta este motivul
Vizitator- Vizitator
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Exemplu dat de tine este valabil pentru orice poziţie a vectorilor  ?Prin ce este caracterizat un vector?Tu crezi că ai definit bine acei vectori din exemplul de împărţire a lor dat de tine?Eu cred că ar trebui să revezi cu atenţie secţiunea din matematică care tratează vectorii altfel se poate ajunge la greşeli nepermise care vor avea efecte nebănuite.
?Prin ce este caracterizat un vector?Tu crezi că ai definit bine acei vectori din exemplul de împărţire a lor dat de tine?Eu cred că ar trebui să revezi cu atenţie secţiunea din matematică care tratează vectorii altfel se poate ajunge la greşeli nepermise care vor avea efecte nebănuite. 
Ce să mai vorbim de quaternioni şi de integrarea lor dacă nu se ştie ce sunt aceştia de fapt....
Ce să mai vorbim de quaternioni şi de integrarea lor dacă nu se ştie ce sunt aceştia de fapt....
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22205
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Da.
Pentru orice pozitie a vectorilor exemplul este bun
Vectorii sunt bine definiti.Impartirea lor nu este bine definita (am si precizat asta)
Prin ce este caracterizat un vector? Nu stii ?
Da o cautare pe google trebuie sa ai mare ghinion sa nu gasesti din prima o definitie la nivelul clasei a VII-a.
Pentru orice pozitie a vectorilor exemplul este bun
Vectorii sunt bine definiti.Impartirea lor nu este bine definita (am si precizat asta)
Prin ce este caracterizat un vector? Nu stii ?
Da o cautare pe google trebuie sa ai mare ghinion sa nu gasesti din prima o definitie la nivelul clasei a VII-a.
Vizitator- Vizitator
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Vei fi pedeplin multumit chiar mandru de definitia obtinuta.
Cat despre cvaternioni doar atat.Am cautat pe net ceva legat de integrarea lor,nu am gasit.Speram sa ma indrume cineva spre o idee un link ceva,nu s-a intamplat.Cvaternionii nu au nimic in comun cu fotbalul sau cu femeile deci se aplica principiul comun,daca nu stii este mai intelept sa taci.
In concluzie propun sa inchidem subiectul nerezolvat
Cat despre cvaternioni doar atat.Am cautat pe net ceva legat de integrarea lor,nu am gasit.Speram sa ma indrume cineva spre o idee un link ceva,nu s-a intamplat.Cvaternionii nu au nimic in comun cu fotbalul sau cu femeile deci se aplica principiul comun,daca nu stii este mai intelept sa taci.
In concluzie propun sa inchidem subiectul nerezolvat
Vizitator- Vizitator
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Corect!Eu am încercat să-i spun dar nu a înţeles şi în loc să tratăm cuaternionii am ajuns să discutăm despre vectori iar cuaternionii nu sunt vectori...... 
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22205
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Cuaternionii sunt o extensie a numerelor complexe iar geometric sunt reprezentate prin puncte intr-un sistem de 4 axe din care una este axa reala (de aceea se numesc cuaternioni pentru ai deosebi de numerele complexe şi eu le-aş zice cuaternionilor şi numere complexe spaţiale).Cuaternionul este deci un număr complex de forma  unde
unde  este partea reală ,
este partea reală ,  sunt părţile imaginare şi
sunt părţile imaginare şi  sau altfel spus din punct de vedere geometric cuaternionul este afixul punctului de coordonate
sau altfel spus din punct de vedere geometric cuaternionul este afixul punctului de coordonate }) .A nu se confunda afixul cu raza vectoare adică cu un vector deoarece afixul este de fapt capătul razei vectoare a punctului
.A nu se confunda afixul cu raza vectoare adică cu un vector deoarece afixul este de fapt capătul razei vectoare a punctului  iar raza vectoare are punctul de aplicaţie în originea sistemului celor 4 axe de coordonate.
iar raza vectoare are punctul de aplicaţie în originea sistemului celor 4 axe de coordonate.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22205
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Şi mai putem considera cuaternionul ca fiind un număr complex de numere complexe. Mai precis, deoarece avem relaţia k=ij, putem scrie un cuaternion ca fiind q=a+bi+cj+dij=(a+bi)+(c+di)j
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Poate că nu am înţeles eu bine ce este de fapt un cuaternion.Eu la facultatea din cadrul Politehnicii nu am învăţat despre cuaternioni.
Pentru ca să înţeleg ce este cuaternionul trebuie să ştiu ce sunt
trebuie să ştiu ce sunt  şi ce sunt
şi ce sunt  .Ce sunt
.Ce sunt  şi ce sunt
şi ce sunt  ?
?
Pentru ca să înţeleg ce este cuaternionul
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22205
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Convenim ca a, b, c şi d să fie numere reale, iar i, j şi k, unităţile imaginare. Încearcă şi articolul meu despre aceste unităţi. Te va ajuta să clarifici nişte chestiuni.
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Aşa am înţeles şi eu dar nu înţeleg de unde rezultă  dacă
dacă  sunt numerele imaginare astfel încât
sunt numerele imaginare astfel încât  .
. 
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22205
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Este consecinţa unui „produs generalizat” dintre doi cuaternioni, unul care să fie simultan produs scalar şi produs vectorial. Mai precis, produsul generalizat ne dă toate posibilităţile de înmulţire a elementelor bazei. Vezi pe Wikipedia.
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Am citit de mult acel link dar dacă este aşa tot nu pot înţelege de unde rezultă că produsul numerelor imaginare  şi
şi  este egal cu numărul imaginar
este egal cu numărul imaginar  .Trebuie să mă mai documentez.Care sunt valorile lui
.Trebuie să mă mai documentez.Care sunt valorile lui  ?
?
Ultima editare efectuata de catre Dacu in Joi 24 Ian 2013, 20:02, editata de 1 ori
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22205
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
i,j,k pot fi reprezentati prin matrici de ordinul 4
Si din produsul (anticomutativ) lor doua cate doua rezulta a treia matrice.
Mai pot fi reprezentate prin matrici complexe gamma (tot de ordinul patru)
Si din produsul (anticomutativ) lor doua cate doua rezulta a treia matrice.
Mai pot fi reprezentate prin matrici complexe gamma (tot de ordinul patru)
Vizitator- Vizitator
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Deci ce sunt  ?Sunt versori sau sunt numere imaginare sau sunt şi versori şi numere imaginare?Nu înţeleg!
?Sunt versori sau sunt numere imaginare sau sunt şi versori şi numere imaginare?Nu înţeleg! 
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22205
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Cvaternionii sunt numere hipercomplexe,a doua extensie a numerelor reale-ijk-sunt cvaternionii unitari.
Intra aici ca e super-bine explicat:
http://ro.wikipedia.org/wiki/Cuaternion
Intra aici ca e super-bine explicat:
http://ro.wikipedia.org/wiki/Cuaternion
Vizitator- Vizitator
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Şi acest link îl ştiu de mult dar nu înţeleg de unde rezultă că  ?Nu înţeleg!
?Nu înţeleg! 
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22205
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Integrarea cuaternionilor
Re: Integrarea cuaternionilor
Fa inmultirea matricilor de ordinul doi (ca este mai simplu) si vezi ca iese.
Asa a fost construit sa poti optine o norma pozitiv definita (reala)
Asa a fost construit sa poti optine o norma pozitiv definita (reala)
Vizitator- Vizitator
Pagina 2 din 2 •  1, 2
1, 2
Pagina 2 din 2
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum|
|
|




 Devino fan Forumgratuit
Devino fan Forumgratuit 