Sume interesante

Scris de **Syntax** Lun 29 Apr 2013, 17:12

Am intalnit proprietatea asta interesanta cautand sa definesc conceptul de infinit:
$\frac{1}{10}+\frac{1}{10^{2}}+\frac{1}{10^{3}}+...+\frac{1}{10^{n}}=0,(1)=\frac{1}{9}$
Pare o "contradictie", pentru ca adunand o infinitate de numere nenule ,pozitive nu-mi da infinit, ci un numar finit.
Acelasi lucru e valabil si pentru:
$\frac{n}{10}+\frac{n}{10^{2}}+...+\frac{n}{10^{n}}=\frac{n}{9}$

Scris de **Razvan** Lun 29 Apr 2013, 17:17

Syntax a scris:...adunand o infinitate de numere nenule ,pozitive nu-mi da infinit, ci un numar finit.

Nu aduni o infinitate de numere nenule, pozitive, ci n numere!

Scris de **Syntax** Lun 29 Apr 2013, 17:25

Razvan a scris:
Syntax a scris:...adunand o infinitate de numere nenule ,pozitive nu-mi da infinit, ci un numar finit.
Nu aduni o infinitate de numere nenule, pozitive, ci n numere!

Ideea este ca oricate numere adun doar cand n tinde la infinit, suma va fi 1/9.
In plus am observat ceva:
pentru n=9 rezulta 0,(9)=1 ceea ce nu e corect.
Trebuie sa refac calculele.Am gresit undeva.

Scris de **Syntax** Lun 29 Apr 2013, 17:39

O rectificare e necesara:
$\frac{k}{10}+\frac{k}{10^{2}}+...+\frac{k}{10^{n}}=\frac{k}{9}$

Pentru a nu se confunda n cu k.
Observ ca valorile lui k sunt limitate de la 1-8.

Scris de **Syntax** Lun 29 Apr 2013, 17:52

Cu exceptia lui k=9 relatia de mai sus este valabila pentru orice k, numar intreg pozitiv.
Desi se poate spune ca si 0,(9) la infinit este chiar 1.

Scris de Vizitator Lun 29 Apr 2013, 20:21

Syntax a scris:O rectificare e necesara:
$\frac{k}{10}+\frac{k}{10^{2}}+...+\frac{k}{10^{n}}=\frac{k}{9}$

Pentru a nu se confunda n cu k.
Observ ca valorile lui k sunt limitate de la 1-8.

Foloseste notatia asta daca l-ai trimis pe n la infinit
$\frac{k}{10}+\frac{k}{10^{2}}+\frac{k}{10^{3}}+...=\frac{k}{9}$

De ce ar fi limitate valorile lui k ?

Scris de **Syntax** Mar 30 Apr 2013, 10:26

$\frac{k}{10}+\frac{k}{10^{2}}+\frac{k}{10^{3}}+...+\frac{k}{10^{n}}+\frac{k}{10^{n+1}}+...=\frac{k}{9}$
Probabil asa este mai bine.
Se observa ca pentru k=9 se obtine egalitatea 0.(9)=1
Interesant este ca daca pentru k=1,2,3...10,11... suma de mai sus este valabila ( pentru n tinde la infinit ) pentru k=9 rezulta o "eroare" de 0,(0)1.
As interpreta astfel aceasta "eroare".
Suma numerelor respective este mai mica sau cel putin egala la infinit cu k/9.
Dar asta inseamna ca un numar este o suma "infinita" de numere!???
$1=\infty$

Scris de **Syntax** Mar 30 Apr 2013, 10:29

Pe scurt: La infinit toate numerele sunt egale.
Un fel de "relativitate" matematica.

Scris de Vizitator Mar 30 Apr 2013, 11:01

Syntax a scris: $\frac{k}{10}+\frac{k}{10^{2}}+\frac{k}{10^{3}}+...+\frac{k}{10^{n}}+\frac{k}{10^{n+1}}+...=\frac{k}{9}$
Probabil asa este mai bine.
Se observa ca pentru k=9 se obtine egalitatea 0.(9)=1
Interesant este ca daca pentru k=1,2,3...10,11... suma de mai sus este valabila ( pentru n tinde la infinit ) pentru k=9 rezulta o "eroare" de 0,(0)1.
As interpreta astfel aceasta "eroare".
Suma numerelor respective este mai mica sau cel putin egala la infinit cu k/9.
Dar asta inseamna ca un numar este o suma "infinita" de numere!???
$1=\infty$

Buna
Nu este nici o eroare,poate doar asa cu ghilimelele de rigoare
Suma ta de fapt este asta:
$k\left \{ \frac{1}{10}+\frac{1}{10^{2}}+\frac{1}{10^{3}}+...+\frac{1}{10^{n}} \right \} =k\frac{1}{10}\frac{\frac{1}{10}^{n}-1}{\frac{1}{10}-1}$
Este suma unei progresii geometrice de ratie 1/10
Daca il trimiti pe n la infinit nu faci alceva decat sa neglijezi termenul (1/10)^n exact eroarea pe care o aduci in discutie.

Da! Orice numar se poate scrie ca o si o suma infinita de numere (vezi dezvoltarea in serie Taylor a unei functii in jurul unui punct)
Exemple celebre sunt e si pi

$1=\infty$
Aici ai sarit peste cal.Una zici si alta scrii. Very Happy

Scris de **Syntax** Mar 30 Apr 2013, 12:08

Mezei Geza a scris:
$1=\infty$
Aici ai sarit peste cal.Una zici si alta scrii.

Exprimarea de mai sus nu e corecta , ai dreptate.
$1=\frac{9}{10}+\frac{9}{10^{2}}+\frac{9}{10^{3}}+...=0,(9)$
Si ca dezvoltarea seriei Taylor intr-un punct explica "eroarea" ai dreptate.

Scris de Vizitator Mar 30 Apr 2013, 12:25

Syntax a scris:
Mezei Geza a scris:
$1=\infty$
Aici ai sarit peste cal.Una zici si alta scrii.
Exprimarea de mai sus nu e corecta , ai dreptate.
$1=\frac{9}{10}+\frac{9}{10^{2}}+\frac{9}{10^{3}}+...=0,(9)$
Si ca dezvoltarea seriei Taylor intr-un punct explica "eroarea" ai dreptate.

Nu neaparat trebuie sa te complici cu o dezvoltare Taylor mult mai simplu poti sa observi asta din:
$9\left \{ \frac{1}{10}+\frac{1}{10^{2}}+\frac{1}{10^{3}}+...+\frac{1}{10^{n}} \right \} =9\frac{1}{10}\frac{\frac{1}{10}^{n}-1}{\frac{1}{10}-1}=9\frac{1}{9}\left ( 1-\frac{1}{10}^{n} \right )$
echivalent cu:
$\left \{ \frac{9}{10}+\frac{9}{10^{2}}+\frac{9}{10^{3}}+...+\frac{9}{10^{n}} \right \} =\left ( 1-\frac{1}{10}^{n} \right )$

Scris de **Syntax** Mar 30 Apr 2013, 13:00

Si Razvan a observat asta.
Cand adun n numere (un numar finit) totul e ok.
Dar pentru n infinit suma pentru k=9 va fi 0,999999 (infinit) si doar la infinit va fi 1.
Nu stiu cum sa exprim matematic decat cu semnul aproximativ egal.
Ar rezulta ca daca
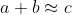
$a+b\approx c$
Atunci eroarea ar fi nedefinita, putand lua orice valori.

Scris de Vizitator Mar 30 Apr 2013, 13:20

Syntax a scris:Si Razvan a observat asta.
Cand adun n numere (un numar finit) totul e ok.
Dar pentru n infinit suma pentru k=9 va fi 0,999999 (infinit) si doar la infinit va fi 1.
Nu stiu cum sa exprim matematic decat cu semnul aproximativ egal.
Ar rezulta ca daca
$a+b\approx c$
Atunci eroarea ar fi nedefinita, putand lua orice valori.

Dupa parerea mea solutia este sa folosesti limite si ai rezolvat problema
$\lim_{n \to \infty }\left \{ \frac{9}{10}+\frac{9}{10^{2}}+\frac{9}{10^{3}}+...+\frac{9}{10^{n}} \right \}=1$
de fapt din aceasta cauza s-au si inventat

Scris de **meteor** Mar 30 Apr 2013, 22:57

Dupa parerea mea, sume cu adevarat interesante si misterioase sunt functiile zeta a lui Reimman, la moment (deoarece la acestea se stie precis valoarea sumei) in special petntru valori naturale pare.

Nu deaceea spun ca e misterios si interesant si nustiu ce, ca e la moda, ca sta miliionul, ci deoarece in joc la numitor se afla numerele naturale, valoarea sumei seriei pentru puteri naturale, este o valoare intregii sume e exprimata prin PI.
Aici minune.

Mare minune mai este pentru cazul cind exponentul terminilor este 1, in acest caz cica valoarea sumei tinde catre infinit.
Asa o divergenta, asa de greu sa creasca, eu nu am mai vazut, si nici nu imi inchipui cu poate fi, deoarece pentru valori a citevea zeci de mii, valoare sumei are valori foarte mici.

Scris de Vizitator Mar 30 Apr 2013, 23:28

meteor a scris:

Mare minune mai este pentru cazul cind exponentul terminilor este 1, in acest caz cica valoarea sumei tinde catre infinit.
Asa o divergenta, asa de greu sa creasca, eu nu am mai vazut, si nici nu imi inchipui cu poate fi, deoarece pentru valori a citevea zeci de mii, valoare sumei are valori foarte mici.

Cum adica "cica" Very Happy

?
Demonstratia divergentei este superba si foarte simpla.Intradevar creste "ciudat de incet" dar tot divergenta este !

Scris de **meteor** Joi 02 Mai 2013, 22:40

Mezei Geza a scris:
Cum adica "cica" ?

"cica"- adica cind auzi de la nea nu stiu cine, sau citesti undeva ceva, insa nu ai demonstratia pe masa.

Mezei Geza a scris:
Demonstratia divergentei este superba si foarte simpla.Intradevar creste "ciudat de incet" dar tot divergenta este !

Ce mai astepti, invitatie speciala expediata in plica la adresa ta postala?! Very Happy

Ada aici repede demonstratia aceea simpla de care spui.

Scris de Vizitator Joi 02 Mai 2013, 23:33

Da sefu"

Functia zeta pentru exponent unitar este:
$\zeta (1)=\sum_{n=1}^{\infty }\frac{1}{n}$
adica exact seria armonica.(sper sa nu fac vreo grava eroare)
Exista mai multe demonstratii ale divergentei acestei serii
Cea mai simpla demonstratie de fapt demonstratia care mi-a placut si la care m-am referit in postul de mai sus ( o dau si cu link ca am gasit-o intre timp )
http://en.wikipedia.org/wiki/Harmonic_series_%28mathematics%29
este demonstratia cand grupeaza termenii dupa puterile lui 2

Se scrie suma sub forma: 1+(1/2)+(1/3+1/4)+(1/5+1/6+1/7+1/8 )+(1/9+...1/16)+...
astfel incat in paranteze sa avem 2^0, 2^1, 2^2, 2^3,...2^n,... termeni
Din aceasta suma creaza o suma mai mica prin minorarea valorilor din paranteze la valoarea ultimului termen.
1+(1/2)+(1/4+1/4)+(1/8+1/8+1/8+1/8 )+(1/16+...1/16)+...
suma care se poate arata ca este egala cu:
1+1/2+2*(1/4)+4*(1/8 )+8*(1/16)+...=1+1/2+1/2+1/2+...1/2 ...
suma care va contine o infinitate de 1/2 deci este infinita.
Deci automat si seria armonica care este mai mare decat aceasta suma este tot infinita

Tot in acel link am gasit ca suma calculata pentru primii 10^43 termeni abia bate 100 !!

Sper ca nu am dat ceva de Terra !!

Scris de **meteor** Vin 03 Mai 2013, 00:14

ok, pina aici vad ca ti-ai indeplinit cerintele.

Intradevar e simpla demonstratia aceea (totus are parca inca ceva banal in ea).

Acum poti pleca la culcare, Very Happy

Scris de Vizitator Vin 03 Mai 2013, 00:22

Are ceva banal in ea ca doar nu degeaba este "banal de simpla" Very Happy

Am inteles! Am plecat! Very Happy

PS
Daca vrei o demonstratie mai "strong" ai acolo una cu integrala si aia este frumoasa

Scris de Continut sponsorizat

Sume interesante

Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante

Re: Sume interesante