O ecuație în mulțimea "C"

Scris de **Dacu** Dum 19 Apr 2020, 09:48

Să se rezolve ecuația $O ecuație în mulțimea "C" Gif$ unde $O ecuație în mulțimea "C" Gif$ și $O ecuație în mulțimea "C" Gif$ .

Scris de **virgil** Lun 20 Apr 2020, 13:18

Dacu a scris:Să se rezolve ecuația $O ecuație în mulțimea "C" Gif$ unde $O ecuație în mulțimea "C" Gif$ și $O ecuație în mulțimea "C" Gif$ .

Este vorba despre teorema lui Pitagora aplicata unui triunghi dreptunghic aflat in spatiul imaginar.

Scris de **Dacu** Lun 20 Apr 2020, 20:30

virgil a scris:
Dacu a scris:Să se rezolve ecuația $O ecuație în mulțimea "C" Gif$ unde $O ecuație în mulțimea "C" Gif$ și $O ecuație în mulțimea "C" Gif$ .
Este vorba despre teorema lui Pitagora aplicata unui triunghi dreptunghic aflat in spatiul imaginar.

Cum se calculează valorile lui a,b,c,d,e,f? Rolling Eyes

Scris de **CAdi** Lun 20 Apr 2020, 20:34

virgil a scris:
Dacu a scris:Să se rezolve ecuația $O ecuație în mulțimea "C" Gif$ unde $O ecuație în mulțimea "C" Gif$ și $O ecuație în mulțimea "C" Gif$ .
Este vorba despre teorema lui Pitagora aplicata unui triunghi dreptunghic aflat in spatiul imaginar.

Ai sesizat bine Virgil !
E bun si sahul Very Happy

Scris de **virgil** Lun 20 Apr 2020, 20:57

CAdi a scris:
virgil a scris:
Dacu a scris:Să se rezolve ecuația $O ecuație în mulțimea "C" Gif$ unde $O ecuație în mulțimea "C" Gif$ și $O ecuație în mulțimea "C" Gif$ .
Este vorba despre teorema lui Pitagora aplicata unui triunghi dreptunghic aflat in spatiul imaginar.

Ai sesizat bine Virgil !
E bun si sahul

E bun sahul, dar ma cam bate. Calculatorul este mai rapid si mai exact ca omul obisnuit. El cauta strategii de atac mult mai bune, fiind mai prevazator. Norocul meu este ca imi permite sa revin asupra mutarilor neinspirate de cate ori gresesc.

Scris de **CAdi** Lun 20 Apr 2020, 21:01

Da, dar iti imbunatateste atentia si sinapsele.
La ce nivel esti ? (La sah)

Scris de **virgil** Lun 20 Apr 2020, 21:29

CAdi a scris:
virgil a scris:
Dacu a scris:Să se rezolve ecuația $O ecuație în mulțimea "C" Gif$ unde $O ecuație în mulțimea "C" Gif$ și $O ecuație în mulțimea "C" Gif$ .
Este vorba despre teorema lui Pitagora aplicata unui triunghi dreptunghic aflat in spatiul imaginar.

Ai sesizat bine Virgil !
E bun si sahul

E bun sahul, dar ma cam bate. Calculatorul este mai rapid si mai exact ca omul obisnuit. El cauta strategii de atac mult mai bune, fiind mai prevazator. Norocul meu este ca imi permite sa revin asupra mutarilor neinspirate de cate ori gresesc.

Scris de **Dacu** Mar 21 Apr 2020, 08:26

CAdi a scris:
virgil a scris:
Dacu a scris:Să se rezolve ecuația $O ecuație în mulțimea "C" Gif$ unde $O ecuație în mulțimea "C" Gif$ și $O ecuație în mulțimea "C" Gif$ .
Este vorba despre teorema lui Pitagora aplicata unui triunghi dreptunghic aflat in spatiul imaginar.

Ai sesizat bine Virgil !
E bun si sahul

Nu cred că șahul poate ajuta pe cineva ca să rezolve ecuația propusă de mine!Tu ai auzit cumva de triunghi într-un spațiu imaginar? Rolling Eyes

Scris de **virgil** Mar 21 Apr 2020, 08:44

Dacu a scris:
CAdi a scris:
virgil a scris:
Este vorba despre teorema lui Pitagora aplicata unui triunghi dreptunghic aflat in spatiul imaginar.

Ai sesizat bine Virgil !
E bun si sahul
Nu cred că șahul poate ajuta pe cineva ca să rezolve ecuația propusă de mine!Tu ai auzit cumva de triunghi într-un spațiu imaginar?

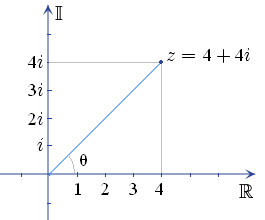
Multimea numerelor complexe reprezinta un spatiu imaginar, si poate fi reprezentat grafic, daca pe abscisa treci sirul numerelor reale, iar pe ordonata treci sirul numerelor imaginare. Avand trei puncte in acest spatiu, m-am gandit ca este vorba de un triunghi in spatiul imaginar. Asa m-a dus gandul la teorema lui Pitagora, fara sa mai fac vreun calcul. Daca tu stii sa rezolvi aceasta ecuatie cu sase necunoscute (a,b,c,d,e,f) te rog sa ne arati cum o faci. Ai in poza un exemplu de reprezentare a unui punct in spatiul imaginar.

Scris de **CAdi** Mar 21 Apr 2020, 11:16

Ar putea fi totusi niste solutii a necunoscutelor din spatiu imaginar cu corespondenta in spatiul real ;
De exemplu stim ca Teorema Lui Pitagora a^2+b^2=c^2 are una dintre solutii ca rezolvare in cadrul numerelor naturale :
a=3
b=4
c=5

Avem:
(a+bi)^2=3
(c+di)^2=4
(e+fi)^2=5
din ecuatia a doua c=1 si d=-1 celelalte va las pe voi sa le rezolvati...

Scris de **virgil** Mar 21 Apr 2020, 18:14

CAdi a scris:Ar putea fi totusi niste solutii a necunoscutelor din spatiu imaginar cu corespondenta in spatiul real ;
De exemplu stim ca Teorema Lui Pitagora a^2+b^2=c^2 are una dintre solutii ca rezolvare in cadrul numerelor naturale :
a=3
b=4
c=5

Avem:
(a+bi)^2=3
(c+di)^2=4
(e+fi)^2=5
din ecuatia a doua c=1 si d=-1 celelalte va las pe voi sa le rezolvati...

Trebuia sa-l lasi pe Dacu sa arate cum rezolva el problema celor sase necunoscute si o singura ecuatie.

Scris de **Dacu** Mier 22 Apr 2020, 09:04

virgil a scris:
Dacu a scris:
CAdi a scris:

Ai sesizat bine Virgil !
E bun si sahul
Nu cred că șahul poate ajuta pe cineva ca să rezolve ecuația propusă de mine!Tu ai auzit cumva de triunghi într-un spațiu imaginar?
Multimea numerelor complexe reprezinta un spatiu imaginar, si poate fi reprezentat grafic, daca pe abscisa treci sirul numerelor reale, iar pe ordonata treci sirul numerelor imaginare. Avand trei puncte in acest spatiu, m-am gandit ca este vorba de un triunghi in spatiul imaginar. Asa m-a dus gandul la teorema lui Pitagora, fara sa mai fac vreun calcul. Daca tu stii sa rezolvi aceasta ecuatie cu sase necunoscute (a,b,c,d,e,f) te rog sa ne arati cum o faci. Ai in poza un exemplu de reprezentare a unui punct in spatiul imaginar.

Eu nu am auzit de spațiu imaginar în matematicăCum definești tu spațiu imaginar?Am impresia că nu cunoști definiția numărului complex....Un număr complex este o pereche de numere reale ași b și se notează (a,b) sau z=a+bi unde "i" este numărul imaginar și pătratul numărului imaginar "i" este egal cu minus unu iar a este partea reală a numărului complex z și b este partea imaginară a aceluiaș numărului complex z....Mulțimea numerelor complexe se notează cu
$O ecuație în mulțimea "C" Gif$ .
Acea poză cu un așa zis exemplu de reprezentare a unui punct in spatiul imaginar este aberantă deoarece este greșit să notezi ordonatele cu "i" , "2i", "3i" etc. pe axa imaginară OIm și corect era să notezi ordonatele 1 , 2 , 3 etc. pe axa imaginară OIm și evident abscisele vor fi notate cu 1 , 2 , 3 etc. pe axa reală ORe și aceste două axe sunt ortogonale...Din acea poză rezultă de fapt că de fapt z=-12.... Rolling Eyes

Ar fi de râs dacă nu ar fi de plâns! Very Happy

De la Wikipedia citire despre Planul complex
"În matematică, planul complex sau planul z este o reprezentare geometrică a numerelor complexe într-un plan definit de axa reală și axa imaginară, ortogonale. El poate fi asemuit planului cartezian, cu reprezentarea părții reale a uni număr complex de-a lungul axei x, iar a părții imaginare de-a lungul axei y." și în acest sens citește https://ro.wikipedia.org/wiki/Planul_complex.
Teorema lui Pitagora privind triunghiul dreptunghic este una....dar este greșit să vorbești despre un triunghi dreptunghic "aflat în sapțiul imaginar".... Rolling Eyes

Din ecuația propusă de mine rezultă sistemul de ecuații:
$O ecuație în mulțimea "C" Gif$
Cum putem rezolva acest sistem de ecuații? Rolling Eyes

Scris de **virgil** Mier 22 Apr 2020, 10:33

Din moment ce ai o axa a numerelor reale si alta a numerelor imaginare, ambele formeaza un plan al numerelor complexe, care este un spatiu imaginar. Doar patratul acestor numere complexe dau numere reale.
Cea de a doua ecuatie nu ai postat-o de la inceput la deruta.

Scris de **CAdi** Mier 22 Apr 2020, 15:01

Dacu a scris:
Din ecuația propusă de mine rezultă sistemul de ecuații:
$O ecuație în mulțimea "C" Gif$
Cum putem rezolva acest sistem de ecuații?

Dacule prima ta ecuatie este gresita:
trebuie sa ai :
(a^2-b^2) +(c^2-d^2)=(e^2-f^2)+1
si
ab+cd =ef
si atunci avem urmatoarele solutii:

a^2-b^2=9 rezulta a=5 si b=4
c^2-d^2=16 rezulta c=5 si d=3
din :
ab+cd=ef avem 5*4+5*3=ef rezulta 20+15=ef deci ef =35
si rezulta e=7 si f=5
Solutiile verifica sistemul.

Scris de **Dacu** Mier 22 Apr 2020, 17:41

virgil a scris:Din moment ce ai o axa a numerelor reale si alta a numerelor imaginare, ambele formeaza un plan al numerelor complexe, care este un spatiu imaginar. Doar patratul acestor numere complexe dau numere reale.
Cea de a doua ecuatie nu ai postat-o de la inceput la deruta.

Afirmațiile tale privind așa zisul spațiu imaginar și pătratul numerelor complexe nu sunt corecte!În ce caz pătratul unui număr complex este un număr real? Rolling Eyes

Pătratul unui număr complex care are partea reală nenulă și partea imaginară nenulă este un număr complex care are partea reală nenulă și partea imaginară nenulă!Dacă "i" este numărul imaginar , atunci pătratul numărului "i" este egal cu minus 1. study

Despre care a doua ecuație vorbești tu? Rolling Eyes

Scris de **Dacu** Mier 22 Apr 2020, 18:21

CAdi a scris:
Dacu a scris:
Din ecuația propusă de mine rezultă sistemul de ecuații:
$O ecuație în mulțimea "C" Gif$
Cum putem rezolva acest sistem de ecuații?

Dacule prima ta ecuatie este gresita:
trebuie sa ai :
(a^2-b^2) +(c^2-d^2)=(e^2-f^2)+1
si
ab+cd =ef
si atunci avem urmatoarele solutii:

a^2-b^2=9 rezulta a=5 si b=4
c^2-d^2=16 rezulta c=5 si d=3
din :
ab+cd=ef avem 5*4+5*3=ef rezulta 20+15=ef deci ef =35
si rezulta e=7 si f=5
Solutiile verifica sistemul.

Ecuația ta , "(a^2-b^2) +(c^2-d^2)=(e^2-f^2)+1" din sistemul tău de ecuații , este greșită.Introdu valorile a,b,c,d,e,f găsite de tine în ecuația inițială propusă de mine spre rezolvare și vezi ce dă! Rolling Eyes

Am impresia că tu nu știi să calculezi pătratul unui număr complex....Cum calculezi tu $O ecuație în mulțimea "C" Gif$ ?
Refă calculele!!!!!!!!! study

Valorile a,b,c,d,e,f calculate de tine ar fi fost corecte doar dacă ecuația inițială cerută spre rezolvare ar fi fost $O ecuație în mulțimea "C" Gif$ .... Rolling Eyes

Scris de **CAdi** Mier 22 Apr 2020, 19:59

Ecuatia ta principala este gresita.Si felul cum ai pus problema.
Trebuie sa adaugi 1 daca vrei sa ai solutii. Altfel nu ai solutii..
Sistemul meu de ecuatii este cel corect.

Calculeaza sistemul tau de ecuatii si vezi ca nu-ti da nimic.

Scris de **Dacu** Joi 23 Apr 2020, 08:02

CAdi a scris:Ar putea fi totusi niste solutii a necunoscutelor din spatiu imaginar cu corespondenta in spatiul real ;
De exemplu stim ca Teorema Lui Pitagora a^2+b^2=c^2 are una dintre solutii ca rezolvare in cadrul numerelor naturale :
a=3
b=4
c=5

Avem:
(a+bi)^2=3
(c+di)^2=4
(e+fi)^2=5
din ecuatia a doua c=1 si d=-1 celelalte va las pe voi sa le rezolvati...

Valorile (a+bi)^2=3 , (c+di)^2=4 , (e+fi)^2=5 introduse în ecuația inițială propusă de mine spre rezolvare dau aberația 3+4=5...Ar fi de râs... Very Happy

dacă nu ar fi de plâns... Sad

Din (c+di)^2=4 dacă c=1 si d=-1 atunci rezultă că (1-i)^2=1-2i-1=-2i și astfel se ajunge la faptul că -2i=4 adică ar rezulta că numărul imaginar i=-2 ceea ce este aberant.... Rolling Eyes

Niciun număr complex de forma (c+di)^2 unde c și d sunt numere naturale nenule nu poate fi egal cu 4 și etc... Rolling Eyes

Mai cercetează! study

Scris de **Dacu** Joi 23 Apr 2020, 08:29

CAdi a scris:Ecuatia ta principala este gresita.Si felul cum ai pus problema.
Trebuie sa adaugi 1 daca vrei sa ai solutii. Altfel nu ai solutii..
Sistemul meu de ecuatii este cel corect.

Calculeaza sistemul tau de ecuatii si vezi ca nu-ti da nimic.

Nu trebuie adăugat 1! Rolling Eyes

Demonstrează ca ecuația ințială propusă de mine spre rezolvare nu are soluții!Iată , de exemplu , următoarele soluții pentru ecuația ințială propusă de mine spre rezolvare:
$O ecuație în mulțimea "C" Svg$ , $O ecuație în mulțimea "C" Svg$ și $O ecuație în mulțimea "C" Svg$ unde $O ecuație în mulțimea "C" Svg$ .
Cercetează corect și după aceea trage concluzii! Rolling Eyes

---------------------------------------
Dacă aș fi adăugat condiția ca numerele naturale nenule $O ecuație în mulțimea "C" Svg$ să fie prime între ele , atunci care ar fi soluțiile ecuației inițiale propusă de mine spre rezolvare? study

Scris de **CAdi** Joi 23 Apr 2020, 17:49

Foarte simplu!
a nu poate sa fie egal cu b ca ti-ar da 0 in prima ecuatie din sistem.
e nu poate fi egal f ca ar fi acelasi lucru 0
c cu d etc. Deci prima ta ecuatie ar fi "(a^2-b^2) +(c^2-d^2)=(e^2-f^2) =0
Afirmi numai absurditati.

Scris de **CAdi** Joi 23 Apr 2020, 18:00

Dacu a scris:
CAdi a scris:Ar putea fi totusi niste solutii a necunoscutelor din spatiu imaginar cu corespondenta in spatiul real ;
De exemplu stim ca Teorema Lui Pitagora a^2+b^2=c^2 are una dintre solutii ca rezolvare in cadrul numerelor naturale :
a=3
b=4
c=5

Avem:
(a+bi)^2=3
(c+di)^2=4
(e+fi)^2=5
din ecuatia a doua c=1 si d=-1 celelalte va las pe voi sa le rezolvati...
Valorile (a+bi)^2=3 , (c+di)^2=4 , (e+fi)^2=5 introduse în ecuația inițială propusă de mine spre rezolvare dau aberația 3+4=5...Ar fi de râs... dacă nu ar fi de plâns...
Din (c+di)^2=4 dacă c=1 si d=-1 atunci rezultă că (1-i)^2=1-2i-1=-2i și astfel se ajunge la faptul că -2i=4 adică ar rezulta că numărul imaginar i=-2 ceea ce este aberant....
Niciun număr complex de forma (c+di)^2 unde c și d sunt numere naturale nenule nu poate fi egal cu 4 și etc...
Mai cercetează!

Ai speculat o greseala de redactare :
e vorba de
(a+bi)^2=9
(c+di)^2=16
(e+fi)^2=25
cred ca esti de acord ca din ecuatia (a+bi)^2 +(c+di)^2=(e+fi)^2 rezulta 9+16=25

Pana una alta eu ti-am dat niste solutii la sistemul de ecuatii corectat.:
a=5,b=4,c=5,d=3,e=7,f=5

Scrie si tu solutiile la sistemul de ecuatii initial propus de tine ( fara 1) ,
de 2 ecuatii cu 6 necunoscute!
Ce valori ai gasit tu pentru a, b, c, d, si e ??

Scris de **Dacu** Vin 24 Apr 2020, 07:48

CAdi a scris:Foarte simplu!
a nu poate sa fie egal cu b ca ti-ar da 0 in prima ecuatie din sistem.
e nu poate fi egal f ca ar fi acelasi lucru 0
c cu d etc. Deci prima ta ecuatie ar fi "(a^2-b^2) +(c^2-d^2)=(e^2-f^2) =0
Afirmi numai absurditati.

Am înțeles de ce nu înțelegi ceea ce îți spun....S-ar putea ca numele tău de utilizator "CAdi" să-l fi ales pentru că te consideri practicant al așa zisei religiei creștin-ortodoxe iar a cădi înseamnă a tămâia numai că tămâia și tămâierea ta nu este de bună calitate în ceea ce privește rezolvarea problemei propusă de mine dar eu tind să cred că numele tău de utilizator fiind "CAdi" vine de fapt de la cuvântul turcesc "Kadi" care înseamnă judecător musulman cu atribuții civile și religioase.... Rolling Eyes

Ești cumva turc și de aceea nu înțelegi ceea ce spun?!? Rolling Eyes

Repet problema:

Să se rezolve ecuația $O ecuație în mulțimea "C" Gif$ unde $O ecuație în mulțimea "C" Gif$ și $O ecuație în mulțimea "C" Gif$ .

Unde scrie în problema propusă de mine că am impus restricția că numarul a nu poate fi egal cu numărul b , că numarul c nu poate fi egal cu numărul d și că numarul e nu poate fi egal cu numărul f.
Numerele $O ecuație în mulțimea "C" Svg$ , $O ecuație în mulțimea "C" Svg$ și $O ecuație în mulțimea "C" Svg$ unde $O ecuație în mulțimea "C" Svg$ date de mine verifică foarte bine sistemul de ecuații

$O ecuație în mulțimea "C" Gif$

care rezultă din ecuația inițială din problema propusă de mine spre rezolvare...
Ce fel de cercetare faci tu , dacă nu poți înțelege ceea ce spun?!?Tu ai propus o altă problemă cu adăugatul numărului 1 la ecuația inițială fără nicio logică....
Deocamdată nici eu nu știu să rezolv sistemul de ecuații

$O ecuație în mulțimea "C" Gif$ ....

altfel de cum am dat acele soluții.... Sad

Voi mai cerceta! study

Dacă aș impune restricția suplimentară ca numerele a , b , c , d , e , f să fie prime între ele , atunci este evident că nu se mai poate ca a=b , c= d , e=f și deci ecuația inițiala ar fi mai greu de rezolvat sau ar fi mai greu de demonstrat că în acest caz de restricție ecuația inițiala propusă de mine spre rezolvare nu are soluții în mulțimea numerelor naturale nenule... Rolling Eyes

Poate că acum vei înțelege ceea ce spun...iar dacă nu mai cercetează și vino cu idei concrete la ceea ce am propus și nu mai fă afirmații aberante... study

Scris de **virgil** Vin 24 Apr 2020, 08:22

Dacu tu din capul locului ai postat o ecuatie cu 6 necunoscute. punct.
Aceasta ecuatie nu poate avea a=b, c=d, e=f, pentru ca nu poti scrie acelasi necunoscuta cu doua simboluri diferite. In cazul numerelor complexe cand a=b, atunci (a+ib)^2=a2+2aib - b2 = > inlocuind pe b=a rezulta ca a2 se simplifica cu -b2, si rezulta (a+ib)^2=2ia2 ; adica partea reala este zero, ramanand numai partea imaginara a numarului complex 2.i.a^2 ;
La fel si cu celelalte paranteze, si in final obtii ; 2ia2+ 2ic2=2ie2 , adica o suma de doua numere imaginare ia2+ic2=ie2 ; Asta poate avea o infinitate de solutii situate pe axa numerelor imaginare.
Pentru ca sa nu dispara componenta reala a acestor numere complexe trebuiau inlocuite cu conjugatele lor.

Scris de **Dacu** Vin 24 Apr 2020, 08:45

virgil a scris:Dacu tu din capul locului ai postat o ecuatie cu 6 necunoscute. punct.
Aceasta ecuatie nu poate avea a=b, c=d, e=f, pentru ca nu poti scrie acelasi necunoscuta cu doua simboluri diferite. Umbli cu aiureli ca sa testezi vigilenta altora.

Problema propusă de mine este foarte corectă deoarece eu inițial nu am resticționat faptul că a nu poate fi egal cu b , că c nu poate fi egal cu d....Este aiuritor când văd asemenea aberații spuse în domeniul matematicii pe cest forum....Ar fi de râs Very Happy

dacă nu ar fi de plâns Sad

...Habar nu ai de matematică dar te bagi unde nu te pricepi și îi dai cu presupusul....Am să pun problema propusă de mine pe un alt forum să vedem ce spun cei de acolo! Rolling Eyes

Aș fi foarte curios să aflu părerea unui matematician...ca de exemplu și părerea lui Abel Cavași care a făcut facultatea de matematică... Rolling Eyes

Scris de **virgil** Vin 24 Apr 2020, 09:07

virgil a scris:Dacu tu din capul locului ai postat o ecuatie cu 6 necunoscute. punct.
Aceasta ecuatie nu poate avea a=b, c=d, e=f, pentru ca nu poti scrie acelasi necunoscuta cu doua simboluri diferite. In cazul numerelor complexe cand a=b, atunci (a+ib)^2=a2+2aib - b2 = > inlocuind pe b=a rezulta ca a2 se simplifica cu -b2, si rezulta (a+ib)^2=2ia2 ; adica partea reala este zero, ramanand numai partea imaginara a numarului complex 2.i.a^2 ;
La fel si cu celelalte paranteze, si in final obtii ; 2ia2+ 2ic2=2ie2 , adica o suma de doua numere imaginare ia2+ic2=ie2 ; Asta poate avea o infinitate de solutii situate pe axa numerelor imaginare.
Pentru ca sa nu dispara componenta reala a acestor numere complexe trebuiau inlocuite cu conjugatele lor.

Scris de **Dacu** Vin 24 Apr 2020, 10:28

virgil a scris:Dacu tu din capul locului ai postat o ecuatie cu 6 necunoscute. punct.
Aceasta ecuatie nu poate avea a=b, c=d, e=f, pentru ca nu poti scrie acelasi necunoscuta cu doua simboluri diferite. In cazul numerelor complexe cand a=b, atunci (a+ib)^2=a2+2aib - b2 = > inlocuind pe b=a rezulta ca a2 se simplifica cu -b2, si rezulta (a+ib)^2=2ia2 ; adica partea reala este zero, ramanand numai partea imaginara a numarului complex 2.i.a^2 ;
La fel si cu celelalte paranteze, si in final obtii ; 2ia2+ 2ic2=2ie2 , adica o suma de doua numere imaginare ia2+ic2=ie2 ; Asta poate avea o infinitate de solutii situate pe axa numerelor imaginare.
Pentru ca sa nu dispara componenta reala a acestor numere complexe trebuiau inlocuite cu conjugatele lor.

Pentru ca să-ți dai seama cât de greșit este ceea ce spui , eu aș vrea ca să-mi răspunzi la următoarele întrebări:
1) Care este graficul funcției $O ecuație în mulțimea "C" Gif$ unde $O ecuație în mulțimea "C" Gif$ ?
2) Care este graficul funcției $O ecuație în mulțimea "C" Gif$ ?
3) Ce vrei să spui cu afirmația ta "Pentru ca sa nu dispara componenta reala a acestor numere complexe trebuiau inlocuite cu conjugatele lor."?Detaliază? Rolling Eyes

Scris de **Abel Cavaşi** Vin 24 Apr 2020, 10:44

Dacu a scris:Aș fi foarte curios să aflu părerea unui matematician...ca de exemplu și părerea lui Abel Cavași care a făcut facultatea de matematică...

Dacă ești curios să afli părerea mea, poți fi liniștit că îți dau dreptate, problema este frumoasă și corectă și are soluții în mulțimea numerelor naturale.

Unde nu îți dau dreptate este comportamentul aberant față de cei care greșesc. Ce urmărești, să demonstrezi că toți suntem proști și tu ești deșteptul? Vrei să dovedești cumva că forumul e plin de proști? Pe care fraier o să-l poți convinge de asta? Trebuie să fii tu însuți tare tutuluc ca să crezi că un om prost și-ar pierde vremea pe un forum liniștit care dorește binele umanității, prin încercările sale modeste de a contribui cumva la progresul Științei.

Și te rog să consideri intervenția mea drept un avertisment față de atacul la persoană pe care îl practici necontenit. Dai cumva dovadă de prea mare deșteptăciune? Te rog să ai grijă la astfel de vorbe:

Dacu a scris:Am înțeles de ce nu înțelegi ceea ce îți spun....S-ar putea ca numele tău de utilizator "CAdi" să-l fi ales pentru că te consideri practicant al așa zisei religiei creștin-ortodoxe iar a cădi înseamnă a tămâia numai că tămâia și tămâierea ta nu este de bună calitate în ceea ce privește rezolvarea problemei propusă de mine dar eu tind să cred că numele tău de utilizator fiind "CAdi" vine de fapt de la cuvântul turcesc "Kadi" care înseamnă judecător musulman cu atribuții civile și religioase.... Ești cumva turc și de aceea nu înțelegi ceea ce spun?!?

Scris de **Dacu** Vin 24 Apr 2020, 12:55

CAdi a scris:
Dacu a scris:
CAdi a scris:Ar putea fi totusi niste solutii a necunoscutelor din spatiu imaginar cu corespondenta in spatiul real ;
De exemplu stim ca Teorema Lui Pitagora a^2+b^2=c^2 are una dintre solutii ca rezolvare in cadrul numerelor naturale :
a=3
b=4
c=5

Avem:
(a+bi)^2=3
(c+di)^2=4
(e+fi)^2=5
din ecuatia a doua c=1 si d=-1 celelalte va las pe voi sa le rezolvati...
Valorile (a+bi)^2=3 , (c+di)^2=4 , (e+fi)^2=5 introduse în ecuația inițială propusă de mine spre rezolvare dau aberația 3+4=5...Ar fi de râs... dacă nu ar fi de plâns...
Din (c+di)^2=4 dacă c=1 si d=-1 atunci rezultă că (1-i)^2=1-2i-1=-2i și astfel se ajunge la faptul că -2i=4 adică ar rezulta că numărul imaginar i=-2 ceea ce este aberant....
Niciun număr complex de forma (c+di)^2 unde c și d sunt numere naturale nenule nu poate fi egal cu 4 și etc...
Mai cercetează!
Ai speculat o greseala de redactare :
e vorba de
(a+bi)^2=9
(c+di)^2=16
(e+fi)^2=25
cred ca esti de acord ca din ecuatia (a+bi)^2 +(c+di)^2=(e+fi)^2 rezulta 9+16=25

Pana una alta eu ti-am dat niste solutii la sistemul de ecuatii corectat.:
a=5,b=4,c=5,d=3,e=7,f=5

Scrie si tu solutiile la sistemul de ecuatii initial propus de tine ( fara 1) ,
de 2 ecuatii cu 6 necunoscute!
Ce valori ai gasit tu pentru a, b, c, d, si e ??

Altă greșeală faci!Ce pot să mai zic ca să pricepi ce spun...?!?...De exemplu din propunerea ta (a+bi)^2=9 rezultă că a=3 și b=0 iar b=0 încalcă condiția din problema propusă de mine că numerele a , b , c , d , e , f trebuie să fie numere naturale nenule.... Rolling Eyes

Scris de **Dacu** Vin 24 Apr 2020, 13:32

Abel Cavaşi a scris:
Dacu a scris:Aș fi foarte curios să aflu părerea unui matematician...ca de exemplu și părerea lui Abel Cavași care a făcut facultatea de matematică...
Dacă ești curios să afli părerea mea, poți fi liniștit că îți dau dreptate, problema este frumoasă și corectă și are soluții în mulțimea numerelor naturale.

Unde nu îți dau dreptate este comportamentul aberant față de cei care greșesc. Ce urmărești, să demonstrezi că toți suntem proști și tu ești deșteptul? Vrei să dovedești cumva că forumul e plin de proști? Pe care fraier o să-l poți convinge de asta? Trebuie să fii tu însuți tare tutuluc ca să crezi că un om prost și-ar pierde vremea pe un forum liniștit care dorește binele umanității, prin încercările sale modeste de a contribui cumva la progresul Științei.

Și te rog să consideri intervenția mea drept un avertisment față de atacul la persoană pe care îl practici necontenit. Dai cumva dovadă de prea mare deșteptăciune? Te rog să ai grijă la astfel de vorbe:

Dacu a scris:Am înțeles de ce nu înțelegi ceea ce îți spun....S-ar putea ca numele tău de utilizator "CAdi" să-l fi ales pentru că te consideri practicant al așa zisei religiei creștin-ortodoxe iar a cădi înseamnă a tămâia numai că tămâia și tămâierea ta nu este de bună calitate în ceea ce privește rezolvarea problemei propusă de mine dar eu tind să cred că numele tău de utilizator fiind "CAdi" vine de fapt de la cuvântul turcesc "Kadi" care înseamnă judecător musulman cu atribuții civile și religioase.... Ești cumva turc și de aceea nu înțelegi ceea ce spun?!?

Mulțumesc foarte mult pentru aprecierile făcute de tine privind problema propusă de mine! flower

Nu prea cred că "virgil" și/sau "CAdi" nu vor continua să spună în continuare tot felul de aberații privind problema propusă de mine.... Rolling Eyes

Hai să vorbim românește căci văd că folosești diacritice ceea ce este corect pentru că altfel putem înțelege altceva.... Rolling Eyes

Ai comis un atac la persoană dacă crezi că eu sunt tutuluc , deaorece tutuluc înseamnă prostănac! study

Poate că ai vrut să spui că eu sunt mai cu țuțuluc adică sunt mai cu moț... Rolling Eyes

Nu mă consider mai cu moț adică mai iscusit ca alții dar nici chiar așa să văd că după ce unii greșesc nici măcar nu vor să recunoască că ei greșesc și nici să vrea să-și ceră scuze....a șe vedea aberațiile matematice și nu numai spuse de marele moderator "virgil" și de bietul "CAdi" care nu e în stare ca un adept al așa zisei religii creștin-ortodoxe să ceară în public să-i iert greșelile pe care le face în domeniul matematicii și nu numai în acest domeniu...
Când cineva nu înțelege ceva , i se spune "Ești turc , ce nu-nțelegi?"."Ești turc , ce nu înțelegi?" este de fapt o expresie românească și deci nu este un atac la persoană.... Rolling Eyes

Dacă îi spuneam lui "CAdi" că este prost sau că este tutuluc , atunci da , acest fapt ar fi fost un atac la persoană.... Rolling Eyes

Scris de **Abel Cavaşi** Vin 24 Apr 2020, 14:37

Dacu a scris:Ai comis un atac la persoană dacă crezi că eu sunt tutuluc , deaorece tutuluc înseamnă prostănac!

Nicăieri n-am spus că ești un tutuluc, ci am spus că tutuluceala ta ar fi o consecință logică ce poate fi dedusă din comportamentul tău aberant pe acest forum.

Nu mă consider mai cu moț adică mai iscusit ca alții dar nici chiar așa să văd că după ce unii greșesc nici măcar nu vor să recunoască că ei greșesc și nici să vrea să-și ceră scuze...

Trăiești cu speranțe deșarte, dacă vrei ca oamenii obișnuiți să recunoască faptul că au greșit și apoi să-și mai și ceară scuze când greșesc. Prea mari pretenții de unde nu sunt. Aruncă la gunoi asemenea speranțe și mergi mai departe în „suferință”. Altfel spus, „tacă-ți fleanca și scrie numai despre cercetare”.

Când cineva nu înțelege ceva , i se spune "Ești turc , ce nu-nțelegi?"."Ești turc , ce nu înțelegi?" este de fapt o expresie românească și deci nu este un atac la persoană.... Dacă îi spuneam lui "CAdi" că este prost sau că este tutuluc , atunci da , acest fapt ar fi fost un atac la persoană....

Acuma n-o să fac aici filozofia tutulucului sau a turcului. Oricum o iei, tot atac la persoană este, oricât de subtil ar fi vrut să fie. Pe scurt, CEL CARE A ÎNCEPUT este vinovatul. Așa că, data viitoare NU MAI ÎNCEPE atacuri la persoană.

Scris de Continut sponsorizat

O ecuație în mulțimea "C"

O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"

Re: O ecuație în mulțimea "C"