Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Forever_Man Astazi la 18:21
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la No_name în Ce anume "generează" legile fizice?
( 1 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 1 )
» Mesaj de la Abel Cavaşi în Daci nemuritori
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12458) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Dacu2 | ||||
| Forever_Man | ||||
| Abel Cavaşi | ||||
| Meteorr |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| Dacu2 | ||||
| virgil | ||||
| CAdi | ||||
| Meteorr | ||||
| ilasus | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 49 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 49 Vizitatori Nici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Factorialul
Pagina 1 din 1
 Factorialul
Factorialul
Conjectura: Daca scrim un sir de numere naturale termenii caruia sunt ridicati la o putere naturala k, terminii celui de al doilea sir, fiind sub primul sir, ei fiind diferenta dintre termenii confecutivi ai primului sir, repetind procedeul, vom ajunge ca termenii ultimului sir sunt totii egali intre ei, ei fiind egali cu 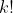 , ca in imagine:
, ca in imagine:
^{k} & (n+2)^{k} & (n+3)^{k} & ... & \\ 2^{k}-1^{k}& 3^{k}-2^{k} & 4^{k}-3^{k} &... & (n+1)^{k}-n^{k} & ... & ... & ...& ...\\ ....&......&.....&.....&.....&......&.....&....&....\\ k!&k! &k! &k! &k! &k! &k! &k! &... & \end{matrix})
Deci vom avea:
^{i}C^{i}_{k}(k-i+1)^{k},\forall k\geq 0)
sau
^{i}C^{i}_{k}(n-i+1)^{k},\forall n\geq k\geq 0) .
.
Cine se apuca de demonstrat trebue sa demonstreze ca scaderea succesiva a terminilor ridicati la putere, va da un numar ce reprezinta factorialul puterii, sau sa demonstreze direct acea egalitate.
Poate, acea egalitate va putea ajuta la calculul direct al factorialului.
Deci vom avea:
sau
Cine se apuca de demonstrat trebue sa demonstreze ca scaderea succesiva a terminilor ridicati la putere, va da un numar ce reprezinta factorialul puterii, sau sa demonstreze direct acea egalitate.
Poate, acea egalitate va putea ajuta la calculul direct al factorialului.
Ultima editare efectuata de catre meteor in Sam 16 Feb 2013, 23:31, editata de 1 ori
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Factorialul
Re: Factorialul
omuldinluna a scris:Dacă te interesează să faci de mână un n! fără să fie nevoie să faci toate înmulțirile, uită-te aici:
http://en.wikipedia.org/wiki/Gamma_function
G(n+1)=n!
deci dacă ți se pare mai ușor să faci integrala decât toate înmulțirile, problema ar fi deja rezolvată. Numai să ai răbdare să integrezi prin părți.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Factorialul
Re: Factorialul
Vom modifica putin notatiile care le-am facut, caci suntem deprinsi a lucra putin cu alte notatii.meteor a scris:Conjectura: Daca scrim un sir de numere naturale termenii caruia sunt ridicati la o putere naturala k, terminii celui de al doilea sir, fiind sub primul sir, ei fiind diferenta dintre termenii confecutivi ai primului sir, repetind procedeul, vom ajunge ca termenii ultimului sir sunt totii egali intre ei, ei fiind egali cu, ca in imagine:
Deci vom avea:
sau.
Cine se apuca de demonstrat trebue sa demonstreze ca scaderea succesiva a terminilor ridicati la putere, va da un numar ce reprezinta factorialul puterii, sau sa demonstreze direct acea egalitate.
Poate, acea egalitate va putea ajuta la calculul direct al factorialului.
Deaceea propun asa sa fie:
Ca sa nu o facem pe desteptul, nu vad ce necesitate ar avea la moment sa aplicam a doua formula, deaceea pina cind nu vom avea mare nevoe de a doua formula, nu ne atingem de ea, ca numai ne complicam.
Deci vom "incerca" sa rezolvam prima formula:
Aceasta am facut pentru a scapa de
Acum avem batae de cap cu
Analizind triunghiul lui Pascal, vom abserva ca toate combinarile din x luate cite i se obtin recursiv.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Factorialul
Re: Factorialul
Analizind triunghiul lui Pascal observam ca:
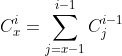 ,unde
,unde 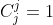 .
.
Aici se observa recursivitatea de obtinere a combinarilor de grad superior.
Deci cautam in continuare o modatitate de exprimare a combinarilor NU in functie de combinari si sau in functie de factorial.
Chinezeasca noastra [cu mici corectii] devine:
[la noua egalitate posibil sa fi scapat ceva erori]
^{i}C^{i}_{x}(x-i+1)^{x}=\sum_{i=0}^{2x}C_{2x}^{i}(2x-i+1)^{2x}-\left ( \sum_{i=0}^{2x+1}C_{2x+1}^{i}(2x-i+2)^{2x+1}\right )=\sum_{i=0}^{2x} \sum_{j=2x-1}^{i-1} C_{j}^{i-1}(j-i)^{j}-\left ( \sum_{i=0}^{2x+1}\sum_{j=2x}^{i-1}C_{j}^{i-1}(j-i)^{j}\right ) ,\forall x\geq 0) ,unde
,unde 
[Ce e drept, aici se lucreaza la reinventarea bicicletei cu o roata si jumatate. Bicicletele cu alte roti [cam tot felul de biciclete] demult timp au fost inventate deja de sfinti ca: Euler, Gauss, etc. ]
Aici se observa recursivitatea de obtinere a combinarilor de grad superior.
Deci cautam in continuare o modatitate de exprimare a combinarilor NU in functie de combinari si sau in functie de factorial.
Chinezeasca noastra [cu mici corectii] devine:
[la noua egalitate posibil sa fi scapat ceva erori]
[Ce e drept, aici se lucreaza la reinventarea bicicletei cu o roata si jumatate. Bicicletele cu alte roti [cam tot felul de biciclete] demult timp au fost inventate deja de sfinti ca: Euler, Gauss, etc. ]
Ultima editare efectuata de catre meteor in Mar 19 Feb 2013, 12:19, editata de 1 ori
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Factorialul
Re: Factorialul
Spre exemplu din formula:
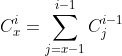
Incercam sa vedem ce se intimpla pentru anumite cazuri particulare.
0.
1.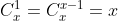
2.(x-2)}{2})
3.(j-2)}{2}=\frac{1}{2}\sum_{j=x-1}^{2}\left ( j^{2} -3j+2\right )=\frac{1}{2}\sum_{j=x-1}^{2}j^{2}-\frac{3}{2}\sum_{j=x-1}^{2}j+1)
Mai departe stim cum se calculeaza sumele patratice si simple.
etc.
Se observa caci la fiecare grad cu care ne ridicam in sus, avem nevoe de formula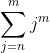 , insa aceasta formula in ziua de azi se calculeaza relatii care la fel sunt exprimate fie prin factoriale, fie prin combinari.
, insa aceasta formula in ziua de azi se calculeaza relatii care la fel sunt exprimate fie prin factoriale, fie prin combinari.
Deci, pina la moment am facut - nimic.
Incercam sa vedem ce se intimpla pentru anumite cazuri particulare.
0.
1.
2.
3.
Mai departe stim cum se calculeaza sumele patratice si simple.
etc.
Se observa caci la fiecare grad cu care ne ridicam in sus, avem nevoe de formula
Deci, pina la moment am facut - nimic.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 