Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Meteorr Ieri la 21:34
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Joi 21 Noi 2024, 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la virgil în NEWTON
( 1 )
» Mesaj de la Meteorr în Global warming is happening?
( 1 )
» Mesaj de la eugen în În ce tip de dovezi aveţi încredere deplină?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Dacu2 | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Abel Cavaşi |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| virgil | ||||
| Dacu2 | ||||
| Meteorr | ||||
| ilasus | ||||
| CAdi | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 21 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 21 Vizitatori :: 2 Motoare de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Întrebări-răspunsuri din matematică
2 participanți
Pagina 1 din 1
 Întrebări-răspunsuri din matematică
Întrebări-răspunsuri din matematică
1. Cum demonstrăm că există c, d, astfel încât orice număr mai mic sau egal cu (a+b) poate fi exprimat ca ac-bd ?
a,b,c,d naturale, nenule.
2. Cum demonstrăm că nu există a, b naturale, nenule, diferite, astfel încât (a^n)-(b^n) se divide cu produsul ab ?
3. Cum demonstrăm că dacă a-b se divide cu c-d, atunci atât ac-bd se divide cu c-d, cât și ad-bc se divide cu c-d ?
a,b,c,d naturale, nenule.
4. Cum demonstrăm că dacă a+b se divide cu c-d, atunci atât ac+bd se divide cu c-d, cât și ad+bc se divide cu c-d ?
a,b,c,d naturale, nenule.
a,b,c,d naturale, nenule.
2. Cum demonstrăm că nu există a, b naturale, nenule, diferite, astfel încât (a^n)-(b^n) se divide cu produsul ab ?
3. Cum demonstrăm că dacă a-b se divide cu c-d, atunci atât ac-bd se divide cu c-d, cât și ad-bc se divide cu c-d ?
a,b,c,d naturale, nenule.
4. Cum demonstrăm că dacă a+b se divide cu c-d, atunci atât ac+bd se divide cu c-d, cât și ad+bc se divide cu c-d ?
a,b,c,d naturale, nenule.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
curiosul a scris:
4. Cum demonstrăm că dacă a+b se divide cu c-d, atunci atât ac+bd se divide cu c-d, cât și ad+bc se divide cu c-d ?
a,b,c,d naturale, nenule.
daca a+b se divide cu c-d rezulta a+b=u(c-d) si rezulta:a=uc-ud-b
In aceste conditii:
ad+bc=(uc-ud-b)d+bc=
ucd-udd-bd+bc=ud(c-d)-b(c-d)=(ud-b)(c-d)
similar:
ac+bd =(uc-ud-b)c+bd=
ucc-udc-bc+bd=uc(c-d)-b(c-d)=(uc-b)(c-d)
ambele se divid cu c-d
La punctul trei se face similar
Vizitator- Vizitator
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
La 2 o ideecuriosul a scris:
2. Cum demonstrăm că nu există a, b naturale, nenule, diferite, astfel încât (a^n)-(b^n) se divide cu produsul ab ?
1. Cum demonstrăm că există c, d, astfel încât orice număr mai mic sau egal cu (a+b) poate fi exprimat ca ac-bd ?
a,b,c,d naturale, nenule.
1-Fa exact cum am facut eu mai demult folosind polinoamele
a=x
b=b
2-sau fa dezvoltarea (a-b)(a^(n-1)+...)
a-b sigur nu se divide deoarece 1/b-1/a mai mic ca 1
din a doua paranteza termenii care nu se divid cu ab sunt primul si ultimul:(a^n-1)-(b^n-1)
eventual prin recurenta poti obtine ceva
1- Nu imi este clar ce vrei sa demonstrezi si nici din ce am inteles nu am idee cum ar trebuii inceputa
Vizitator- Vizitator
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
La intrebarea a doua :Mezei Geza a scris:La 2 o ideecuriosul a scris:
2. Cum demonstrăm că nu există a, b naturale, nenule, diferite, astfel încât (a^n)-(b^n) se divide cu produsul ab ?
1. Cum demonstrăm că există c, d, astfel încât orice număr mai mic sau egal cu (a+b) poate fi exprimat ca ac-bd ?
a,b,c,d naturale, nenule.
1-Fa exact cum am facut eu mai demult folosind polinoamele
a=x
b=b
2-sau fa dezvoltarea (a-b)(a^(n-1)+...)
a-b sigur nu se divide deoarece 1/b-1/a mai mic ca 1
din a doua paranteza termenii care nu se divid cu ab sunt primul si ultimul:(a^n-1)-(b^n-1)
eventual prin recurenta poti obtine ceva
1- Nu imi este clar ce vrei sa demonstrezi si nici din ce am inteles nu am idee cum ar trebuii inceputa
Pentru a, b, n naturale, nenule, diferite folosind dezvoltarea (a-b)(a^(n-1)+...) se poate demonstra elegant prin inductie ca afirmatia este corecta.Posibil se poate demonstra acelasi lucru si pentru: (a^n)+(b^n)
Daca nu te descurci scrie si te ajut.
Vizitator- Vizitator
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Salut Geza și bine-ai revenit !
Frumos demonstrat pentru 3 și 4. Exact așa le-am demonstrat și eu.
Pentru 2, nu m-am gândit la asta, dar sunt sigur că ai dreptate și se poate și prin recurență.
Eu am abordat o altă modalitate, pe care, din păcate, nu am timp acum s-o detaliez.
La punctul 1.
Să presupunem că a=15 și b=49, suma lor este 64.
Orice număr mai mic decât 64 se poate scrie sub forma (15*c)-(49*d) ?
Sau există c și d astfel încât orice număr mai mic ca 64 să se poată scrie (15*c)-(49*d) ?
Ideea este că dacă a și b sunt ambele pare, indiferent cu ce numere le-am înmulți, diferența acestor produse va fi un număr par.
Iar pentru că vorbim de orice număr mai mic ca a+b, mai menționăm că a și b nu sunt ambele numere pare.
Frumos demonstrat pentru 3 și 4. Exact așa le-am demonstrat și eu.
Pentru 2, nu m-am gândit la asta, dar sunt sigur că ai dreptate și se poate și prin recurență.
Eu am abordat o altă modalitate, pe care, din păcate, nu am timp acum s-o detaliez.
La punctul 1.
Să presupunem că a=15 și b=49, suma lor este 64.
Orice număr mai mic decât 64 se poate scrie sub forma (15*c)-(49*d) ?
Sau există c și d astfel încât orice număr mai mic ca 64 să se poată scrie (15*c)-(49*d) ?
Ideea este că dacă a și b sunt ambele pare, indiferent cu ce numere le-am înmulți, diferența acestor produse va fi un număr par.
Iar pentru că vorbim de orice număr mai mic ca a+b, mai menționăm că a și b nu sunt ambele numere pare.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Bine te-am gasit !
Sa inteleg ca si la punctul 1 ai reusit sa gasesti demonstratia ?
Daca da nu imi mai bat capul cu ea !
Sa inteleg ca si la punctul 1 ai reusit sa gasesti demonstratia ?
Daca da nu imi mai bat capul cu ea !
Vizitator- Vizitator
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Nu tocmai !Mezei Geza a scris:Bine te-am gasit !
Sa inteleg ca si la punctul 1 ai reusit sa gasesti demonstratia ?
Daca da nu imi mai bat capul cu ea !
Am verificat doar prin calcule și am schițat câteva condiții.
Dar o găsesc eu și pe aia completă.
Ideea pentru care am deschis topicul este că nu am găsit aceste observații pe nicăieri, deși sunt simple și pot fi frumos demonstrate.
Eventual pot fi utile și folosite.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Și totuși Geza, pentru 1 și 2 mai trebui menționate câteva aspecte, ca afirmațiile să fie adevărate :
Altfel, dacă a și b au un divizor comun, diferența ac-bd se va divide cu acel divizor indiferent de c și d (nenule).
Și nu orice număr mai mic ca a+b se divide cu divizorul comun al lui a și b.
Deci a și b prime între ele.
2. Cu excepția situației în care a este o putere de b. Dacă a este b^x, atunci pentru orice n strict mai mare ca x, a^n-b^n se divide cu ab.
Cazul 4^3-2^3=64-8=56=7*8
Și este valabil pentru oricare alt caz pentru care a este o putere de b.
Corect ?
1. Ca afirmația să fie adevărată este necesară condiția a și b prime între ele.curiosul a scris:1. Cum demonstrăm că există c, d, astfel încât orice număr mai mic sau egal cu (a+b) poate fi exprimat ca ac-bd ?
a,b,c,d naturale, nenule.
2. Cum demonstrăm că nu există a, b naturale, nenule, diferite, astfel încât (a^n)-(b^n) se divide cu produsul ab ?
Altfel, dacă a și b au un divizor comun, diferența ac-bd se va divide cu acel divizor indiferent de c și d (nenule).
Și nu orice număr mai mic ca a+b se divide cu divizorul comun al lui a și b.
Deci a și b prime între ele.
2. Cu excepția situației în care a este o putere de b. Dacă a este b^x, atunci pentru orice n strict mai mare ca x, a^n-b^n se divide cu ab.
Cazul 4^3-2^3=64-8=56=7*8
Și este valabil pentru oricare alt caz pentru care a este o putere de b.
Corect ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Corect si inca !curiosul a scris:Și totuși Geza, pentru 1 și 2 mai trebui menționate câteva aspecte, ca afirmațiile să fie adevărate :2. Cu excepția situației în care a este o putere de b. Dacă a este b^x, atunci pentru orice n strict mai mare ca x, a^n-b^n se divide cu ab.curiosul a scris:1. Cum demonstrăm că există c, d, astfel încât orice număr mai mic sau egal cu (a+b) poate fi exprimat ca ac-bd ?
a,b,c,d naturale, nenule.
2. Cum demonstrăm că nu există a, b naturale, nenule, diferite, astfel încât (a^n)-(b^n) se divide cu produsul ab ?
Cazul 4^3-2^3=64-8=56=7*8
Și este valabil pentru oricare alt caz pentru care a este o putere de b.
Corect ?
La doi are exceptii,si nu numai cazul in care unul este o putere a celuilalt,exceptii sunt si in anumite cazuri cand numerele sunt multiplii ale aceleasi puteri.
de exemplu:
(8,4) ,n=3 (2^3,2^2) notam x=3, y=2
8^3-4^3=512-64=448=14*8*4
de exemplu:
(8,4) ,n=2 (2^3,2^2) x=3,y=2
8^2-4^2=64-16=48=3*8*2 nu se divide cu 8*4
aceste exceptii sunt si functie de valoarea lui x,y,n.
Trebuie facute calculele riguros ,cel putin cum am gandit-o eu asa in cap aceste exceptii se "vad" cat de cat
Vizitator- Vizitator
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Exact Geza !Mezei Geza a scris:
Corect si inca !
La doi are exceptii,si nu numai cazul in care unul este o putere a celuilalt,exceptii sunt si in anumite cazuri cand numerele sunt multiplii ale aceleasi puteri.
Cu alte cuvinte, enunțul 2 este o regulă demonstrabilă, dacă și doar dacă, a și b au cel puțin un factor prim diferit.
O primă aplicație a enunțului 1, adică dacă a și b sunt numere prime între ele, atunci orice număr mai mic ca a+b poate fi scris ca ac-bd, o putem folosi pentru abordarea într-un mod diferit a ecuației teoremei lui Fermat :
Am tot socotit astăzi, dar nu am ajuns la ceva satisfăcător.
M-am folosit și de faptul că x+y-z trebuie să se dividă cu p, în cazul n=p prim impar.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
[quote="curiosul"]
Exact Geza !
Cu alte cuvinte, enunțul 2 este o regulă demonstrabilă, dacă și doar dacă, a și b au cel puțin un factor prim diferit.
Dacă și doar dacă nu este prea corect formulat.
Am vrut să spun ceva de genul, dacă a și b nu au cel puțin un factor prim diferit, atunci există un n, pentru care a^n-b^n se divide cu produsul ab.
Aș mai avea o întrebare Geza.
Fie a-b se divide cu p prim.
Există vreo relație generalizată, cu excepția cazurilor triviale, între valorile c și d, astfel încât și ac-bd se divide cu p ?
Pentru moment aș spune că este necesară și suficientă condiția ca și c-d să fie divizibil cu p, prin cazurile 3 și 4 pe care le-ai demonstrat deja.
Exact Geza !
Cu alte cuvinte, enunțul 2 este o regulă demonstrabilă, dacă și doar dacă, a și b au cel puțin un factor prim diferit.
Dacă și doar dacă nu este prea corect formulat.
Am vrut să spun ceva de genul, dacă a și b nu au cel puțin un factor prim diferit, atunci există un n, pentru care a^n-b^n se divide cu produsul ab.
Aș mai avea o întrebare Geza.
Fie a-b se divide cu p prim.
Există vreo relație generalizată, cu excepția cazurilor triviale, între valorile c și d, astfel încât și ac-bd se divide cu p ?
Pentru moment aș spune că este necesară și suficientă condiția ca și c-d să fie divizibil cu p, prin cazurile 3 și 4 pe care le-ai demonstrat deja.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
O prima corectiecuriosul a scris:curiosul a scris:
Fie a-b se divide cu p prim.
Există vreo relație generalizată, cu excepția cazurilor triviale, între valorile c și d, astfel încât și ac-bd se divide cu p ?
Pentru moment aș spune că este necesară și suficientă condiția ca și c-d să fie divizibil cu p, prin cazurile 3 și 4 pe care le-ai demonstrat deja.
c+d divizibil cu p -parca asa trebuie sa rezulte pentru ac-bd
Da este o conditie suficienta dar posibil sa ai si alte solutii
Ma gandesc si revin cu o solutie
Vizitator- Vizitator
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Cred ca este exact cum zici,dar putem si demonstra similar cum am facut la 3 si 4curiosul a scris:curiosul a scris:
Fie a-b se divide cu p prim.
Există vreo relație generalizată, cu excepția cazurilor triviale, între valorile c și d, astfel încât și ac-bd se divide cu p ?
Pentru moment aș spune că este necesară și suficientă condiția ca și c-d să fie divizibil cu p, prin cazurile 3 și 4 pe care le-ai demonstrat deja.
Daca a-b se divide cu p inseamna a-b=p*k de unde rezulta:
a=b+p*k sau
b=a-p*k
In aceste conditii ac-bd=(b+p*k)c-(a-p*k)d=-(ad-bc)+p*k(c+d)
Rezulta ca pentru ca ac-bd se se divida cu p oricare ar fi c si d o conditie mult mai larga ar putea fi ca (ad-bc) se se divida cu a-b deoarece a-b=p*k
????????????????????????????????
Ceva asemanator am aratat la pct 3 si 4,deja incep sa ma incurc in semne :)Vezi daca este corect pana aici
Vizitator- Vizitator
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
OK.
Dezvoltând în continuare egalitatea la care ai ajuns (corectă, de altfel) :
Simplificând prin c+d ajungem exact la ipoteza problemei.
Deci se pare că în acest fel nu am avansat prea tare.
Oricum, mulțumesc pentru interes.
A apărut ceva mai interesant.
Se pare că putem aduce demonstrarea inexistenței soluțiilor întregi ale ecuației x^n+y^n=z^n, pentru n mai mare ca 2, doar la a arăta că ecuația x^n+y^n=(y+1)^n nu are soluții întregi pentru n mai mare ca 2.
Și asta plecând de la x^n+y^n=(ax-by)^n.
Pentru că aducem egalitatea la forma x^n=(ax-by)^n-y^n, pe care de asemenea, o putem aduce la forma x^n=[ax-y(b+1)]*{...}.
Situație în care ax-y(b+1) nu poate avea alți factori primi diferiți de cei ai lui x. Pentru că paranteza pătrată și acolada pot avea doar p factor comun (pentru n=p prim impar), iar y și x sunt prime între ele (deci b+1 ar conține factorul lui x, sau s-ar divide cu x), rezultă că dacă x nu se divide cu p, atunci din paranteza pătrată nu poate fi scos factorul lui x la puterea p, caz în care rămâne valabilă situația în care ax-y(b+1)=1, deci ax-by=y+1, de asemenea z=y+1.
Și s-ar reduce la a arăta că x^p+y^p=(y+1)^p.
Desigur, sunt mult mai multe detalii care trebuie explicate și trebuie demonstrații pentru faptul că dacă x și y sunt prime între ele, atunci orice număr mai mic ca x+y se poate scrie ca ax-by, și pentru faptul că dacă n este mai mare ca 2, atunci ecuația x^p+y^p=(y+1)^p nu are soluții întregi.
Pentru prima parte, trebuie arătat că nu există sx-ty=1, pentru ca dacă a=y+rs, iar b=x+rt, atunci ax-by=(y+rs)x-(x+rt)y=r(sx-ty).
Dacă există s,t, astfel încât pentru x, y, prime între ele sx-ty=1, există r, adică r poate avea orice valoare astfel încât orice număr mai mic ca x+y să poată fi scris ca ax-by.
Desigur poate tu ajungi la o demonstrație mai simplă.
Când o să am ceva mai mult timp liber, o să-ți scriu cât de detaliat consider necesar să-ți explic cum consider că rezultă ce am scris mai sus.
Mi-aș dori măcar o părere din partea ta.
Dezvoltând în continuare egalitatea la care ai ajuns (corectă, de altfel) :
ajungem la (a-b)(c+d)=p*k(c+d), trecând în stânga -(ad-bc).Mezei Geza a scris:ac-bd=(b+p*k)c-(a-p*k)d=-(ad-bc)+p*k(c+d)
Simplificând prin c+d ajungem exact la ipoteza problemei.
Deci se pare că în acest fel nu am avansat prea tare.
Oricum, mulțumesc pentru interes.
A apărut ceva mai interesant.
Se pare că putem aduce demonstrarea inexistenței soluțiilor întregi ale ecuației x^n+y^n=z^n, pentru n mai mare ca 2, doar la a arăta că ecuația x^n+y^n=(y+1)^n nu are soluții întregi pentru n mai mare ca 2.
Și asta plecând de la x^n+y^n=(ax-by)^n.
Pentru că aducem egalitatea la forma x^n=(ax-by)^n-y^n, pe care de asemenea, o putem aduce la forma x^n=[ax-y(b+1)]*{...}.
Situație în care ax-y(b+1) nu poate avea alți factori primi diferiți de cei ai lui x. Pentru că paranteza pătrată și acolada pot avea doar p factor comun (pentru n=p prim impar), iar y și x sunt prime între ele (deci b+1 ar conține factorul lui x, sau s-ar divide cu x), rezultă că dacă x nu se divide cu p, atunci din paranteza pătrată nu poate fi scos factorul lui x la puterea p, caz în care rămâne valabilă situația în care ax-y(b+1)=1, deci ax-by=y+1, de asemenea z=y+1.
Și s-ar reduce la a arăta că x^p+y^p=(y+1)^p.
Desigur, sunt mult mai multe detalii care trebuie explicate și trebuie demonstrații pentru faptul că dacă x și y sunt prime între ele, atunci orice număr mai mic ca x+y se poate scrie ca ax-by, și pentru faptul că dacă n este mai mare ca 2, atunci ecuația x^p+y^p=(y+1)^p nu are soluții întregi.
Pentru prima parte, trebuie arătat că nu există sx-ty=1, pentru ca dacă a=y+rs, iar b=x+rt, atunci ax-by=(y+rs)x-(x+rt)y=r(sx-ty).
Dacă există s,t, astfel încât pentru x, y, prime între ele sx-ty=1, există r, adică r poate avea orice valoare astfel încât orice număr mai mic ca x+y să poată fi scris ca ax-by.
Desigur poate tu ajungi la o demonstrație mai simplă.
Când o să am ceva mai mult timp liber, o să-ți scriu cât de detaliat consider necesar să-ți explic cum consider că rezultă ce am scris mai sus.
Mi-aș dori măcar o părere din partea ta.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Fără nusubliniat mai sus. Există s,t astfel încât sx-ty=1 pentru x, y prime între ele.curiosul a scris:Pentru prima parte, trebuie arătat că nu există sx-ty=1, pentru ca dacă a=y+rs, iar b=x+rt, atunci ax-by=(y+rs)x-(x+rt)y=r(sx-ty).
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
M-ai incuiat din prima 
Ar fi bine sa fi sigur de asta:
"Se pare că putem aduce demonstrarea inexistenței soluțiilor întregi ale ecuației x^n+y^n=z^n, pentru n mai mare ca 2, doar la a arăta că ecuația x^n+y^n=(y+1)^n nu are soluții întregi pentru n mai mare ca 2."
si mai apoi sa dezvolti.
Ar fi bine sa fi sigur de asta:
"Se pare că putem aduce demonstrarea inexistenței soluțiilor întregi ale ecuației x^n+y^n=z^n, pentru n mai mare ca 2, doar la a arăta că ecuația x^n+y^n=(y+1)^n nu are soluții întregi pentru n mai mare ca 2."
si mai apoi sa dezvolti.
Vizitator- Vizitator
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Ok, sunt convins că nu se înțelege mare lucru, mesajul a fost scris la repezeală pentru că nu aveam timp.
Să le luăm șa rând.
Dacă x și y sunt prime între ele, iar ax-y(b+1) conține în factorizarea lui doar factori primi pe care-i are și x, rezultă obligatoriu că b+1 trebuie să-i conțină de asemenea, atât timp cât y nu-i poate conține deoarece x și y sunt prime între ele.
Înainte de a continua, cred că este destul de important să observăm vreo relație între a,x,b,y atât timp cât ax-by este mai mic decât x+y. Pare a fi destul de dificil să generalizăm ceva. Eu cel puțin, n-am reușit deocamdată și cred că m-ar ajuta mult.
Revenim la ax-y(b+1).
Acesta rezultă scriind z^n-y^n=(z-y)(...).
Dacă z este ax-by, atunci z-y este ax-by-y=ax-y(b+1).
Din ecuația x^n=z^n-y^n=(z-y)(...) rezultă că x^n=[ax-y(b+1)](...).
Egalitatea de mai sus nu este posibilă dacă ax-y(b+1) are vreun factor prim pe care nu-l are x.
Plecam de la acest aspect și încercăm să analizăm dacă există a și b astfel încât ax-y(b+1) să nu aibă alți factori primi față de ce-i pe care-i are x, cu x și y prime între ele. Se pare că nu prea există.
Dar trebuie riguros demonstrat, eu doar am încercat să văd ce iese din calcule numerice și în toate cazurile pe care le-am încercat ax-y(b+1) are și alți factori primi, diferiți de ce-i ai lui x, dacă x și y sunt prime între ele.
Dar există a și b astfel încât ax-y(b+1)=1, cu x și y prime între ele, pentru că ecuația ar putea admite soluții z și y cu z-y=1.
Asta înseamnă că ax-by-y=1, ax-by=y+1, deci soluția z=y+1, plecând de la notația z=ax-by.
În acest fel ar trebui să găsim soluțiile ecuației x^n+y^n=(y+1)^n.
Se pare că și așa pare totuși destul de complicat.
Oricum, în mare cam asta este linia logică, dar...trebuiesc foarte multe detalii demonstrate.
Nu știu dacă se poate fructifica ceva de pe aici, dar merită analizat.
Dacă reușesc să demonstrez vreun detaliu te anunț, iar până una alta, m-ai putea ajuta să vedem cum stă treaba cu scrierea unui număr mai mic ca x+y, ca fiind ax-by.
Să le luăm șa rând.
Dacă x și y sunt prime între ele, iar ax-y(b+1) conține în factorizarea lui doar factori primi pe care-i are și x, rezultă obligatoriu că b+1 trebuie să-i conțină de asemenea, atât timp cât y nu-i poate conține deoarece x și y sunt prime între ele.
Înainte de a continua, cred că este destul de important să observăm vreo relație între a,x,b,y atât timp cât ax-by este mai mic decât x+y. Pare a fi destul de dificil să generalizăm ceva. Eu cel puțin, n-am reușit deocamdată și cred că m-ar ajuta mult.
Revenim la ax-y(b+1).
Acesta rezultă scriind z^n-y^n=(z-y)(...).
Dacă z este ax-by, atunci z-y este ax-by-y=ax-y(b+1).
Din ecuația x^n=z^n-y^n=(z-y)(...) rezultă că x^n=[ax-y(b+1)](...).
Egalitatea de mai sus nu este posibilă dacă ax-y(b+1) are vreun factor prim pe care nu-l are x.
Plecam de la acest aspect și încercăm să analizăm dacă există a și b astfel încât ax-y(b+1) să nu aibă alți factori primi față de ce-i pe care-i are x, cu x și y prime între ele. Se pare că nu prea există.
Dar trebuie riguros demonstrat, eu doar am încercat să văd ce iese din calcule numerice și în toate cazurile pe care le-am încercat ax-y(b+1) are și alți factori primi, diferiți de ce-i ai lui x, dacă x și y sunt prime între ele.
Dar există a și b astfel încât ax-y(b+1)=1, cu x și y prime între ele, pentru că ecuația ar putea admite soluții z și y cu z-y=1.
Asta înseamnă că ax-by-y=1, ax-by=y+1, deci soluția z=y+1, plecând de la notația z=ax-by.
În acest fel ar trebui să găsim soluțiile ecuației x^n+y^n=(y+1)^n.
Se pare că și așa pare totuși destul de complicat.
Oricum, în mare cam asta este linia logică, dar...trebuiesc foarte multe detalii demonstrate.
Nu știu dacă se poate fructifica ceva de pe aici, dar merită analizat.
Dacă reușesc să demonstrez vreun detaliu te anunț, iar până una alta, m-ai putea ajuta să vedem cum stă treaba cu scrierea unui număr mai mic ca x+y, ca fiind ax-by.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Și mai am o nedumerire.
Fie z mai mic ca x+y, pe care-l putem scrie
z=ax - by = (a_1)x - (b_1)y = (a_2)x - (b_2)y = ...=(a_m)x - (b_m)y=...
Dacă în tot acest șir există a_m și b_m pentru care diferența (a_m)x - [(b_m)+1]y conține un factor prim pe care nu-l conține x, putem să alegem aceste a_m și b_m pentru a exprima soluția z ?
a_m - a indice m.
Fie z mai mic ca x+y, pe care-l putem scrie
z=ax - by = (a_1)x - (b_1)y = (a_2)x - (b_2)y = ...=(a_m)x - (b_m)y=...
Dacă în tot acest șir există a_m și b_m pentru care diferența (a_m)x - [(b_m)+1]y conține un factor prim pe care nu-l conține x, putem să alegem aceste a_m și b_m pentru a exprima soluția z ?
a_m - a indice m.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Geza,
cum am putea demonstra că pentru a și b prime între ele, unul par și unul impar,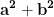 și a+b nu pot avea niciun factor comun ?
și a+b nu pot avea niciun factor comun ?
Desigur, întrebarea este adresată oricăruia dintre voi, dar l-am menționat pe Geza pentru că a fost singurul care și-a spus părerea la acest tip de întrebări pe care le-am ridicat în ultimul timp.
cum am putea demonstra că pentru a și b prime între ele, unul par și unul impar,
Desigur, întrebarea este adresată oricăruia dintre voi, dar l-am menționat pe Geza pentru că a fost singurul care și-a spus părerea la acest tip de întrebări pe care le-am ridicat în ultimul timp.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Ultima editare efectuata de catre meteor in Lun 07 Oct 2013, 21:14, editata de 1 ori (Motiv : Nu, e gresit, deoarece ambele ar iesi ca sunt pare)
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Hai sa ne gandim un pic cu voce tarecuriosul a scris:Geza,
cum am putea demonstra că pentru a și b prime între ele, unul par și unul impar,și a+b nu pot avea niciun factor comun ?
Desigur, întrebarea este adresată oricăruia dintre voi, dar l-am menționat pe Geza pentru că a fost singurul care și-a spus părerea la acest tip de întrebări pe care le-am ridicat în ultimul timp.
Daca cele doua expresii ar avea un factor comun as putea scrie:
unde k este un numar intreg.
Egalitate echivalenta cu :
Dar:
dar a+b este numar intreg si conditia ca k sa fie numar intreg s-ar rezuma ca si :
Dar daca unul este par si unul impar (a+b) este sigur impar,si ab respectiv 2ab este par
rezulta ca raportul respectiv este (2*impar*par)/impar
Vezi! Dar nu cred ca te ajuta cu prea mult.
O luam de la capat
Vizitator- Vizitator
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
respectiv:
a-b respectiv b-a sunt numere intregi,problema se rezuma la a gasi care este conditia ca ultimul termen din cele doua egalitati sa fie un numar intreg.
Notam a+b=c
Fie a=a1*a2*a3...an respectiv b=b1*b2*b3..bn descompunerea in factori primi a lui a respectiv al lui b
Cu aceste notatii ultimul termen din cele doua egalitati se rescrie sub forma:
respectiv:
aceste rapoarte sunt egale cu un numar intreg daca c se regaseste intre factorii primi al lui a (din prima egalitate) si intre factori primi al lui b (din a doua egalitate) Fapt ce este in contradictie cu ipoteza unde am presupus ca a si b nu au factori primi comuni.
Deasemenea tot din ipoteza avem a sau b unul par respectiv celalalt impar de unde rezulta c impar (de fapt era suficienta conditia c diferit de 1 sau 2)si nu se poate simplifica cu 2-ul din rapoartele obtinute.
In concluzie a^2+b^2 si a+b nu pot avea un factor comun intreg in conditiile date in ipoteza.
Singura exceptie de la aceasta regula este cazul banal a+b=+-1
Sper ca este corect si te ajuta cu ceva.
Vizitator- Vizitator
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Mulțumesc Geza !
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Ecuația 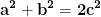 are alte soluții cu excepția soluțiilor
are alte soluții cu excepția soluțiilor 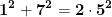 ?
?
Dacă da, pot fi generalizate soluțiile întregi ale acestei ecuații după o anumită exprimare generală a lor ?
Dacă da, pot fi generalizate soluțiile întregi ale acestei ecuații după o anumită exprimare generală a lor ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
Eu presimt ca mai sunt solutii,de generalizat e foarte greu ( o singura egalitate,trei necunoscute-tare maestru trebuie sa fi sa poti obtine ceva)curiosul a scris:Ecuațiaare alte soluții cu excepția soluțiilor
?
Dacă da, pot fi generalizate soluțiile întregi ale acestei ecuații după o anumită exprimare generală a lor ?
Sa incerc o tentativa la prima intrebare.
Presupunem ca a,b,c sunt solutii
Daca la egalitatea obtinuta mai sus atat in numarator cat si in numitor adunam un x sau un X^2 egalitatea nu se schimba.Rezulta:
Acuma nu imi ramane decat sa formez patrate perfecte din careva termen patratic plus x sau x^2 din numarator si respectiv din numitor.
Hai sa incercam cu c^2 si X^2 ca este mai putin de scris desi poate este mai greu.
In concluzie:
Si trebuie sa demonstrez ca exista c,x,v,u cu proprietatea de mai sus
Observ ca aceste sunt numere pitagorice si stiu ca exista o relatie calculata pentru numerele pitagorice care o sa incerc sa o aplic
Daca
atunci
Pentru c=5 pana aici este f frumos dar deloc util.
Deoarece x-ul gasit nu mai da un patrat perfect si in a doua egalitate.Vezi poate la multipli de 5 da ceva.
Vezi pana aici si mai completeaza cu o idee doua .Trebuie reluata eventual pentru cazul X si nu X^2
E deja tarziu ma retrag.
Tu nu ai PM ?
Cand mai postezi cate ceva si crezi ca te pot ajuta trimite un mesaj ,eu o sa intru mai rar in urmatoarea perioada.
Vizitator- Vizitator
 Re: Întrebări-răspunsuri din matematică
Re: Întrebări-răspunsuri din matematică
OK, mersi Geza.
Întrebarea a apărut analizând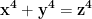 și aducând egalitatea la forma unei ecuații pitagorice
și aducând egalitatea la forma unei ecuații pitagorice 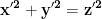 , unde
, unde 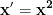 ,
,  ,
,  cu soluțiile
cu soluțiile
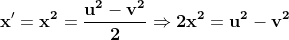
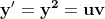
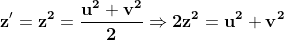
cu u, v impare prime între ele.
O să analizez mai bine ideile tale să vedem dacă putem fructifica ceva.
Dacă da, îți trimit un PM.
Întrebarea anterioară la care mi-ai răspuns și tu și meteor, era pentru a demonstra că dacă x, y, z sunt toate prime între ele, cu x par, atunci}) și
și }) îl au pe 2 singurul lor factor comun.
îl au pe 2 singurul lor factor comun.
Mulțumesc pentru răspuns.
Întrebarea a apărut analizând
cu u, v impare prime între ele.
O să analizez mai bine ideile tale să vedem dacă putem fructifica ceva.
Dacă da, îți trimit un PM.
Întrebarea anterioară la care mi-ai răspuns și tu și meteor, era pentru a demonstra că dacă x, y, z sunt toate prime între ele, cu x par, atunci
Mulțumesc pentru răspuns.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 