Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Forever_Man Astazi la 18:21
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la eugen în Ce fel de popor suntem
( 1 )
» Mesaj de la CAdi în OZN in Romania
( 1 )
» Mesaj de la virgil în Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12458) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Dacu2 | ||||
| Forever_Man | ||||
| Abel Cavaşi | ||||
| Meteorr |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| Dacu2 | ||||
| virgil | ||||
| CAdi | ||||
| Meteorr | ||||
| ilasus | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 32 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 32 Vizitatori Nici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
O ecuaţie uşor de rezolvat.....
3 participanți
Pagina 1 din 1
 O ecuaţie uşor de rezolvat.....
O ecuaţie uşor de rezolvat.....
Să se rezolve ecuaţia  unde
unde  .
. 


Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Ia zi maestre, cum o rezolvi în întregi pozitivi mai întâi.
Care sunt soluțiile ?
Dacă e o demonstrație frumoasă, îți dau eu un premiu.
Dar trebuie să demonstrezi că dacă toate soluțiile sunt mai mari ca 1, ecuația are sau nu soluții x, y, z prime între ele.
Cred că ai încercat tu ceva, dar cred că ai și vreo greșeală pe acolo.
Care sunt soluțiile ?
Dacă e o demonstrație frumoasă, îți dau eu un premiu.
Dar trebuie să demonstrezi că dacă toate soluțiile sunt mai mari ca 1, ecuația are sau nu soluții x, y, z prime între ele.
Cred că ai încercat tu ceva, dar cred că ai și vreo greșeală pe acolo.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Ai dreptate, e ușor de rezolvatDacu a scris:Să se rezolve ecuaţiaunde
.



Dar trebuie să demonstrezi că dacă x, y, z sunt toate mai mari ca 1, ecuația are soluții doar dacă x, y, z au toate un factor comun.
Sau nu.
Mă îndoiesc că poți să demonstrezi ușor asta.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Hai Dacule nu ma lasa in intuneric !Dacu a scris:Să se rezolve ecuaţiaunde
.



Ma predau ! Nu o stiu rezolva !
Prezinta demonstratia sa nu mai pierdem vremea.
Vizitator- Vizitator
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Iar ecuația are și soluții prime între ele, pentru că se ajunge la triplete pitagoreice, toate pare, unde x+y și x-y sunt pare.
Una dintre soluții este
Dacu are dreptate, se rezolvă simplu.
Ideea este a unui utilizator de pe forumul din lincul pe care l-am dat în celălalt subiect.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Da.M-am uitat si eu intre timp.curiosul a scris:
Iar ecuația are și soluții prime între ele, pentru că se ajunge la triplete pitagoreice, toate pare, unde x+y și x-y sunt pare.
Una dintre soluții este
Dacu are dreptate, se rezolvă simplu.
Ideea este a unui utilizator de pe forumul din lincul pe care l-am dat în celălalt subiect.
Cu cei de acolo ar trebui tu sa iei legatura.Aveti pasiuni comune.
Cum stai cu engleza?
Vizitator- Vizitator
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Nici prea prea, nici foarte foarte.Mezei Geza a scris:Da.M-am uitat si eu intre timp.
Cu cei de acolo ar trebui tu sa iei legatura.Aveti pasiuni comune.
Cum stai cu engleza?
Mai sunt cuvinte pe care nu le știu, dar de multe ori le deduc sensul din contextul frazei.
Am fost odată la niște cursuri în Finlanda care s-au ținut în engleză și pentru care ulterior am tradus câteva manuale de utilizare a unor aparate de radiologie maxilo-facială din engleză în română.
M-aș descurca.
Dar cred că sunt cam mic pentru ei și cred că e suficient că vă enervez și vă stresez pe voi.
Cel puțin, voi v-ați obișnuit cu mine.
În cazul acestei ecuații, verific acum dacă nu cumva are soluții primitive doar dacă
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Rezolvarea evidentă este următoarea.Dacu a scris:Să se rezolve ecuaţiaunde
.
În primul rând, x și y nu pot avea paritate diferită, pentru că
Deci x și y au aceeași paritate.
În continuare, ajungem la
undecuriosul a scris:
Pentru că x și y au aceeași paritate, soluțiile de mai sus sunt triplete pitagoreice întregi, toate prime între ele dacă x și y sunt prime între ele.
Dar observăm că
de unde rezultă că ecuația inițială trebuie să fie una de forma
cu
Acestea sunt soluțiile.
Alegând u, v prime între ele, obținem toate soluțiile primitive ale ecuației.
Celelalte derivă din acestea.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Fără supărare ,dar raţionamentul tău este incomplet........
Care sunt formulele de găsire a numerelor şi
şi  ?Ce rezultă dacă
?Ce rezultă dacă  şi
şi  care sunt numere prime între ele?
care sunt numere prime între ele? 
Raţionamentul meu privind rezolvarea ecuaţiei propuse de mine:
^2=2z^2-2xy}) şi
şi ^2=2z^2+2xy}) de unde rezultă
de unde rezultă ^2+(x+y)^2=4z^2}) şi deci
şi deci
 unde
unde  sunt numere impare prime între ele şi în concluzie obţinem
sunt numere impare prime între ele şi în concluzie obţinem  .
.
Care sunt formulele de găsire a numerelor
Raţionamentul meu privind rezolvarea ecuaţiei propuse de mine:
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
E bun și raționamentul tău Dacu.
Mi se pare o idee mică ceva mai complicat.
Într-adevăr, trebuia menționat în mesajul meu anterior că prin modul acela de determinare a soluțiilor primitive, u și v trebuie să fie ambele impare, prime între ele.
Din dezvoltarea respectivă, rezultă evident, atât din modul în care ai dezvoltat tu, cât și din modul în care am dezvoltat eu, că pătratul lui z trebuie să fie obligatoriu suma a două pătrate perfecte.
Și prin metoda mea, cu u, v impare prime între ele, se găsesc toate soluțiile primitive.
Mi se pare o idee mică ceva mai complicat.
Într-adevăr, trebuia menționat în mesajul meu anterior că prin modul acela de determinare a soluțiilor primitive, u și v trebuie să fie ambele impare, prime între ele.
Din dezvoltarea respectivă, rezultă evident, atât din modul în care ai dezvoltat tu, cât și din modul în care am dezvoltat eu, că pătratul lui z trebuie să fie obligatoriu suma a două pătrate perfecte.
Și prin metoda mea, cu u, v impare prime între ele, se găsesc toate soluțiile primitive.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Dar se pare că am menționat, incomplet însă, ai dreptate.
Așadar, iei doar două impare prime între ele.
Dacă au aceeași paritate și alegem două pare, sau chiar și două impare cu divizor comun, evident, se vor găsi soluțiile care au un divizor comun.curiosul a scris:Rezolvarea evidentă este următoarea.Dacu a scris:Să se rezolve ecuaţiaunde
.
În primul rând, x și y nu pot avea paritate diferită, pentru căeste un număr par, iar dacă x și y au paritate diferită, atunci suma pătratelor lor va fi un număr impar, în timp ce
este un număr par.
Deci x și y au aceeași paritate.
Așadar, iei doar două impare prime între ele.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Acum, dacă înlocuim pătratul lui z cu un număr întreg, am putea spune că dacă dublul unui număr este sumă de două pătrate perfecte, atunci și numărul respectiv este sumă de două pătrate perfecte.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Repet:curiosul a scris:E bun și raționamentul tău Dacu.
Mi se pare o idee mică ceva mai complicat.
Într-adevăr, trebuia menționat în mesajul meu anterior că prin modul acela de determinare a soluțiilor primitive, u și v trebuie să fie ambele impare, prime între ele.
Din dezvoltarea respectivă, rezultă evident, atât din modul în care ai dezvoltat tu, cât și din modul în care am dezvoltat eu, că pătratul lui z trebuie să fie obligatoriu suma a două pătrate perfecte.
Și prin metoda mea, cu u, v impare prime între ele, se găsesc toate soluțiile primitive.
Fără supărare ,dar raţionamentul tău este în continuare incomplet şi tragi chiar şi concluzii greşite (după ce eu îţi arăt raţionamentul corect de rezolvare şi deci şi soluţiile corecte ale ecuaţiei propuse de mine) deoarece tu nu dai formulele de găsire ale numerelor
Ce valoare are
Fara supărare ,dar am propus această ecuaţie doar că să-ţi arăt că afirmaţia ta privind această ecuaţie de la subiectul tău "S-o numim conjectură......." este suspectă şi deci s-a dovedit a fi falsă.......
Nu mai încerca să dregi busuiocul cu alte şi alte afirmaţii atâta timp cât nu eşti sigur de ceea ce afirmi şi deci fii cinstit şi recunoaşte că ai greşit.......
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
S-o luăm altfel
De la ajungi la
ajungi la ^2+\left&space;(\frac{x-y}{2}&space;\right&space;)^2}) , unde z,
, unde z,  și
și  sunt triplete pitagoreice.
sunt triplete pitagoreice.
Poți așadar, să găsești x și y din
 și
și  , cu
, cu  și poți obține x, y, z exprimat în funcție de u și v.
și poți obține x, y, z exprimat în funcție de u și v.
Exemplele pe care le-ai dat vorbește despre faptul că nu ai fost atent la ce am afirmat
 este un număr întreg ???
este un număr întreg ???
De aia nici nu am mai insistat asupra lui.
Dar, pentru cealaltă, nu.
Să presupunem că .
.
Dacă dublul lui c este o sumă de două pătrate perfecte, atunci c este de asemenea, o sumă de două pătrate perfecte, pentru că se ajunge la


^2+(a-b)^2=4c})
^2+(\frac{a-b}{2})^2=c})
Nu este evident ?
Mai ține cont de faptul că dacă are soluții întregi, atunci a și b au aceeași paritate, ceea ce înseamnă că
are soluții întregi, atunci a și b au aceeași paritate, ceea ce înseamnă că  și
și  sunt numere întregi, deci c este la rândul lui o sumă de două pătrate perfecte.
sunt numere întregi, deci c este la rândul lui o sumă de două pătrate perfecte.
De aici, din ce ai dedus tu
 .
.
Dacă egalitatea de mai sus are soluții întregi, atunci z trebuie să poată fi exprimat de asemenea ca sumă de două pătrate perfecte.
Și vezi că ai câteva greșeli simple, pe care nu le-am mai menționat, gândindu-mă că sunt doar de redactare, deși am înțeles ce vrei să spui
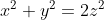 , atunci...vezi că semnele din dreapta egalităților sunt greșite.
, atunci...vezi că semnele din dreapta egalităților sunt greșite.
De la
Poți așadar, să găsești x și y din
Exemplele pe care le-ai dat vorbește despre faptul că nu ai fost atent la ce am afirmat
Dacă u și v sunt 13 și 5, atuncicuriosul a scris:
de unde rezultă că ecuația inițială trebuie să fie una de forma
cu,
,
Acestea sunt soluțiile.
Alegând u, v prime între ele, obținem toate soluțiile primitive ale ecuației.
Celelalte derivă din acestea.
Corect !Dacu a scris:Fara supărare ,dar am propus această ecuaţie doar că să-ţi arăt că afirmaţia ta privind această ecuaţie de la subiectul tău "S-o numim conjectură......." este suspectă şi deci s-a dovedit a fi falsă...
De aia nici nu am mai insistat asupra lui.
Recunosc că am greșit în ceea ce privește S-o numim conjectură...Dacu a scris:Nu mai încerca să dregi busuiocul cu alte şi alte afirmaţii atâta timp cât nu eşti sigur de ceea ce afirmi şi deci fii cinstit şi recunoaşte că ai greşit...
Dar, pentru cealaltă, nu.
Să presupunem că
Dacă dublul lui c este o sumă de două pătrate perfecte, atunci c este de asemenea, o sumă de două pătrate perfecte, pentru că se ajunge la
Nu este evident ?
Mai ține cont de faptul că dacă
De aici, din ce ai dedus tu
cu m, n având aceeași paritate, adică sunt ambele impare, din exprimarea lui z rezultă căDacu a scris: deciunde
sunt numere impare prime între ele şi în concluzie obţinem
.
Dacă egalitatea de mai sus are soluții întregi, atunci z trebuie să poată fi exprimat de asemenea ca sumă de două pătrate perfecte.
Și vezi că ai câteva greșeli simple, pe care nu le-am mai menționat, gândindu-mă că sunt doar de redactare, deși am înțeles ce vrei să spui
DacăDacu a scris:
Raţionamentul meu privind rezolvarea ecuaţiei propuse de mine:şi
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
curiosul,
Eşti incorijibil!!!!Chiar nu vezi ce greşeli ai postat???După ce mai întâi spui că şi că
şi că  sunt numere prime între ele şi apoi spui că
sunt numere prime între ele şi apoi spui că  sunt numere impare prime între ele fără a spune care sunt de fapt formulele de generare ale numerelor
sunt numere impare prime între ele fără a spune care sunt de fapt formulele de generare ale numerelor  mai şi afirmi sus şi tare că relaţiile date de mine şi anume
mai şi afirmi sus şi tare că relaţiile date de mine şi anume ^2=2z^2-2xy}) şi
şi ^2=2z^2+2xy}) sunt greşite...Asta denotă că ori habar nu ai ce spui ori vrei să acoperi greşelile tale continuând a-ţi susţine aceleaşi aberaţii şi jignindu-mă pe mine crezând că ceilalţi forumişti nu vor vedea ce aberaţii susţii tu.....Dacă tu nu recunoşti că ai greşit atunci asta denotă că tu eşti un om fără scrupule şi comportamentul tău este unul meschin.....
sunt greşite...Asta denotă că ori habar nu ai ce spui ori vrei să acoperi greşelile tale continuând a-ţi susţine aceleaşi aberaţii şi jignindu-mă pe mine crezând că ceilalţi forumişti nu vor vedea ce aberaţii susţii tu.....Dacă tu nu recunoşti că ai greşit atunci asta denotă că tu eşti un om fără scrupule şi comportamentul tău este unul meschin..... 






Eşti incorijibil!!!!Chiar nu vezi ce greşeli ai postat???După ce mai întâi spui că







Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Așa-i, ai dreptate !
Mă bucur că nu te-ai schimbat, ceea ce am și vrut să văd de altfel.
Mă bucur că nu te-ai schimbat, ceea ce am și vrut să văd de altfel.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Nu va certati ...a gresi este omenesc.Dacu a scris:curiosul,
Eşti incorijibil!!!!Chiar nu vezi ce greşeli ai postat???După ce mai întâi spui căşi că
sunt numere prime între ele şi apoi spui că
sunt numere impare prime între ele fără a spune care sunt de fapt formulele de generare ale numerelor
mai şi afirmi sus şi tare că relaţiile date de mine şi anume
şi
sunt greşite...Asta denotă că ori habar nu ai ce spui ori vrei să acoperi greşelile tale continuând a-ţi susţine aceleaşi aberaţii şi jignindu-mă pe mine crezând că ceilalţi forumişti nu vor vedea ce aberaţii susţii tu.....Dacă tu nu recunoşti că ai greşit atunci asta denotă că tu eşti un om fără scrupule şi comportamentul tău este unul meschin.....






Nu am urmarit calculele voastre dar asa la "o privire sumara" la nivelul clasei a 7-a Dacul are dreptate.Cele doua relatii sunt corecte
La prima citire in graba si eu le-am vazut gresite noroc ca nu am apucat sa postez.
Asa ca inainte de a posta ceva Curiosule te rog sa verifici de doua ori ca ulterior nu mai poti corecta si de dai de un specialist in matematica de clasa a 7-a cum este Dacul risti sa te faca cu ou si otet
Dacule Dacule ...iar ma dezamagesti !

Vizitator- Vizitator
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Mezei Geza,
Errare humanum est sed perseverare diabolicum. (Seneca)
Ai grijă să nu greşeşti nici tu de prea multe ori în aceiaşi privinţă....


Uite şi tu ce răspunsuri poate să dea curiosul "premiantul" şi dacă îl apucă iar criza o să ceară ca toate mesajele lui de la acest subiect să fie şterse ca să nu mai vadă nimeni aberaţiile pe care le-a postat........

 Noroc că nu mai este moderator.......
Noroc că nu mai este moderator....... 
Vezi mai bine dacă eu am rezolvat bine ecuaţia propusă de mine.....


Errare humanum est sed perseverare diabolicum. (Seneca)
Ai grijă să nu greşeşti nici tu de prea multe ori în aceiaşi privinţă....
Uite şi tu ce răspunsuri poate să dea curiosul "premiantul" şi dacă îl apucă iar criza o să ceară ca toate mesajele lui de la acest subiect să fie şterse ca să nu mai vadă nimeni aberaţiile pe care le-a postat........


 Noroc că nu mai este moderator.......
Noroc că nu mai este moderator....... Vezi mai bine dacă eu am rezolvat bine ecuaţia propusă de mine.....
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Greseala pe care o face frecvent Curiosul este ca posteaza direct fara o analiza temeinica.In matematica sau mai exact in toate stiintele exacte intai analizezi de "Ţ" ori si expui o singura data.
In rest toata stima pentru el.Este printre putinii dintre noi care lucreaza la greu, nu numai comenteaza sau scrie literatura SF.Sa am eu energia si motivatia lui deja teoria Globala era de mult gata.
Am sa ma uit peste demonstratii si dau o parere
In rest toata stima pentru el.Este printre putinii dintre noi care lucreaza la greu, nu numai comenteaza sau scrie literatura SF.Sa am eu energia si motivatia lui deja teoria Globala era de mult gata.
Am sa ma uit peste demonstratii si dau o parere
Vizitator- Vizitator
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Exact Geza !
Asta-i problema.
Îmi tună ceva prin cap, scriu, într-adevăr, de multe ori fără o analiză atentă în prealabil, iar după aia îmi dau seama și singur ce-i greșit și ce nu.
Cred că aici trebuie să mai lucrez.
Asta-i problema.
Îmi tună ceva prin cap, scriu, într-adevăr, de multe ori fără o analiză atentă în prealabil, iar după aia îmi dau seama și singur ce-i greșit și ce nu.
Cred că aici trebuie să mai lucrez.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
In ecuatia pitagoreica se spune daca nu gresesc ca m,n trebue sa fie naturale nu intregi, asa ca mai tae din coadaDacu a scris:Fără supărare ,dar raţionamentul tău este incomplet........
Care sunt formulele de găsire a numerelorşi
?Ce rezultă dacă
şi
care sunt numere prime între ele?

Raţionamentul meu privind rezolvarea ecuaţiei propuse de mine:şi
de unde rezultă
şi deci
unde
sunt numere impare prime între ele şi în concluzie obţinem
.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
meteor,
Daca Pitagora nu cunoştea numerele întregi asta nu înseamnă că o ecuaţie de tipul celei propuse de mine nu se poate rezolva în numere întregi........
Daca Pitagora nu cunoştea numerele întregi asta nu înseamnă că o ecuaţie de tipul celei propuse de mine nu se poate rezolva în numere întregi........

Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: O ecuaţie uşor de rezolvat.....
Re: O ecuaţie uşor de rezolvat.....
Sigur Dacule, mai mult, chiar dacă sunt întregi, prin ridicarea acestora la pătrat, ecuația devine una în N.Dacu a scris:meteor,
Daca Pitagora nu cunoştea numerele întregi asta nu înseamnă că o ecuaţie de tipul celei propuse de mine nu se poate rezolva în numere întregi...
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 