Interpretarea geometrică a ecuației x^n+y^n=z^n

Aseară, tot gândindu-mă la ecuația marii teoreme a lui Fermat, am ajuns la o problemă referitoare la algebrizarea geometriei, dacă m-am exprimat corect.
Și asta pentru că, algebric, putem lucra cu infinit, cu limite la infinit și așa mai departe, în timp ce din punct de vedere geometric, infinitul ridică anumite probleme.
Pentru că dacă putem considera că o dreaptă are x unități, atunci acea unitate este definită cumva deși ea trebuie să aibă un număr infinit de puncte. Deci unitatea însăși nu este definită, ci conține o infinitate de puncte.
Pentru că dacă am considera o unitate ca fiind cea mai mică, indivizibilă, atunci am putea considera că un segment este bine definit și are x unități, ceea ce ar însemna că folosind principii algebrice am avea împărțiri inexacte, iar este imposibil pentru că unitatea aceea este indivizibilă, este cea mai mică, și nu putem vorbi de 1,5 unități indivizibile. Nu știu ce se înțelege din ceea ce vreau să spun, dar în esență, nu putem vorbi de un segment finit ce are x unități,  deci implicit nu putem vorbi de operații algebrice bine definite pentru a descrie forme  geometrice sau relații între ele.
Și multe altele, dar nu continui aici, ci probabil o să deschid un nou subiect altădată, când voi avea ceva concret de spus, pentru că din aceste considerente cred că există o problemă în extinderea algebrei spre geometrie, sau invers, și demonstrația unor probleme algebrice folosind principii geometrice.
Nu mi se pare corect, și cred că geometria nu poate fi algebrizată și nici invers.

În fine, să trec la ce mă interesează și la ce vreau să întreb în acest subiect.
Tot dezvoltând aseară subiectul și gândindu-mă la acel faimos pi, mi-am amintit ce am analizat odată vis-a-vis de ecuația lui Fermat.
Așa cum scrie și pe wikipedia la un moment dat, ecuația cercului poate fi .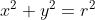

Țin minte că și eu analizasem odată ceva asemănător.
Să presupunem că avem un cerc de diametru z. Segmentele obținute de un punct de pe linia cercului și capetele diametrului formează un unghi de 90 de grade și putem interpreta ecuația cercului ca fiind , cu x, y reale, și ca în animația de mai jos :



Am mai făcut eu în acel moment nu-ș' ce calcule, la fel...de personale, și printr-o metodă asemănătoare, adică toate soluțiile x, y, n  reale, pentru care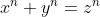 , cu z fix, ar trebui să descrie o elipsă, ca în animațiile de mai jos, prima pentru z fixat reprezentând axa mică și n real mai mare ca 2, iar a doua pentru z fixat reprezentând axa mare și n mai mic ca 2, dar mai mare ca 1.






Ceea ce vreau să întreb pe cei care cunosc și au studiat mai bine elipsele este dacă prin modul în care am interpretat eu situația, ecuația elipsei  ar putea fi și descrisă de ecuația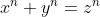 , unde z este fixat și reprezintă axa mică a elipsei (pentru n > 2), sau axa mare după caz (pentru 1 < n < 2), iar x, y sunt toate soluțiile reale pentru care

x și y sunt segmentele obținute de orice punct de pe elipsă și capetele axei (mari sau mici).

Uite ce zice Wolfram pentru ecuaţia unde n=2
http://www.wolframalpha.com/input/?i=plot+x%5En%2By%5En%3Dz%5En+where+n%3D2

Da Răzvane, dar eu mă gândeam doar la modul în care am interpretat eu situația și ecuația la nivel geometric.

Iar acum îmi dau seama că are cumva legătură și cu demonstrația lui Andrew Wiles a acestei teoreme prin acele curbe eliptice, pe care, evident, n-o cunosc și nici n-aș înțelege-o.

Și asta pentru că

Ceea ce înseamnă că trebuie să existe un cerc de diametru și o elipsă (de ordin n, să-i spunem) cu axa mică z, dacă n este mai mare ca 2.
Deci ar trebui să fie și un cerc și o elipsă simultan.

Iar suprafața acelei elipse ar trebui să fie radical de ordin n/2 din suprafața acelui cerc, calculat așa la repezeală.

Razvan a scris:Uite ce zice Wolfram pentru ecuaţia unde n=2
http://www.wolframalpha.com/input/?i=plot+x%5En%2By%5En%3Dz%5En+where+n%3D2

Dacă şi sunt numere naturale atunci ecuaţia impune ca şi aceast fapt se demonstrează foarte uşor.
În sistemul ortogonal de axe XOY dacă notăm şi ,atunci putem spune că pentru orice valori naturale date ale lui :
1) reprezintă o dreaptă.
2) reprezintă un cerc.
3) reprezintă o curbă deschisă
4) reprezintă o curbă închisă.
Ce poate reprezenta pentru şi pentru unde ?
---------------------------
Nu înţeleg de ce unii văd pe undeva vreo elipsă!!!!!Ce este o elipsă????Dacă valoarea lui tinde la infinit atunci ce reprezintă ?
Dacă valoarea lui tinde la infinit atunci ce reprezintă ?

Aseară,vântul bătea şi unu' elipse vedea...

Razvan a scris:Uite ce zice Wolfram pentru ecuaţia unde n=2
http://www.wolframalpha.com/input/?i=plot+x%5En%2By%5En%3Dz%5En+where+n%3D2

Rectific:
Dacă şi sunt numere naturale atunci ecuaţia impune ca şi aceast fapt se demonstrează foarte uşor.
În sistemul ortogonal de axe XOY dacă notăm şi ,atunci putem spune că pentru orice valori date ale lui :
1) reprezintă o dreaptă.
2) reprezintă un cerc.
3) reprezintă o curbă deschisă
4) reprezintă o curbă închisă.
Ce poate reprezenta pentru şi pentru unde ?
---------------------------
Nu înţeleg de ce unii văd pe undeva vreo elipsă!!!!!Ce este o elipsă????Dacă valoarea lui tinde la infinit atunci ce reprezintă ?
Dacă valoarea lui tinde la infinit atunci ce reprezintă ?

O fi Dacule și cum spui tu, dar hai să-ți explic cum și ce-am calculat eu de-am ajuns la concluzia asta.

L-am fixat pe z, adică i-am dat o valoare anume, considerând-o un segment, și am încercat să găsesc soluțiile x, y reale care construiesc triunghiul pentru care x^n+y^n=z^n, în condițiile în care x,y, z sunt laturile unui triunghi.
Am ales pentru început un n, după care un alt n, și un alt n, și așa mai departe.
Am considerat să spunem n=3 și inițial că x este egal cu y, deci triunghiul este isoscel, iar de la el plecăm doar într-o parte, deci construim doar un sfert de cerc sau de elipsă, așa cum le-am desenat eu cu vârful format de laturile x și y.
Am folosit un calculator, cunoscând valoarea lui z, am dat valori consecutive uneia dintre celelalte două, așa am aflat-o și pe cealaltă, după care am construit triunghiul format de aceste valori, x, y și z fixat.

Am observat că pentru n=2, vârfurile formate de x și y, descriu un sfert de cerc, iar pentru n mai mare ca 2 vârfurile formate de laturile x și y descriu un fel de curbă...asemănătoare unei elipse.


De aia am întrebat dacă ecuația elipsei s-ar putea reduce la ecuația lui Fermat, iar excentricitatea elipsei dată de valoarea lui n.

Că mă înșel, este posibil, eu îți spun doar ce-am analizat, de aia am întrebat.