Fractali și forme modulare

Scris de curiosul Mar 06 Ian 2015, 12:47

Am găsit de ceva timp o chestie interesantă vis-a-vis de ecuația teoremei lui Fermat pe care nu știu dacă o interpretez corect la nivel de formă modulară, dar este cumva legată de modul prin care s-a demonstrat Marea teoremă a lui Fermat.

Să vorbim mai întâi, oarecum introductiv, despre un mod...diferit de înțelegere și vizualizare a fractalilor, printr-o exprimare...matematică, să-i spunem.

Să plecăm de la o egalitate simplă de genul x+y=z.
Evident, matematic avem x=z-y și y=z-x.
Înlocuind în egalitatea inițială valorile lui x și y de mai sus am avea egalitatea (z-y)+(z-x)=z.
Înlocuind din nou oricare dintre valorile x,y,z cu valorile corespunzătoare lor, și anume x=z-y , y=z-x, x+y=z, ajungem la o formă de genul:
(x+y)-(z-x)+(x+y)-(z-y)=(x+y)
și mai mult
(z-y)+(z-x)-((x+y)-(z-y))+(z-y)+(z-x)-((x+y)-(z-x))=(z-y)+(z-x)
etc.

Observăm că înlocuind într-un mod asemănător oricare valoare x, y sau z din egalitate ajungem întotdeauna la o formă asemănătoare, care se reduce într-un final doar la egalitatea x+y=z, egalitate care după cum se vede mai sus are o definiție simplă și recursivă, se obțin aceleași detalii cu cele ale egalității inițiale, fiind o formă repetitivă a aceluiași pas, iar și iar.
Cu alte cuvinte, o structură matematică de tip fractal, o formă modulară.

Nu întâmplător am ales pentru început acestă modalitatea de vizualizare a fractalilor.
Dacă încercăm însă să să folosim puteri, prin dezvoltarea lor folosind binomul lui Newton apare o chestie interesantă.
Pentru n mai mare ca 2, cu cazul n=3 la limită, nu putem ajunge la o formă modulară.
Și anume.

Să explic cum văd lucrurile pentru cazul n=2 și cazul la limită n=3.
Să încercăm să ajungem la o egalitate care face posibilă cumva, modificarea puterii fără a schimba valoarea egalității, printr-un principiu asemănător celui prezentat anterior.
Pentru cazul n=2 o putem deduce:

$( x+y-z)^2=2(z-x)(z-y)+{\color{Red} x^2+y^2-z^2}$

Vorbeam mai sus de modificarea puterii fără a schimba valoarea egalității.

Să considerăm că în egalitatea anterioară x+y=z. Evident membrul stâng (paranteza la pătrat) se anulează și vom avea :

$0=2(z-x)(z-y)+{\color{Red} x^2+y^2-z^2}$

Dacă x+y=z, atunci x=z-y și y=z-x, valori pe care le putem înlocui și obținem :

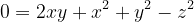
$0=2xy+ x^2+y^2-z^2$

$z^2=2xy+ x^2+y^2=(x+y)^2$

și evident obținem că x+y=z.
Să considerăm acum că $x^2+y^2=z^2$ iar în egalitatea

$( x+y-z)^2=2(z-x)(z-y)+{\color{Red} x^2+y^2-z^2}$

termenii scriși cu roșu se vor anula iar egalitatea devine :

$(x+y-z)^2=2(z-x)(z-y)$

egalitate adevărată doar dacă $x^2+y^2=z^2$ .

Pentru cazul n=3 putem deduce egalitatea:

$(x+y-z)^3=3(x+y)(z-x)(z-y)+{\color{Red} x^3+y^3-z^3}$

În mod similar, considerând că x+y=z, membrul stâng se anulează și egalitatea devine :

$0=3xy(x+y)+{\color{Red} x^3+y^3-z^3}$

egalitate evidentă dacă x+y=z.
Dacă vom considera că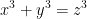 $x^3+y^3=z^3$ atunci ajungem la egalitatea

$(x+y-z)^3=3(x+y)(z-x)(z-y)$

desigur, egalitate adevărată dacă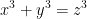 $x^3+y^3=z^3$ .
Precizam la un moment dat că acest caz n=3 este un caz la limită pentru că valoarea x+y rămâne invariantă la schimbarea puterii, deși se poate ajunge la aceste egalități.

Dacă încercăm să găsim egalități asemănătoare pentru n>3, exprimate în funcție de z-x, z-y care să permită aceste transformări din x în z-y și din y în z-x, pare imposibil.

Știe cineva dacă există analize asemănătoare pe undeva ?