Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Meteorr Ieri la 21:34
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Joi 21 Noi 2024, 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la CAdi în Sa mai auzim si de bine in Romania :
( 1 )
» Mesaj de la virgil în Fiinte deosebite.
( 1 )
» Mesaj de la CAdi în Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Dacu2 | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Abel Cavaşi |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| virgil | ||||
| Dacu2 | ||||
| Meteorr | ||||
| ilasus | ||||
| CAdi | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 39 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 39 Vizitatori :: 1 Motor de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Pagina 1 din 1
 Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
In teoria numerelor prime, a sti functiile care aproximeaza cit mai exact functia ) , ma refer la :
, ma refer la : \leq \pi (x)\leq M(x)) , in dependenta de continutul problemei si de cit de mult aproximeaza functia, inseamna a rezolva din o lovitura o multime de conjecturi nerezolvate..
, in dependenta de continutul problemei si de cit de mult aproximeaza functia, inseamna a rezolva din o lovitura o multime de conjecturi nerezolvate..
Sau, a determina cit mai precis constanta lui Legendre. Ca in figura urmatoare:

Stiinduse cit mai exact constanta lui Legendre, sau determininduse pe fiecare interval dorit, la fel inseamna a putea rezolva o multime de conjecturi..
La demonstrarea inegalitatilor este bine (necesar) ca sa se dea valorile minime posibile martii care arata ca este mai mare.
Insa, atentie!, deseori, din cauza anumitor factori (fie ca nu ne aproximam suficient de cutarea inegalitate), daca nu demonstram cu noile instrumente inegalitatea, nu inseamna ca inegalitatea e falsa.
Si, paradoxalul, daca demonstram ca e adevarata inegalitatea cu aproximarile aduse, atunci inegalitatea este adevarata.
Fooarte multe probleme [voi incepe a le prezenta] se rezolva foarte simplu daca se lucreaza cu functiile, si mai ales la unele proprietati caracteristice functiei cutare, la fel cu translatiile si rotatiile functiei.
Exsista unele probleme interesante, la care se rezolva prin o simpla determinare daca formeaza asimptote, serii convergente sau divergente...
Sau, a determina cit mai precis constanta lui Legendre. Ca in figura urmatoare:

Stiinduse cit mai exact constanta lui Legendre, sau determininduse pe fiecare interval dorit, la fel inseamna a putea rezolva o multime de conjecturi..
La demonstrarea inegalitatilor este bine (necesar) ca sa se dea valorile minime posibile martii care arata ca este mai mare.
Insa, atentie!, deseori, din cauza anumitor factori (fie ca nu ne aproximam suficient de cutarea inegalitate), daca nu demonstram cu noile instrumente inegalitatea, nu inseamna ca inegalitatea e falsa.
Si, paradoxalul, daca demonstram ca e adevarata inegalitatea cu aproximarile aduse, atunci inegalitatea este adevarata.
Fooarte multe probleme [voi incepe a le prezenta] se rezolva foarte simplu daca se lucreaza cu functiile, si mai ales la unele proprietati caracteristice functiei cutare, la fel cu translatiile si rotatiile functiei.
Exsista unele probleme interesante, la care se rezolva prin o simpla determinare daca formeaza asimptote, serii convergente sau divergente...
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Atentie mai mare la desenul atasat mai sus, si la semnificatia inegalitatilor.
In desen se arata ca graficele functiilor minime /maxime (numite asa de mine), daca este functia minim atunci ea niciodata nu va depasi (fie pe un anumit interval fie deloc) functia numerelor prime. In cazul cind este exasct egala (desigur doar si numai dar pe anumite puncte, pe intreg interval e imposibil, caci functia numerelor prime are o infinitate de puncte de influxiune, insa functia care aproximeaza este doar convexa si atit.)atunci este super.
La fel este e si cu functia maxim (despre posibilele aplicatiile [mari] ale ei, mai tirziu..), ea niciodata nu trebue sa "incalce" functia numerelor prime, poate sa se "atinga" de ea, INSA niciodata sa nu "paseasca" unele valor.
Ce spune inegalitatea -\leq \pi (x)\leq M(x)) ?!
?!
Ea spune ca functia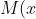) niciodata nu este mai mare ca
niciodata nu este mai mare ca ) . La fel spune ca functia
. La fel spune ca functia 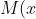) niciodata nu poate fi mai mica ca
niciodata nu poate fi mai mica ca ) , pe domeniu ei de definitie.
, pe domeniu ei de definitie.
Lucrati cu functiile si graficile lor, stuciatile, caci ele sunt o minune. Eu foarte greu (cred ca imposibil) sa rezolvi ceva mai complicat fara a aplica studiul functiilor si graficele(desigur ca graficile ajuta doar la perceptia mai buna) lor.
Ce inseamna asimptota?!
"Babeste" spus, asimptota este o functie care tinde, aproximeaza o anumita functie extrem de apropiat, INSA, niciodata nu descrie exsact.
Deaceea probabil si asa sau botezat : "Teorema numerelor prime descrie distribuția asimptotică a numerelor prime.".
De la wiki:
Titlul figurii fiind: "Graficul comparatiei dintre) [cu albastru] si
[cu albastru] si }) [cu verde]".
[cu verde]".
Acum, de ce nu ar fi gresit sa aplicam la unele probleme functia minum ca fiind}) (ok, fie pentru x-ul mai mare ca 360000 [pina acolo a verifica cu mina sau cu un program nu e nici o catastrofa])?!
(ok, fie pentru x-ul mai mare ca 360000 [pina acolo a verifica cu mina sau cu un program nu e nici o catastrofa])?!
Spre exemplu:
Pirre Dusart a gasit (demonstrat, si daca lumea spune ca el a demonstrat, inseamna ca asa si e, fara ai intelege demonstrtia si a gasi contraargumente, e gresit sa spunem ca e fals) urmatoarele functii:
\leq \pi (x)\leq M(x))
-1}\right )_{x\geq 5393}\leq \pi (x)\leq \left ( \frac{x}{ln(x)-1.1}\right )_{x\geq 60184})
sau, altele si mai bune:
}\left ( 1+\frac{1}{ln(x)}+\frac{1.8}{ln^{2}(x)}\right ) \right )_{x\geq 32299}\leq \pi (x)\leq \left ( \frac{x}{ln(x)}\left ( 1+\frac{1}{ln(x)}+\frac{2.51}{ln^{2}(x)}\right ) \right )_{x\geq 355991})
In orice caz chiar si http://en.wikipedia.org/wiki/Prime_number_theorem#Bounds_on_the_prime-counting_function spune:
-(1-\varepsilon )}< \pi (x)< \frac{x}{ln(x)-(1+\varepsilon )},\varepsilon >0)
Eu, am folosit:
}< \pi (x))
E grest?! Nu, deoarece:
}< \frac{x}{ln(x)-(1-\varepsilon )}< \pi (x)< \frac{x}{ln(x)-(1+\varepsilon )},\varepsilon >0)
}) este cel mai mic, deoarece valoarea de la numitor este cea mai mare comparativ cu celelalte doua (deoarece acolo este ln(x)- o valoare oarecare).
este cel mai mic, deoarece valoarea de la numitor este cea mai mare comparativ cu celelalte doua (deoarece acolo este ln(x)- o valoare oarecare).
Sau sa nu fie atita invirteala ne uitam inca odata la:
}\left ( 1+\frac{1}{ln(x)}+\frac{1.8}{ln^{2}(x)}\right ) \right )_{x\geq 32299}\leq \pi (x)\leq \left ( \frac{x}{ln(x)}\left ( 1+\frac{1}{ln(x)}+\frac{2.51}{ln^{2}(x)}\right ) \right )_{x\geq 355991})
Eu spun ca:
}< \left ( \frac{x}{ln(x)}\left ( 1+\frac{1}{ln(x)}+\frac{1.8}{ln^{2}(x)}\right ) \right )_{x\geq 32299}\leq \pi (x)\leq \left ( \frac{x}{ln(x)}\left ( 1+\frac{1}{ln(x)}+\frac{2.51}{ln^{2}(x)}\right ) \right )_{x\geq 355991})
Deoarece, in a doua inegalitate are}) inmultita cu o valoare care, cert este ca este mai mare ca 1.
inmultita cu o valoare care, cert este ca este mai mare ca 1.
La urmea urmei, se pot relua toate "calculele" in loc de anticvariat sa fie noile functii.
Cine vrea sa-si bata capul, si cauta ceva bibliografie (cred ca bunisioara), cred ca e bine sa vada:
- http://public.gettysburg.edu/~dglass/spring04/chebyshev.pdf [mult am mai rascolit pina am dat de asa ceva, dar ce folos, ca multe nu is clare ].
].
- http://en.wikipedia.org/wiki/Prime_number_theorem#Bounds_on_the_prime-counting_function
- sa caute despre mareata conjectura a lui Legendre privitor la exsistenta acelei constante, care sa demonstrat, sa ne dea si noua sa vedem acea demonstratie, dar daca a ainteles-o, e si mai bine, sa neo spuna. Daca o determina, e bine.
- http://primes.utm.edu/howmany.shtml#pnt ( aici se mai vad si niste tabele)
In desen se arata ca graficele functiilor minime /maxime (numite asa de mine), daca este functia minim atunci ea niciodata nu va depasi (fie pe un anumit interval fie deloc) functia numerelor prime. In cazul cind este exasct egala (desigur doar si numai dar pe anumite puncte, pe intreg interval e imposibil, caci functia numerelor prime are o infinitate de puncte de influxiune, insa functia care aproximeaza este doar convexa si atit.)atunci este super.
La fel este e si cu functia maxim (despre posibilele aplicatiile [mari] ale ei, mai tirziu..), ea niciodata nu trebue sa "incalce" functia numerelor prime, poate sa se "atinga" de ea, INSA niciodata sa nu "paseasca" unele valor.
Ce spune inegalitatea -
Ea spune ca functia
Lucrati cu functiile si graficile lor, stuciatile, caci ele sunt o minune. Eu foarte greu (cred ca imposibil) sa rezolvi ceva mai complicat fara a aplica studiul functiilor si graficele(desigur ca graficile ajuta doar la perceptia mai buna) lor.
Ce inseamna asimptota?!
"Babeste" spus, asimptota este o functie care tinde, aproximeaza o anumita functie extrem de apropiat, INSA, niciodata nu descrie exsact.
Deaceea probabil si asa sau botezat : "Teorema numerelor prime descrie distribuția asimptotică a numerelor prime.".
De la wiki:

Titlul figurii fiind: "Graficul comparatiei dintre
Acum, de ce nu ar fi gresit sa aplicam la unele probleme functia minum ca fiind
Spre exemplu:
Pirre Dusart a gasit (demonstrat, si daca lumea spune ca el a demonstrat, inseamna ca asa si e, fara ai intelege demonstrtia si a gasi contraargumente, e gresit sa spunem ca e fals) urmatoarele functii:
sau, altele si mai bune:
In orice caz chiar si http://en.wikipedia.org/wiki/Prime_number_theorem#Bounds_on_the_prime-counting_function spune:
Eu, am folosit:
E grest?! Nu, deoarece:
Sau sa nu fie atita invirteala ne uitam inca odata la:
Eu spun ca:
Deoarece, in a doua inegalitate are
La urmea urmei, se pot relua toate "calculele" in loc de anticvariat sa fie noile functii.
Cine vrea sa-si bata capul, si cauta ceva bibliografie (cred ca bunisioara), cred ca e bine sa vada:
- http://public.gettysburg.edu/~dglass/spring04/chebyshev.pdf [mult am mai rascolit pina am dat de asa ceva, dar ce folos, ca multe nu is clare
- http://en.wikipedia.org/wiki/Prime_number_theorem#Bounds_on_the_prime-counting_function
- sa caute despre mareata conjectura a lui Legendre privitor la exsistenta acelei constante, care sa demonstrat, sa ne dea si noua sa vedem acea demonstratie, dar daca a ainteles-o, e si mai bine, sa neo spuna. Daca o determina, e bine.
- http://primes.utm.edu/howmany.shtml#pnt ( aici se mai vad si niste tabele)
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
--==Aplicarea postulatului lui Bertrand sau teoremei lui Serpinski==--
Observ ca multi au o slabiciune cu aceste teoreme,
Dupa parerea mea, aplicarea lor in demonstrarea multor conjecturi (rezolvarea problemelor) strict in forma bruta NU poate fi suficient pentru ca sa poti rezolva problema.
E nevoe de alte instrumente mai performante si mai puternice.
Spre exemplu a incerca a rezolva conjectura lui Andrica (in forma bruta) cu teorema lui Serpinski[darimite sa incerci cu teorema lui Cebisev] e vai si amar, repet dupa parerea mea.
De ce?!
Exemplu concret aplicat la rezolvarea conjecturii lui Andrica:
Teorema lui Serpinski spune ca intre numarul n si dublul lui exista cel putin 2 numere prime, adica:

Deci numerele prime consecutive urmate dupa sunt cel mult la distanta de
sunt cel mult la distanta de  si
si  .
.
A incerca a rezolva conjectura lui Andrica [cu asa aparataj] e aceeasi cum a rezolva inegalitatea:

Dupa calcule ajungem ca avem o functie de gradul doi, si, crescatoare [ceea ce deja inseamna ca totul e indemnat..]:

Solutiile sunt in intervalul:![\left [ 3,7 \right ]](http://latex.codecogs.com/gif.latex?\left [ 3,7 \right ])
Haz .., am demonstrat [cu aceasta metoda] ca pe acest interval conjectura lui Andrica e adevarata.
Observ ca multi au o slabiciune cu aceste teoreme,
Dupa parerea mea, aplicarea lor in demonstrarea multor conjecturi (rezolvarea problemelor) strict in forma bruta NU poate fi suficient pentru ca sa poti rezolva problema.
E nevoe de alte instrumente mai performante si mai puternice.
Spre exemplu a incerca a rezolva conjectura lui Andrica (in forma bruta) cu teorema lui Serpinski[darimite sa incerci cu teorema lui Cebisev] e vai si amar, repet dupa parerea mea.
De ce?!
Exemplu concret aplicat la rezolvarea conjecturii lui Andrica:
Teorema lui Serpinski spune ca intre numarul n si dublul lui exista cel putin 2 numere prime, adica:
Deci numerele prime consecutive urmate dupa
A incerca a rezolva conjectura lui Andrica [cu asa aparataj] e aceeasi cum a rezolva inegalitatea:
Dupa calcule ajungem ca avem o functie de gradul doi, si, crescatoare [ceea ce deja inseamna ca totul e indemnat..]:
Solutiile sunt in intervalul:
Haz .., am demonstrat [cu aceasta metoda] ca pe acest interval conjectura lui Andrica e adevarata.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Pentru a scapa de durerea de cap https://cercetare.forumgratuit.ro/t933-greseli-ce-nu-este-de-recomandat-sa-se-faca#26850 , care cert ca e adevarat, insa asa e in mate trebue demonstratie la orice miscare.
Se pare ca de nu subliniam necesitatea de a demonstra aceasta, multi erau sa inghita galusca.
Foarte posibil sa aiba o rezolvare mai simpla.
La moment eu cred ca rezolvarea consta in aceea in a demonstra ca inegalitatea nu admite contraargumente, sau chiar de le admite sa nu incalce cutarele conjecturi:
+1&space;\right&space;)^{-1})
Unde prin puterea la minus 1 s-a notat inversa acelei functii.
Se pare ca de nu subliniam necesitatea de a demonstra aceasta, multi erau sa inghita galusca.
Foarte posibil sa aiba o rezolvare mai simpla.
La moment eu cred ca rezolvarea consta in aceea in a demonstra ca inegalitatea nu admite contraargumente, sau chiar de le admite sa nu incalce cutarele conjecturi:
Unde prin puterea la minus 1 s-a notat inversa acelei functii.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Se poate alta varianta de solutionare a cutarii probleme, insa, are ceva neajunsuri mici: trebuie sa avem functiile minim si maxim sa aproximeze foare foarte bine functia numerelor prime, in caz contrar pasul pe care il gasim ca fiind distanta maxima posibila intre 2 numere consecutive, sa nu ne ajute la rezolvarea problemelor/ conjecturilor.
Dar si aici se poate merge mai departe. Adica functiile minim si maxim sa nu ,spre exemplu, fie cele gasite de P.Dusart, ci sa lucram, spre exemplu (si la fel spre comoditate) cu functia (constanta) lui Legendre.
Aici ideea consta in aceea, ca dupa citeva milioane, functie lui Legendre sare (din cite tin minte) peste functia numerelor prime.
Deci functia maxim am putea-o defini ca functia lui Legendre translata spre stinga-sus cu citeva unitati (as spune vreo 4) , insa functia minim va fi translatia (la ochi as spune ca cu vreo 4 unitati) spre dreapta- jos, si rotatia (sau modificarea infim de mica a constante) cu un unghi foarte mic, (aproximativ arctg(1/1000000).
Trebue si aici calcule si cercetari, ceva insa se poate face.
Cu rotatia cred ca vor fi batai de cap.
Folosind functiile lui P.Dusart (sau alte functii, repet de dorit cit mai bine sa aproximeze functia numerelor prime), numarul prim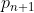 consecutiv lui
consecutiv lui  va fi gasit ca fiind solutia (desigur aici trebue selectata solutia potrivita..) ecuatiei:
va fi gasit ca fiind solutia (desigur aici trebue selectata solutia potrivita..) ecuatiei:
=M(p_{n})) (1)
(1)
Pentru cine nu intelege ce mai e aceasta:
 - este variabila , care trebue gasita
- este variabila , care trebue gasita
 - este un numar prim, deci o constanta
- este un numar prim, deci o constanta
) si
si ) sunt functii.
sunt functii.
Exemplu: Cine gaseste solutia urmatoarei ecuatii, gaseste aproximat pe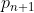 :
:
}\left&space;(&space;1+\frac{1}{\ln(n)}&space;\right&space;)=\frac{p_{n}}{\ln(p_n)}\left&space;(&space;1+\frac{1}{\ln(p_n)}+\frac{2.51}{\ln(p_n)}&space;\right&space;)) ,
, 
(Am incercat ceva cu WolframAlfa, insa nimic bun, si era de asteptat, deoarece functia) e definita de la un numar mare (5115937), in al doilea rind posibil da numai o singura solutie, si ea fiind straina celei pe care noi o cautam.
e definita de la un numar mare (5115937), in al doilea rind posibil da numai o singura solutie, si ea fiind straina celei pe care noi o cautam.
Fie caci cindva cineva va rezolva ecuatia (1), si va gasi solutia ei. Fie o vom nota cu .
.
Acum trebue de retinut ca:![p_{n+1}\in [p_n+2; s]](http://latex.codecogs.com/gif.latex?p_{n+1}\in&space;[p_n+2;&space;s])
Aplicatii: Spre exemplu a rezolva (atentie! fara nici o garantie! Daca se adevereste raspunsul inseamna ca conjectura e adevarata, daca nu nimic nu putem spune despre conjectura cutare, ci putem reprosa caci cu asa metode prea departe l-am aproximat pe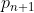 fata de
fata de  ) conjectura lui Andrica, nu ne ramine nimic altceva decit sa rezolvam inecuatia:
) conjectura lui Andrica, nu ne ramine nimic altceva decit sa rezolvam inecuatia:
 ,
,
[cam in asa fel se pot rezolva si alte probleme..]
Dar si aici se poate merge mai departe. Adica functiile minim si maxim sa nu ,spre exemplu, fie cele gasite de P.Dusart, ci sa lucram, spre exemplu (si la fel spre comoditate) cu functia (constanta) lui Legendre.
Aici ideea consta in aceea, ca dupa citeva milioane, functie lui Legendre sare (din cite tin minte) peste functia numerelor prime.
Deci functia maxim am putea-o defini ca functia lui Legendre translata spre stinga-sus cu citeva unitati (as spune vreo 4) , insa functia minim va fi translatia (la ochi as spune ca cu vreo 4 unitati) spre dreapta- jos, si rotatia (sau modificarea infim de mica a constante) cu un unghi foarte mic, (aproximativ arctg(1/1000000).
Trebue si aici calcule si cercetari, ceva insa se poate face.
Cu rotatia cred ca vor fi batai de cap.
Folosind functiile lui P.Dusart (sau alte functii, repet de dorit cit mai bine sa aproximeze functia numerelor prime), numarul prim
Pentru cine nu intelege ce mai e aceasta:
Exemplu: Cine gaseste solutia urmatoarei ecuatii, gaseste aproximat pe
(Am incercat ceva cu WolframAlfa, insa nimic bun, si era de asteptat, deoarece functia
Fie caci cindva cineva va rezolva ecuatia (1), si va gasi solutia ei. Fie o vom nota cu
Acum trebue de retinut ca:
Aplicatii: Spre exemplu a rezolva (atentie! fara nici o garantie! Daca se adevereste raspunsul inseamna ca conjectura e adevarata, daca nu nimic nu putem spune despre conjectura cutare, ci putem reprosa caci cu asa metode prea departe l-am aproximat pe
[cam in asa fel se pot rezolva si alte probleme..]
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Pina ce e ok.
http://www.wolframalpha.com/input/?i=%5Bx%2Flnx%5D%5B1%2B1%2Fln%28x%29%5D%3D%5B5115937%2Fln%285115937%29%5D%5B1%2B1%2Fln%285115937%29%2B2.51%2Fln%285115937%29%5D
Data trecuta nu am fost atent cind am introdus formula la WolframAlfa, acum am introdus corect.
Pentru (adica cea mai mica valoare de pe domeniul de definitie a functiilor),
(adica cea mai mica valoare de pe domeniul de definitie a functiilor),  este
este  .
.
Wolfram spune caci solutia noastra cautata este aproximativ , ceea ce deja inseamna ca lucrurile stau bine (aproximatia lui
, ceea ce deja inseamna ca lucrurile stau bine (aproximatia lui 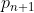 e destul de buna [in comparatie cu teorema lui Serpinschi sau postulatul lui Bertrand ] ) in realitate
e destul de buna [in comparatie cu teorema lui Serpinschi sau postulatul lui Bertrand ] ) in realitate  este
este 
INSA, nu e buna aproximatia lui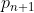 (e prea indepartata) la rezolvarea conjecturii lui Andrica http://www.wolframalpha.com/input/?i=sqrt%286000000%29-sqrt%285115937%29
(e prea indepartata) la rezolvarea conjecturii lui Andrica http://www.wolframalpha.com/input/?i=sqrt%286000000%29-sqrt%285115937%29
Daca luam functia m(n) ce aproximeaza putin mai bine functia numerelor prime:
http://www.wolframalpha.com/input/?i=%5Bx%2Flnx%5D%5B1%2B1%2Fln%28x%29%2B1.8%2Fln%28x%29%5D%3D%5B5115937%2Fln%285115937%29%5D%5B1%2B1%2Fln%285115937%29%2B2.51%2Fln%285115937%29%5D , in asa caz nu vad care e valoarea aproximativa a solutiei, insa precis ca nu e 6 milioane ci ceva in jur de 5.5 milioane, http://www.wolframalpha.com/input/?i=sqrt%285500000%29-sqrt%285115937%29 nici in asa caz nu dam de capat cu conjectura lui Andrica.
Pina la urma ramine de gasit solutia ecuatiei (1) si de gasit functii ce aproximeaza cit mai bine functia numerelor prime.
Mi se pare caci gasirea solutiilor se poate pe cale numerica, gasirea functiilor am spus cum se poate face.
Ramine de lucrat, pentru cine vrea
Daca se demonstreaza caci valorile solutiilor in inecuatia lui Andrica, aplicind aparatajul nostru, sunt convergente, si odata si odata scad sub 1, atunci se poate spune ca dupa un numar suficient de mare conjectura lui Andrica e adevarata (conform aparatajului nostru).
http://www.wolframalpha.com/input/?i=%5Bx%2Flnx%5D%5B1%2B1%2Fln%28x%29%5D%3D%5B5115937%2Fln%285115937%29%5D%5B1%2B1%2Fln%285115937%29%2B2.51%2Fln%285115937%29%5D
Data trecuta nu am fost atent cind am introdus formula la WolframAlfa, acum am introdus corect.
Pentru
Wolfram spune caci solutia noastra cautata este aproximativ
INSA, nu e buna aproximatia lui
Daca luam functia m(n) ce aproximeaza putin mai bine functia numerelor prime:
http://www.wolframalpha.com/input/?i=%5Bx%2Flnx%5D%5B1%2B1%2Fln%28x%29%2B1.8%2Fln%28x%29%5D%3D%5B5115937%2Fln%285115937%29%5D%5B1%2B1%2Fln%285115937%29%2B2.51%2Fln%285115937%29%5D , in asa caz nu vad care e valoarea aproximativa a solutiei, insa precis ca nu e 6 milioane ci ceva in jur de 5.5 milioane, http://www.wolframalpha.com/input/?i=sqrt%285500000%29-sqrt%285115937%29 nici in asa caz nu dam de capat cu conjectura lui Andrica.
Pina la urma ramine de gasit solutia ecuatiei (1) si de gasit functii ce aproximeaza cit mai bine functia numerelor prime.
Mi se pare caci gasirea solutiilor se poate pe cale numerica, gasirea functiilor am spus cum se poate face.
Ramine de lucrat, pentru cine vrea
Daca se demonstreaza caci valorile solutiilor in inecuatia lui Andrica, aplicind aparatajul nostru, sunt convergente, si odata si odata scad sub 1, atunci se poate spune ca dupa un numar suficient de mare conjectura lui Andrica e adevarata (conform aparatajului nostru).
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Daca se demonstreaza caci cam injur de dupa 1.000.000 functia lui Legendre =\frac{n}{\ln(n)-1.08366}) devine strict mai mare sau egala ca
devine strict mai mare sau egala ca ) , adica
, adica
\leq\left&space;(&space;\frac{n}{\ln(n)-1.08366}&space;\right&space;)&space;_{_{n>1.&space;000.000}})
atunci am avea de aface cu aproximatii mai bune.
Aproximatia lui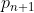 va fi solutia ecuatiei:
va fi solutia ecuatiei:
=L(p_{n}),n>1.000.000)
Deoarece ambele functii sunt strict convexe crescatoare si nu se intersecteaza pe domeniul in care lucram, la fel nu sunt translatii a unei din ele, cred ca ar fi corect sa spunem: e deajuns sa gasim 2 valori particulare pentru a spune cum sunt valorile solutiilor (convergente sau divergente).
Proba 1.

}\left&space;(&space;1+\frac{1}{ln(n)}+\frac{2.51&space;}{\ln^{2}(n)}&space;\right&space;)=\frac{p_{1.000.000}&space;}{\ln(p_{1.000.000})-1,08366})
Solutia 1. (s1) a aceste ecuatii, Wolfram nu spune pina ce nimic clar http://www.wolframalpha.com/input/?i=%28x%2Fln%28x%29%281%2B1%2Fln%28x%29%2B1.8%2F%28ln%5E2%28x%29%29%29%3D15485863%2F%28ln%2815485863%29-1.08366%29
Daca spunea ceva, atunci trebuia asa sa facem:

Apoi faceam proba doi:

Apoi ne raminea sa comparam cum este p1 fata de p2 pentru a putea spune daca solutiile sunt convergente.
Daca converg si cad sub 1 ... am spus .. inseamna ca dupa un numar mare conjectura e adevarata.
.. inseamna ca dupa un numar mare conjectura e adevarata.
* Cred ca e mai ok sa ma opresc, caci nestiintelegind cum s-au obtinut acele rezulte (de Cebisev, P.Dusart, Legendre, etc.) indata m-as face un electrician, sau un fizician cuantic, in orice caz cineva din teoria fanteziilor.
atunci am avea de aface cu aproximatii mai bune.
Aproximatia lui
Deoarece ambele functii sunt strict convexe crescatoare si nu se intersecteaza pe domeniul in care lucram, la fel nu sunt translatii a unei din ele, cred ca ar fi corect sa spunem: e deajuns sa gasim 2 valori particulare pentru a spune cum sunt valorile solutiilor (convergente sau divergente).
Proba 1.
Solutia 1. (s1) a aceste ecuatii, Wolfram nu spune pina ce nimic clar http://www.wolframalpha.com/input/?i=%28x%2Fln%28x%29%281%2B1%2Fln%28x%29%2B1.8%2F%28ln%5E2%28x%29%29%29%3D15485863%2F%28ln%2815485863%29-1.08366%29
Daca spunea ceva, atunci trebuia asa sa facem:
Apoi faceam proba doi:
Apoi ne raminea sa comparam cum este p1 fata de p2 pentru a putea spune daca solutiile sunt convergente.
Daca converg si cad sub 1 ... am spus
 .. inseamna ca dupa un numar mare conjectura e adevarata.
.. inseamna ca dupa un numar mare conjectura e adevarata.* Cred ca e mai ok sa ma opresc, caci nestiintelegind cum s-au obtinut acele rezulte (de Cebisev, P.Dusart, Legendre, etc.) indata m-as face un electrician, sau un fizician cuantic, in orice caz cineva din teoria fanteziilor.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
---------======= Rezumat ======--------
Pentru a putea rezulva multe probleme din teoria numerelor prime, o cale foarte importanta ar fi daca am aplica functiile minim si maxim.
Acolo principiul de baza consta in aceea ca: " Pentru a determina numarul minim de numere prime in intervalul [a,b], acesta ar fi egal cu m(b)-m(a)."
Adica in o oarecare masura ne-am concentrat pe aceea in a gasi distanta maxima dintre pn si pn+1.
INSA, s-a observat caci exista riscuri astfel incit in anumite cazuri distanta pe care noi am fi condiderat-o maxima, in realitate sa fie sub cea reala.
Fara a demonstra ca riscurile sunt false, demonstratiile cele din urma ramin incomplete.
Atentie la imaginea de mai jos , care explica absolut totul:
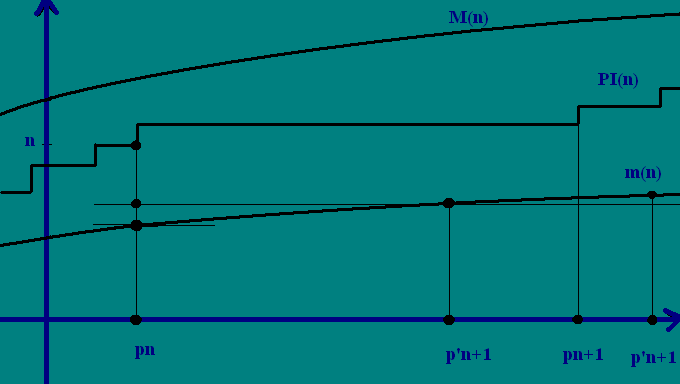
In desen se observa , caci axa X'OY' a fost mutata undeva mai sus si mai departe de XOY.
Se vede bine functia PI(n), m(n), M(n).
Se vede cum la un anumit pn, functia PI(pn) are valoare n, si m(pn) are o anumita valoare [desigur ea e strict mai mica sau egala cu n, deaceea doar si e functia minim].
Apoi s-a lasat anume ca urmatorul pn+1 sa fie amplasat la o distanta foarte giganta fata de pn.
Si aici poate sta visinica (contraargumentul) din virful tortului, caci aproximatia p'n+1 a lui pn+1 sa fie in anumite conditii (cind distanta e foarte giganta), p'n+1 sa fie mai mic ca pn+1.
Deci+1&space;\right&space;)^{-1}) (atentie! mai corect posibil ca este: Exprimarea lui
(atentie! mai corect posibil ca este: Exprimarea lui  in functie de
in functie de  din ecuatia:
din ecuatia: +1) , desigur ambelele vriabile sunt mia mari ca 0 )
, desigur ambelele vriabile sunt mia mari ca 0 )
Daca pe domeniul in care lucram, atunci lucrurile stau bine.
pe domeniul in care lucram, atunci lucrurile stau bine.
Problemele care stau la rezolvarea conjecturii lui Operman:

Desenul spune multe.
A doua metoda de al aproxima pe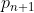 este ca el este solutia ecuatiei:
este ca el este solutia ecuatiei:
=M(x))
La fel ca la cazul precedent, desenul spune totul (acest desan ba e prea domol asa incit intre x si solutia: m(n)=M(x) sunt 2 numere prime. Se poate face un desen mai dur in care se arata bine ca cel putin un numar prim trebue sa fie intre x si solutia ecuatiei: m(n)=M(x)).

Dar, din cauza ca functiile noastre slab aproximeaza PI(n), noi prea departe il aproximam pe pn+1, deaceea nu putem iesi la capat macasr cu conjectura lui Andrica (acolo diferenta radicalilor abia coaboara pina la vreo 25).
Pentru a putea rezulva multe probleme din teoria numerelor prime, o cale foarte importanta ar fi daca am aplica functiile minim si maxim.
Acolo principiul de baza consta in aceea ca: " Pentru a determina numarul minim de numere prime in intervalul [a,b], acesta ar fi egal cu m(b)-m(a)."
Adica in o oarecare masura ne-am concentrat pe aceea in a gasi distanta maxima dintre pn si pn+1.
INSA, s-a observat caci exista riscuri astfel incit in anumite cazuri distanta pe care noi am fi condiderat-o maxima, in realitate sa fie sub cea reala.
Fara a demonstra ca riscurile sunt false, demonstratiile cele din urma ramin incomplete.
Atentie la imaginea de mai jos , care explica absolut totul:

In desen se observa , caci axa X'OY' a fost mutata undeva mai sus si mai departe de XOY.
Se vede bine functia PI(n), m(n), M(n).
Se vede cum la un anumit pn, functia PI(pn) are valoare n, si m(pn) are o anumita valoare [desigur ea e strict mai mica sau egala cu n, deaceea doar si e functia minim].
Apoi s-a lasat anume ca urmatorul pn+1 sa fie amplasat la o distanta foarte giganta fata de pn.
Si aici poate sta visinica (contraargumentul) din virful tortului, caci aproximatia p'n+1 a lui pn+1 sa fie in anumite conditii (cind distanta e foarte giganta), p'n+1 sa fie mai mic ca pn+1.
Deci
Daca
Problemele care stau la rezolvarea conjecturii lui Operman:

Desenul spune multe.
A doua metoda de al aproxima pe
La fel ca la cazul precedent, desenul spune totul (acest desan ba e prea domol asa incit intre x si solutia: m(n)=M(x) sunt 2 numere prime. Se poate face un desen mai dur in care se arata bine ca cel putin un numar prim trebue sa fie intre x si solutia ecuatiei: m(n)=M(x)).

Dar, din cauza ca functiile noastre slab aproximeaza PI(n), noi prea departe il aproximam pe pn+1, deaceea nu putem iesi la capat macasr cu conjectura lui Andrica (acolo diferenta radicalilor abia coaboara pina la vreo 25).
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Re: Ce e bine de stiut pentru rezolvarea multor conjecturi (probleme)?!
Uitasem a chita oara de mesajul acesta care impedica totul, adica spune caci cu actualele functii m(x) si M(x) prin metodele(algoritmul) propuse de mine (eu is absolut convins caci e corect) nu este si suficient macar a rezolva conjectura lui Andrica.
O propunere in a inbunatati m(x) si M(x) este o asa propunere:
A roti aceste grafice) si
si ) contra acelor de ceasornic cu unghiul
contra acelor de ceasornic cu unghiul  si in directia acelor de ciasornic cu unghiul
si in directia acelor de ciasornic cu unghiul  din anumite puncte cu anumite coordonate M(x1,y1) si P(x2,y2), ar trebui sa obtinem noi functii m(x) ca fiind
din anumite puncte cu anumite coordonate M(x1,y1) si P(x2,y2), ar trebui sa obtinem noi functii m(x) ca fiind ) si M(x) fiind
si M(x) fiind ) .
.

Unica problema care este pina aici e aceea caci trebue sa gasim acele unghiuri si important sa demonstram caci NU se incalca functia) pe intervalele semideschise definite
pe intervalele semideschise definite ) si
si )
O propunere in a inbunatati m(x) si M(x) este o asa propunere:
A roti aceste grafice

Unica problema care este pina aici e aceea caci trebue sa gasim acele unghiuri si important sa demonstram caci NU se incalca functia
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 