Clasificarea traiectoriilor

Scris de **virgil** Mar 17 Aug 2021, 19:00

Din studiul traiectoriilor putem spune ca acestea se pot imparti in functie de gradul ecuatiilor care le descriu. Astfel vom defini traiectoria de ORDINUL intai ORICE TRAIECTORIE RECTILINIE ce caracterizeaza corpurilor libere care se misca in afara campurilor centrale. In acest caz curbura si torsiunea traiectoriei sunt nule.
Traiectoriile de ORDINUL DOI, sunt traiectoriile descrise de ecuatii de gradul doi, si sunt curbe plane la care torsiunea este totdeauna zero.

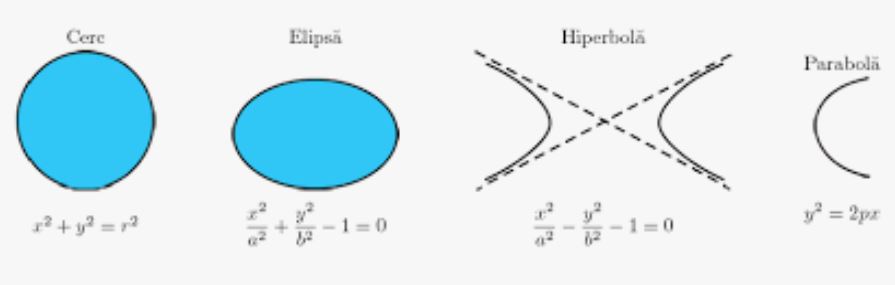
Aceste traiectorii caracterizeaza corpurile care se deplaseaza intr-un camp central static, fie electric sau gravitational.
Traiectoriile de ordinul doi, pot degenera in traiectorii de ordinul intai atunci cand curbura devine zero, devenind o traiectorie dreapta in afara oricaror campuri.
In acest caz curbura traiectoriei poate fi cuprinsa intre zero si infinit, adica de la descrierea unui punct atunci cand raza de curbura este zero, pana la descrierea unei drepte cand raza de curbura este infinita.
Traiectoria de ORDINUL TREI este definita de o ecuatie de gradul trei precum elicea sau orice curba stramba adica tridimensionala.

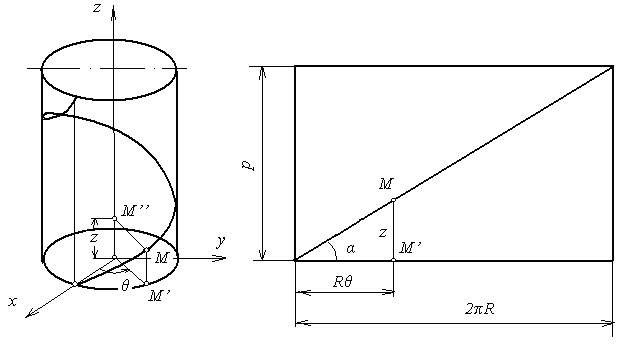
Acest gen de traiectorii se obtin combinand o traiectorie de ordinul doi cu o traiectorie de ordinul intai, adica traiectoriile de ordinul trei se obtin atunci cand corpul aflat intr-un camp central, se deplaseaza odata cu campul pe o alta traiectorie liniara sau curba plana. Exemplu concret, Luna descrie o traiectorie curba plana in jurul Pamantului, iar Pamantul descrie o traiectorie curba plana in jurul Soarelui, din combinatia acestor doua miscari se obtine o traiectorie de ordinul trei, un fel de elice aplatizata in functie de unghiurile planelor celor doua traiectorii ale Lunii si ale Pamatului.
Numai in cazul traiectoriilor tridimensionale putem vorbi despre curbura si torsiune diferite de zero.
Important in definirea acestor traiectorii este ca mai intai sa stabilim unde se afla observatorul.

Scris de **Abel Cavaşi** Mar 17 Aug 2021, 19:07

virgil a scris:Din studiul traiectoriilor putem spune ca acestea se pot imparti in functie de gradul ecuatiilor care le descriu. Astfel vom defini traiectoria de ORDINUL intai ORICE TRAIECTORIE RECTILINIE ce caracterizeaza corpurilor libere care se misca in afara campurilor centrale. In acest caz curbura si torsiunea traiectoriei sunt nule.

Dacă te interesează și părerea mea, ai început destul de prost, cu afirmații false. Știi tu de ce...

Scris de **virgil** Mar 17 Aug 2021, 19:29

Abel Cavaşi a scris:
virgil a scris:Din studiul traiectoriilor putem spune ca acestea se pot imparti in functie de gradul ecuatiilor care le descriu. Astfel vom defini traiectoria de ORDINUL intai ORICE TRAIECTORIE RECTILINIE ce caracterizeaza corpurilor libere care se misca in afara campurilor centrale. In acest caz curbura si torsiunea traiectoriei sunt nule.
Dacă te interesează și părerea mea, ai început destul de prost, cu afirmații false. Știi tu de ce...

Te rog sa detaliezi acest raspuns cu argumente clare ca sa pot si eu sa formulez un raspuns corect. Desigur ma intereseaza parerea critica oricarui coleg dar sa fie fundamentata, pentru ca totdeauna critica este mai constructiva decat lauda.

Scris de **Abel Cavaşi** Mar 17 Aug 2021, 19:49

Nu înțeleg. Să-ți arăt din nou că torsiunea dreptei este nedefinită și că NU ESTE NULĂ?

Scris de **virgil** Mar 17 Aug 2021, 20:40

Abel Cavaşi a scris:Nu înțeleg. Să-ți arăt din nou că torsiunea dreptei este nedefinită și că NU ESTE NULĂ?

Vreau sa-mi demonstrezi care este torsiunea traiectoriilor curbe plane, apoi ne vom referi la torsiunea dreptelor.

Scris de **Abel Cavaşi** Mar 17 Aug 2021, 20:50

virgil a scris:Vreau sa-mi demonstrezi care este torsiunea traiectoriilor curbe plane

Deja începi să schimbi subiectul? Curba plană are torsiunea nulă.

Scris de **gafiteanu** Mier 18 Aug 2021, 04:04

Am studiat cu maxima atentie un fir de ata bine intins si tensionat. Am constatat ca este torsionat. Nu pot aprecia cat de bine era torsionat, daca nu cumva se putea si mai mult torsionat. Va rog sa va dati Dv. cu parerea competenta. Savantii au descoperit ca un fir de paianjen este mai rezistent decat unul de otel de aceeasi grosime, tocmai datorita torsiunii.
Am spart un bec cu filament de wolfram mai special, de inalta tensiune. L-am pus sub microscopul meu electronic, ma rog vorba vine electronic, e cu camera de luat vederi de 14 Megapixeli si ecranul de 24 toli. Am constatat ca este dublu torsionat.
Prin acest filament pot circula electroni. Traiectoria acestora este clar dublu torsionata, iar daca curentul e alternativ, lucrurile se complica. Basca ca si electronii ei insisi sunt torsionati si se misca rasucinduse, deci avem o miscare a electronilor (traiectorie) cel putin triplu torsionata daca nu cumva chiar multiplu.
Minunata-i gradina Ta Doamne Creatorule Suprem...
Doamne, da-ne noua pacatosilor o minte cat mai sucita si rasucita...care sa ne lumineze din interior, precum acest filament sucit si rasucit.
Nu degeaba se zice celor cu idei ca le fileaza o lampa... E o vorba a prostilor, cand vad pe unul mai luminat...

Scris de **virgil_48** Mier 18 Aug 2021, 07:57

Torsionarea aceasta a firelor se face pe criterii de necesitate
tehnologica. Firul de ață ca sa nu se destrame, filamentele si
rezistentele pentru ca lungimea totală să fie redusă.
Am vazut si becuri cu filamentul drept !
Poate mai sunt si alte criterii, legate de eficienta. Un tirbușon
drept, nu functioneaza. Armele cu țevi ghintuite sunt superioare.
Torsionarea aceasta a unor fire, obiecte, nu are nici o legatura
cu miscarea elicoidala. Cel mult, ca sa dea idei de cercetare.

Scris de **virgil** Mier 18 Aug 2021, 08:07

Abel Cavaşi a scris:
virgil a scris:Vreau sa-mi demonstrezi care este torsiunea traiectoriilor curbe plane
Deja începi să schimbi subiectul? Curba plană are torsiunea nulă.

Deci orice curba plana are torsiunea nula, pana aici suntem de acord. Dar stii ca orice curba plana cu raza infinita degenereaza intr-o dreapta care va avea torsiunea zero si curbura zero.
quod erat demonstrandum !
Multumesc Abel pentru ajutor.

Scris de **virgil_48** Mier 18 Aug 2021, 08:26

Abel Cavaşi a scris:
virgil a scris:Vreau sa-mi demonstrezi care este torsiunea traiectoriilor curbe plane
Deja începi să schimbi subiectul? Curba plană are torsiunea nulă.

Pai dreapta, fiindca este plana, are torsiunea nedeterminata(asa
sustine Abel !) iar o curba plana are torsiunea nula ? Adica dece
nu este tot nedeterminata ?
Curbura plana face ca torsiunea sa nu mai fie nedeterminata si
sa devina nula ? Adica curbarea unei drepte ii determina torsiunea ?
Incercarea de a rasturna mecanica cu ajutorul a doua atribute,
nula/ nedeterminata folosite dupa nevoie, nu poate avea
sanse. Sunt necesare argumente mai solide.
P.S Dialogul din citat, in care un interlocutor vorbeste despre
mecanica si altul despre geometrie, nu poate da rezultate.

Scris de **Abel Cavaşi** Mier 18 Aug 2021, 09:30

virgil a scris:Deci orice curba plana are torsiunea nula, pana aici suntem de acord.

Desigur. Nici n-am susținut niciodată altfel. În plus, nu are legătură cu faptul că dreapta are torsiunea nedeterminată.

Dar stii ca orice curba plana cu raza infinita degenereaza intr-o dreapta care va avea torsiunea zero si curbura zero.
quod erat demonstrandum !
Multumesc Abel pentru ajutor.

Ei, ce repede ai fugit! Crezi că scapi așa ușor? Cum adică? Ai mai spus:

orice curba plana cu raza infinita degenereaza intr-o dreapta

Nu chiar orice curbă plană, dar știu ce vrei să zici. Să zicem, un cerc. Un cerc este o curbă plană, DAR NUMAI PÂNĂ ARE RAZA FINITĂ. În momentul în care raza cercului devine infinită, el nu mai este o curbă plană, pentru că atunci curbura lui se anulează, iar torsiunea devine nedeterminată. Așa că, ai sărit repede la infinit, unde adevărul afirmațiilor tale pică.

Așadar, afirmația ta

degenereaza intr-o dreapta care va avea torsiunea zero

este falsă! Torsiunea dreptei este și va rămâne nedefinită.

Iar dacă mai vii cu chestii de genul:

quod erat demonstrandum !
Multumesc Abel pentru ajutor.

nu te mai aștepta la discuții cu mine.

Scris de **Abel Cavaşi** Mier 18 Aug 2021, 09:35

virgil_48 a scris:Pai dreapta, fiindca este plana, are torsiunea nedeterminata(asa
sustine Abel !)

Unde am spus eu că dreapta este plană?

iar o curba plana are torsiunea nula ? Adica dece
nu este tot nedeterminata ?

Înainte de a te băga în discuții de acest gen apucă-te de studiu.

Incercarea de a rasturna mecanica cu ajutorul a doua atribute,
nula/ nedeterminata folosite dupa nevoie, nu poate avea
sanse. Sunt necesare argumente mai solide.

Ai tu vreun argument solid pentru această afirmație? Sau este doar o vorbă în vânt?

Scris de **virgil_48** Mier 18 Aug 2021, 10:39

Abel Cavaşi a scris:
virgil_48 a scris:Pai dreapta, fiindca este plana, are torsiunea nedeterminata(asa
sustine Abel !)
Unde am spus eu că dreapta este plană?

Nu este nevoie sa spui asa ceva. Stie oricine. Este adevarat numai
ce spui tu ?

iar o curba plana are torsiunea nula ? Adica dece
nu este tot nedeterminata ?
Înainte de a te băga în discuții de acest gen apucă-te de studiu.

Si daca nu mai particip, crezi ca sustinerile tale devin adevarate ?
Mi-ai recomandat asta de prea multe ori, ca sa nu-ti
recomand si eu prieteneste un manual de fizica elementara. Si
putin discernamant in gandire.

Incercarea de a rasturna mecanica cu ajutorul a doua atribute,
nula/ nedeterminata folosite dupa nevoie, nu poate avea
sanse. Sunt necesare argumente mai solide.
Ai tu vreun argument solid pentru această afirmație? Sau este doar o vorbă în vânt?

Eu am nevoie de argument solid pentru o afirmatie de bun simt,
iar tu poti rasturna mecanica cu doua vorbe utilizate arbitrar ?

Scris de **virgil** Mier 18 Aug 2021, 13:24

Abel Cavaşi a scris:
virgil a scris:Deci orice curba plana are torsiunea nula, pana aici suntem de acord.
Desigur. Nici n-am susținut niciodată altfel. În plus, nu are legătură cu faptul că dreapta are torsiunea nedeterminată.

Dar stii ca orice curba plana cu raza infinita degenereaza intr-o dreapta care va avea torsiunea zero si curbura zero.
quod erat demonstrandum !
Multumesc Abel pentru ajutor.
Ei, ce repede ai fugit! Crezi că scapi așa ușor? Cum adică? Ai mai spus:
orice curba plana cu raza infinita degenereaza intr-o dreapta
Nu chiar orice curbă plană, dar știu ce vrei să zici.
Să zicem, un cerc. Un cerc este o curbă plană, DAR NUMAI PÂNĂ ARE RAZA FINITĂ. În momentul în care raza cercului devine infinită, el nu mai este o curbă plană, pentru că atunci curbura lui se anulează, iar torsiunea devine nedeterminată. Așa că, ai sărit repede la infinit, unde adevărul afirmațiilor tale pică.

Virgil;
Cercul, este o curba plana inchisa, si oricat ii cresti raza tot cerc ramane. Eu ma refer la o curba plana deschisa precum un arc de cerc, sau o parabola pentru care la limita se reduce curbura la zero, si torsiunea ramane nemodificata adica tot zero.

Așadar, afirmația ta
degenereaza intr-o dreapta care va avea torsiunea zero
este falsă! Torsiunea dreptei este și va rămâne nedefinită.
Virgil;
Mai ramane sa demonstrezi din ce fel de curba obtii dreapta.

Scris de **Abel Cavaşi** Mier 18 Aug 2021, 14:20

virgil a scris:la limita se reduce curbura la zero, si torsiunea ramane nemodificata adica tot zero.

Fals!

Mai ramane sa demonstrezi din ce fel de curba obtii dreapta.

De când am ajuns eu să fiu nevoit să-ți demonstrez ce este o dreaptă? Pune mâna pe carte și învață!

Scris de **virgil_48** Mier 18 Aug 2021, 16:45

A bate pasul pe loc cu clasificarea traiectoriilor atunci cand este
vorba de miscarea elicoidala, este inutil si contraproductiv.
Este suficient sa o clasifici ca o miscare nelibera, fortata,
care are loc numai sub influenta unor factorilor exteriori. Adica
cei de mediu/naturali sau propulsia/artificiali. Cine ar sustine
altceva, trebuie in primul rand sa indice unde are loc miscarea
elicoidala/libera in mod natural. Fara acest prim pas, totul este
vorba lunga si pierdere de timp. Dece sa intri in teorii asupra
unei miscari despre care nu poti arata ca exista in realitate?
Negarea miscarii rectilinii incearca sa autentifice miscarea
elicoidala prin eliminarea celei concurente, recunoscute.
Asadar, dece sa vorbim discutii ? Vom afla si noi un exemplu
convingator de miscare elicoidala/libera/naturala/observabila,
a unui corp. Fara formule, pretexte, eschive, trimiteri, nervi,
jigniri, ascunderea in microcosmos, etc. Un exemplu frumos !
Suspansul a durat prea mult pe acest forum! Riscam sa nu il
mai aflam niciodata daca exista(acel exemplu).

Scris de **virgil** Mier 18 Aug 2021, 18:37

Abel Cavaşi a scris:
virgil a scris:la limita se reduce curbura la zero, si torsiunea ramane nemodificata adica tot zero.
Fals!

Mai ramane sa demonstrezi din ce fel de curba obtii dreapta.
De când am ajuns eu să fiu nevoit să-ți demonstrez ce este o dreaptă? Pune mâna pe carte și învață!

Acesta este un raspuns tipic pentru tine. Cand un coleg iti cere sa demonstrezi ceva prin care sa-ti clarifici afirmatiile, chiar trebuie s-o faci, daca nu afirmatiile tale raman nefondate.

Scris de Continut sponsorizat

Clasificarea traiectoriilor

Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor

Re: Clasificarea traiectoriilor