Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Forever_Man Ieri la 22:56
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la No_name în How Self-Reference Builds the World - articol nou
( 1 )
» Mesaj de la CAdi în Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
( 1 )
» Mesaj de la No_name în Ce anume "generează" legile fizice?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12458) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Spune şi altora
Cine este conectat?
În total sunt 21 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 21 Vizitatori :: 2 Motoare de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Teoria relativității restrânse - Formule - Întrebări
+3
gafiteanu
Razvan
Dacu
7 participanți
Pagina 1 din 2
Pagina 1 din 2 • 1, 2 
 Teoria relativității restrânse - Formule - Întrebări
Teoria relativității restrânse - Formule - Întrebări
Care este formula de calcul a densității relativiste a unui corp?
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Densitatea relativistă exprimată în funcţie de masa iniţială m_0 şi volumul iniţial V_0 este:

unde gamma este factorul Lorentz: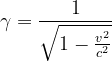
unde gamma este factorul Lorentz:
_________________
Eşti inteligent atunci când crezi doar jumătate din ceea ce afli; eşti înţelept atunci când ştii care jumătate!

Razvan- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 6183




Puncte : 33836
Data de inscriere : 18/03/2011
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Care este forma relativistă a unui corp (care în stare de repaus are forma unui paralelipiped dreptunghic) ce se deplasează pe direcția diagonalei lui și care este în acest caz densitatea relativistă a acestui corp?Razvan a scris:Densitatea relativistă exprimată în funcţie de masa iniţială m_0 şi volumul iniţial V_0 este:
unde gamma este factorul Lorentz:
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Din moment ce contracţia lungimii se produce pe direcţia de deplasare, în cazul de faţă contracţia va avea loc pe direcţia diagonalei.
Paralelipipedul va apare ca deformat pentru un observator extern. Densitatea lui va fi cea dată prin formula de mai sus, după ce determini volumul figurii geometrice rezultante.
Paralelipipedul va apare ca deformat pentru un observator extern. Densitatea lui va fi cea dată prin formula de mai sus, după ce determini volumul figurii geometrice rezultante.
_________________
Eşti inteligent atunci când crezi doar jumătate din ceea ce afli; eşti înţelept atunci când ştii care jumătate!

Razvan- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 6183




Puncte : 33836
Data de inscriere : 18/03/2011
virgil apreciază acest mesaj
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Atunci cand o cuanta isi creste energia dintrun anumit motiv, densitatea ei creste si isi micsoreaza volumul. Ca urmare si propria frecventa de oscilatie-pulsatie creste, iar lungimea de unda se micsoreaza.
Cum isi creste densitatea si isi micsoreaza volumul ? Aici e aici, trebuie o mare discutie. Probabil ca densitatea unei cuante nu este aceeasi in tot volumul ei. O extremitate e cu densitate mica iar alta cu densitate mare.
De exemplu un foton din zona luminoasa este mult mai "pufos" decat unul ultraviolet, iar aceste e mai putin dens decat unul X=Roentgen si cel mai dens ar trebui sa fie fotonul=radiatia EM de tip Gamma, care are cea mai mare frecventa. Lungimea de unda difera foarte mult in cazul fotonilor si cuantelor, de la km in cazul undelor radio pana la mult sub dimensiunea electronilor sau protonilor, care este 10^-15m.
Stiti ce este in realitate aceasta lungime de unda ? Puteti sa fiti siguri ca este mai mare chiar decat dimensiunea cuantei.
Un parametru important in cazul cuantelor ar trebui sa fie raportul dintre lungimea cuantei pe directia de miscare si diametrul ei. Cuanta are lungime si latime, nu este un gogoloi. Mai are inca multe alte aspecte forma cuantei. Cuanta nu este chiar ca un glont, are cap, gura, trup, coada, intestin, anus, sex, etc...
„Ce-ți pasă ție, chip de lut,..." zise Eminescu... Si Dumnezeu pocni din degete si dadu in Chaos impulsul initial si zise: "Fiat lux" si lumina se facu...(Facerea, Ziua intai )...
Cum isi creste densitatea si isi micsoreaza volumul ? Aici e aici, trebuie o mare discutie. Probabil ca densitatea unei cuante nu este aceeasi in tot volumul ei. O extremitate e cu densitate mica iar alta cu densitate mare.
De exemplu un foton din zona luminoasa este mult mai "pufos" decat unul ultraviolet, iar aceste e mai putin dens decat unul X=Roentgen si cel mai dens ar trebui sa fie fotonul=radiatia EM de tip Gamma, care are cea mai mare frecventa. Lungimea de unda difera foarte mult in cazul fotonilor si cuantelor, de la km in cazul undelor radio pana la mult sub dimensiunea electronilor sau protonilor, care este 10^-15m.
Stiti ce este in realitate aceasta lungime de unda ? Puteti sa fiti siguri ca este mai mare chiar decat dimensiunea cuantei.
Un parametru important in cazul cuantelor ar trebui sa fie raportul dintre lungimea cuantei pe directia de miscare si diametrul ei. Cuanta are lungime si latime, nu este un gogoloi. Mai are inca multe alte aspecte forma cuantei. Cuanta nu este chiar ca un glont, are cap, gura, trup, coada, intestin, anus, sex, etc...
„Ce-ți pasă ție, chip de lut,..." zise Eminescu... Si Dumnezeu pocni din degete si dadu in Chaos impulsul initial si zise: "Fiat lux" si lumina se facu...(Facerea, Ziua intai )...
_________________
“Toată lumea se plânge că nu are memorie, dar nimeni nu se vaită că nu are logică.” (La Rochefoucauld)
gafiteanu- Foarte activ

- Mulţumit de forum : Prenume : Vaxile




Numarul mesajelor : 7617
Puncte : 36100
Data de inscriere : 13/06/2011
Obiective curente : 0)-Fondator "Asociatia Fostilor Cercetatori Stiintifici".
1)-Stiinta camuflata in bascalie pentru tonti. Imi perfectionez stilul bascalios.
2)-Să-mi schimb sexul. Transplant cu altul mai vârtos. Si care să stie si carte.
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Reformulez întrebarea din prima mea postare:Razvan a scris:Din moment ce contracţia lungimii se produce pe direcţia de deplasare, în cazul de faţă contracţia va avea loc pe direcţia diagonalei.
Paralelipipedul va apare ca deformat pentru un observator extern. Densitatea lui va fi cea dată prin formula de mai sus, după ce determini volumul figurii geometrice rezultante.
Care este forma relativistă a unui corp (care în stare de repaus are forma unui paralelipiped dreptunghic) ce se deplasează pe o direcție paralelă cu una din laturile sale și care este în acest caz densitatea relativistă a acestui corp?
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Depinde de locul unde se afla cel care face masuratorile. Daca te afli in acel cub bineinteles ca veZi si masori toate laturile egale ale cubului. Daca te afli intr-un sistem de referinta din afara cubului si te deplasezi cu viteza apropiata de a luminii ai sa vezi in loc de cub o prisma cu latura mai mica pe directia de deplasare. Deci cubul apare comprimat, iar masa relativista creste, deci densitatea relativista este produsul dintre densitatea ro zero cu patratul factorului relativistic notat cu gama.Dacu a scris:Reformulez întrebarea din prima mea postare:Razvan a scris:Din moment ce contracţia lungimii se produce pe direcţia de deplasare, în cazul de faţă contracţia va avea loc pe direcţia diagonalei.
Paralelipipedul va apare ca deformat pentru un observator extern. Densitatea lui va fi cea dată prin formula de mai sus, după ce determini volumul figurii geometrice rezultante.
Care este forma relativistă a unui corp (care în stare de repaus are forma unui paralelipiped dreptunghic) ce se deplasează pe o direcție paralelă cu una din laturile sale și care este în acest caz densitatea relativistă a acestui corp?
In cazul deplasarii paralelipipedului dreptunghic daca aceasta se deplasaza pe directia laturii celei mai lungi, atunci acesta va fi vazut din alt siatem de referinta cu acea latura scurtata adica mai apropiat de forma cubului.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Eu vorbesc despre un paralelipiped și acesta se deplasează cu viteza v iar măsurătorile se fac de cineva care este in repaus si deci repet:virgil a scris:Depinde de locul unde se afla cel care face masuratorile. Daca te afli in acel cub bineinteles ca veZi si masori toate laturile egale ale cubului. Daca te afli intr-un sistem de referinta din afara cubului si te deplasezi cu viteza apropiata de a luminii ai sa vezi in loc de cub o prisma cu latura mai mica pe directia de deplasare. Deci cubul apare comprimat, iar masa relativista creste, deci densitatea relativista este produsul dintre densitatea ro zero cu patratul factorului relativistic notat cu gama.Dacu a scris:Reformulez întrebarea din prima mea postare:Razvan a scris:Din moment ce contracţia lungimii se produce pe direcţia de deplasare, în cazul de faţă contracţia va avea loc pe direcţia diagonalei.
Paralelipipedul va apare ca deformat pentru un observator extern. Densitatea lui va fi cea dată prin formula de mai sus, după ce determini volumul figurii geometrice rezultante.
Care este forma relativistă a unui corp (care în stare de repaus are forma unui paralelipiped dreptunghic) ce se deplasează pe o direcție paralelă cu una din laturile sale și care este în acest caz densitatea relativistă a acestui corp?
In cazul deplasarii paralelipipedului dreptunghic daca aceasta se deplasaza pe directia laturii celei mai lungi, atunci acesta va fi vazut din alt siatem de referinta cu acea latura scurtata adica mai apropiat de forma cubului.
Care este forma relativistă a unui corp (care în stare de repaus are forma unui paralelipiped dreptunghic) ce se deplasează pe o direcție paralelă cu una din laturile sale și care este în acest caz densitatea relativistă a acestui corp?
Altfel pusă întrebarea ar fi:
Care sunt dimensiunile paralelipipedului în acest caz?
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Eu am raspuns cam asa;Dacu a scris:Eu vorbesc despre un paralelipiped și acesta se deplasează cu viteza v iar măsurătorile se fac de cineva care este in repaus si deci repet:virgil a scris:Depinde de locul unde se afla cel care face masuratorile. Daca te afli in acel cub bineinteles ca veZi si masori toate laturile egale ale cubului. Daca te afli intr-un sistem de referinta din afara cubului si te deplasezi cu viteza apropiata de a luminii ai sa vezi in loc de cub o prisma cu latura mai mica pe directia de deplasare. Deci cubul apare comprimat, iar masa relativista creste, deci densitatea relativista este produsul dintre densitatea ro zero cu patratul factorului relativistic notat cu gama.Dacu a scris:
Reformulez întrebarea din prima mea postare:
Care este forma relativistă a unui corp (care în stare de repaus are forma unui paralelipiped dreptunghic) ce se deplasează pe o direcție paralelă cu una din laturile sale și care este în acest caz densitatea relativistă a acestui corp?
In cazul deplasarii paralelipipedului dreptunghic daca aceasta se deplasaza pe directia laturii celei mai lungi, atunci acesta va fi vazut din alt siatem de referinta cu acea latura scurtata adica mai apropiat de forma cubului.
Care este forma relativistă a unui corp (care în stare de repaus are forma unui paralelipiped dreptunghic) ce se deplasează pe o direcție paralelă cu una din laturile sale și care este în acest caz densitatea relativistă a acestui corp?
Altfel pusă întrebarea ar fi:
Care sunt dimensiunile paralelipipedului în acest caz?
In cazul deplasarii cu viteze apropiate de viteza luminii a paralelipipedului dreptunghic, daca aceasta se deplasaza pe directia laturii celei mai lungi, atunci acesta va fi vazut din alt sistem de referinta aflat in repaus ca avand latura scurtata adica mai apropiat de forma cubului.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Ca sa ceri dimensiunile trebuie sa dai viteza paralelipipedului si dimensiunile lui si directia, Dacule.Dacu a scris:
Eu vorbesc despre un paralelipiped și acesta se deplasează cu viteza v iar măsurătorile se fac de cineva care este in repaus si deci repet:
Care este forma relativistă a unui corp (care în stare de repaus are forma unui paralelipiped dreptunghic) ce se deplasează pe o direcție paralelă cu una din laturile sale și care este în acest caz densitatea relativistă a acestui corp?
Altfel pusă întrebarea ar fi:
Care sunt dimensiunile paralelipipedului în acest caz?
CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12397




Puncte : 59038
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
.......................
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
...............................
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Nu-nțeleg ce vrei să spui!virgil a scris:Eu am raspuns cam asa;Dacu a scris:Eu vorbesc despre un paralelipiped și acesta se deplasează cu viteza v iar măsurătorile se fac de cineva care este in repaus si deci repet:virgil a scris:
Depinde de locul unde se afla cel care face masuratorile. Daca te afli in acel cub bineinteles ca veZi si masori toate laturile egale ale cubului. Daca te afli intr-un sistem de referinta din afara cubului si te deplasezi cu viteza apropiata de a luminii ai sa vezi in loc de cub o prisma cu latura mai mica pe directia de deplasare. Deci cubul apare comprimat, iar masa relativista creste, deci densitatea relativista este produsul dintre densitatea ro zero cu patratul factorului relativistic notat cu gama.
In cazul deplasarii paralelipipedului dreptunghic daca aceasta se deplasaza pe directia laturii celei mai lungi, atunci acesta va fi vazut din alt siatem de referinta cu acea latura scurtata adica mai apropiat de forma cubului.
Care este forma relativistă a unui corp (care în stare de repaus are forma unui paralelipiped dreptunghic) ce se deplasează pe o direcție paralelă cu una din laturile sale și care este în acest caz densitatea relativistă a acestui corp?
Altfel pusă întrebarea ar fi:
Care sunt dimensiunile paralelipipedului în acest caz?
In cazul deplasarii cu viteze apropiate de viteza luminii a paralelipipedului dreptunghic, daca aceasta se deplasaza pe directia laturii celei mai lungi, atunci acesta va fi vazut din alt sistem de referinta aflat in repaus ca avand latura scurtata adica mai apropiat de forma cubului.
Să înțrleg că în cazul în care laturile paralelipipedului aflat în repaus sunt [b]x
.............................................
De ce nu apare tot mesajul?
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
De ce nu apare tot mesajul meu?S-o fi supărat Abel pe mine?!?!!!CAdi a scris:Ca sa ceri dimensiunile trebuie sa dai viteza paralelipipedului si dimensiunile lui si directia, Dacule.Dacu a scris:
Eu vorbesc despre un paralelipiped și acesta se deplasează cu viteza v iar măsurătorile se fac de cineva care este in repaus si deci repet:
Care este forma relativistă a unui corp (care în stare de repaus are forma unui paralelipiped dreptunghic) ce se deplasează pe o direcție paralelă cu una din laturile sale și care este în acest caz densitatea relativistă a acestui corp?
Altfel pusă întrebarea ar fi:
Care sunt dimensiunile paralelipipedului în acest caz?
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
N-ar trebui să crezi asta despre mine. Dacă am motive serioase să fac așa ceva, îți spun.De ce nu apare tot mesajul meu?S-o fi supărat Abel pe mine?!?!!!
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
........................................................virgil a scris:Eu am raspuns cam asa;Dacu a scris:Eu vorbesc despre un paralelipiped și acesta se deplasează cu viteza v iar măsurătorile se fac de cineva care este in repaus si deci repet:virgil a scris:
Depinde de locul unde se afla cel care face masuratorile. Daca te afli in acel cub bineinteles ca veZi si masori toate laturile egale ale cubului. Daca te afli intr-un sistem de referinta din afara cubului si te deplasezi cu viteza apropiata de a luminii ai sa vezi in loc de cub o prisma cu latura mai mica pe directia de deplasare. Deci cubul apare comprimat, iar masa relativista creste, deci densitatea relativista este produsul dintre densitatea ro zero cu patratul factorului relativistic notat cu gama.
In cazul deplasarii paralelipipedului dreptunghic daca aceasta se deplasaza pe directia laturii celei mai lungi, atunci acesta va fi vazut din alt siatem de referinta cu acea latura scurtata adica mai apropiat de forma cubului.
Care este forma relativistă a unui corp (care în stare de repaus are forma unui paralelipiped dreptunghic) ce se deplasează pe o direcție paralelă cu una din laturile sale și care este în acest caz densitatea relativistă a acestui corp?
Altfel pusă întrebarea ar fi:
Care sunt dimensiunile paralelipipedului în acest caz?
In cazul deplasarii cu viteze apropiate de viteza luminii a paralelipipedului dreptunghic, daca aceasta se deplasaza pe directia laturii celei mai lungi, atunci acesta va fi vazut din alt sistem de referinta aflat in repaus ca avand latura scurtata adica mai apropiat de forma cubului.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Nu-nțeleg ce vrei să spui!Abel Cavaşi a scris:N-ar trebui să crezi asta despre mine. Dacă am motive serioase să fac așa ceva, îți spun.De ce nu apare tot mesajul meu?S-o fi supărat Abel pe mine?!?!!!

Să înțrleg că în cazul în care laturile paralelipipedului aflat în repaus sunt [b]x
Ce se-ntâmplă???????!!!!!!!
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
"virgil",
Să înțrleg că în cazul în care laturile paralelipipedului aflat în repaus sunt [b]x ........................................................................
Să înțrleg că în cazul în care laturile paralelipipedului aflat în repaus sunt [b]x ........................................................................
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Aceiași eroare apare la toate subiectele de pe forum chiar daca scriu și pe MP......Ce se întâmplă?Abel Cavaşi a scris:N-ar trebui să crezi asta despre mine. Dacă am motive serioase să fac așa ceva, îți spun.De ce nu apare tot mesajul meu?S-o fi supărat Abel pe mine?!?!!!

Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Dacu a scris:"virgil",
Să înțrleg că în cazul în care laturile paralelipipedului aflat în repaus sunt [b]x ........................................................................
Ce-i asa de complcat, daca deplasarea paralelipipedului se face pe directia laturii lungi, tu aflat in repaus o vezi ceva mai scurta in functie de viteza cu care se deplaseaza.
PS; Cred ca ai ceva la tastatura, daca ai pisica intreab-o pe ea.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Dacu a scris:Aceiași eroare apare la toate subiectele de pe forum chiar daca scriu și pe MP......Ce se întâmplă?Abel Cavaşi a scris:N-ar trebui să crezi asta despre mine. Dacă am motive serioase să fac așa ceva, îți spun.De ce nu apare tot mesajul meu?S-o fi supărat Abel pe mine?!?!!!

Dacu, cred ca s-a stricat editarea de formule.
Cu privire la paralelipipedul care se deplaseaza cu o viteza apropiata de viteza luminii are loc o contractie a lungimii acestuia ; obiectul se aplatizeaza...
Aceasta se intampla deoarece are loc o masuratoare in alt sistem de referinta iar obiectul este in miscare cu viteze relativiste si deci apare un timp dt la masuratoare.
Paralelipipedul se ,,contracta " pe lungime cu relatia :
x=,,gama"(x1-v.t) celelalte dimensiuni raman neschimbate.
y=y1
z=z1
unde ,,gama"=1/sqrt(1-v^2/c^2) este factorul de transformare Lorentz.
sau dv= ,,gama"((dx1)-v.dt) ca sa vezi cum intra dt in relatie.
CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12397




Puncte : 59038
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Dacă viteza paralelipipedului tinde la viteza luminii, atunci care este valoarea volumului relativist al acestuia?virgil a scris:Eu am raspuns cam asa;Dacu a scris:Eu vorbesc despre un paralelipiped și acesta se deplasează cu viteza v iar măsurătorile se fac de cineva care este in repaus si deci repet:virgil a scris:
Depinde de locul unde se afla cel care face masuratorile. Daca te afli in acel cub bineinteles ca veZi si masori toate laturile egale ale cubului. Daca te afli intr-un sistem de referinta din afara cubului si te deplasezi cu viteza apropiata de a luminii ai sa vezi in loc de cub o prisma cu latura mai mica pe directia de deplasare. Deci cubul apare comprimat, iar masa relativista creste, deci densitatea relativista este produsul dintre densitatea ro zero cu patratul factorului relativistic notat cu gama.
In cazul deplasarii paralelipipedului dreptunghic daca aceasta se deplasaza pe directia laturii celei mai lungi, atunci acesta va fi vazut din alt siatem de referinta cu acea latura scurtata adica mai apropiat de forma cubului.
Care este forma relativistă a unui corp (care în stare de repaus are forma unui paralelipiped dreptunghic) ce se deplasează pe o direcție paralelă cu una din laturile sale și care este în acest caz densitatea relativistă a acestui corp?
Altfel pusă întrebarea ar fi:
Care sunt dimensiunile paralelipipedului în acest caz?
In cazul deplasarii cu viteze apropiate de viteza luminii a paralelipipedului dreptunghic, daca aceasta se deplasaza pe directia laturii celei mai lungi, atunci acesta va fi vazut din alt sistem de referinta aflat in repaus ca avand latura scurtata adica mai apropiat de forma cubului.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
_________________
Eşti inteligent atunci când crezi doar jumătate din ceea ce afli; eşti înţelept atunci când ştii care jumătate!

Razvan- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 6183




Puncte : 33836
Data de inscriere : 18/03/2011
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Formulele pentru x, y, z scrise de dumneata ne arată că nu este vorba despre o aplatizare deoarece aplatizarea presupune o turtire și deci y1 trebuie să fie mai mare ca y și z1 trebuie să fie mai mare ca z.CAdi a scris:Dacu a scris:Aceiași eroare apare la toate subiectele de pe forum chiar daca scriu și pe MP......Ce se întâmplă?Abel Cavaşi a scris:
N-ar trebui să crezi asta despre mine. Dacă am motive serioase să fac așa ceva, îți spun.
Dacu, cred ca s-a stricat editarea de formule.
Cu privire la paralelipipedul care se deplaseaza cu o viteza apropiata de viteza luminii are loc o contractie a lungimii acestuia ; obiectul se aplatizeaza...
Aceasta se intampla deoarece are loc o masuratoare in alt sistem de referinta iar obiectul este in miscare cu viteze relativiste si deci apare un timp dt la masuratoare.
Paralelipipedul se ,,contracta " pe lungime cu relatia :
x=,,gama"(x1-v.t) celelalte dimensiuni raman neschimbate.
y=y1
z=z1
unde ,,gama"=1/sqrt(1-v^2/c^2) este factorul de transformare Lorentz.
sau dv= ,,gama"((dx1)-v.dt) ca sa vezi cum intra dt in relatie.
În cazul aplatizării, dacă viteza paralelipipedului tinde la viteza luminii atunci ar trebui ca x1 să tindă la zero iar y1 și z1 să tindă la infinit ceea ce ar conduce la faptul că volumul paralelipipedului ar fi egal cu infinit înmulțit cu infinit înmulțit cu zero și asta din punct de vedere matematic înseamnă o nedeterminare.Deoarece volumul relativist al paralelipipedului nu poate fi determinat atunci nu putem determina nici densitatea relativistă a acelui paralelipiped și deci nu putem calcula nici masa relativistă a acestuia pentru ca ajungem la 2 formule de calcul ale masei relativiste care nu sunt identice...
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Da , nu este ales prea fericit termenul. Nu este o aplatizare este o ,,contractie a lungimii" datorita diferentei de timp de masura in diferite SR , asa cum se explica in Wikipedia :
https://ro.wikipedia.org/wiki/Teoria_relativității_restrânse
citat : Contracția Lorentz — dimensiunile (de exemplu lungimea) unui obiect măsurate de un observator pot fi mai mici decât rezultatele acelorași măsurători efectuate de un alt observator
https://ro.wikipedia.org/wiki/Teoria_relativității_restrânse
citat : Contracția Lorentz — dimensiunile (de exemplu lungimea) unui obiect măsurate de un observator pot fi mai mici decât rezultatele acelorași măsurători efectuate de un alt observator
CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12397




Puncte : 59038
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Dacă viteza paralelipipedului tinde la viteza luminii,atunci la ce valoare tinde volumul relativist al paralelipipedului?Razvan a scris:
Ultima editare efectuata de catre Dacu in Mier 02 Feb 2022, 08:41, editata de 2 ori
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Vrei să spui că y și z nu se modifică?Dacă da, atunci la ce valoare va tinde volumul relativist al paralelipipedului în cazul în care viteza acestuia tinde la viteza luminii?CAdi a scris:Da , nu este ales prea fericit termenul. Nu este o aplatizare este o ,,contractie a lungimii" datorita diferentei de timp de masura in diferite SR , asa cum se explica in Wikipedia :
https://ro.wikipedia.org/wiki/Teoria_relativității_restrânse
citat : Contracția Lorentz — dimensiunile (de exemplu lungimea) unui obiect măsurate de un observator pot fi mai mici decât rezultatele acelorași măsurători efectuate de un alt observator
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Volumul relativist il gasesti cu relatia data de Razvan.
Sa-ti explic cum vad eu de ce y,z nu se modifica si se modifica numai x :
Daca avem acest paralelipiped trebuie sa masuram capetele paralelipipedului care intr-un sistem de referinta legat de acesta S au latura x
In momentul cand faci prima masuratoare in timpul t1 in S , masori suprafata y.z si lungimea x ,apoi in timpul t2 in S' masori aceeasi suprafata y.z dar intre timp paralelipipedul s-a deplasat cu o
viteza apropiata de viteza luminii si lungimea x s-a micsorat , apare timpul dt1. Treaba aceasta se datoreste sistemelor de referinta in care se gaseste obiectul si din care se face masuratoarea ;
Presupunerea pleaca de la faptul ca un al doilea sistem de referință S' are axele spatiale si un ceas ce coincide exact cu ale lui S in care se gaseste paralelipipedul la momentul zero,
dar care se misca cu o viteza constanta v în raport cu S' in jurul axei x.
Gama este factorul de transformare Lorentz:
,,gama"=1/sqrt(1-v^2/c^2) este factorul de transformare Lorentz.
Deci masuratoarea in cele 2 SR este legata de dilatarea temporara :
Aceasta arata ca durata de timp dt intre doua batai ale ceasului, pentru sistemul in miscare S este mai mare decat durata de timp dt dintre aceleasi batai masurate in sistemul in care ceasul este in repaus S'
pe Terra de exemplu.
adica dt1=,,gama" dt
In mod corespunzator la contractia lungimii :
dx1= dx/,,gama"
Sa-ti explic cum vad eu de ce y,z nu se modifica si se modifica numai x :
Daca avem acest paralelipiped trebuie sa masuram capetele paralelipipedului care intr-un sistem de referinta legat de acesta S au latura x
In momentul cand faci prima masuratoare in timpul t1 in S , masori suprafata y.z si lungimea x ,apoi in timpul t2 in S' masori aceeasi suprafata y.z dar intre timp paralelipipedul s-a deplasat cu o
viteza apropiata de viteza luminii si lungimea x s-a micsorat , apare timpul dt1. Treaba aceasta se datoreste sistemelor de referinta in care se gaseste obiectul si din care se face masuratoarea ;
Presupunerea pleaca de la faptul ca un al doilea sistem de referință S' are axele spatiale si un ceas ce coincide exact cu ale lui S in care se gaseste paralelipipedul la momentul zero,
dar care se misca cu o viteza constanta v în raport cu S' in jurul axei x.
Gama este factorul de transformare Lorentz:
,,gama"=1/sqrt(1-v^2/c^2) este factorul de transformare Lorentz.
Deci masuratoarea in cele 2 SR este legata de dilatarea temporara :
Aceasta arata ca durata de timp dt intre doua batai ale ceasului, pentru sistemul in miscare S este mai mare decat durata de timp dt dintre aceleasi batai masurate in sistemul in care ceasul este in repaus S'
pe Terra de exemplu.
adica dt1=,,gama" dt
In mod corespunzator la contractia lungimii :
dx1= dx/,,gama"
CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12397




Puncte : 59038
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Dacă volumul relațivist al paralelipipedului tinde la zero atunci asta ar însemna că acest paralelipiped devine inperceptibil pentru ochii observatorului, ceea ce nu este totuna că masa acelui paralelipiped ar tinde la înfinit dar cu siguranță impulsul acestuia ar fi egal cu produsul dintre masa lui în repaus și viteza luminii, atâta tot și nimic altceva.Este aberant să se tragă concluzia că masa acelui paralelipiped ar tinde la îfinit dacă viteza acestuia tinde la infinit!CAdi a scris:Volumul relativist il gasesti cu relatia data de Razvan.
Sa-ti explic cum vad eu de ce y,z nu se modifica si se modifica numai x :
Daca avem acest paralelipiped trebuie sa masuram capetele paralelipipedului care intr-un sistem de referinta legat de acesta S au latura x
In momentul cand faci prima masuratoare in timpul t1 in S , masori suprafata y.z si lungimea x ,apoi in timpul t2 in S' masori aceeasi suprafata y.z dar intre timp paralelipipedul s-a deplasat cu o
viteza apropiata de viteza luminii si lungimea x s-a micsorat , apare timpul dt1. Treaba aceasta se datoreste sistemelor de referinta in care se gaseste obiectul si din care se face masuratoarea ;
Presupunerea pleaca de la faptul ca un al doilea sistem de referință S' are axele spatiale si un ceas ce coincide exact cu ale lui S in care se gaseste paralelipipedul la momentul zero,
dar care se misca cu o viteza constanta v în raport cu S' in jurul axei x.
Gama este factorul de transformare Lorentz:
,,gama"=1/sqrt(1-v^2/c^2) este factorul de transformare Lorentz.
Deci masuratoarea in cele 2 SR este legata de dilatarea temporara :
Aceasta arata ca durata de timp dt intre doua batai ale ceasului, pentru sistemul in miscare S este mai mare decat durata de timp dt dintre aceleasi batai masurate in sistemul in care ceasul este in repaus S'
pe Terra de exemplu.
adica dt1=,,gama" dt
In mod corespunzator la contractia lungimii :
dx1= dx/,,gama"
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teoria relativității restrânse - Formule - Întrebări
Re: Teoria relativității restrânse - Formule - Întrebări
Nu risca sa te mai gandesti la asta, ca poti sa ajungiDacu a scris:. . . . .
Dacă volumul relațivist al paralelipipedului tinde la zero atunci asta ar însemna că acest paralelipiped devine inperceptibil pentru ochii observatorului, ceea ce nu este totuna că masa acelui paralelipiped ar tinde la înfinit dar cu siguranță impulsul acestuia ar fi egal cu produsul dintre masa lui în repaus și viteza luminii, atâta tot și nimic altceva.Este aberant să se tragă concluzia că masa acelui paralelipiped ar tinde la infinit dacă viteza acestuia tinde la infinit!
la concluzia incomoda ca totul este aberant in ipoteza
variatiei masei cu viteza.
Timpul compresibil mai ales, este de operă comică !
Pilula asta este sa o înghiti intreaga, nu sa o mesteci !
virgil_48- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 11380




Puncte : 44921
Data de inscriere : 03/12/2013
Pagina 1 din 2 • 1, 2 
 Subiecte similare
Subiecte similare» Nedumeriri privind teoria relativităţii restrânse
» Teoria Relativității - Discuții
» Teoria relativitatii pe intelesul tuturor
» Teoria Relativității - Discuții
» Teoria relativitatii pe intelesul tuturor
Pagina 1 din 2
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 
