Suma de numere prime

Scris de **AMOT** Lun 19 Dec 2011, 08:45

Fie $Suma de numere prime Mimetex$ un numar prim oarecare si $Suma de numere prime Mimetex$ suma tuturor numerelor prime din intervalul $Suma de numere prime Mimetex$ . Sa se demonstreze ca $Suma de numere prime Mimetex$ .

Scris de **curiosul** Lun 19 Dec 2011, 21:35

Foarte interesanta si aceasta observatie!
Felicitari AMOT !!!
Ma ajuta foarte mult ceea ce scrii tu.
O sa analizez in seara asta ce ai scris, dar nu promit ca voi ajunge la un rezultat.
Dar repet, este foarte interesanta observatia.

Scris de **curiosul** Lun 19 Dec 2011, 22:20

Pai AMOT, hai sa o analizam amandoi.
Vezi daca te poate ajuta concluzia la care am ajuns pana acum.
Suma tuturor numerelor impare pana la 2k+1 este egala cu (k+1)^2.
Adica:

$\sum_{k=0}^{n}2k+1=1+3+5+7+...+2n+1=\left ( n+1 \right )^{2}$

Pentru ca orice numar prim mai mare ca 2 este un numar impar, putem rescrie:

$\sum_{k=0}^{P_{n}}2k+1=1+3+5+7+...+2P_{n}+1=\left ( P_{n}+1 \right )^{2}$

Daca notam suma tuturor numerelor prime pana la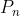 $P_{n}$ cu :

$\sum_{P1}^{P_{n}}p=2+3+5+7+11+...+P_{n}$

ceea ce ai afirmat tu putem sa rescriem ca fiind :

$4\sum_{P_{1}}^{P_{n}}p-\sum_{k=0}^{P_{n}}\left ( 2k+1 \right )\leq 4$

Deci, cu alte cuvinte, daca de 4 ori suma tuturor numerelor prime pana la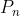 $P_{n}$ , minus suma tuturor numerelor impare pana la $2P_{n}+1$ , este mai mica/egala cu 4, se demonstreaza afirmatia ta.

Scris de **curiosul** Lun 19 Dec 2011, 23:33

Uite demonstratia afirmatiei tale !!!
Plecand de la ce am spus in mesajul anterior, ar trebuie demonstrat doar ca

$4\sum_{P_{1}}^{P_{n}}p\leq \sum_{k=0}^{P_{n}}\left ( 2k+1 \right )$

Dar $4\sum_{k=0}^{\frac{P_{n}-1}{2}}\left ( 2k+1 \right )=\sum_{k=0}^{P_{n}}\left ( 2k+1 \right )$

iar pentru ca

$\sum_{k=0}^{\frac{P_{n}-1}{2}}\left ( 2k+1 \right )=1+3+5+7+9+...P_{n}$

si

$\sum_{P_{1}}^{P_{n}}p=2+3+5+7+11+...P_{n}$

asta inseamna ca

$4\sum_{P_{1}}^{P_{n}}p< 4\sum_{k=0}^{\frac{P_{n}-1}{2}}\left ( 2k+1 \right )= \sum_{k=0}^{P_{n}}\left ( 2k+1 \right )$

Aceasta este demonstratia afirmatiei tale.
Unde nu intelegi intreaba-ma.

Scris de **AMOT** Mar 20 Dec 2011, 08:19

curiosul a scris:Uite demonstratia afirmatiei tale !!!
Plecand de la ce am spus in mesajul anterior, ar trebuie demonstrat doar ca

$4\sum_{P_{1}}^{P_{n}}p\leq \sum_{k=0}^{P_{n}}\left ( 2k+1 \right )$

Dar $4\sum_{k=0}^{\frac{P_{n}-1}{2}}\left ( 2k+1 \right )=\sum_{k=0}^{P_{n}}\left ( 2k+1 \right )$

iar pentru ca

$\sum_{k=0}^{\frac{P_{n}-1}{2}}\left ( 2k+1 \right )=1+3+5+7+9+...P_{n}$

si

$\sum_{P_{1}}^{P_{n}}p=2+3+5+7+11+...P_{n}$

asta inseamna ca

$4\sum_{P_{1}}^{P_{n}}p< 4\sum_{k=0}^{\frac{P_{n}-1}{2}}\left ( 2k+1 \right )= \sum_{k=0}^{P_{n}}\left ( 2k+1 \right )$

Aceasta este demonstratia afirmatiei tale.
Unde nu intelegi intreaba-ma.

Demonstratia ta este gresita........inca de la prima fraza a demonstratie tale caci afirmi ceva gresit!!!!Ultima inegalitate din demonstratia ta este gresita............si ca sa te convingi prticularizeaza ultima inegalitate pentru diversele valori ale lui $Suma de numere prime Mimetex$ .........Demonstratia este simpla dar nu este cea pe care ai dat-o tu.

Scris de **Abel Cavaşi** Mar 20 Dec 2011, 08:57

Problema se poate rezolva în două moduri. Unul dintre ele este cel arătat de curiosul, cu suma numerelor impare, iar altul este prin inducţie matematică.

Era frumos să-l feliciţi pentru încercarea de a-ţi arăta raţionamentul, chiar dacă ar fi greşit puţin undeva. Pe acest forum nu contează atât de mult detaliile, cât contează esenţa. Eu zic să renunţi la tonul ăsta de superioritate căci nu te ajută la nimic.

Scris de **curiosul** Mar 20 Dec 2011, 14:57

Intr-adevar, daca doua demonstratii sunt diferite, asta nu inseamna ca una dintre ele este falsa.
Dar se pare ca am gresit pe undeva si iti explic din nou.
Suma tuturor numerelor impare pana la 2K+1 inclusiv, este egala cu (k+1)^2.
Calculeaza sa te convingi ca nu gresesc.
Daca il consideram pe k ca fiind P(n), atunci suma tuturor numerelor impare pana la 2P(n)+1 este egala cu [P(n)+1]^2.
Calculeaza din nou si vei vedea ca suma tuturor numerelor impare pana la P(n) inclusiv, este de patru ori mai mica decat suma tuturor numerelor impare pana la 2P(n)+1, adica [P(n)+1]^2.
Iar pentru ca suma tuturor numerelor prime pana la P(n) este mai mica decat suma tuturor numerelor impare pana la P(n).
Din ce este scris mai sus, rezulta afirmatia ta.
Dar... ia arata-mi si tu demonstratia ta!!!
Sa vedem cat de simplu ai demonstrat-o.

Scris de **AMOT** Mier 21 Dec 2011, 08:44

Iata demonstratia mea:
$Suma de numere prime Mimetex.cgi?{1+3+5+7+11+13+17+......+p \le 1+3+5+7+9+11+ 13+15+.......$ . Adaugand 1 in ambele parti ale acestei inegalitati rezulta ca $Suma de numere prime Mimetex$ .

Scris de **AMOT** Mier 21 Dec 2011, 08:57

curiosul a scris:Uite demonstratia afirmatiei tale !!!
Plecand de la ce am spus in mesajul anterior, ar trebuie demonstrat doar ca

$4\sum_{P_{1}}^{P_{n}}p\leq \sum_{k=0}^{P_{n}}\left ( 2k+1 \right )$

asta inseamna ca

$4\sum_{P_{1}}^{P_{n}}p< 4\sum_{k=0}^{\frac{P_{n}-1}{2}}\left ( 2k+1 \right )= \sum_{k=0}^{P_{n}}\left ( 2k+1 \right )$

Aceasta este demonstratia afirmatiei tale.
Unde nu intelegi intreaba-ma.

De unde tragi tu concluzia ca este suficient ca sa demonstrezi prima inegalitate cu doar doi termeni din inegalitatea din problema propusa de mine ca astfel sa demonstrezi inegalitatea din problema propusa?????Da te rog valori numerelor prime Pn si ai sa vezi ca cele doua inegalitati scrise de tine sunt gresite.........
Cum demonstrezi tu egalitatea dintre cele doua sume din partea dreapta a celei de-a doua inegalitati scrise de tine?????????

Scris de **AMOT** Mier 21 Dec 2011, 09:29

Abel Cavaşi a scris:Problema se poate rezolva în două moduri. Unul dintre ele este cel arătat de curiosul, cu suma numerelor impare, iar altul este prin inducţie matematică.

Era frumos să-l feliciţi pentru încercarea de a-ţi arăta raţionamentul, chiar dacă ar fi greşit puţin undeva. Pe acest forum nu contează atât de mult detaliile, cât contează esenţa. Eu zic să renunţi la tonul ăsta de superioritate căci nu te ajută la nimic.

Ideea de a demonstra inegalitatea din problema propusa de mine prin metoda inductiei matematice complete am sa incerc sa o aplic dar ceva imi spune ca este mai dificil sau chiar imposibil si asta pentru ca nu se stie care este numarul prim consecutiv numarului prim $Suma de numere prime Mimetex$ caci se stie ca nu se poate gasi o functie de generare a tuturor numerelor prime existente.
Eu nu ma consider superior si atunci cand gresesc imi recunosc greseala iar cand altcineva greseste atunci ii spun fara ocolisuri ca greseste......Mie nu-mi plac dulcegariile si felicitarile si nici gosolaniile si vorbele indecente.Am fost cumva indecent spunand cuiva ca greseste?Nu cred ca am dat dovada de indecenta cand am spus cuiva ca greseste si daca cel care crede ca eu am spus un neadevar spunandu-i ca a gresit atunci eu il rog sa-mi demonstreze ca am gresit spunand acel neadevar despre afirmatiile lui..........

Scris de **Abel Cavaşi** Mier 21 Dec 2011, 14:13

AMOT a scris:Ideea de a demonstra inegalitatea din problema propusa de mine prin metoda inductiei matematice complete am sa incerc sa o aplic dar ceva imi spune ca este mai dificil sau chiar imposibil si asta pentru ca nu se stie care este numarul prim consecutiv numarului prim $Suma de numere prime Mimetex$ caci se stie ca nu se poate gasi o functie de generare a tuturor numerelor prime existente.

Pentru a folosi inducţia nu este necesară cunoaşterea numărului prim consecutiv, ci este suficient să ştim că numărul prim consecutiv este mai mare cu k unităţi, unde k>1 .

Eu nu ma consider superior si atunci cand gresesc imi recunosc greseala iar cand altcineva greseste atunci ii spun fara ocolisuri ca greseste......

Nu este suficient să-ţi recunoşti o greşeală de matematică, ci trebuie să-ţi recunoşti şi o greşeală de comportament. În plus, toţi greşim, dar nu asta trebuie scos în evidenţă. Trebuie scoase în evidenţă lucrurile (pozitive) care ne ajută să ne înfrăţim, nu cele care ne dezbină!

Oricum, te felicit pentru activitatea ta pe acest forum şi cer iertare dacă am fost prea dur!

Scris de **AMOT** Mier 21 Dec 2011, 16:02

Tocmai asta este dificultatea ca nu stim cat de mare este necunoscuta k despre care vorbesti tu in ceea ce priveste numarul prim consecutiv al numarului prim $Suma de numere prime Mimetex$ .......
Eu raman la credinta ca nu am comis o greseala de comportament caci am spus simplu ca demonstratia lui curiosul este gresita si zic ca nu am spus acest fapt pe un ton de superioritate si aroganta sau cu indecenta,dar ma rog daca sunteti toti forumistii de pe acest forum atat de sensibili am sa incerc sa arat greselile unora sau altora in alt mod.........Eu zic ca este bine nu numai sa ne recunoastem toate greselile proprii dar cred ca este bine sa ne aratam unii altora greselile intr-un mod decent ca astfel sa nu mai gresim in acelasi fel..........

Scris de **Abel Cavaşi** Mier 21 Dec 2011, 16:47

AMOT a scris:Tocmai asta este dificultatea ca nu stim cat de mare este necunoscuta k despre care vorbesti tu in ceea ce priveste numarul prim consecutiv al numarului prim $Suma de numere prime Mimetex$ .......

Vezi cum insişti, vezi? De unde provine acel „tocmai” pe care l-ai scos? De ce „tocmai”? Ai înţeles ce am zis mai sus

Pentru a folosi inducţia nu este necesară cunoaşterea numărului prim consecutiv

? Ai citit asta cu atenţie? De ce vii cu „tocmai”? „Tocmai”-ul ăsta nu e o demonstraţie. Aşa vrei tu să demonstrezi că ar fi necesară cunoaşterea numărului prim consecutiv? Dragul meu, este suficient să aplici inducţia pentru un k cel puţin egal cu 2. Deci, inegalitatea este adevărată chiar dacă k=2. Cu cât k este mai mare, cu atât inegalitatea e „şi mai adevărată”. Asta înseamnă inducţie, dealtfel.

Eu raman la credinta ca nu am comis o greseala de comportament caci am spus simplu ca demonstratia lui curiosul este gresita

Păi, curiosul şi-a lăsat pentru o vreme preocupările lui deoparte şi ţi-a arătat cu bunăvoinţă că inegalitatea se demonstrează cu ajutorul numerelor impare şi asta nu ai apreciat deloc, deşi trebuia s-o faci în primul rând. Dimpotrivă, ai sărit la gâtul lui şi te-ai legat de cele mai mici chichiţe, cam cum face Electron pe scientia. Chiar dacă a greşit demonstraţia, n-am văzut nicăieri să recunoşti că, într-adevăr, demonstraţia se bazează pe comparaţia cu suma numerelor impare. E ca şi cum tu ai cerşi pe stradă şi omul ţi-ar da nişte bani ceva mai şifonaţi iar tu ai sări la el că a greşit. Nu asta era mai important? Nu era mai important că el ţi-a arătat un drum minunat de rezolvare?

si zic ca nu am spus acest fapt pe un ton de superioritate si aroganta sau cu indecenta

Asta zici tu, aşa cum zici multe, şi nu-i adevărat. Electron nu vorbeşte pe un ton de superioritate şi de aroganţă?

,dar ma rog daca sunteti toti forumistii de pe acest forum atat de sensibili

Nu toţi (şi aici iar greşeşti generalizând), ci eu. Eu sunt sensibil şi nu pot admite să-i dai în cap celui care te ajută într-un anumit fel.

am sa incerc sa arat greselile unora sau altora in alt mod

Eu îţi recomand să nu vânezi greşelile altora, că de greşeli suntem cu toţii sătui. Vânează lucrurile bune pe care le vezi pe-aici. Alea sunt mai preţioase. Alea să le scoţi în evidenţă din noianul de greşeli pe care le facem cu toţii.

.........Eu zic ca este bine nu numai sa ne recunoastem toate greselile proprii dar cred ca este bine sa ne aratam unii altora greselile intr-un mod decent ca astfel sa nu mai gresim in acelasi fel..........

Tu ascultă-mi sfatul şi vei vedea că progresul nostru va fi mai rapid dacă ne vom descoperi reciproc părţile bune, nu erorile. Erori avem în jurul nostru o infinitate şi ar fi o pierdere de vreme să vorbim numai despre ele. Lucrurile bune sunt mai greu de văzut şi de alea avem nevoie. Eu greşesc necontenit pentru că în Africa mor copii de foame. Cum ar fi să mă gândesc numai la asta?

Scris de **AMOT** Mier 21 Dec 2011, 18:08

Abel Cavasi,
Hai sa incercam sa aplicam metoda inductiei incomplete.....
Fie $Suma de numere prime Mimetex.cgi?{2+3+5+7+11+13+17+.......$ adevarata si atunci sa aratam ca aceasta inegalitate este adevarata si pentru cazul in care la suma suma $Suma de numere prime Mimetex$ adaugam numarul prim $Suma de numere prime Mimetex$ adica urmatorul numar prim care este consecutiv numarului prim $Suma de numere prime Mimetex$ in ambele parti ale inegalitatii obtinand astfel ca $Suma de numere prime Mimetex.cgi?{2+3+5+7+11+13+17+.......$ .
Pe de alta parte putem scrie direct ca $Suma de numere prime Mimetex.cgi?{2+3+5+7+11+13+17+.......$
Acum spune tu ce concluzie putem trage din cele doua inegalitati de mai sus caci acel k induce o mare dificultate de analiza care sa-mi arate ca prin inductia incompleta ar fi adevarata inegalitatea din problema....
Evident ca demonstratia inegalitatii din problema pe care eu am propus-o (deci pe care eu nu am vazut-o nicaieri prin carti sau pe internet) trebuie sa avem in vedere comparatia dintre suma numerelor prime din intervalul $Suma de numere prime Mimetex$ cu suma tuturor numerelor impare din acelasi interval.
Comportamentul meu pe acest forum si de altfel pe toate forumurile consider ca a fost intotdeauna unul decent si fara aroganta dar intodeauna am spus oricui ca a gresit atunci cand a gresit si am spus ca este corect sau bine sau foarte bine sau excelent sau elegant atunci cand consideram ca asa este.
Incercarea lui curiosul de a demonstra inegalitatea propusa de mine consider ca nu este buna si astept sa-mi raspunda la mesajele de mai sus pentru a ma clarifica.......
Daca ne facem ca nu vedem greselile unora sau altora atunci cum putem afla adevarul?
Sunt cazuri cand pun intrebari atunci cand vreau sa inteleg o problema oarecare dar sunt cazuri in care postez probleme sau intrebari desi stiu raspunsul la aceste probleme si intrebari dar nu exclud ca este posibil ca raspunsurile mele sa fie gresite sau mai slabe decat ale altor forumisti de pe orice forum si deci si de pe acest forum.........
In ceea ce priveste Africa sa stii ca mor copii si oameni din cauza foametei pe toate continentele si deci si in Romania.........

Cu stima,

AMOT

Scris de **meteor** Mier 21 Dec 2011, 18:45

pai, da mai domnule Abel Cavasi, ai ceva dreptate, dar daca sa incep si eu sa ma agat de maruntae, o multime de neclaritati apar.
Care este totus politica acestiu forum?! Calitati pozitive si rele deacord ca toti le au (eu insa nu le am, Very Happy

), insa ce intelegem si in ce mod definim pe acel pozitiv si negativ{in contextul dat e important}.Adica eu sa postez online cele mai frumoase (la parerea mea) "descoperiri" ale mele{care nis nu am de gind...}, si pentru ce ????!!!!

Daca imi permiti ma abat putin de la subiect...
Sunt multi, foarte multi(mai nu toata Terra) ce isi pot inainta o ipoteza la solutionarea unei probleme. Insa sint putin si chiar foarte putini pe care ai putea sa le inchizi(fiind ca un specialist bun in domeniu) gura argumentind ca e falsa ipoteza lor, de ce?! da pentru deaceea ca nu au cum. Sint multi ce sunt plini de idei (idei serioase si frumoase), insa din diferite motive (fie financiare, fie de sanatate{i se termina zilele Very Happy

..}, fie ca nu mai vrea persoana cea sa perda timpul aspumra ideii celea. Acestia nu ar dori sa publice (darueasca) oriunde ideea. Plus la toate astea mai sunt (berbedei) academicieni, si cind te duci la el, el intii te intreaba ce studii ai facute, saracul de el, el nu stie ca din 10 probleme ce ias pune sa le rezolve el nici una din ele toata viata nu o va rezolva...
Sa aduc ceva argumente mai la concret: 1) Postulatul lui Bertrand->teorema Cebisev->teorema Serpinschi, citi matematicieni nu s-au folosit de aceste?! 2) Conjenctura celor doi japonezi Simura si Tanimura, care a mai fost apreciata de un neamt, care si acel a presupus ca cel ce va demonstra conjenctura va demonstra Marea Teorema a lui Fermat, ce ia ramas lui A. W?! 3)Multi inventatori contemporani cica sau inspirat aspupra inovatii lor inca de la manuscrisele lui Davinci! un exemplu este I.Sicorski(un constructor de elicoptere); etc.
Ce as propune eu?! Propun ca sa fie infiintata o arhiv-academie, in care orisicine poate veni cu orisice idee minunata, INSA inainte de a fi depusa "ideea"/"ipoteza" academiei, persoana data impreuna cu unul sau citiva specialisti va fi analizata amanuntit, daca se gasesc totusi erori fatale, sau o redescoperire atunci indata ideea/ipoteza va fi respinsa. In caz contrar cel ce depune cererea va obtine un "drept" de autor, si acel ce poate cindva o va demonstra aceasta idee/ipoteza , teorema/ideea va fi numita in numele: 1)cel ce o demonstreaza- 2)cel ce cindva a depus ideea data la arhiv academie.
Pentru ce mai trebu bataia asta de cap si harababura asta?! Ei, pare la inceput ca e un fleac insa nu e chiar asa.
Cind a incepun sa se evidentieze criza energetica (caatare ea nici nu este, este o politica camumflata), cercetasii sau trezit ca puisorii de dimineata... Insa sint si pot aparea probleme destul destul de grave, solutionarea lor va necesita un timp extrem de scurt (spre exemplu aparitia unei epidemii din o anumita clasa de boli), si daca stiinta e slab dezvoltata in domeniul dat (si nici inchipuire nu are despre solutionare), atunci am rupt cuiu... citeodata o idee buna (spusa cindva) e un lucru sfint.

Scris de **Abel Cavaşi** Joi 22 Dec 2011, 09:02

AMOT a scris:Acum spune tu ce concluzie putem trage din cele doua inegalitati de mai sus caci acel k induce o mare dificultate de analiza care sa-mi arate ca prin inductia incompleta ar fi adevarata inegalitatea din problema....

Mai trebuie să compari termenul din dreapta al primei inegalităţi cu termenul din dreapta al celei de-a doua inegalităţi. Dacă primul este mai mic sau egal decât al doilea pentru orice k natural, atunci ai terminat inducţia.

Pentru restul chestiunilor deschideţi alte topice în locuri potrivite ca să vă răspund la întrebările puse.

Scris de **AMOT** Sam 24 Dec 2011, 07:17

Abel Cavaşi a scris:
AMOT a scris:Acum spune tu ce concluzie putem trage din cele doua inegalitati de mai sus caci acel k induce o mare dificultate de analiza care sa-mi arate ca prin inductia incompleta ar fi adevarata inegalitatea din problema....
Mai trebuie să compari termenul din dreapta al primei inegalităţi cu termenul din dreapta al celei de-a doua inegalităţi. Dacă primul este mai mic sau egal decât al doilea pentru orice k natural, atunci ai terminat inducţia.

Pentru restul chestiunilor deschideţi alte topice în locuri potrivite ca să vă răspund la întrebările puse.

Nu inteleg!Comparatia asta am facut-o dar nu reiese clar ca se poate demonstra inegalitatea propusa de mine prin metoda inductiei complete.Orice tip de inegalitate se poate demonstra prin inductie matematica completa?

Scris de **Abel Cavaşi** Sam 24 Dec 2011, 09:18

AMOT a scris:Nu inteleg!

Ok, ne străduim să te facem să înţelegi, atunci.

Comparatia asta am facut-o dar nu reiese clar ca se poate demonstra inegalitatea propusa de mine prin metoda inductiei complete.

Nu reiese clar? Hmmm... Ai putea să ne demonstrezi că „nu reiese clar”? Chiar sunt curios să văd dacă am omis eu ceva.

Orice tip de inegalitate se poate demonstra prin inductie matematica completa?

Nu. De exemplu, unele inegalităţi cu numere reale nu merită demonstrate cu inducţie. Inducţia se aplică mai ales la numere întregi.

Scris de Continut sponsorizat

Suma de numere prime

Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime

Re: Suma de numere prime