Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Meteorr Ieri la 21:34
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Joi 21 Noi 2024, 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la virgil în Carti sau documente de care avem nevoie
( 1 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 1 )
» Mesaj de la eugen în Ce fel de popor suntem
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Dacu2 | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Abel Cavaşi |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| virgil | ||||
| Dacu2 | ||||
| CAdi | ||||
| Meteorr | ||||
| ilasus | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 28 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 28 Vizitatori :: 3 Motoare de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Inca o ecuatie cu factoriale
2 participanți
Pagina 1 din 1
 Inca o ecuatie cu factoriale
Inca o ecuatie cu factoriale
Sa se rezolve ecuatia  stiind ca
stiind ca  sunt numere naturale diferite intre ele.
sunt numere naturale diferite intre ele.
_________________
"La inceput era CUVANTUL si CUVANTUL era la DUMNEZEU si DUMNEZEU era CUVANTUL."
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
Nu vrea nimeni sa rezolve ecuatia??????Nu va plac factorialele???????? 
_________________
"La inceput era CUVANTUL si CUVANTUL era la DUMNEZEU si DUMNEZEU era CUVANTUL."
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
Faceti greva si la factorialele astea?????
_________________
"La inceput era CUVANTUL si CUVANTUL era la DUMNEZEU si DUMNEZEU era CUVANTUL."
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
Se pare ca ecuatia  nu are solutii pentru x,y,z naturale diferite .
nu are solutii pentru x,y,z naturale diferite .
Daca sunt diferite, atunci Y, sa spunem, este mai mare decat x, iar produsul celor doua factoriale il scriem ca:
\cdot \left ( x+2 \right )\cdot ...\cdot y)
Din relatia de mai sus, se observa ca pentru x=1, produsul celor doua factoriale poate fi un alt factorial dar asta inseamna ca y=z si nu corespunde conditiilor pe care le-ai pus, adica x,y,z naturale diferite.
Daca x este mai mare ca 1, atunci prima serie de produse, adica a acelor patrate perfecte, nu sunt numere naturale consecutive pana la x+1, deci nu poate fi un factorial.
Daca sunt diferite, atunci Y, sa spunem, este mai mare decat x, iar produsul celor doua factoriale il scriem ca:
Din relatia de mai sus, se observa ca pentru x=1, produsul celor doua factoriale poate fi un alt factorial dar asta inseamna ca y=z si nu corespunde conditiilor pe care le-ai pus, adica x,y,z naturale diferite.
Daca x este mai mare ca 1, atunci prima serie de produse, adica a acelor patrate perfecte, nu sunt numere naturale consecutive pana la x+1, deci nu poate fi un factorial.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
curiosul,
Rationamentul tau este gresit...... Sunt solutii x,y,z naturale diferite intre ele!Astept si alte raspunsuri de la tine si de la altii.......
Sunt solutii x,y,z naturale diferite intre ele!Astept si alte raspunsuri de la tine si de la altii....... 
Rationamentul tau este gresit......
_________________
"La inceput era CUVANTUL si CUVANTUL era la DUMNEZEU si DUMNEZEU era CUVANTUL."
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
Iata o solutie:
 .
.
Mai sunt si alte solutii.....
Mai sunt si alte solutii.....
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
Cercetati (cautati) toate solutiile?????? 
_________________
"La inceput era CUVANTUL si CUVANTUL era la DUMNEZEU si DUMNEZEU era CUVANTUL."
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
Ai dreptate. Sunt o infinitate de solutii.
Si sunt date de formula!=\left ( n! \right )!)
Ecuatia nu are solutii pentru z numar prim, pentru ca acesta nu poate fi exprimat ca produs de mai mult de doua numere naturale consecutive, singurul caz fiind z=2, care nu este o solutie a ecuatiei.
Ecuatia nu cred ca poate avea alte solutii decat cele care rezulta prin formula de mai sus, dar n-am analizat-o mai detaliat.
Nici nu sunt o prioritate pentru mine ecuatiile astea.
Si daca nu ti-a mai raspuns si altcineva pana acum, inseamna ca nici pentru altcineva nu sunt o prioritate.
Si sunt date de formula
Ecuatia nu are solutii pentru z numar prim, pentru ca acesta nu poate fi exprimat ca produs de mai mult de doua numere naturale consecutive, singurul caz fiind z=2, care nu este o solutie a ecuatiei.
Ecuatia nu cred ca poate avea alte solutii decat cele care rezulta prin formula de mai sus, dar n-am analizat-o mai detaliat.
Nici nu sunt o prioritate pentru mine ecuatiile astea.
Si daca nu ti-a mai raspuns si altcineva pana acum, inseamna ca nici pentru altcineva nu sunt o prioritate.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
curiosul,
Asa zisele solutii date de tine sunt evidente caci rezulta din insasi identitatea! \cdot x}) pentru
pentru  si care nu sunt interesante deoarece te folsesti de trucul identitatii banale......
si care nu sunt interesante deoarece te folsesti de trucul identitatii banale......  Cu ce formula obtii solutia
Cu ce formula obtii solutia  ???
??? 
Din ecuatia propusa de mine rezulta imediat ca exista o relatie de ordine intre .....Care este aceasta relatie de ordine si cum putem incerca,avand in vedere aceasta relatie de ordine,sa rezolvam deci ecuatia
.....Care este aceasta relatie de ordine si cum putem incerca,avand in vedere aceasta relatie de ordine,sa rezolvam deci ecuatia  ???
??? 
Asa zisele solutii date de tine sunt evidente caci rezulta din insasi identitatea
Din ecuatia propusa de mine rezulta imediat ca exista o relatie de ordine intre
_________________
"La inceput era CUVANTUL si CUVANTUL era la DUMNEZEU si DUMNEZEU era CUVANTUL."
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
Da Amot.
Ai dreptate.
Si se pare ca ecuatia este un pic mai interesanta decat pare la prima vedere, pentru ca in cautarea solutiilor, intervine ceea ce imi place:
factorizarea.
Pentru ca 1x2x3x4x5x6=1x(2x4)x(2x5)x(3x3)=1x8x9x10 si este exact continuarea factorialului 7.
O sa o analizez deseara mai detaliat, sa vad daca gasesc o relatie care ordoneaza solutiile ecuatiei.
Intr-adevar e interesanta.
Pentru in factorizare apar numerele prime si o astfel de relatie poate fi exprimata in functie de numerele prime.
Iti raspund diseara ca acum tre sa plec la servici.
Cu stima.
Ai dreptate.
Si se pare ca ecuatia este un pic mai interesanta decat pare la prima vedere, pentru ca in cautarea solutiilor, intervine ceea ce imi place:
factorizarea.
Pentru ca 1x2x3x4x5x6=1x(2x4)x(2x5)x(3x3)=1x8x9x10 si este exact continuarea factorialului 7.
O sa o analizez deseara mai detaliat, sa vad daca gasesc o relatie care ordoneaza solutiile ecuatiei.
Intr-adevar e interesanta.
Pentru in factorizare apar numerele prime si o astfel de relatie poate fi exprimata in functie de numerele prime.
Iti raspund diseara ca acum tre sa plec la servici.
Cu stima.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
curiosul,
Incepi sa te apropii de rezolvare...... Cum putem gasi toate solutiile ecuatiei?????Exista vreo formula???
Cum putem gasi toate solutiile ecuatiei?????Exista vreo formula??? 
Incepi sa te apropii de rezolvare......
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
Necunoscuta z din acea ecuatie poate fi numar impar????????curiosul a scris:Ecuatia nu are solutii pentru z numar prim, pentru ca acesta nu poate fi exprimat ca produs de mai mult de doua numere naturale consecutive, singurul caz fiind z=2, care nu este o solutie a ecuatiei.
_________________
"La inceput era CUVANTUL si CUVANTUL era la DUMNEZEU si DUMNEZEU era CUVANTUL."
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
Ti-am analizat ecuatia.
Este intr-adevar interesanta.
Dar nu cred ca mai sunt alte solutii in afara celor care rezulta din formula clasica, pe care ti-am aratat-o,
n! x (n!-1)!=(n!)!
si exceptia pe care ai spus-o tu 6! x 7!= 10!.
O demonstratie pentru asta este ceva mai costisitoare pentru ca rationamentul demonstratiei este strans legat de distributia numerelor prime.
Oricum, eu am inceput sa plec de la rationamentul:
Daca notam t! cu
\cdot \left ( a+2 \right )\cdot ...\cdot \left ( a+k \right )=t!) ,
,
atunci
!=\left ( a+k \right )!)
Daca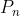 este cel mai mare numar prim care divide produsul
este cel mai mare numar prim care divide produsul  ,
,
acesta din urma nu este in niciun caz un factorial daca nu se divide cel putin cu}) ,
,
unde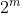 este mai mic decat
este mai mic decat 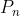 ,
,
adica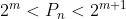 .
.
Pentru ca de la 1 la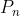 , din 2 in 2 sunt numere care se divid cu 2, din 4 in 4 sunt numere care se divid si cu 4, din 8 in 8 numere care se divid si cu 8 etc, iar pentru ca factorialul este un produs trebuie sa se divida cel putin cu
, din 2 in 2 sunt numere care se divid cu 2, din 4 in 4 sunt numere care se divid si cu 4, din 8 in 8 numere care se divid si cu 8 etc, iar pentru ca factorialul este un produs trebuie sa se divida cel putin cu }) .
.
Dar nu numai.
La fel trebuie procedat si cu toate numerele prime mai mici decat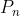 cel putin.
cel putin.
Cu alte cuvinte, produsul trebuie sa se divida cu cel putin toate numerele prime mai mici decat
trebuie sa se divida cu cel putin toate numerele prime mai mici decat 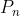 .
.
Este prima conditie insuficienta dar NECESARA ca produsul sa poata fi un factorial.
sa poata fi un factorial.
Implica cumva indirect ca niciunul din termenii produsului\cdot \left ( a+2 \right )\cdot ...\cdot \left ( a+k \right )) sa nu fie prim, ca acest produs sa poata fi un factorial.
sa nu fie prim, ca acest produs sa poata fi un factorial.
Pentru moment nu reusesc sa demonstrez dar din cate am calculat sansele sunt mici sa mai fie o astfel de solutie care sa fie exceptia de la formula clasica.
O sa mai incerc totusi.
Poate ma insel.
Este intr-adevar interesanta.
Dar nu cred ca mai sunt alte solutii in afara celor care rezulta din formula clasica, pe care ti-am aratat-o,
n! x (n!-1)!=(n!)!
si exceptia pe care ai spus-o tu 6! x 7!= 10!.
O demonstratie pentru asta este ceva mai costisitoare pentru ca rationamentul demonstratiei este strans legat de distributia numerelor prime.
Oricum, eu am inceput sa plec de la rationamentul:
Daca notam t! cu
atunci
Daca
acesta din urma nu este in niciun caz un factorial daca nu se divide cel putin cu
unde
adica
Pentru ca de la 1 la
Dar nu numai.
La fel trebuie procedat si cu toate numerele prime mai mici decat
Cu alte cuvinte, produsul
Este prima conditie insuficienta dar NECESARA ca produsul
Implica cumva indirect ca niciunul din termenii produsului
Pentru moment nu reusesc sa demonstrez dar din cate am calculat sansele sunt mici sa mai fie o astfel de solutie care sa fie exceptia de la formula clasica.
O sa mai incerc totusi.
Poate ma insel.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
curiosul,
Obsesia ta pentru numerele prime te departeaza de gasirea solutilor ecuatiei......
Demonstratia ca z nu e numar prim in cazul ecuatiei propuse in acele conditii este simpla si evidenta daca tu incerci sa rezolvi ecuatia considerand o relatie ordine intre numerele x,y,z pentru ca acestea sa fie diferite intre ele....
Numarul z din ecuatia propusa de mine in acele conditii poate fi numar impar????????
Obsesia ta pentru numerele prime te departeaza de gasirea solutilor ecuatiei......
Demonstratia ca z nu e numar prim in cazul ecuatiei propuse in acele conditii este simpla si evidenta daca tu incerci sa rezolvi ecuatia considerand o relatie ordine intre numerele x,y,z pentru ca acestea sa fie diferite intre ele....
Numarul z din ecuatia propusa de mine in acele conditii poate fi numar impar????????
_________________
"La inceput era CUVANTUL si CUVANTUL era la DUMNEZEU si DUMNEZEU era CUVANTUL."
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
Obsesia mea pentru numere prime, nu ma departeaza de gasirea solutiilor ci ma ajuta sa inteleg ca nu mai pot fi altele.
Ai mai gasit tu vreuna?
Ai mai gasit tu vreuna?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
Pentru ca daca P(n) este cel mai mare numar prim care divide produsul :
a(a+1)(a+2)(a+3)...(a+k), conditia numarul 1 ca acest produs sa fie un factorial 1*2*3*4*..*t, este ca produsul
a(a+1)(a+2)(a+3)...(a+k) sa se divida cu cel putin orice numar prim mai mic/egal cu P(n).
Daa exista vreun numar prim mai mic decat P(n) care nu divide a(a+1)(a+2)(a+3)...(a+k), atunci factorialul t! nu contine nici acel numar prim nici vreun multiplu al sau, si pentru ca factorialul nu poate fi mai mic decat acel numar prim P(n) adica cel mai mare numar prim care divide a(a+1)(a+2)(a+3)...(a+k), produsul a(a+1)(a+2)(a+3)...(a+k), nu poate fi un factorial.
Daca a(a+1)(a+2)(a+3)...(a+k) nu este un factorial t!, atunci nu are loc relatia
t! * (a-1)!=(a+k)!
De aceea cred eu ca nu mai pot fi alte solutii, nu din cauza obsesiilor.
Singurele solutii sunt exceptia pe care ai aratat-o:
6!*7!=10! si cele care rezulta din formula:
n!*(n!-1)!=(n!)!
Ai mai gasit tu vreuna?
a(a+1)(a+2)(a+3)...(a+k), conditia numarul 1 ca acest produs sa fie un factorial 1*2*3*4*..*t, este ca produsul
a(a+1)(a+2)(a+3)...(a+k) sa se divida cu cel putin orice numar prim mai mic/egal cu P(n).
Daa exista vreun numar prim mai mic decat P(n) care nu divide a(a+1)(a+2)(a+3)...(a+k), atunci factorialul t! nu contine nici acel numar prim nici vreun multiplu al sau, si pentru ca factorialul nu poate fi mai mic decat acel numar prim P(n) adica cel mai mare numar prim care divide a(a+1)(a+2)(a+3)...(a+k), produsul a(a+1)(a+2)(a+3)...(a+k), nu poate fi un factorial.
Daca a(a+1)(a+2)(a+3)...(a+k) nu este un factorial t!, atunci nu are loc relatia
t! * (a-1)!=(a+k)!
De aceea cred eu ca nu mai pot fi alte solutii, nu din cauza obsesiilor.
Singurele solutii sunt exceptia pe care ai aratat-o:
6!*7!=10! si cele care rezulta din formula:
n!*(n!-1)!=(n!)!
Ai mai gasit tu vreuna?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
curiosul,
Eu am propus o problema si te rog foloseste datele problemei adica x,y si z ca e greu sa inteleg ce spui.....ai obsesia numerelor prime si mai bagi si alte necunoscute cum ar fi Pn si a.......Cine este a si de unde rezulta prin rationamentul tau???????
Eu am propus o problema si te rog foloseste datele problemei adica x,y si z ca e greu sa inteleg ce spui.....ai obsesia numerelor prime si mai bagi si alte necunoscute cum ar fi Pn si a.......Cine este a si de unde rezulta prin rationamentul tau???????
_________________
"La inceput era CUVANTUL si CUVANTUL era la DUMNEZEU si DUMNEZEU era CUVANTUL."
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
Sa vad cat timp am acum.
Daca nu o sa-ti dezvolt mai logic toata explicatia diseara pentru ca acum nu am timp sa folosesc LaTex-ul.
Oricum,
deci putem gasi solutii, acestea fiind infinite, prin formula generala a factorialului, inlocuind necunoscuta cu un factorial:
n! * (n!-1)! = (n!)!
Tu ai gasit o exceptie de la regula prin exemplul :
6! * 7! = 10!
Din cate am analizat, nu mai pot exista alte solutii, sau sansele sunt extrem de mici ca sa mai poata fi o alta solutie ca si exceptie de la prima formula.
Poti sa imparti un factorial in doua produse, unul care contine numerele naturale consecutive pana la m, sa spunem si unul care sa contina toate numerele naturale consecutive de la m+1 la t.
Ecuatia ta are solutii daca putem exprima produsul de la m+1 la t ca un factorial de x, adica un produs de la 1 la x.
Dar daca produsul de la m+1 la t se divide cu cel mai mare numar prim p(n), ca sa poata fi un factorial, produsul de la m+1 la t, trebuie sa se divida cu toate numerele prime mai mici decat P(n).
Pentru ca daca produsul de la m+1 la t se divide cu P(n), nu poti exprima acest produs sub forma de alt produs care sa nu contina ca si factor , acest numar prim P(n).
Deci asta inseamna ca si factorialul sub forma in care ar putea fi scris produsul de la m+1 la t, trebuie sa contina pe P(n).
Dar si orice numar prim mai mic decat P(n), pentru ca factorialul trebuie sa contina TOATE numerele prime pana la P(n).
Alegand aleatoriu un interval de numere consecutive, asta inseamna ca in factorizarea acelor numere sa apara orice numar prim pana la un cel mai mare numar prim care divide unul dintre acei factori.
Probabilitatea este mica.
Foarte mica.
O sa-ti explic mai detaliat diseara, cu un rationament mai simp[lu.
Daca nu o sa-ti dezvolt mai logic toata explicatia diseara pentru ca acum nu am timp sa folosesc LaTex-ul.
Oricum,
deci putem gasi solutii, acestea fiind infinite, prin formula generala a factorialului, inlocuind necunoscuta cu un factorial:
n! * (n!-1)! = (n!)!
Tu ai gasit o exceptie de la regula prin exemplul :
6! * 7! = 10!
Din cate am analizat, nu mai pot exista alte solutii, sau sansele sunt extrem de mici ca sa mai poata fi o alta solutie ca si exceptie de la prima formula.
Poti sa imparti un factorial in doua produse, unul care contine numerele naturale consecutive pana la m, sa spunem si unul care sa contina toate numerele naturale consecutive de la m+1 la t.
Ecuatia ta are solutii daca putem exprima produsul de la m+1 la t ca un factorial de x, adica un produs de la 1 la x.
Dar daca produsul de la m+1 la t se divide cu cel mai mare numar prim p(n), ca sa poata fi un factorial, produsul de la m+1 la t, trebuie sa se divida cu toate numerele prime mai mici decat P(n).
Pentru ca daca produsul de la m+1 la t se divide cu P(n), nu poti exprima acest produs sub forma de alt produs care sa nu contina ca si factor , acest numar prim P(n).
Deci asta inseamna ca si factorialul sub forma in care ar putea fi scris produsul de la m+1 la t, trebuie sa contina pe P(n).
Dar si orice numar prim mai mic decat P(n), pentru ca factorialul trebuie sa contina TOATE numerele prime pana la P(n).
Alegand aleatoriu un interval de numere consecutive, asta inseamna ca in factorizarea acelor numere sa apara orice numar prim pana la un cel mai mare numar prim care divide unul dintre acei factori.
Probabilitatea este mica.
Foarte mica.
O sa-ti explic mai detaliat diseara, cu un rationament mai simp[lu.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
curiosul,
Ma exasperezi cu numerele tale prime!!!!Conform ecuatiei propuse rezulta ori ori
ori  .Sa presupunem
.Sa presupunem  atunci evident rezulta ca
atunci evident rezulta ca (x+2).....(y-1)y}) si
si (x+2)...y(y+1)(y+2)....(z-1)z}) si deci ecuatia devine
si deci ecuatia devine (x+2)........(y-1)y=(x+1)(x+2).......y(y+1)(y+2).....(z-1)z}) adica
adica (y+2)......(z-1)z}) .Putem scrie ca
.Putem scrie ca  unde
unde  .Cum rezolvam in continuare?????Recunosc ca inca mai cercetez sa gasesc si alte solutii diferite de cele evidente rezultate din identitatea banala
.Cum rezolvam in continuare?????Recunosc ca inca mai cercetez sa gasesc si alte solutii diferite de cele evidente rezultate din identitatea banala !=(z!-1)!z!}) si solutia x=6,y=7,z=10.
si solutia x=6,y=7,z=10. 
Ma exasperezi cu numerele tale prime!!!!Conform ecuatiei propuse rezulta ori
_________________
"La inceput era CUVANTUL si CUVANTUL era la DUMNEZEU si DUMNEZEU era CUVANTUL."
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
Salut AMOT !
In primul rand te exasperezi degeaba.
Ai dezvoltat corect factorialii, insa aceasta dezvoltare nu te ajuta sa gasesti solutii.
Rationamentul meu care te exaspereaza, arata ca probabilitatea sa mai existe alte solutii este foarte, foarte mica.
De ce ?
Pentru ca:
\left ( n-1 \right )n)
Pana aici suntem de acord.
Daca necunoscuta n de mai sus este z-ul din ecuatia ta,atunci z il putem exprima ca fiind produsul dintre numerele consecutive pana la x,
unde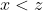 si ceilalti factori care raman pana la z, adica:
si ceilalti factori care raman pana la z, adica:
\left ( x+2 \right )\cdot ...\cdot \left ( z-2 \right )\left ( z-1 \right )z)
\left ( x+2 \right )\cdot ...\cdot \left ( z-2 \right )\left ( z-1 \right )z)
Singura problema care se ridica acum este, exista x, z astfel incat:
\left ( x+2 \right )\cdot ...\cdot \left ( z-2 \right )\left ( z-1 \right )z) ???
???
Nu stim, dar incercam sa intelegem daca exista o conditie minima ca acel produs,
\left ( x+2 \right )\cdot ...\cdot \left ( z-2 \right )\left ( z-1 \right )z)
sa poata fi un factorial, adica:
\left ( x+2 \right )\cdot ...\cdot \left ( z-2 \right )\left ( z-1 \right )z)
Si se pare ca exista o asemenea conditie.
Fie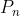 , cel mai mare numar prim care divide produsul
, cel mai mare numar prim care divide produsul \cdot \left ( x+2 \right )\cdot ...\cdot \left ( z-2 \right )\cdot \left ( z-1 \right )z) .
.
Asta inseamna ca, fie unul din factorii produsului este numarul prim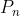 , fie unul din factori se divide cu
, fie unul din factori se divide cu 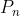 .
.
Mai babeste, fie factorii produsului:

In acest caz, 23 este cel mai mare numar prim care divide produsul respectiv.
Dar pentru ca pe 23 nu il poti exprima ca un produs de numere prime mai mici decat acesta, inseamna ca nu poti exprima produsul fara ca unul din factori sa fie 23,
iar asta inseamna si ca incercand sa scrii produsul ca fiind un factorial, adica ca un produs de la 1 la y, implica direct ca 23 trebuie sa fie mai mic cel putin egal cu y,
ca fiind un factorial, adica ca un produs de la 1 la y, implica direct ca 23 trebuie sa fie mai mic cel putin egal cu y,
pentru ca daca desfaci in factori primi produsul , obtii :
, obtii :
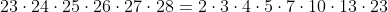
Dar acesta nu este un factorial ; nu contine toate numerele consecutive pana la 23.
Din ce am scris mai sus, rezulta, dupa cum te-am exasperat si pana acum, ca produsul\cdot \left ( x+2 \right )\cdot ...\cdot \left ( z-1 \right )z) TREBUIE sa se divida cu cel putin toate numerele prime mai mici decat
TREBUIE sa se divida cu cel putin toate numerele prime mai mici decat 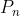 ,
,
unde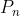 este cel mai mare numar prim care divide produsul
este cel mai mare numar prim care divide produsul
\cdot \left ( x+2 \right )\cdot ...\cdot \left ( z-1 \right )z) .
.
Este prima conditie.
Daca nu este indeplinita nu poti exprima acel produs ca fiid un factorial.
Din exemplul tau,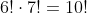 , rezulta ca
, rezulta ca
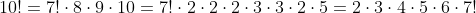
deci ca:
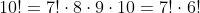 .
.
Din ceea ce ti-am scris, pentru mine probabilitatea sa mai fie inca o solutie, exceptie de la formula clasica, din cate inteleg distributia numerelor prime, NU MAI EXISTA.
Pentru mine nu mai este important sa incerc sa-ti si demonstrez asta.
Tu poti sa cauti in continuare daca tii neaparat sa gasesti solutii, asa ca :
Exasperare placuta in continuare si Paste fericit!
In primul rand te exasperezi degeaba.
Ai dezvoltat corect factorialii, insa aceasta dezvoltare nu te ajuta sa gasesti solutii.
Rationamentul meu care te exaspereaza, arata ca probabilitatea sa mai existe alte solutii este foarte, foarte mica.
De ce ?
Pentru ca:
Pana aici suntem de acord.
Daca necunoscuta n de mai sus este z-ul din ecuatia ta,atunci z il putem exprima ca fiind produsul dintre numerele consecutive pana la x,
unde
Singura problema care se ridica acum este, exista x, z astfel incat:
Nu stim, dar incercam sa intelegem daca exista o conditie minima ca acel produs,
sa poata fi un factorial, adica:
Si se pare ca exista o asemenea conditie.
Fie
Asta inseamna ca, fie unul din factorii produsului este numarul prim
Mai babeste, fie factorii produsului:
In acest caz, 23 este cel mai mare numar prim care divide produsul respectiv.
Dar pentru ca pe 23 nu il poti exprima ca un produs de numere prime mai mici decat acesta, inseamna ca nu poti exprima produsul fara ca unul din factori sa fie 23,
iar asta inseamna si ca incercand sa scrii produsul
pentru ca daca desfaci in factori primi produsul
Dar acesta nu este un factorial ; nu contine toate numerele consecutive pana la 23.
Din ce am scris mai sus, rezulta, dupa cum te-am exasperat si pana acum, ca produsul
unde
Este prima conditie.
Daca nu este indeplinita nu poti exprima acel produs ca fiid un factorial.
Din exemplul tau,
deci ca:
Din ceea ce ti-am scris, pentru mine probabilitatea sa mai fie inca o solutie, exceptie de la formula clasica, din cate inteleg distributia numerelor prime, NU MAI EXISTA.
Pentru mine nu mai este important sa incerc sa-ti si demonstrez asta.
Tu poti sa cauti in continuare daca tii neaparat sa gasesti solutii, asa ca :
Exasperare placuta in continuare si Paste fericit!
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Inca o ecuatie cu factoriale
Re: Inca o ecuatie cu factoriale
Salut curiosul!
Din(y+2)......(z-1)z}) si
si  unde
unde  rezulta ca
rezulta ca !-x!=k \cdot y}) unde
unde  este un numar intreg.....
este un numar intreg..... 
Iti doresc sa pasti in liniste si pace pe campul tau de numere prime pana la batranete.......
Din
Iti doresc sa pasti in liniste si pace pe campul tau de numere prime pana la batranete.......
_________________
"La inceput era CUVANTUL si CUVANTUL era la DUMNEZEU si DUMNEZEU era CUVANTUL."
AMOT- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 1122




Puncte : 18498
Data de inscriere : 07/12/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 