Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Forever_Man Astazi la 18:21
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 1 )
» Mesaj de la Abel Cavaşi în Daci nemuritori
( 1 )
» Mesaj de la CAdi în Fenomene Electromagnetice
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12458) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Dacu2 | ||||
| Forever_Man | ||||
| Abel Cavaşi | ||||
| Meteorr |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| Dacu2 | ||||
| virgil | ||||
| CAdi | ||||
| eugen | ||||
| Meteorr | ||||
| ilasus | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 51 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 51 Vizitatori Nici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Despre forumul personal al lui meteor
5 participanți
Pagina 1 din 2
Pagina 1 din 2 • 1, 2 
 Despre forumul personal al lui meteor
Despre forumul personal al lui meteor
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 19:28, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
Cred că omul doar voia să-și expună rezultatele mai sistematizat și așezat. Cred că e greu să faci asta dacă e un subiect de care mulți oameni sunt interesați. Mai bine să fie expunerea într-un loc și discuțiile în alta. Dacă a greșit și ai timp și pricepere să-i arăți asta, dă-i fără milă  , eu am fost cel mult spectator la probleme de teoria numerelor, nu mi-aș permite să mă apuc să-i spun unde-i bine unde nu-i bine.
, eu am fost cel mult spectator la probleme de teoria numerelor, nu mi-aș permite să mă apuc să-i spun unde-i bine unde nu-i bine.

omuldinluna- Ne-a părăsit
- Mulţumit de forum : Prenume : Omul




Numarul mesajelor : 2728
Puncte : 30680
Data de inscriere : 03/08/2011
Obiective curente : Doresc sa termin expunerea problemei clasice a miscarii in camp central, cu aplicatie la campul gravitational Newtonian
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
https://cercetare.forumgratuit.ro/t916-de-ce-forumul-personal#26529
Acesta "interzicere" sau filtru prea din prea, desigur poate face ca pe unii sa se supere.
Am interzis deoarece sa nu survina WoodyCad, Sandocan, etc. (personal si cu ei nimic concret nu am, insa absolut deloc nu is deacord cu modul in care ei comunica).
Eu vreau sa fie totul ce e mai finisat si interesant la un loc, frumos aranjat.
Nu ca de la al doilea mesaj sa vina WoodyCad si sa imi inceapa a spune de rime si fel de fel, apoi urmeaza sa ii raspund, apoi mai urmeaza niste glume, si gata. Se face o varza totala, cine a trece si avrea sa vada ceva coincis si frumos, ii va fi lehamite.
Am spus, ca cine vrea sa spuna ceva la subiect, sa spuna sau prin privat sau public deoparte.
Bine facem asa, ca Abel sa permita accesul tuturor, intradevar poate unii au ceva important de reprosat insa se sfiesc.
Dupa cum stii bine @curiosu, 95% din comentariile mele sunt mai mult intrebari si ipoteze.
Functia ceea (anticvariatul) am aplicat-o ca sa fie cit posibil mai simplistic.
Eu am spus, ca am putut lua, spre exemplu, functiile lui P.D., acelea fiind muult mai puternice.
Daca eu cu aceasta am rezolvat, cu acele cu atit mai mult, doar ca acolo domeniul de definitie putin mai de departe incepe (pe la 350000), asta nu e mare problema.
Ca sa demonstrez ca anticvariatul nu e gresit in al aplica, se poate asa:
Demonstrez ca pe cel putin [350;+inf) [cu toate ca perge si pe [3;+inf) ] nu exista nici o solutie la intersectia acestor grafice.
Apoi e deajuns de luat doar o proba,proba sa fie de pe domeniul de definitie, ca sa aflam care functie e mai mare pentru acesta valoare.
Aflind proba, demonstram ca pe intreg intervalul definit cutarea functie este > ca cealalta functie.
Am luat anticvariatul deoarece este foarte simplu, compact.
Ce sa mai scriu formularai, daca foarte bine a mers cu aceasta functie. Demonstratiile au mers. Daca insa, nu mergeau, atunci intradevar trebuia sa apelez la alte functii.
Acesta "interzicere" sau filtru prea din prea, desigur poate face ca pe unii sa se supere.
Am interzis deoarece sa nu survina WoodyCad, Sandocan, etc. (personal si cu ei nimic concret nu am, insa absolut deloc nu is deacord cu modul in care ei comunica).
Eu vreau sa fie totul ce e mai finisat si interesant la un loc, frumos aranjat.
Nu ca de la al doilea mesaj sa vina WoodyCad si sa imi inceapa a spune de rime si fel de fel, apoi urmeaza sa ii raspund, apoi mai urmeaza niste glume, si gata. Se face o varza totala, cine a trece si avrea sa vada ceva coincis si frumos, ii va fi lehamite.
Am spus, ca cine vrea sa spuna ceva la subiect, sa spuna sau prin privat sau public deoparte.
Bine facem asa, ca Abel sa permita accesul tuturor, intradevar poate unii au ceva important de reprosat insa se sfiesc.
Dupa cum stii bine @curiosu, 95% din comentariile mele sunt mai mult intrebari si ipoteze.
Functia ceea (anticvariatul) am aplicat-o ca sa fie cit posibil mai simplistic.
Eu am spus, ca am putut lua, spre exemplu, functiile lui P.D., acelea fiind muult mai puternice.
Daca eu cu aceasta am rezolvat, cu acele cu atit mai mult, doar ca acolo domeniul de definitie putin mai de departe incepe (pe la 350000), asta nu e mare problema.
Ca sa demonstrez ca anticvariatul nu e gresit in al aplica, se poate asa:
Demonstrez ca pe cel putin [350;+inf) [cu toate ca perge si pe [3;+inf) ] nu exista nici o solutie la intersectia acestor grafice.
Apoi e deajuns de luat doar o proba,proba sa fie de pe domeniul de definitie, ca sa aflam care functie e mai mare pentru acesta valoare.
Aflind proba, demonstram ca pe intreg intervalul definit cutarea functie este > ca cealalta functie.
Am luat anticvariatul deoarece este foarte simplu, compact.
Ce sa mai scriu formularai, daca foarte bine a mers cu aceasta functie. Demonstratiile au mers. Daca insa, nu mergeau, atunci intradevar trebuia sa apelez la alte functii.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 19:29, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
" Daca nu ai sti de existenta acelor functii, cum ai demonstra acele conjecturi ? "
Buna intrebare.
Absolut idee nu am cum.
Cu jumatate de an in urma, intimplator, am aflat ca exsista pe lumea aceasta asa bogatii. Peste putin timp, poc-poc si ideile au venit.
Vezi acum ce inseamna vorba: "Omul informat este puternic" ?!
" Eu stiu ca se pot demonstra pe baza acestor functii care calculeaza numarul de numere prime, dar dupa cum vezi, nicaieri nu sunt acceptate acest tip de demonstratii. "
Ele nu calculeaza exsact, ci aproximeaza. Aici e marea diferenta.
Demonstratile cutare nu le-am analizat (cum sau obtinut cutarele functii), dar, cred ca de le-as analiza imi sar in cap o multime de notiuni neclare. Si, nici nu vreau sami bat capul [cu toate ca, unui cercetator de matematica, ii este interzis asa prostii de facut. Aceasta este o eroare de logica enorm de grava ]
" Mai nou, am citit undeva ca s-a demonstrat o functie care genereaza numerele prime, dar si aici este vorba tot despre o aproximare bazata tot pe logaritmul natural. "
Genereaza exsact numerele prime, sau arata distribitia lor (aproximeaza)?! Nu cred ca in scurt timp se vor gasi aceasta functie (sfinta).
Totus nu is deacord cu tine vizavi de aceea ca ar fi gresite acele functii care aproximeaza functia numerelor prime, adica spun de:
\leq \pi (x)\leq M(x))
Daca se spune ca cutarele a demonstrat, credc' asa si este.
Unicul mod de al contrazice in mod stiintific, e sa ii intelegem demonstratiile celui ce a dedus cutarele functii, si daca observam greseala tocmai atunci sa o expunem.
Presupun ca iti pare rau ca as fi luat-o pe dinainte cu conjecturelele alea. Nu lua in seama. Am lucrat si eu ceva timp (nu saga).
Ia sa cauti si sa vezi, cine au fost profesorii (sau in ce scoli ale lumii) invatatilor?!
Au fost profesori mari. Desigur mai este nevoe si de o munca personala enorma, insa fara o baza buna, cred ca doar roata vei reinventa, aceasta insa pe nimeni nu il intereseaza.
Nici eu nu is pe departe buricul, ba, nici materia de pina la clasa a XII nu o stiu complet.
Buna intrebare.
Absolut idee nu am cum.
Cu jumatate de an in urma, intimplator, am aflat ca exsista pe lumea aceasta asa bogatii. Peste putin timp, poc-poc si ideile au venit.
Vezi acum ce inseamna vorba: "Omul informat este puternic" ?!
" Eu stiu ca se pot demonstra pe baza acestor functii care calculeaza numarul de numere prime, dar dupa cum vezi, nicaieri nu sunt acceptate acest tip de demonstratii. "
Ele nu calculeaza exsact, ci aproximeaza. Aici e marea diferenta.
Demonstratile cutare nu le-am analizat (cum sau obtinut cutarele functii), dar, cred ca de le-as analiza imi sar in cap o multime de notiuni neclare. Si, nici nu vreau sami bat capul [cu toate ca, unui cercetator de matematica, ii este interzis asa prostii de facut. Aceasta este o eroare de logica enorm de grava ]
" Mai nou, am citit undeva ca s-a demonstrat o functie care genereaza numerele prime, dar si aici este vorba tot despre o aproximare bazata tot pe logaritmul natural. "
Genereaza exsact numerele prime, sau arata distribitia lor (aproximeaza)?! Nu cred ca in scurt timp se vor gasi aceasta functie (sfinta).
Totus nu is deacord cu tine vizavi de aceea ca ar fi gresite acele functii care aproximeaza functia numerelor prime, adica spun de:
Daca se spune ca cutarele a demonstrat, credc' asa si este.
Unicul mod de al contrazice in mod stiintific, e sa ii intelegem demonstratiile celui ce a dedus cutarele functii, si daca observam greseala tocmai atunci sa o expunem.
Presupun ca iti pare rau ca as fi luat-o pe dinainte cu conjecturelele alea. Nu lua in seama. Am lucrat si eu ceva timp (nu saga).
Ia sa cauti si sa vezi, cine au fost profesorii (sau in ce scoli ale lumii) invatatilor?!
Au fost profesori mari. Desigur mai este nevoe si de o munca personala enorma, insa fara o baza buna, cred ca doar roata vei reinventa, aceasta insa pe nimeni nu il intereseaza.
Nici eu nu is pe departe buricul, ba, nici materia de pina la clasa a XII nu o stiu complet.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 19:29, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 19:29, editata de 2 ori (Motiv : Am sters formula de inceput. Am scris intr-un notepad adresat altor persoane si am uitat sa sterg adresarea. :-))
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 19:29, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
privitor la penultimul tau mesaj- Am mult de obectat, si multe nu imi sunt clare.
Eu nu prea ma ocup cu rezolvarea altor probleme pe care eu nu mi le impun.
privitor la ultimul mesaj- da, e greu, si nici nu stiu cum (de stieam nici nu spuneam ca nu am aprofundat demonstratiile lui P.D.) prin metode elementare sa demonstrezi postulatul lui Bertran, darimite sa obtii acele functii ale lui PD.
Insa, tzac-tzac, cu un copy-paste, furindule, si facind ceva calcule, desigur e usor si nu e cinstit .
.

Eu am spus doar, ca nimic cine stie ce nu e, acestea strict rezulta din cutarele rezultate obtinute de altii.
Eu nu prea ma ocup cu rezolvarea altor probleme pe care eu nu mi le impun.
privitor la ultimul mesaj- da, e greu, si nici nu stiu cum (de stieam nici nu spuneam ca nu am aprofundat demonstratiile lui P.D.) prin metode elementare sa demonstrezi postulatul lui Bertran, darimite sa obtii acele functii ale lui PD.
Insa, tzac-tzac, cu un copy-paste, furindule, si facind ceva calcule, desigur e usor si nu e cinstit
Eu am spus doar, ca nimic cine stie ce nu e, acestea strict rezulta din cutarele rezultate obtinute de altii.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 19:29, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
Ai spus ca daca se rezolva conjectura lui Oppermann atunci valideaza si conjectura lui Andrica.
Cum, de ce?! Imi e foarte interesant, daca da, atunci pot sa fiu vesel o bucata de timp.
Eu inca nu am prins firul si nu mam concentrat sa fac asa legaturi, dar, nu cred, invers da, adica din Andrica=>Operman, poate fi.
Conjectura lui Andrica, fata de alte conjecturele, este una "puternica". La fel, in asa contexte, conjectura lui Firozbact e una "puternica", se pare chiar mai puternica ca a lui Andrica. Eu am incercat, dar, numai la mijlocuri de drumuri am ajuns , mai tirziu voi arata pacalelile(sunt si ele interesant, mai ales erorile [erorile diochete, mi se pare ca sunt cele mai interesante, mai interesante ca orice]).
Cum, de ce?! Imi e foarte interesant, daca da, atunci pot sa fiu vesel o bucata de timp.
Eu inca nu am prins firul si nu mam concentrat sa fac asa legaturi, dar, nu cred, invers da, adica din Andrica=>Operman, poate fi.
Conjectura lui Andrica, fata de alte conjecturele, este una "puternica". La fel, in asa contexte, conjectura lui Firozbact e una "puternica", se pare chiar mai puternica ca a lui Andrica. Eu am incercat, dar, numai la mijlocuri de drumuri am ajuns , mai tirziu voi arata pacalelile(sunt si ele interesant, mai ales erorile [erorile diochete, mi se pare ca sunt cele mai interesante, mai interesante ca orice]).
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 19:30, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
M-am supra incarcat cu o multime de lucruri (multe care abea am inceput sa le postez..), si deaceea multe din neatentie pot sa le scap acum, dar daca nu ma incarc in alte directii in viitor, as veni in scurt timp cu raspunsuri interesante.
Se pare, ca asa e, eu prea nu am pretuit la justa valoare conjecturelele lui Schinzel si mai ales a lui Oppermann.
Se pare ca asa este, exista lecaturi, cea a lui Oppermann fiind deasupra chiar si pe a lui Andrica.
Am ceva de spus la cea a lui Andrica, ce nu trebue de facut, ce greseli sa nu sa se faca cum eu am facut, aplicind functia minim in anumite consensuri.Pina la urma, nu am rezistat provocarii .
.
[is incarcat, deaceea pot comite si erori]
Mi-am dat seama azi ziua.. facind o substitutie de variabila , nu avem nimic altceva decit conjectura lui Schinzel.
, nu avem nimic altceva decit conjectura lui Schinzel.
In conjectura lui Oppermann am dedus caci valoarea minima a lui trebue sa fie
trebue sa fie 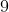 , vom avea deci:
, vom avea deci:  .
.
Insa, conjectura lui Schinzel spune ca: , deci ceva am luat-o prin aratura.
, deci ceva am luat-o prin aratura.
Posibil, am comis greseluta pe la anticvariat, sau pe la substitutii [trebue de mai revenit la Oppermann, si de lustrit mai bine, insa nu e nimic grav]
Andrica:
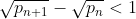
Acesta inseamna:

adica

 este al n-ulea numar prim. Insa perfect de bine merge si pentru cazul cind este un oarecare numar natural.
este al n-ulea numar prim. Insa perfect de bine merge si pentru cazul cind este un oarecare numar natural.
Adica, bine mersi mege si asa:

unde
In acest caz, din conjectura lui Schinzel indata => caci conjectura lui Andrica este adevarata daca si conjectura lui Schinzel este adevarata.
Se pare, ca asa e, eu prea nu am pretuit la justa valoare conjecturelele lui Schinzel si mai ales a lui Oppermann.
Se pare ca asa este, exista lecaturi, cea a lui Oppermann fiind deasupra chiar si pe a lui Andrica.
Am ceva de spus la cea a lui Andrica, ce nu trebue de facut, ce greseli sa nu sa se faca cum eu am facut, aplicind functia minim in anumite consensuri.Pina la urma, nu am rezistat provocarii
 .
.[is incarcat, deaceea pot comite si erori]
Mi-am dat seama azi ziua.. facind o substitutie de variabila
In conjectura lui Oppermann am dedus caci valoarea minima a lui
Insa, conjectura lui Schinzel spune ca:
Posibil, am comis greseluta pe la anticvariat, sau pe la substitutii [trebue de mai revenit la Oppermann, si de lustrit mai bine, insa nu e nimic grav]
Andrica:
Acesta inseamna:
adica
Adica, bine mersi mege si asa:
unde
In acest caz, din conjectura lui Schinzel indata => caci conjectura lui Andrica este adevarata daca si conjectura lui Schinzel este adevarata.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
Acum ar ramine Smarandache.
Ce mai concret drebue de demonstrat?! Ma poate cineva lamuri concret?!
Trebue de demonstrat ca anume exsista o an umita constanta care respecta egalitatea cutare, ea fiind anume cel ce el a spus ~0.56.., adica sa o cuprindem in un anumit interval ?!
Daca da, atunci se poate si nu e cine stie ce.
Demonstram ca exsista o anumita constanta coprinsa in un anumit interval, sa nu facem multa zarva, aratam ce se intimpla cind x=0.5 (deja stim) si cind x=0.6. Astfel aratam ca exsista o anumita valoare cuprinsa intre (0.5;0.6) (unica- trebuesc si aici ceva demonstratii) pentru care se respecta egalitatea, deci demonstram conjectura.
Calea de demonstrare e aproape totalment scrisa dea gata pe aici.
Ce mai concret drebue de demonstrat?! Ma poate cineva lamuri concret?!
Trebue de demonstrat ca anume exsista o an umita constanta care respecta egalitatea cutare, ea fiind anume cel ce el a spus ~0.56.., adica sa o cuprindem in un anumit interval ?!
Daca da, atunci se poate si nu e cine stie ce.
Demonstram ca exsista o anumita constanta coprinsa in un anumit interval, sa nu facem multa zarva, aratam ce se intimpla cind x=0.5 (deja stim) si cind x=0.6. Astfel aratam ca exsista o anumita valoare cuprinsa intre (0.5;0.6) (unica- trebuesc si aici ceva demonstratii) pentru care se respecta egalitatea, deci demonstram conjectura.
Calea de demonstrare e aproape totalment scrisa dea gata pe aici.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 19:30, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
Se aduce la cunoştinţa unui administrator acest lucru, iar restul este treaba acestuia. Doreşti un forum personal?
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 19:30, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 19:30, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 19:30, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
Ce parere aveti vizavi de rezolvarea celor 5 conjecturi: legendre,brocard,schinzel,operman,andrica ?!
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 19:30, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
altii, altii, parerea ????????
repejor, care este parerea, sunt valide sau nu rezolvarile ?!
repejor, care este parerea, sunt valide sau nu rezolvarile ?!
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 19:30, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
Nu mis clare multe lucruri aici.
La ce te-ai referit cind ai scris deltaM(x), delta m(x) ?!
Cu ce ele ajuta la rezolvarea conjecturilor.
Inegalitatile sunt adevarate, deoarece:
Atit functiile M(x) cit si m(x) sunt crescatoare si convexe, deci dupa un numar suficient de mare inegalitatea este adevarata pe domeniul ei de definitie.
Diferentele alea, formeaza niste termeni care sunt permament convergenti.
Din cite tin minte la fel se intimpla si cu radicalul din acele functii. La fel cind ii punem sub radical, la fel vom avea functii crescatoare convexe, la fel dupa un numar suficient de mare, inegalitatile sunt adevarate pe domeniul lor de definitie.
La ce te-ai referit cind ai scris deltaM(x), delta m(x) ?!
Cu ce ele ajuta la rezolvarea conjecturilor.
Inegalitatile sunt adevarate, deoarece:
Atit functiile M(x) cit si m(x) sunt crescatoare si convexe, deci dupa un numar suficient de mare inegalitatea este adevarata pe domeniul ei de definitie.
Diferentele alea, formeaza niste termeni care sunt permament convergenti.
Din cite tin minte la fel se intimpla si cu radicalul din acele functii. La fel cind ii punem sub radical, la fel vom avea functii crescatoare convexe, la fel dupa un numar suficient de mare, inegalitatile sunt adevarate pe domeniul lor de definitie.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
meteor a scris prin forumul său :
"^{i}C^{i}_{x}(x-i+1)^{x}=\sum_{i=0}^{2x}C_{2x}^{i}(2x-i+1)^{x}-\left ( \sum_{i=0}^{2x+1}C_{2x+1}^{i}(2x-i+2)^{x}\right ) ,\forall x\geq 0) "
"
Mie mi se pare mult, muult, muuult mai simplu aşa :
\cdot x=\prod_{i=1}^{x}i})
adică definiţia clasică a factorialului.
Şi nu cred că numai pentru mine, ci pentru oricine altcineva.
A fi un bun matematician înseamnă, printre altele, să poţi aduce la o formă cât mai simplă o situaţie ce pare a fi complicată, nu să o complici şi mai mult.
Ori prea multă "chinezăreală" oboseşte mintea repede.
"
Mie mi se pare mult, muult, muuult mai simplu aşa :
adică definiţia clasică a factorialului.
Şi nu cred că numai pentru mine, ci pentru oricine altcineva.
A fi un bun matematician înseamnă, printre altele, să poţi aduce la o formă cât mai simplă o situaţie ce pare a fi complicată, nu să o complici şi mai mult.
Ori prea multă "chinezăreală" oboseşte mintea repede.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
Scopul meu este sa rezolv factorialul din o lovitura, sa gasesc acea formula. Cica este ceva cu Gamma functia, insa o las pina ce la o parte.
Spre exemplu ca sa calculez 100! (un numar foarte mare ce este drept), numai inlocuid 100 in cutarea formula, si indata sa imi dea raspunsul, nu sa inmultesc de la 2 la 100.
Adesea rezolvarea problemelor e ca si cum ai deznoda un nod mare, trebue intii de toate sa il desfaci si desfaci, si apoi sa il deznozi, ce e drept nu de fiecare data e cu succes.
Aceolo ce sa facut "ceva-ceva" e ca am "rupt" factorialul din produs in sume.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
In acele formule ale factorialului trebuie să calculezi în final nişte combinări care sunt de fapt după simplificare nişte produse de numere consecutive şi aceste produse se înmulţesc cu numărul din paranteza aia şi apoi să faci suma algebrică a acestor ultime produse.....Cam complicat,dar sigur că este interesantă prima formulă a lui  care trebuie totuşi demonstrată.In formula a doua aceluiaşi
care trebuie totuşi demonstrată.In formula a doua aceluiaşi  cine este
cine este  ?
? 
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Despre forumul personal al lui meteor
Re: Despre forumul personal al lui meteor
n, este un oarecare numar natural care tu doresti, mai mare sau egal ca k.
banal, nu?!
Nu e nimic insa banal.
banal, nu?!
Nu e nimic insa banal.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
Pagina 1 din 2 • 1, 2 
 Subiecte similare
Subiecte similare» Discuții despre subiectele din forumul lui meteor
» De ce forumul personal?!
» pareri despre subiectul anunt personal
» De ce forumul personal?!
» pareri despre subiectul anunt personal
Pagina 1 din 2
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 
