Ultimele subiecte
» Ce anume "generează" legile fizice?Scris de CAdi Astazi la 15:57
» Dovezi ce atestă existența lui DUMNEZEU și că EL este UNICUL CREATOR al Universului
Scris de Forever_Man Astazi la 15:37
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de CAdi Astazi la 12:13
» În ce tip de dovezi aveţi încredere deplină?
Scris de Forever_Man Ieri la 21:41
» Unde a ajuns stiinta ?
Scris de virgil Ieri la 18:02
» Ce fel de popor suntem
Scris de virgil Ieri la 17:40
» Eu sunt Dumnezeu - viitoarea mea carte in limba romana
Scris de Forever_Man Dum 24 Noi 2024, 09:16
» ChatGPT este din ce în ce mai receptiv
Scris de Meteorr Sam 23 Noi 2024, 21:12
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 1 )
» Mesaj de la eugen în Ce fel de popor suntem
( 1 )
» Mesaj de la CAdi în OZN in Romania
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12466) | ||||
| CAdi (12404) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7964) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3970) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| Forever_Man | ||||
| Dacu2 | ||||
| Meteorr | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 17 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 17 Vizitatori :: 1 Motor de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Determinarea diferentei maxime dintre doua numere prime consecutive
Pagina 1 din 1
 Determinarea diferentei maxime dintre doua numere prime consecutive
Determinarea diferentei maxime dintre doua numere prime consecutive
Ar putea fi mai multe metode. Care imi apar, le voi spune pe rind.
Ce e important, este de determinat cit posibil mai corect, aceasta, va permite rezolvare a o sumedenie de probleme cel putin din cadrul teoriei numerelor prime.
Ce e important, este de determinat cit posibil mai corect, aceasta, va permite rezolvare a o sumedenie de probleme cel putin din cadrul teoriei numerelor prime.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25855
Data de inscriere : 19/06/2011
 Re: Determinarea diferentei maxime dintre doua numere prime consecutive
Re: Determinarea diferentei maxime dintre doua numere prime consecutive
Prima metoda, este de a aplica functiile minim si maxim.
Iata desenul, care spune totul, insa voi comenta ca sa se digere mai bine informatia.

A determina distanta maxima dintre 2 numere prime consecutive este aceeasi cum al determina pe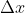 din ecuatia:
din ecuatia:
-M(x)=1)
Daca insa sa fim ceva mai rigurosi, si a scrie mai corect, ar trebui asa sa fie:
![[m(x+\Delta x)]-[M(x)]=1](http://latex.codecogs.com/gif.latex?[m(x+\Delta x)]-[M(x)]=1)
sau
![[m(p_{x}+\Delta p_{x})]-[M(p_{x})]=1\Rightarrow \Delta p_{x}=...](http://latex.codecogs.com/gif.latex?[m(p_{x}+\Delta p_{x})]-[M(p_{x})]=1\Rightarrow \Delta p_{x}=...)
Determinarea deltei din asa ecuatii, deseori (cind functiile minim si maxim au o forma diocheata) nu mi se pare un lucru deloc usor.
Insa, in dependenta de problema, posibil s-ar putea evita conditia de al determina pe delta.
Spre exemplu daca dorim sa rezolvam conjectura lui Andrica (cu anumite functii minim si maxim, cu conditia ca l-am determinat pe delta) vom avea:
![\sqrt{[m(p_{x}+\Delta p_{x})]}-\sqrt{[M(p_{x})]}<1](http://latex.codecogs.com/gif.latex?\sqrt{[m(p_{x}+\Delta p_{x})]}-\sqrt{[M(p_{x})]}<1)
Insa, din cauza ca avem functiile minim si maxim slabanoage, putem avea chiar contrariul:
![\sqrt{[m(p_{x}+\Delta p_{x})]}-\sqrt{[M(p_{x})]}\geq 1](http://latex.codecogs.com/gif.latex?\sqrt{[m(p_{x}+\Delta p_{x})]}-\sqrt{[M(p_{x})]}\geq 1)
[repet, aceasta cred ca se intimpla nu din cauza ca demersul logic e gresit, ci din cauza caci functiile slab aproximeaza]
Iata desenul, care spune totul, insa voi comenta ca sa se digere mai bine informatia.

A determina distanta maxima dintre 2 numere prime consecutive este aceeasi cum al determina pe
Daca insa sa fim ceva mai rigurosi, si a scrie mai corect, ar trebui asa sa fie:
sau
Determinarea deltei din asa ecuatii, deseori (cind functiile minim si maxim au o forma diocheata) nu mi se pare un lucru deloc usor.
Insa, in dependenta de problema, posibil s-ar putea evita conditia de al determina pe delta.
Spre exemplu daca dorim sa rezolvam conjectura lui Andrica (cu anumite functii minim si maxim, cu conditia ca l-am determinat pe delta) vom avea:
Insa, din cauza ca avem functiile minim si maxim slabanoage, putem avea chiar contrariul:
[repet, aceasta cred ca se intimpla nu din cauza ca demersul logic e gresit, ci din cauza caci functiile slab aproximeaza]
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25855
Data de inscriere : 19/06/2011
 Re: Determinarea diferentei maxime dintre doua numere prime consecutive
Re: Determinarea diferentei maxime dintre doua numere prime consecutive
Ultima editare efectuata de catre meteor in Mier 06 Feb 2013, 23:30, editata de 1 ori
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25855
Data de inscriere : 19/06/2011
 Re: Determinarea diferentei maxime dintre doua numere prime consecutive
Re: Determinarea diferentei maxime dintre doua numere prime consecutive
[neverificat si nedemonstrat pina la capat!] Pentru ca sa marim aproximatiile functiilor minim/maxim, sa le facem suficient de puternice astfel incit sa ne permita sa calculam anumite probleme, se poate asa [nu mai fac desene si nu mai aduc calcule ca imi va lua timp, daca cineva nu ii clar, poate intreba]:
-Intii de toate eu as prefera sa lucrez cu functia lui Legendre, este destul de comoda si compacta, s-a demonstrat si definit, care intersecteaza functia numerelor prime, si contine o anumita constanta (nedefinita pina la capat, ma refer la zecimale):
=\frac{x}{ln(x)-1.08366..}) .
.
Aceasta constanta e notata cu (cum am mai scris, care incepe cu
(cum am mai scris, care incepe cu  )
)
Aceasta precizie a constantei, face ca functia lui Legendre sa intersecteze functia numerelor prime pina la o anumita valoare, apoi sare in sus, si hatu nu mai revine.
O idee de grota [ne rigid demonstrata], e sa incapem sa vinam cit mai multe zecimale a acestei constante [mai apoi se va vedea simplu ca e foarte importanta].
Dacadupa o anumita valoare functia sare deasupra functiei numerelor prime, inseamna ca trebue ca sa marim cu o anumita valoare constanta. Dupa ultima cifra poate fi 0,1,2,..,9. Problema e daca e 0. Si mai problematic e daca la fel s-ar intimpla cu vreo nu se stie cite zecimale de zero, si tocmai apoi sa vina o cifra diferita de zero. Marirea preciziei constantei cu o zecimala e batae de cap si trebue sa pui calculatorul in miscare, daap vreo douazeci.
Ideea deci e asa: Adaugam 1 la ultima cifra a constante, daca functia nu sare in sus, inseamna ca este o valoare intre 0 si 1. Daca, la adaugarea lui 1 functia tot sta in sus, inseamna ca 1 nu e bun, si trebue de inlocuit cu 2, etc. verificam pina la 9.
Apoi trecem la urmatoarea zecimala (in dependenta de putinte), etc.
- Dupa ce aproximam mai bine constanta B , deci aproximam functia Le(x) mai bine, putem trece la urmatorul pas, si anume a transforma functia Le(x) in m(x) si M(x), de remarcat ca acestea vor aproxima fenomenal de bine functia PI(x).
Cum sa facem ca din Le(x) sa facem si m(x) si M(x) ?!
Prin translatii si prin rotatii.
Dupa ce definim ca functia pina la o anumita valoare intersecteaza functia numerelor prime, si demonstram apoi ca dupa o anumita valoare [desigur mai mare] functia Le(x) sare in sus/ sau/ jos [ca.. nus' cind il vor defini total pe constanta B, caci presupun no' fi asa usor] :
- functia M(x) este o translatia a functiei Le(x) cu citeva unitati [fie ii spunem cu k,t unitati] (nu cred caci k,t e mai mult de 2) spre stinga-sus [se poate pur si simplu spre stinga, sau sus, depinde de cum se determina ca e mai bine], aceasta inseamna: M(x)=Le(x-k)+t.
- insa, pentru ca sa obtinem functia m(x), este nevoe ca sa aflam dupa ce valoare Le(x) sare peste PI(x) [determinam pentru o anumita valoare cu cit sare peste] sa rotim functia Le(x) cu un unghi [sau..se pote sa ne amestecam la constanta B, adica sa o facem putin mai mare, astfel incit dupa o anumita valoare mare, functia Le(x) sa plece strict sub PI(x)] care sa o faca pe Le(x), dupa o anumita valoare (peste sute de miliarde) sa fie vesnic sub PI(x). Apoi ii facem o translatie spre dreapta-jos [se poate pur si simplu spre dreapta, sau jos, depinde de cum se determina ca e mai bine], si poftim m(x)=Le(x+k)-t.
Rotatiile nu prea le sfatui, deoarece apar functiile trigonometrice, apar niste formule ca iti cad urechile doar vazindule, mai mult, lucrul cu functiile trigonometrice [problema mileniilor] nu e un lucru comod.
Obtinerea noilor functii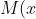) si
si 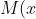) ar fi cu muult mai puternice ca cele din ziua de az, fie sa zicem cele ale lui P.D. (aici le notez:
ar fi cu muult mai puternice ca cele din ziua de az, fie sa zicem cele ale lui P.D. (aici le notez: ) si
si ) )
)
Adica asa ar iesi ca:
_{x\geq \lambda '}\leq m(x)_{x\geq \lambda } \leq \pi (x)\leq M(x)_{x\geq \nu }\leq M'(x)_{x\geq \lambda '})
-Intii de toate eu as prefera sa lucrez cu functia lui Legendre, este destul de comoda si compacta, s-a demonstrat si definit, care intersecteaza functia numerelor prime, si contine o anumita constanta (nedefinita pina la capat, ma refer la zecimale):
Aceasta constanta e notata cu
Aceasta precizie a constantei, face ca functia lui Legendre sa intersecteze functia numerelor prime pina la o anumita valoare, apoi sare in sus, si hatu nu mai revine.
O idee de grota [ne rigid demonstrata], e sa incapem sa vinam cit mai multe zecimale a acestei constante [mai apoi se va vedea simplu ca e foarte importanta].
Dacadupa o anumita valoare functia sare deasupra functiei numerelor prime, inseamna ca trebue ca sa marim cu o anumita valoare constanta. Dupa ultima cifra poate fi 0,1,2,..,9. Problema e daca e 0. Si mai problematic e daca la fel s-ar intimpla cu vreo nu se stie cite zecimale de zero, si tocmai apoi sa vina o cifra diferita de zero. Marirea preciziei constantei cu o zecimala e batae de cap si trebue sa pui calculatorul in miscare, daap vreo douazeci.
Ideea deci e asa: Adaugam 1 la ultima cifra a constante, daca functia nu sare in sus, inseamna ca este o valoare intre 0 si 1. Daca, la adaugarea lui 1 functia tot sta in sus, inseamna ca 1 nu e bun, si trebue de inlocuit cu 2, etc. verificam pina la 9.
Apoi trecem la urmatoarea zecimala (in dependenta de putinte), etc.
- Dupa ce aproximam mai bine constanta B , deci aproximam functia Le(x) mai bine, putem trece la urmatorul pas, si anume a transforma functia Le(x) in m(x) si M(x), de remarcat ca acestea vor aproxima fenomenal de bine functia PI(x).
Cum sa facem ca din Le(x) sa facem si m(x) si M(x) ?!
Prin translatii si prin rotatii.
Dupa ce definim ca functia pina la o anumita valoare intersecteaza functia numerelor prime, si demonstram apoi ca dupa o anumita valoare [desigur mai mare] functia Le(x) sare in sus/ sau/ jos [ca.. nus' cind il vor defini total pe constanta B, caci presupun no' fi asa usor] :
- functia M(x) este o translatia a functiei Le(x) cu citeva unitati [fie ii spunem cu k,t unitati] (nu cred caci k,t e mai mult de 2) spre stinga-sus [se poate pur si simplu spre stinga, sau sus, depinde de cum se determina ca e mai bine], aceasta inseamna: M(x)=Le(x-k)+t.
- insa, pentru ca sa obtinem functia m(x), este nevoe ca sa aflam dupa ce valoare Le(x) sare peste PI(x) [determinam pentru o anumita valoare cu cit sare peste] sa rotim functia Le(x) cu un unghi [sau..se pote sa ne amestecam la constanta B, adica sa o facem putin mai mare, astfel incit dupa o anumita valoare mare, functia Le(x) sa plece strict sub PI(x)] care sa o faca pe Le(x), dupa o anumita valoare (peste sute de miliarde) sa fie vesnic sub PI(x). Apoi ii facem o translatie spre dreapta-jos [se poate pur si simplu spre dreapta, sau jos, depinde de cum se determina ca e mai bine], si poftim m(x)=Le(x+k)-t.
Rotatiile nu prea le sfatui, deoarece apar functiile trigonometrice, apar niste formule ca iti cad urechile doar vazindule, mai mult, lucrul cu functiile trigonometrice [problema mileniilor] nu e un lucru comod.
Obtinerea noilor functii
Adica asa ar iesi ca:
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25855
Data de inscriere : 19/06/2011
 Re: Determinarea diferentei maxime dintre doua numere prime consecutive
Re: Determinarea diferentei maxime dintre doua numere prime consecutive
Mai... daca nu ati ametit voi, atunci eu se pare ca da 
Problema [din ciclu primar ]:
- Fie avem un anumit sir de numere (numere prime), la care termenii se afla in ordine crescatoare insa la care nu se stie nimic absolut despre succesivitatea terminilor sirului (nu se cunoaste nici o regula de aparitie a terminilor), INSA se stie cert caci:
De la la
la  (
( apartine domeniului de definitie al functiei care il aplica,
apartine domeniului de definitie al functiei care il aplica,  ) sunt cel putin
) sunt cel putin ) numere prime.
numere prime.
De la la
la  sunt cel putin
sunt cel putin ) numere prime.
numere prime.
-Intrebare:
Este corect sau nu, caci:
Intre si
si  sunt cel putin
sunt cel putin -f(x)) numere prime ???????????
numere prime ???????????
Pare destul de evident ca este corect nici vorba, INSA sunt doua neclaritati:
-Este corect oare a aplica acest principiu in cazul in care termenii sirului nu au (nu li se cunoaste) o ordine?!
-Din graficele acestor functii (numerelor prime si functiei minim), am observat(presupus) caci s-ar putea sa fie contraexemple. Numai am presupus, nu am demonstrat nimic, nici da nici nu.
In cazul in care, se va da unda verde caci este foarte corect a aplica acesta concluzie ( caci numarul minim de numere prime in acel interval este de-f(x)) ), adica nu mai este nevoe sa inventam bicicleta cu 5 roti daca este cea cu 2 roti, in asa caz cad rezolvate brusc sute de probleme din acest domeniu al matematicii.
), adica nu mai este nevoe sa inventam bicicleta cu 5 roti daca este cea cu 2 roti, in asa caz cad rezolvate brusc sute de probleme din acest domeniu al matematicii.
In caz contrar, suntem nevoiti sa lasam acest drum.
Problema [din ciclu primar ]:
- Fie avem un anumit sir de numere (numere prime), la care termenii se afla in ordine crescatoare insa la care nu se stie nimic absolut despre succesivitatea terminilor sirului (nu se cunoaste nici o regula de aparitie a terminilor), INSA se stie cert caci:
De la
De la
-Intrebare:
Este corect sau nu, caci:
Intre
Pare destul de evident ca este corect nici vorba, INSA sunt doua neclaritati:
-Este corect oare a aplica acest principiu in cazul in care termenii sirului nu au (nu li se cunoaste) o ordine?!
-Din graficele acestor functii (numerelor prime si functiei minim), am observat(presupus) caci s-ar putea sa fie contraexemple. Numai am presupus, nu am demonstrat nimic, nici da nici nu.
In cazul in care, se va da unda verde caci este foarte corect a aplica acesta concluzie ( caci numarul minim de numere prime in acel interval este de
In caz contrar, suntem nevoiti sa lasam acest drum.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25855
Data de inscriere : 19/06/2011
 Re: Determinarea diferentei maxime dintre doua numere prime consecutive
Re: Determinarea diferentei maxime dintre doua numere prime consecutive
---==Distanta maxima dintre 2 numere prime consecutive fata de altele, sau -raportata la ele==---

[sper ca nu e gresita notatia si exprimarea, ?!]
Din aceasta formula observam ca distanta maxima dintre 2 numere prime consecutive fata de altele este intre:
3 si 5.
In orice caz asa e ordinea:
(3,5); (7,11); (2,3); ...
[sper ca nu e gresita notatia si exprimarea, ?!]
Din aceasta formula observam ca distanta maxima dintre 2 numere prime consecutive fata de altele este intre:
3 si 5.
In orice caz asa e ordinea:
(3,5); (7,11); (2,3); ...
Ultima editare efectuata de catre meteor in Mar 05 Mar 2013, 09:33, editata de 1 ori
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25855
Data de inscriere : 19/06/2011
 Re: Determinarea diferentei maxime dintre doua numere prime consecutive
Re: Determinarea diferentei maxime dintre doua numere prime consecutive
---===Raportul minim intre 2 numere prime consecutive==---
Este:

[ Despre raportul maxim intre 2 numere prime consecutive nici nu ne intereseaza, caci in cazul in care numerele gemene is infinite, pentru valorile cind tind la infinit, raportul tinde catre 1 ]
Se observa deci ca raportul este minim atunci cind distanta dintre si
si 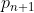 este maxima, insa in dependenta de un anumit referential (adica de
este maxima, insa in dependenta de un anumit referential (adica de  ).
).
La fel banui ca raportul minim este in ordinea ca in cazul enumerat mai sus:
(3,5); (7,11); (2,3); ...
Este:
[ Despre raportul maxim intre 2 numere prime consecutive nici nu ne intereseaza, caci in cazul in care numerele gemene is infinite, pentru valorile cind tind la infinit, raportul tinde catre 1 ]
Se observa deci ca raportul este minim atunci cind distanta dintre
La fel banui ca raportul minim este in ordinea ca in cazul enumerat mai sus:
(3,5); (7,11); (2,3); ...
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25855
Data de inscriere : 19/06/2011
 Subiecte similare
Subiecte similare» Raportul a două numere naturale prime consecutive.
» Ecuaţie cu trei numere prime consecutive
» Suma aritmetica a primelor n numere prime consecutive
» Ecuaţie cu trei numere prime consecutive
» Suma aritmetica a primelor n numere prime consecutive
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 