Ultimele subiecte
» Ce anume "generează" legile fizice?Scris de Forever_Man Astazi la 17:44
» Dovezi ce atestă existența lui DUMNEZEU și că EL este UNICUL CREATOR al Universului
Scris de Forever_Man Astazi la 15:37
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de CAdi Astazi la 12:13
» În ce tip de dovezi aveţi încredere deplină?
Scris de Forever_Man Ieri la 21:41
» Unde a ajuns stiinta ?
Scris de virgil Ieri la 18:02
» Ce fel de popor suntem
Scris de virgil Ieri la 17:40
» Eu sunt Dumnezeu - viitoarea mea carte in limba romana
Scris de Forever_Man Dum 24 Noi 2024, 09:16
» ChatGPT este din ce în ce mai receptiv
Scris de Meteorr Sam 23 Noi 2024, 21:12
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
Postări cu cele mai multe reacții ale lunii
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la No_name în Ce anume "generează" legile fizice?
( 1 )
» Mesaj de la Forever_Man în Eu sunt Dumnezeu - viitoarea mea carte in limba romana
( 1 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12466) | ||||
| CAdi (12404) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7964) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3970) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| Forever_Man | ||||
| ilasus | ||||
| Dacu2 | ||||
| Meteorr | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 20 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 20 Vizitatori Nici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Calculul solutiilor ecuatiilor (deasemeni atentie speciala la ec. de grad mai mare ca 4)
Pagina 1 din 1
 Calculul solutiilor ecuatiilor (deasemeni atentie speciala la ec. de grad mai mare ca 4)
Calculul solutiilor ecuatiilor (deasemeni atentie speciala la ec. de grad mai mare ca 4)
A putea determina solutiile ecuatiei inseamna a intelege aproape totul in lumea stiintei.
Da desigur, ecuatiile se clasifica ca nu le vezi capatul:
- Calculul solutiilor ecuatiei in anumite submultimi/multimi (N, Q, R, C,..)
- Ecuatii cu o variabila, doua, trei, etc.
- Altele.
Eu prefer sa analizez mai detaliat aici:
- Determinarea solutiilor in R.
- Ecuatii cu o singura necunoscuta.
Da desigur, ecuatiile se clasifica ca nu le vezi capatul:
- Calculul solutiilor ecuatiei in anumite submultimi/multimi (N, Q, R, C,..)
- Ecuatii cu o variabila, doua, trei, etc.
- Altele.
Eu prefer sa analizez mai detaliat aici:
- Determinarea solutiilor in R.
- Ecuatii cu o singura necunoscuta.
Ultima editare efectuata de catre meteor in Dum 25 Aug 2013, 13:47, editata de 1 ori
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25855
Data de inscriere : 19/06/2011
 Re: Calculul solutiilor ecuatiilor (deasemeni atentie speciala la ec. de grad mai mare ca 4)
Re: Calculul solutiilor ecuatiilor (deasemeni atentie speciala la ec. de grad mai mare ca 4)
Prima metoda este de a aplica inversa functiei pe anumite intervale strict definite https://cercetare.forumgratuit.ro/t926-calculul-inversei-unei-functii-si-aplicatii-ale-acestei-inversatii, functia trebue sa fie continua si derivabila pe acest interval (cu toateca eu cred ca toate functiile sunt derivabile, pe anumite domenii unele insa avind derivate diferite..).
Insa aceasta metoda face batai de cap la moment cind vine vorba de calculul cutarei integrale.
Insa aceasta metoda face batai de cap la moment cind vine vorba de calculul cutarei integrale.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25855
Data de inscriere : 19/06/2011
 Re: Calculul solutiilor ecuatiilor (deasemeni atentie speciala la ec. de grad mai mare ca 4)
Re: Calculul solutiilor ecuatiilor (deasemeni atentie speciala la ec. de grad mai mare ca 4)
A doua metoda, totii o stiti. E simpla si clara, nimic uimitor, insa cred ca slabut aprofundata.
Limitele, calculul lor, in matematica e ceva si mai. Prin limite practic se poate de exprimat orice. Deseori sunt o bizarietate completa.
Care este ideea ?!
Ce inseamna derivata unei functii ?!
Derivata unei funcții semnifică rata cu care se modifică valoarea funcției atunci când se modifică argumentul.
Adica derivata inseamna o anumita functie care caracterizeaza functia mama, in ce mod are loc la ea raportul dintre cresterea functiei catre cresterea argumentului.
Retineti: Determinind felul cum ne apropiem de solutia ecuatiei, inseamna a determina o anumita functie (asimptota). Calculind limita aceasta noi gasim solutia ecuatiei.
Deaceea intii de toate am spus putin despre derivata, v-am facut o analogie, sa va imaginati cit mai bine care este miezul.
In ziua de azi se cunosc foarte larg trei metode (metoda coardelor, metoda bisectiei, metoda tangentelor) de calcul numeric a solutiei anumitei ecuatii (pentru anumita metoda, ecuatia trebue sa indeplineasca anumitele minime cerinte).
Cerintele care trebue sa le indeplineasca si ecuatiile care fac exceptie is ca negrul sub unghii (in ziua de az, in comparatie cu problemele care survin).
Daca, am determina un algoritm dupa care sa putem calcula solutiile anumitor ecuatii cu anumita metoda, atunci este foarte foarte bine.
Noi, cind calculam recursiv solutiile numerice ale acelei ecuatii, noi nu facem nimic alceva decit parcurgem o anumita functie in anumite puncte ale ei, care este asimptotica catre valoarea solutiei functiei in acel interval.
Acesta e nucleul.
Determinind aceasta functie, calculind aceasta limita, noi gasim solutia ecuatiei.
Asimptota, (si normal ca) ar trebui sa fie una orizontala.
Limitele, calculul lor, in matematica e ceva si mai. Prin limite practic se poate de exprimat orice. Deseori sunt o bizarietate completa.
Care este ideea ?!
Ce inseamna derivata unei functii ?!
Derivata unei funcții semnifică rata cu care se modifică valoarea funcției atunci când se modifică argumentul.
Adica derivata inseamna o anumita functie care caracterizeaza functia mama, in ce mod are loc la ea raportul dintre cresterea functiei catre cresterea argumentului.
Retineti: Determinind felul cum ne apropiem de solutia ecuatiei, inseamna a determina o anumita functie (asimptota). Calculind limita aceasta noi gasim solutia ecuatiei.
Deaceea intii de toate am spus putin despre derivata, v-am facut o analogie, sa va imaginati cit mai bine care este miezul.
In ziua de azi se cunosc foarte larg trei metode (metoda coardelor, metoda bisectiei, metoda tangentelor) de calcul numeric a solutiei anumitei ecuatii (pentru anumita metoda, ecuatia trebue sa indeplineasca anumitele minime cerinte).
Cerintele care trebue sa le indeplineasca si ecuatiile care fac exceptie is ca negrul sub unghii (in ziua de az, in comparatie cu problemele care survin).
Daca, am determina un algoritm dupa care sa putem calcula solutiile anumitor ecuatii cu anumita metoda, atunci este foarte foarte bine.
Noi, cind calculam recursiv solutiile numerice ale acelei ecuatii, noi nu facem nimic alceva decit parcurgem o anumita functie in anumite puncte ale ei, care este asimptotica catre valoarea solutiei functiei in acel interval.
Acesta e nucleul.
Determinind aceasta functie, calculind aceasta limita, noi gasim solutia ecuatiei.
Asimptota, (si normal ca) ar trebui sa fie una orizontala.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25855
Data de inscriere : 19/06/2011
 Re: Calculul solutiilor ecuatiilor (deasemeni atentie speciala la ec. de grad mai mare ca 4)
Re: Calculul solutiilor ecuatiilor (deasemeni atentie speciala la ec. de grad mai mare ca 4)
Sa incepem cu prima metoda - Metoda tangentelor (sau uneori se mai spune metoda lui Newton).
Felul cum se aplica aceasta metoda, usor se poate face analogii catre alte metode, sa spunem catre metoda coardelor. Cel mai important e sa iasa la suprafata odata si odata o metoda finisata.
Deasemenea, de retinut ca fiecare metoda (mai ales in calculul numeric) are avantajele si dezavantajele ei [V.S. a avut o idee, cica: sa aplicam succesiv toate trei metode. Ideea e una buna, deoarece aduna la un loc in primul rind avantajele. In un numar mai mic de pasi, ne putem apropia (in dependenta de caz..) mai rapid de solutia ecuatiei, fata de alte metode particulare].
Fie este o functie continua si derivabila pe intervalul![[A_{0};B_{0}]](http://latex.codecogs.com/gif.latex?[A_{0};B_{0}]) .
.
Fie pentru cazul nostru functia o notam cu) , si ea este concava crescatoare pe acest interval.
, si ea este concava crescatoare pe acest interval.
Dupa cum se stie, ca sa existe cel putin o solutie e necesar ca:\cdot f(B_{0})\leq 0)
Iata un desen:

Avem=\frac{f(B_{0})}{B_{1} B_ {0}}\Rightarrow B_{1}B_{0}=\frac{f(B_{0})}{f'(B_{0})})
Stim ca solutia noastra se afla spre stinga de punctul , solutia o notam cu
, solutia o notam cu  .
.
Scopul nostru e acesta: Sa calculam suma distantelor de la la
la 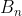 atunci cind
atunci cind  , si aici e ideea ca aceste distante fac parte din o functie care este asimptotica orizontala. Solutia noastra va fi:
, si aici e ideea ca aceste distante fac parte din o functie care este asimptotica orizontala. Solutia noastra va fi:
=B_{0}-\sum_{i=0}^{n\rightarrow \infty }B_{i+1}B_{i}=\lim_{n\rightarrow \infty }B_{n})
[Repet se poate si alt fel, depinde de cazuri si comoditate, spre exemplu determinind limita cind , la fel avem in cale o alta functie care si ea este o asimptota orizontala. determinarea limitei ei, determinam ca in cutarele punct
, la fel avem in cale o alta functie care si ea este o asimptota orizontala. determinarea limitei ei, determinam ca in cutarele punct =0) .
.
Se poate si asa o cale, nus' cit de avantajoasa si daca nu e a zecea roata: determinarea limitei in care punct aria triunghiurilor este egala cu
este egala cu  inseamna determinarea solutiei ecuatiei.]
inseamna determinarea solutiei ecuatiei.]
Memoram aceasta valoare a lui .
.
Adica}{f'(B_{0})}) , deci
, deci  .
.
Din=f'(B_{0}-B_{1}B_{0})=\frac{f(B_{0}-B_{1}B_{0})}{B_{2}B_{1}}) aflam ca:
aflam ca:}{f'(B_{1})}=\frac{f(B_{0}-B_{1}B_{0})}{f'(B_{0}-B_{1}B_{0})}=\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})})
Urmeaza aceeasi poveste:
}{f'(B_{0})}-\frac{f\left (B_{0}-\frac{fB_{0})}{f'(B_{0})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})} \right )})
Din relatia:=\frac{f(B_{2})}{B_{3}B_{2}}) aflam ca:
aflam ca: }{f'(B_{2})})
In termeni mai expliciti:
}{f'(B_{2})}=\frac{f(B_{0}-B_{1}B_{0}-B_{2}B_{1})}{f'(B_{0}-B_{1}B_{0}-B_{2}B_{1})}=\frac{f\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )})
Deci:
}{f'(B_{0})}-\frac{f\left (B_{0}-\frac{fB_{0})}{f'(B_{0})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})} \right )}- \frac{f\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )})
Apoi povestea se rea de la inceput si ajungem la aceea ca:

}{f'(B_{0})}-\frac{f\left (B_{0}-\frac{fB_{0})}{f'(B_{0})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})} \right )}-)
}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )} -)
}{f'(B_{0})}-\frac{f\left (B_{0}-\frac{fB_{0})}{f'(B_{0})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})} \right )}-\frac{f\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )} \right )}{f' \left( B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f\left (B_{0}-\frac{fB_{0})}{f'(B_{0})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})} \right )}-\frac{f\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )} \right )})
Pentru cazul general vom avea:
}{f'(B_{0})}-\frac{f\left (B_{0}-\frac{fB_{0})}{f'(B_{0})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})} \right )}- \frac{f\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )}-)
}{f'(B_{0})}-\frac{f\left (B_{0}-\frac{fB_{0})}{f'(B_{0})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})} \right )}-\frac{f\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )} \right )}{f' \left( B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f\left (B_{0}-\frac{fB_{0})}{f'(B_{0})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})} \right )}-\frac{f\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )}{f'\left (B_{0}-\frac{f(B_{0})}{f'(B_{0})}-\frac{f(B_{0}-\frac{f(B_{0})}{f'(B_{0})})}{f'(B_{0}-\frac{f(B_{0})}{f'(B_{0})})} \right )} \right )}-...)
Deci cine poate reduce aceste expresii in alt mod, sau a le calcula acea diferenta, aceala merita laude.
Aceasta nu e nimic nou si deosebit, ba mai mult posibil sa fie mai bine dezvoltat in ziua de az asa lucruri.
Insa o recapitulare pentru cine a uitat nu e rau.
Aceleasi povesti se petrec si la metoda coardelor, cu diferenta ca nu avem dea face cu derivate si nu sunt asa de compacte ( ).
).
Felul cum se aplica aceasta metoda, usor se poate face analogii catre alte metode, sa spunem catre metoda coardelor. Cel mai important e sa iasa la suprafata odata si odata o metoda finisata.
Deasemenea, de retinut ca fiecare metoda (mai ales in calculul numeric) are avantajele si dezavantajele ei [V.S. a avut o idee, cica: sa aplicam succesiv toate trei metode. Ideea e una buna, deoarece aduna la un loc in primul rind avantajele. In un numar mai mic de pasi, ne putem apropia (in dependenta de caz..) mai rapid de solutia ecuatiei, fata de alte metode particulare].
Fie este o functie continua si derivabila pe intervalul
Fie pentru cazul nostru functia o notam cu
Dupa cum se stie, ca sa existe cel putin o solutie e necesar ca:
Iata un desen:

Avem
Stim ca solutia noastra se afla spre stinga de punctul
Scopul nostru e acesta: Sa calculam suma distantelor de la
[Repet se poate si alt fel, depinde de cazuri si comoditate, spre exemplu determinind limita cind
Se poate si asa o cale, nus' cit de avantajoasa si daca nu e a zecea roata: determinarea limitei in care punct aria triunghiurilor
Memoram aceasta valoare a lui
Adica
Din
Urmeaza aceeasi poveste:
Din relatia:
In termeni mai expliciti:
Deci:
Apoi povestea se rea de la inceput si ajungem la aceea ca:
Pentru cazul general vom avea:
Deci cine poate reduce aceste expresii in alt mod, sau a le calcula acea diferenta, aceala merita laude.
Aceasta nu e nimic nou si deosebit, ba mai mult posibil sa fie mai bine dezvoltat in ziua de az asa lucruri.
Insa o recapitulare pentru cine a uitat nu e rau.
Aceleasi povesti se petrec si la metoda coardelor, cu diferenta ca nu avem dea face cu derivate si nu sunt asa de compacte (
Ultima editare efectuata de catre meteor in Dum 10 Feb 2013, 14:36, editata de 1 ori (Motiv : m-am clarificat cu formulele)
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25855
Data de inscriere : 19/06/2011
 Re: Calculul solutiilor ecuatiilor (deasemeni atentie speciala la ec. de grad mai mare ca 4)
Re: Calculul solutiilor ecuatiilor (deasemeni atentie speciala la ec. de grad mai mare ca 4)
Gasirea calcului solutiei ecuatiilor de grad mai mare ca 4, probabil s-a inpotmolit odata cu teorema ce spune ca calculul ecuatiilor de grad mai mare ca 4 nu se poat rezolva in radicali.
Stiinta, insa e stiinta, si sa stam cu capul in traista la asa ghind ca nu este iesiri, se pare ca e cel putin rusinos.
O idee interesanta mi-a venit:
- Sa descriem ecuatiile polinomiale de grad mai mare ca 4 (de dorit de inceput cu 5) in alte sisteme de coordonate, initial propun cu cel polar.
Apoi deasemeni de descris ecuatia abcisei (nu neaparat.. se poate o paralele de a ei, in asa caz insa si ecuatia polinomiala data va trebui trasata cu aceeasi distanta, aceasta nu e mare problema) care era in sistemul cartezian in sistemul dat.
Apoi de egalat cele 2 ecuatii, si de gasit necunoscuta.
Gasind cel putin o solutie noi, apoi o vom traduce in sistemul de coordonate cartezian, apoi usor putem cobori la un grad inferior ecuatia (aici deja vom avea din gradul 5 gradul 4, ceea ce e familiar. Dar daca putem aplica metoda la ecuatiile de gradul 5, trecem sa rezolvam ecuatiile de gradul 6, la care daca gasim cel putin o solutie, deasemeni o coborim la gradul 5 , care deja e familiar, etc.)
Ce vreau sa spun, caci in noul sistem cind descriem o ecuatie polinomiala, ea are cu totul alt aspect.
Aici avem de aface cu functii trigonometrice.
Ca sa ajungem la o variabile, spre epre exemplu putem face acele notatii: cosx= sqrt(1-sin^2 x); etc.
Aici posibil deja nu mai avem ecuatii cu grade mai mari ca gradul studiat.
In final ne ramine una doar, ca sa traducem solutia in sistemul de coordonate cartezian.
La fel se pot studia si calculul solutiilor altor ecuatii mai dificile, la care in cartezian se pare ca e foarte greu.
Mai dau un sfat mare, daca nici in polar nu se primeste nimic (pentru anumite ecuatii), se poate de lucrat cu sistemele de coordonate bicentral- biunghiular- segment.
Ce e straniu cu acest sistem este, ca valorile sunt niste unghiuri.
La fel a gasi solutia ecuatiei, inseamna a gasi o valoare a unui unghi.
Si aici deasemeni in final facem traducerea coordonatelor solutiei ecuatiei in sistemul cel mai familiar (cel de studiu).
La fel un sfat, se poate facilita de formula lui Euler, adica in final sa scriem deslusit cine este functia ceea trigonometrica, sa o scriem in un mod putin mai omenesc perceptibil.
Problema pe care o am la moment e caci cam ma ingreunez sa traduc in sistemul polar din cartezian, cum ar arata unele ecuatii.
Deasemeni, chiar tot in planul acesta bidimensional, banui ca se pot construi fel de fel de sisteme de coordonate, dupa placul si comoditatea noastra (adica de conditiile problemei..).
Stiinta, insa e stiinta, si sa stam cu capul in traista la asa ghind ca nu este iesiri, se pare ca e cel putin rusinos.
O idee interesanta mi-a venit:
- Sa descriem ecuatiile polinomiale de grad mai mare ca 4 (de dorit de inceput cu 5) in alte sisteme de coordonate, initial propun cu cel polar.
Apoi deasemeni de descris ecuatia abcisei (nu neaparat.. se poate o paralele de a ei, in asa caz insa si ecuatia polinomiala data va trebui trasata cu aceeasi distanta, aceasta nu e mare problema) care era in sistemul cartezian in sistemul dat.
Apoi de egalat cele 2 ecuatii, si de gasit necunoscuta.
Gasind cel putin o solutie noi, apoi o vom traduce in sistemul de coordonate cartezian, apoi usor putem cobori la un grad inferior ecuatia (aici deja vom avea din gradul 5 gradul 4, ceea ce e familiar. Dar daca putem aplica metoda la ecuatiile de gradul 5, trecem sa rezolvam ecuatiile de gradul 6, la care daca gasim cel putin o solutie, deasemeni o coborim la gradul 5 , care deja e familiar, etc.)
Ce vreau sa spun, caci in noul sistem cind descriem o ecuatie polinomiala, ea are cu totul alt aspect.
Aici avem de aface cu functii trigonometrice.
Ca sa ajungem la o variabile, spre epre exemplu putem face acele notatii: cosx= sqrt(1-sin^2 x); etc.
Aici posibil deja nu mai avem ecuatii cu grade mai mari ca gradul studiat.
In final ne ramine una doar, ca sa traducem solutia in sistemul de coordonate cartezian.
La fel se pot studia si calculul solutiilor altor ecuatii mai dificile, la care in cartezian se pare ca e foarte greu.
Mai dau un sfat mare, daca nici in polar nu se primeste nimic (pentru anumite ecuatii), se poate de lucrat cu sistemele de coordonate bicentral- biunghiular- segment.
Ce e straniu cu acest sistem este, ca valorile sunt niste unghiuri.
La fel a gasi solutia ecuatiei, inseamna a gasi o valoare a unui unghi.
Si aici deasemeni in final facem traducerea coordonatelor solutiei ecuatiei in sistemul cel mai familiar (cel de studiu).
La fel un sfat, se poate facilita de formula lui Euler, adica in final sa scriem deslusit cine este functia ceea trigonometrica, sa o scriem in un mod putin mai omenesc perceptibil.
Problema pe care o am la moment e caci cam ma ingreunez sa traduc in sistemul polar din cartezian, cum ar arata unele ecuatii.
Deasemeni, chiar tot in planul acesta bidimensional, banui ca se pot construi fel de fel de sisteme de coordonate, dupa placul si comoditatea noastra (adica de conditiile problemei..).
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25855
Data de inscriere : 19/06/2011
 Re: Calculul solutiilor ecuatiilor (deasemeni atentie speciala la ec. de grad mai mare ca 4)
Re: Calculul solutiilor ecuatiilor (deasemeni atentie speciala la ec. de grad mai mare ca 4)
[aceasta precuvintare apartine subiectului: Problema mileniilor]Ce importanta are in toata matematica si fizica teorema lui Pitagora ?!
Dupa parerea mea (repet), ACEEASI importanta atit in matematica chit si in fizica (eu personal cred caci chiar e mai important) o are formula lui Euler (ma refer concret ANUME la calculul functiilor trigonometrice din aceasta formula, ca de restul nu ma intereseaza nimic la moment).
Ce vreau sa zic e ca mai avem 2 sisteme de coordonate: polar si bicentral biunghiular.
Fie ca avem o anumita ecuatie la care nu ii putem gasi solutiile.
O posibila varianta de rezolvare e sa convertim functia in sistemul polar (sau bicentral biunghiular, dar mai rar caci e diochiat pe acolo).
Acolo in sistemul polar sa notam una din functiile trigonometrice cu o anumita necunoscuta, dupa care sa rezolvam propriu spus(daca e in putinta) noua ecuatie. Apoi din notatii sa determinam necunoscuta, si aici aplicam formula lui Euler, la care desigur cadem in numere imaginare, dar daca voi totii spuneti ca le-ati inteles, atunci e totul ok.
Dupa parerea mea (repet), ACEEASI importanta atit in matematica chit si in fizica (eu personal cred caci chiar e mai important) o are formula lui Euler (ma refer concret ANUME la calculul functiilor trigonometrice din aceasta formula, ca de restul nu ma intereseaza nimic la moment).
Ce vreau sa zic e ca mai avem 2 sisteme de coordonate: polar si bicentral biunghiular.
Fie ca avem o anumita ecuatie la care nu ii putem gasi solutiile.
O posibila varianta de rezolvare e sa convertim functia in sistemul polar (sau bicentral biunghiular, dar mai rar caci e diochiat pe acolo).
Acolo in sistemul polar sa notam una din functiile trigonometrice cu o anumita necunoscuta, dupa care sa rezolvam propriu spus(daca e in putinta) noua ecuatie. Apoi din notatii sa determinam necunoscuta, si aici aplicam formula lui Euler, la care desigur cadem in numere imaginare, dar daca voi totii spuneti ca le-ati inteles, atunci e totul ok.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25855
Data de inscriere : 19/06/2011
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 