Ultimele subiecte
» Impulsul elicoidalScris de virgil Joi 25 Iul 2024, 17:43
» New topic
Scris de virgil Mier 24 Iul 2024, 07:33
» Ce fel de popor suntem
Scris de CAdi Mar 23 Iul 2024, 22:12
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de CAdi Mar 23 Iul 2024, 06:47
» Fenomene Electromagnetice
Scris de eugen Lun 22 Iul 2024, 21:37
» Sa mai auzim si de bine in Romania :
Scris de virgil Lun 22 Iul 2024, 18:39
» Masina Timpului
Scris de CAdi Lun 22 Iul 2024, 13:17
» Globalizarea
Scris de virgil Dum 21 Iul 2024, 16:46
» Unde a ajuns stiinta ?
Scris de CAdi Dum 21 Iul 2024, 15:20
» Ce este FOIP?
Scris de Abel Cavaşi Vin 19 Iul 2024, 22:02
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de CAdi Joi 18 Iul 2024, 11:51
» Inertia
Scris de virgil Mier 17 Iul 2024, 11:09
» Lucrul mecanic - definitie si exemple (Secţiunea 2)
Scris de CAdi Mar 16 Iul 2024, 05:20
» Laborator-sa construim impreuna
Scris de eugen Lun 15 Iul 2024, 10:17
» Stanley A. Meyer - Hidrogen
Scris de eugen Dum 14 Iul 2024, 20:25
» Despre vise
Scris de CAdi Sam 13 Iul 2024, 15:09
» Constatari
Scris de curiosul Sam 13 Iul 2024, 10:13
» Pendulul
Scris de virgil_48 Lun 08 Iul 2024, 16:18
» Marea teorema a lui Fermat.
Scris de curiosul Sam 06 Iul 2024, 10:23
» Legi de conservare (2)
Scris de Vizitator Vin 05 Iul 2024, 13:24
» PROFILUL CERCETATORULUI...
Scris de virgil Dum 30 Iun 2024, 19:01
» Grup de cercetare pentru constiinta
Scris de curiosul Sam 29 Iun 2024, 16:06
» CURIOZITATI; Motor miniatural functional
Scris de virgil Vin 28 Iun 2024, 20:36
» Fizicieni care au schimbat lumea.
Scris de eugen Vin 28 Iun 2024, 09:58
» O proprietate Black Hole (Gaura Neagra)
Scris de virgil Joi 27 Iun 2024, 17:58
» Cum marim energia atomului ?
Scris de virgil Dum 23 Iun 2024, 19:11
» Bec Tapo L530E 2.0 - Smart Wi-Fi Light Bulb, Multicolor
Scris de Dacu Vin 21 Iun 2024, 18:30
» Caracteristicile tehnice ale motoarelor auto
Scris de CAdi Joi 20 Iun 2024, 12:24
» Concluzii asupra relativității
Scris de curiosul Dum 16 Iun 2024, 11:55
» EMINESCU, Templu National
Scris de eugen Sam 15 Iun 2024, 22:29
Postări cu cele mai multe reacții ale lunii
» Mesaj de la CAdi în TEORIA CONSPIRATIEI NU ESTE UN MIT... ( 2 )
» Mesaj de la CAdi în TEORIA CONSPIRATIEI NU ESTE UN MIT...
( 2 )
» Mesaj de la CAdi în TEORIA CONSPIRATIEI NU ESTE UN MIT...
( 2 )
» Mesaj de la eugen în Laborator-sa construim impreuna
( 2 )
» Mesaj de la eugen în Laborator-sa construim impreuna
( 2 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12347) | ||||
| CAdi (12205) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7950) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6162) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3889) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Spune şi altora
Cine este conectat?
În total sunt 50 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 50 Vizitatori :: 1 Motor de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Calculul integralelor
Pagina 1 din 1
 Calculul integralelor
Calculul integralelor
- E bine sa se elaboreze o metoda generala de calcul a integralelor, sa fie un algoritm, dupa care orice pusti sa il poata parcurge astfel rezolvind orice fel de integrala.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25489
Data de inscriere : 19/06/2011
 Re: Calculul integralelor
Re: Calculul integralelor
omuldinluna a scris:Atâta timp cât vorbim de integrale într-o singură dimensiune, există metode numerice care țin pentru orice, evident atâta timp cât integrala nu e divergentă. O metodă analitică cu adevărat universală nu cred să existe deoarece diverse funcții au diverse proprietăți: există metoda integrării prin părți sau a schimbării de variabilă, dar și metode specifice în cazul în care funcțiile de sub integrală sunt de diverse naturi. Există trecerea la variabilă complexă care permite integrarea unui număr foarte mare de integrale extrem de dificile dacă ne restrângem numai la mulțimea numerelor reale. În fine, există o întreagă teorie a analizei funcționale care permite dezvoltarea în serie a funcțiilor în tot soiul de baze (polinoame ortogonale, funcții hipergeometrice și alte minuni) care iarăși ține pentru o mulțime de funcții. Multe dintre acestea sunt aplicabile și la integrale multidimensionale, dar nu cred că poate exista o singură metodă, universal valabilă.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25489
Data de inscriere : 19/06/2011
 Re: Calculul integralelor
Re: Calculul integralelor
In primul rind, eu am ramas in epoca de piatra.. Nu studiez alte tipuri de integrale afara de cele cu o singura variabile, si alte ciudatenii de functii. Am aici prea multe incepute si mai nimic finisat.
Dar, cred caci deaici porneste totul. Daca am putea pe acestea sa le minuim bine, presupun ca vom putea si pe celelalte.
Is deacord, caci cam e sub semnul intrebarii, ca sa se gaseasca o metoda grozava care sa poata rezolva integralele din orice categorii.
Eu, nu prea convins 100%, dar voi arata ceva mai tirziu care e jmecheria cu care es la tirg. E foarte simplu si e mai mult sub forma de ipoteza.
Exsista insa o alta problema mai ca aceasta.. cu calculul unor integrale..
Dar, cred caci deaici porneste totul. Daca am putea pe acestea sa le minuim bine, presupun ca vom putea si pe celelalte.
Is deacord, caci cam e sub semnul intrebarii, ca sa se gaseasca o metoda grozava care sa poata rezolva integralele din orice categorii.
Eu, nu prea convins 100%, dar voi arata ceva mai tirziu care e jmecheria cu care es la tirg. E foarte simplu si e mai mult sub forma de ipoteza.
Exsista insa o alta problema mai ca aceasta.. cu calculul unor integrale..
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25489
Data de inscriere : 19/06/2011
 Re: Calculul integralelor
Re: Calculul integralelor
Iata care e toata pacaleala:
dx & f(x) & f^{'}(x) & f^{''}(x) & ... & f^{(n)}(x) \end{matrix}) .
.
Ai functia) . Determini daca e derivabila.
. Determini daca e derivabila.
[Se stie bine ca derivarea a foarte multor functii nu este o problema, acest avantaj se considera ca fiind prima chee]
Ii gasesti prima derivata. Apoi a doua derivata, etc. derivata de ordinul n.
Urmaresti faptul cum functia cu derivata inferioara se modifica la derivata superioara. Observind acesta evolutie , si fiind prof in toate astea, cred ca se poate de mers inapoi.. adica sa ajungem sa aflam care este integrala cutarei functii.
Fiind mai capos, cred ca s-ar putea gasi integrala de ordinul n, din o singura lovitura, aceasta deja este ceva, insa .. pina atunci presupun ca mai este..
Spre exemplu se stie derivatele de ordinul n din o multime de functii elementare si compuse.
Mai avem (usor se deduce) formula lui Leibniz de calcul a derivatelor de orinul n din o functie care este egala cu produsul a doua functii:
}(x)=(g(x)h(x))^{n}=\sum_{i=0}^{n}C_{n}^{i}g^{(n-i)}(x)h^{(i)}(x))
La fel se pot elabora formule pentru cazurile cind functia reprezinta impartierea dintre 2 functii, o functie ridicata la puterea altei functii, etc. [de remarcat, ca aproape in toate cazurile apare factorialul, fie sub forma de combinari, fie sub alte forme]
Stiind toate acestea, posibil sa se usureze calculul integralei
Ai functia
[Se stie bine ca derivarea a foarte multor functii nu este o problema, acest avantaj se considera ca fiind prima chee]
Ii gasesti prima derivata. Apoi a doua derivata, etc. derivata de ordinul n.
Urmaresti faptul cum functia cu derivata inferioara se modifica la derivata superioara. Observind acesta evolutie , si fiind prof in toate astea, cred ca se poate de mers inapoi.. adica sa ajungem sa aflam care este integrala cutarei functii.
Fiind mai capos, cred ca s-ar putea gasi integrala de ordinul n, din o singura lovitura, aceasta deja este ceva, insa .. pina atunci presupun ca mai este..
Spre exemplu se stie derivatele de ordinul n din o multime de functii elementare si compuse.
Mai avem (usor se deduce) formula lui Leibniz de calcul a derivatelor de orinul n din o functie care este egala cu produsul a doua functii:
La fel se pot elabora formule pentru cazurile cind functia reprezinta impartierea dintre 2 functii, o functie ridicata la puterea altei functii, etc. [de remarcat, ca aproape in toate cazurile apare factorialul, fie sub forma de combinari, fie sub alte forme]
Stiind toate acestea, posibil sa se usureze calculul integralei
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25489
Data de inscriere : 19/06/2011
 Re: Calculul integralelor
Re: Calculul integralelor
Deci sa incerc a dezvolta incetul ideea (va trebui sa scriu mesaje multe, ca din cauze timpului scirt de editare nu pot sa scriu pe bucatele).
[Vorbesc de integrale in real cu o singura variabila, despre functii dea alea normale, nu de alea cine stie cu ce nazbitii, iesite din domeniul de definitie a teoriei (asa exemplu poate e functile Akerman)]
Stim ca daca o functie e derivabila, atunci ea admite si integrala.
Derivata functiei se stie azi, in mare parte, cum se face, deci i se poate gasi si derivata de un ordin oarecare n}(x)) .
.
Derivata integralei (primitivei) trebue sa ne dea insusi functia care e integrata.
Vom numi derivata de ordenul 0 insusi functia care o avem in fata, initiala}(x)=f(x)) .
.
La fel:}(x)=\int&space;\left&space;(&space;f^{(-k+1)}(x)&space;\right&space;)dx=F^{(k)}+c_{k}x^{k-1}+c_{k-1}x^{k-2}+...+c_{1})
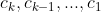 sunt anumite constante...
sunt anumite constante...
Ca sa nu ne ducem la integrale de orden superior, unde posibil sa ne manince curcile, mai bine raminem la indegrala de ordenul 1, sau derivata de odenul -1.
Ideea deci asa ramine: Stiind derivata de ordenul n, inlocuind -1 in expresie vom determina integrala.
De remarcat ca mergind mai departe, de ce sa nu fie si derivate fractionare (neintregi) ?! Nu stiu daca are vreun sens, si daca are sens unde anume se aplica.
Sa luam sa analizam chite un exemplu de functii.
^{(n)}=\frac{\lambda&space;!}{(\lambda&space;-n)!}x^{\lambda&space;-n})
}(x)=(g(x)h(x))^{n}=\sum_{i=0}^{n}C_{n}^{i}g^{(n-i)}(x)h^{(i)}(x))
^{(n)}=&space;a^{x}ln(a)+a^{x-1}+(x-1)(x-2)a^{x-2}+..+\frac{(x-1)!}{(x-n)!}a^{x-n+1})
(Dupa prima deriva vedem ca avem produsul a doua functii, deci derivata de ordenul n-1 o vom afla prin metoda de mai sus)
[vedem ca in foarte multe cazuri apare factorialul, si mai vedem ca per derivate neintregi cu functia gama poate va merge lucrurile, insa per valori negative nu pre, mai ramine de studiat]
[Vorbesc de integrale in real cu o singura variabila, despre functii dea alea normale, nu de alea cine stie cu ce nazbitii, iesite din domeniul de definitie a teoriei (asa exemplu poate e functile Akerman)]
Stim ca daca o functie e derivabila, atunci ea admite si integrala.
Derivata functiei se stie azi, in mare parte, cum se face, deci i se poate gasi si derivata de un ordin oarecare n
Derivata integralei (primitivei) trebue sa ne dea insusi functia care e integrata.
Vom numi derivata de ordenul 0 insusi functia care o avem in fata, initiala
La fel:
Ca sa nu ne ducem la integrale de orden superior, unde posibil sa ne manince curcile, mai bine raminem la indegrala de ordenul 1, sau derivata de odenul -1.
Ideea deci asa ramine: Stiind derivata de ordenul n, inlocuind -1 in expresie vom determina integrala.
De remarcat ca mergind mai departe, de ce sa nu fie si derivate fractionare (neintregi) ?! Nu stiu daca are vreun sens, si daca are sens unde anume se aplica.
Sa luam sa analizam chite un exemplu de functii.
(Dupa prima deriva vedem ca avem produsul a doua functii, deci derivata de ordenul n-1 o vom afla prin metoda de mai sus)
[vedem ca in foarte multe cazuri apare factorialul, si mai vedem ca per derivate neintregi cu functia gama poate va merge lucrurile, insa per valori negative nu pre, mai ramine de studiat]
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25489
Data de inscriere : 19/06/2011
 Subiecte similare
Subiecte similare» Calculul solutiilor ecuatiilor (deasemeni atentie speciala la ec. de grad mai mare ca 4)
» Calculul aproximativ al sumelor
» Calculul inversei unei functii si aplicatii ale acestei inversatii
» Calculul aproximativ al sumelor
» Calculul inversei unei functii si aplicatii ale acestei inversatii
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum|
|
|




 Devino fan Forumgratuit
Devino fan Forumgratuit 