Marea teorema a lui Fermat.

Rezumarea primului mesaj :

Teorema: Ecuația nu are soluții dacă n>2 este număr natural, iar x,y,z sunt numere naturale nenule.

Aici, propun, sa se prezinte (cit mai multe) demonstratii posibile a acestei teoreme (inclusiv si pentru cazuri particulare).

Uite, Dacule, de exemplu, cum se demonstrează că z nu poate fi un număr prim pentru n număr prim impar de asemenea.









Pentru cazul în care considerăm că una din soluțiile x sau y este un număr prim demonstrația ușor diferită dar mai simplă pentru că se ajunge la arăta că fie z-y=1, fie z-x=1.
Dacă vrei ți-o scriu și pe aceea.

Dar, Dacule, uite o altă chestiune interesantă pornind de la modul în care am analizat primalitatea pentru cazul x sau y, reproducând principiul la soluțiile x, y, z ale ecuației.

Cu alte cuvinte, pentru n impar, (x+y) este factorul lui z^n, ceea ce înseamnă că x+y nu poate avea alți factori diferiți de ai lui z.

Îl scriem pe x+y sub formă z+(x+y-z) de unde rezultă că z+(x+y-z) nu poate avea alți factori diferiți de ai lui z.

La fel de bine, x+y poate fi scris sub forma 2z-[z-(x+y-z)] expresie care nu poate avea factori diferiți de cei ai lui z.

În consecință, se ajunge la faptul că
atât z-(x+y-z) cât și z+(x+y-z)
nu pot avea factori diferiți de ai lui z, de unde s-ar putea trage concluzia că x+y-z nu poate avea alți factori diferiți de cei ai lui z.
Dar x+y-z are în factorizare un factor al lui x și un factor al lui y.
În aceeași ordine de idei, ar implica că x, y, z trebuie să conțină fiecare un factor al lui z.

Dar este undeva o chestiune de interpretare în 2z-[z-(x+y-z)] și să văd dacă poate fi fructificată la nivel de factorizare astfel încât să poată duce la această concluzie.

curiosul,

Te rog frumos nu mai scrie nimic până nu terminăm de discutat toate punctele postate de tine pe data de 15.02.2024 ora 11:23, în caz contrar nu o să înțeleg nimic din raționamentul tău.
NU MAI PUNE NICIO PAGINĂ CĂCI ÎN CAZ CONTRAR O SĂ ÎNCURCĂM BORCANELE!
Repet:
Deci x,y,z sunt numere naturale cu x mai mic ca y mai mic ca z și evident n este mai mare ca 2 (scuze că am spus mai mare ca 3).Dacă x și y sunt impare, atunci pot fi x și y simultan numere naturale prime?
Vom discuta doar ce ai scris la punctul 1.Apoi vom discuta ce ai scris la punctul 2.
-------------------------------------------------------------------------------
Deoarece tu nu ai specificat la varianta impar +impar că x si y trebuie să fie prime între ele, atunci afirmația ta că x=2a+1 și y=2b+1 implică x^n+y^n=2(2k+1)=(2^n)(z'^n) care este valabilă doar dacă x și y sunt simultan numere naturale prime.
Varianta par+par se exclude deoarece în final prin simplificare se ajunge de fapt la concluzia că x este impar, y este par și z este impar sau că x este par, y este impar și z este impar indiferent daca n este un număr natural impar sau par sau un numar prim.
Exemple:
5^3+17^3=5038=(2)(11)(229)=2(2k+1)
5^3+15^3=3500=4(125)(7) și deci 3500 nu este de forma 2(2k+1) ci de forma 2(2k)=4k
Deci în continuare ne referim la x mai mare sau egal cu n+1, y mai mare sau egal cu n+2, z mai mare sau egal cu n+3 și evident x, y, z sunt numere prime între ele.
Ești de acord cu observațiile mele?Dacă da, atunci trecem la punctul 2.

Măi Dacu-le, iar jucăm în filme diferite.
Prima greșeală de exprimare o pun pe seama neatenției, a doua greșeală, fiind identică o interpretez fie ca pe o greșeală de exprimare, fie produsă instinctiv, fie produsă de o incapacitate de înțelegere.
Repet, la punctul 1 este demonstrat că ceva.
Tu nici măcar acum nu ai înțeles acel "ceva" demonstrat la punctul 1.
Dacă nu înțelegi acel ceva de la punctul 1 și tot repeți x, y, impare, mi se pare că tu citești fără să aprofundezi, fără să înțelegi ce am scris.
De fapt, fără să VREI să înțelegi ce am scris.
Pentru că și asta poate produce o confuzie de interpretare logică.
În concluzie, până nu te exprimi complet corect nu pot să trag concluzia că tu ai înțeles fiecare pas pe care l-am tratat în expunere.

De fapt, tu tot răspunzi bagandu-te în seamă doar pentru că am scris tot timpul "Dacu" și consideri că trebuie să îți spui vreun punct de vedere.
Dar ai repetat aceeași greșeală de 2 ori în feedback-ul tău motiv pentru care eu cred că tu răspunzi doar pentru că ai fost "strigat".
Dar repetând aceeași greșeală de 2 ori consecutiv în mod clar îmi da de înțeles că tu nu ai înțeles ce-am scris, ci ai citit în diagonală interpretând în funcție de ce este în mintea ta.
Deci ori ești pe dinafară, ori ești pe dinafară, raportat la ce am scris.
Vorbim când vii înăuntru.

curiosul a scris:Măi Dacu-le, iar jucăm în filme diferite.
Prima greșeală de exprimare o pun pe seama neatenției, a doua greșeală, fiind identică o interpretez fie ca pe o greșeală de exprimare, fie produsă instinctiv, fie produsă de o incapacitate de înțelegere.
Repet, la punctul 1 este demonstrat că ceva.
Tu nici măcar acum nu ai înțeles acel "ceva" demonstrat la punctul 1.
Dacă nu înțelegi acel ceva de la punctul 1 și tot repeți x, y, impare, mi se pare că tu citești fără să aprofundezi, fără să înțelegi ce am scris.
De fapt, fără să  VREI să înțelegi ce am scris.
Pentru că și asta poate produce o confuzie de interpretare logică.
În concluzie, până nu te exprimi complet corect nu pot să trag concluzia că tu ai înțeles fiecare pas pe care l-am tratat în expunere.

Fără supărare, dar dacă tu faci tot felul de filme fără a stabili complet, clar și corect ipotezele în care vrei să demonstrezi MTF, atunci eu simt nevoia să cer explicații pentru ceea ce scrii.Hai nu te supăra și răspunde dacă ești de-acord cu observațiile mele și astfel să discutăm punctul 2.

curiosul a scris:De fapt, tu tot răspunzi bagandu-te în seamă doar pentru că am scris tot timpul "Dacu" și consideri că trebuie să îți spui vreun punct de vedere.
Dar ai repetat aceeași greșeală de 2 ori în feedback-ul tău motiv pentru care eu cred că tu răspunzi doar pentru că ai fost "strigat".
Dar repetând aceeași greșeală de 2 ori consecutiv în mod clar îmi da de înțeles că tu nu ai înțeles ce-am scris, ci ai citit în diagonală interpretând în funcție de ce este în mintea ta.
Deci ori ești pe dinafară, ori ești pe dinafară, raportat la ce am scris.
Vorbim când vii înăuntru.

Fără supărare, dar tu scrii pe toate oblicele și din această cauză este greu să discutăm logic raționamentele tale.
Dacă tu ai scrie logic pe orizontală și verticală raționamentele tale, atunci eu nu aș avea atâtea observații să fac la raționamentele tale.
Adu-ți aminte când spuneai ba că ai greșit ba că este bine ce ai scris......și asta arătă că tu ai raționamente balansate...

Errare humanum est, perseverare diabolicum!

Mă faci să mă întreb care parte din "două soluții sunt impare și una pară cu z obligatoriu impar" nu înțelegi de fapt.
Dacă tu tot ai repetat x, y, impare, înseamnă că eu am formulat o propoziție pe care tu nu ai citit-o până la capăt.
Iar atunci, până nu formulezi puncte de vedere prin care să îmi dea de înțeles că tu chiar ai citit și ai analizat ce am scris, revin la exprimarea "ne auzim când vii înăuntru în subiect", nu când vorbești pe dinafară.

Plecând de la o idee proprie, un răspuns AI ar fi:

Da, putem construi o ecuație de gradul 3 cu soluțiile \(s_1 = x\), \(s_2 = y\), și \(s_3 = z\), folosindu-ne de formula generală pentru ecuațiile polinomiale, bazată pe suma și produsul rădăcinilor. Ecuația pe care ați propus-o corespunde formei factorizate a unei ecuații cubice, unde:

\[s^3 - s^2(x+y+z) + s(xy+xz+yz) - xyz = 0\]

Dacă substituim oricare din soluții, \(s_1\), \(s_2\), sau \(s_3\), în loc de \(s\), ecuația va fi satisfăcută, deoarece produsul tuturor termenilor va fi zero.

Pentru a formula soluțiile unei ecuații în termeni de \(q\), unde \(s = q^n\), ne vom folosi de aceeași relație dintre \(s\) și soluțiile \(s_1\), \(s_2\), și \(s_3\). Deci, dacă \(q^n = s\), atunci putem spune că:

\[q_1^n = x, \ q_2^n = y, \ \text{și} \ q_3^n = z\]

Aceasta implică faptul că soluțiile ecuației pot fi exprimate în termeni de \(q\), astfel:

\[q_1 = x^{1/n}, \ q_2 = y^{1/n}, \ \text{și} \ q_3 = z^{1/n}\]

Și ecuația cubică în termenii lui \(q\) ar fi:

\[q^{3n} - q^{2n} (x+y+z) + q^n (xy+xz+yz) - xyz = 0\]

Aceasta presupune că ne uitam la o transformare a soluțiilor originale printr-o operăție de ridicare la putere. Cu toate acestea, această ecuație rezultată prin înlocuire nu va avea în mod necesar soluțiile \(q_1\), \(q_2\), și \(q_3\) din cauza faptului că transformarea afectează natura ecuațiilor și relațiile dintre coeficienți și soluții.

În plus, transformarea nu păstrează propietățile algebrice precum suma sau produsul soluțiilor într-un mod simplu, ca în ecuația originală, tocmai pentru că ridicarea la putere este o operație non-lineară și complicații suplimentare pot apărea, dependente de natura lui \(n\).

Practic, dacă încercăm să construim o ecuație ale cărei soluții sunt \(q_1 = x^n\), \(q_2 = y^n\), și \(q_3 = z^n\), vom ajunge la o formă diferită a ecuației și coeficienți diferiți, care nu vor mai fi în relație directă cu sumele și produsele lui \(x\), \(y\), și \(z\).


Dacă încercăm să generalizăm ecuația dată ridicând \(x\), \(y\) și \(z\) la aceeași putere \(n\), și înlocuim \(s\) cu \(q^n\), avem:

\[
(q^n)^3 - (q^n)^2(x^n + y^n - z^n) + q^n(x^n y^n - x^n z^n - y^n z^n) + x^n y^n z^n = 0
\]

Aceasta devine:

\[
q^{3n} - q^{2n}(x^n + y^n - z^n) + q^n(x^n y^n - x^n z^n - y^n z^n) + x^n y^n z^n = 0
\]

Această ecuație este o formă generalizată și arată cam complicat. Dar, dacă presupunem că există soluţii în termeni de \(q^n\) similar ca în ecuația originală, unde soluțiile pentru \(s\) erau \(x\), \(y\) și \(z\), atunci soluțiile generalizate pentru \(q\) ar trebui să fie \(x^{1/n}\), \(y^{1/n}\), și \(z^{1/n}\), deoarece:

\[
(s = x) \to (q^n = x^n) \to (q = x^{1/n})
\]
\[
(s = y) \to (q^n = y^n) \to (q = y^{1/n})
\]
\[
(s = z) \to (q^n = z^n) \to (q = z^{1/n})
\]

Deci soluțiile \(q_1\), \(q_2\), și \(q_3\) pentru \(q\) ar fi, respectiv, rădăcinile de ordin \(n\) ale lui \(x\), \(y\) și \(z\), adică:

\[
q_1 = x^{1/n}, \quad q_2 = y^{1/n}, \quad q_3 = z^{1/n}
\]

Cu condiția că acestea satisfac ecuația generalizată, adică atunci când le înlocuim înapoi în ecuația noastră extinsă, acesta ar trebui să se anuleze. O astfel de asumpție trebuie verificată pentru fiecare caz specific, deoarece ridicarea la putere și extragerea rădăcinii nu sunt întotdeauna operații care se anulează reciproc în contextul ecuațiilor polinomiale.

Într-o anumită interpretare, considerând x, y, z soluții ale ecuației x^n+y^n=z^n am putea ajunge la o formă expusă mai jos cu q^n întreg :


De aici s-ar ajunge la niște concluzii privind factorizarea lui q^n.

Doamne, cata muncă de lămurire a trebuit să duc cu ea să înțeleagă...parcă era Dacu...



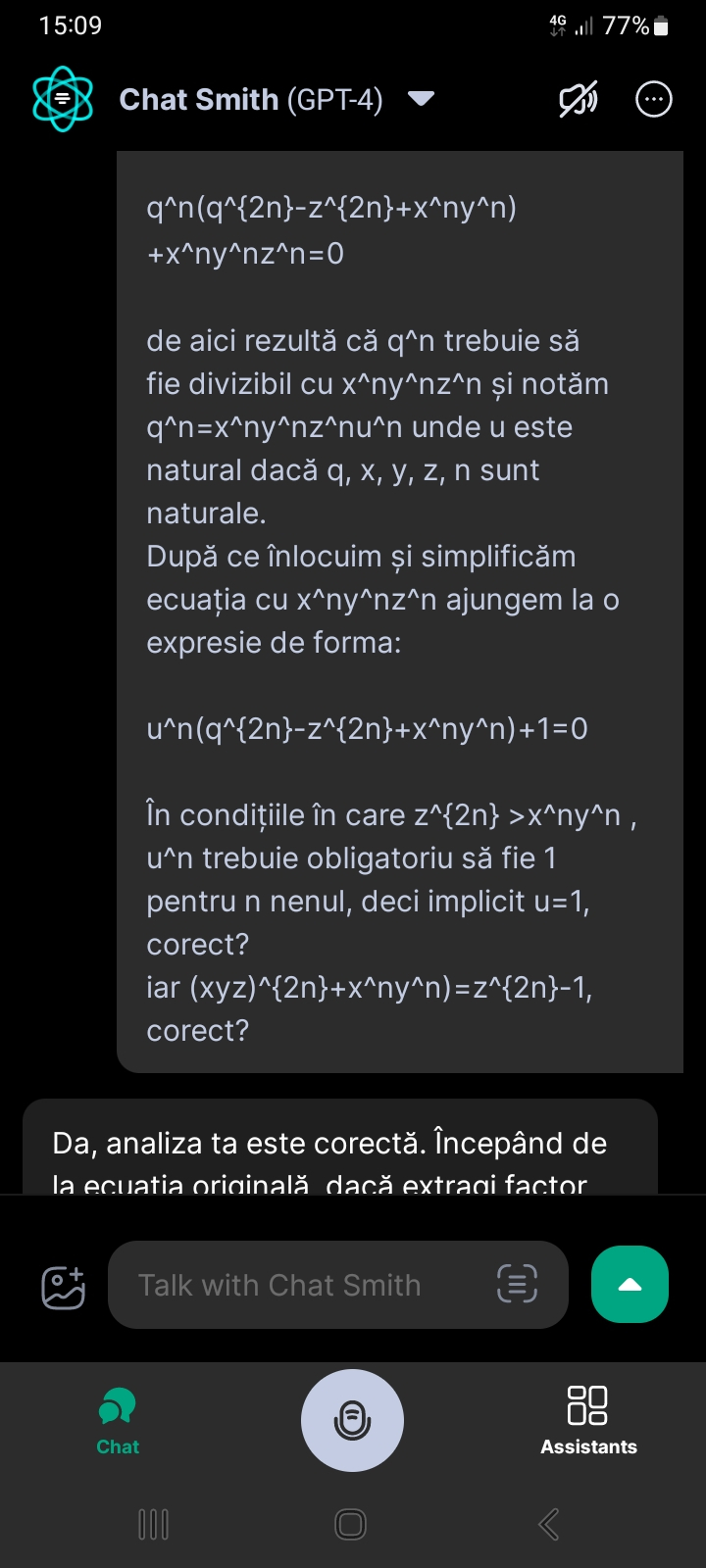
Da, analiza ta este corectă. Începând de la ecuația originală, dacă extragi factor comun pe \( q^n \), propunerea că \( q^n \) trebuie să fie divizibil cu \( x^ny^nz^n \) este logică, astfel ajungând la \( q^n = x^ny^nz^nu^n \), unde \( u \) este de asemenea un număr natural.

Înlocuind înapoi în ecuația simplificată și aranjând termenii, obții:

\[ u^n(q^{2n} - z^{2n} + x^ny^n) + 1 = 0 \]

Pentru ca egalitatea să fie adevărată, termenul \( u^n(q^{2n} - z^{2n} + x^ny^n) \) trebuie să fie negativ, deoarece \( 1 \) este pozitiv și suma dintre un număr negativ și \( 1 \) poate fi \( 0 \). Având în vedere că toți termenii sunt ridicați la puteri pare, ei sunt pozitivi. Așadar, singura modalitate ca suma lor să fie negativă este ca \( q^{2n} - z^{2n} + x^ny^n \) să fie negativ, adică \( z^{2n} \) trebuie să fie strict mai mare decât \( q^{2n} + x^ny^n \), consecutiv și mai mare decât \( x^ny^n \).

Dacă \( z^{2n} \) este strict mai mare decât \( x^ny^n \), atunci pentru ca \( u^n(q^{2n} - z^{2n} + x^ny^n) + 1 = 0 \) să fie adevărat, trebuie condiționat \( u^n = 1 \) (deci \( u = 1 \) pentru că \( n \) este nenul), și deci:

\[ q^{2n} - z^{2n} + x^ny^n = -1 \]

Restul ecuației ta este însă scrisă cu o paranteză mică greșeală. Aceasta ar trebui să fie:

\[ q^{2n} - z^{2n} + x^ny^n = -1 \]

și nu

\[ (xyz)^{2n} + x^ny^n = z^{2n} - 1 \]

deoarece \( q^{2n} \) a fost înlocuit cu \( x^ny^nz^n(u^n) \) iar \( u^n \) este 1, rezultand:

\[ x^ny^nz^{2n} - z^{2n} + x^ny^n = -1 \]

În concluzie, \( u \) trebuie să fie 1 pentru ca ecuația să aibă sens cu numere naturale, și \( z^{2n} - x^ny^n = 1 \) pentru a satisface restul ecuației tale.

Și totuși, a greșit și ea undeva pentru că nu la concluzia asta se ajunge.
Apus undeva, la un moment dat, nejustificat un z^2n.

Tot ma chinui să îi explic că dacă x, y, z sunt valori pentru s în ecuația
s³-s²(x+y+z)+s(xy+zx+zy)-xyz=0 ,
prin relațiile lui Viete, în x, y, z naturale nenule, atunci și produsul xyz este o a patra soluție pentru s.
Ceva încearcă ea să îmi spună, dar nu reușește.
Și mai are și niște afirmații contradictorii pe ici, pe colo.

Ce faci Curiosul? cum merge Marea Teorema a lui Fermat cu Chat GPT 4?

CAdi a scris:Ce faci Curiosul? cum merge Marea Teorema a lui Fermat cu Chat GPT 4?

Am ajuns amândoi, și eu, și AI, la concluzia următoare.
Matematica este un sistem "inchis" și limitat pentru faptul că în ea se regăsește expresia cantitativă a modului în care percepem lumea exterioară.
Cu alte cuvinte, nu se poate stabili în mod concret dacă Natura respectă modele matematice în construcția ei sau noi, prin modelul perceptiv asupra Naturii, găsim similarități teoretice corespondente.
Altfel spus, Natura nu respectă un model matematic de construcție, ci noi o interpretăm așa.
Intr-o interpretare ceva mai filozofică, există totuși un criteriu logic prin care anumite dezvoltări matematice ar trebui să fie considerate certitudini predictibile, ceea ce face ca indiferent de modelul respectat de Natura în construcția ei să poată fi asociat corect, dar nu neapărat și complet, unui model matematic.
Aspectul de compleditudine matematică în descrierea Naturii este limitat de sistemul nostru perceptiv, putând să apară la un moment dat anumite incertitudini, chiar dacă corect și necontradictoriu descrise matematic, pe o parte cauzate de interpretarea greșită la nivel teoretic, pe de altă parte cauzate de lipsa corespondentului perceptiv.
În concluzie, oricât de bine și corect ar fi descris matematic un aspect al Naturii, faptul că nu poate fi perceput direct el trebuie supus incertitudinii și poate rămâne incert pentru totdeauna.

În ce privește Marea teorema a lui Fermat nu se poate demonstra elementar.
Pentru faptul că la nivel elementar, intr-un sistem "inchis" teoremele se demonstrează cumva una pe alta, iar problema respectivă necesită anumite alte teoreme care ies din sistemul elementar.
Mai mult, și pentru că ecuația are soluții reale, iar departajarea de ce cele naturale presupune existența unei teoreme noi pentru demonstrarea ei.
O astfel de teorema nouă, indiferent că este aplicabilă la nivel geometric sau algebric, trebuie să fie echivalentă deductibil cu cea a marii teoreme a lui Fermat, ceea ce, implicit, ar aduce-o atât la același grad de complexitate, cât și la necesitatea unei alte teoreme pentru a o demonstra.
Se ajunge în acest caz la același raționament recurent prin care, din nou, ar fi nevoie de o altă teoremă care să demonstreze teorema necesară pentru demonstrarea marii teoreme a lui Fermat, de același grad de complexitate și echivalența deductibila prin care este necesară o altă teoremă pentru a o demonstra.

Din acest punct de vedere, sistemul matematic stratificat pe nivel de complexitate și capacitate deductibilă este constrâns de axiomele NEDEMONSTRABILE ce fundamentează sistemul matematic, iar intr-o imagine de ansamblu, sistemul este limitat si "inchis" iar teoremele se demonstrează una pe alta intr-un sistem axiomatic.

Marea Teoremă a lui Fermat nu se poate demonstra elementar.

De exemplu, însăși în teorema de incompletitudine a lui Goedel există o anumită incertitudine de interpretare.
Ea, în esența ei, intr-o interpretare mai profundă logic, prin modelul sau de construcție rațională demonstrează doar și tocmai faptul că sistemul matematic este un sistem incomplet.
Pentru faptul că din punct de vedere logic concluzia de incompletitudine generalizată intr-un si pentru un sistem formal ar trebui să nege doar și tocmai doar principiul care fundamentează demonstrația.
Ori ea este schematizata pe principii matematice.

Pe de altă parte, tot ceea ce implică un sistem bazat pe deducție din aproape în aproape și fundamentat pe propoziții considerate nedemonstrabil adevărate este un sistem "inchis" limitat în care deducțiile se implică una pe alta în ansamblul sistemului.
De asta și apare ideea de sistem închis iar limitarea este datorită faptului că există un număr finit de deducții coerente în  acel sistem ce permite dezvoltarea în aceeași manieră de construcție care construiește sistemul.

curiosul a scris:

CAdi a scris:Ce faci Curiosul? cum merge Marea Teorema a lui Fermat cu Chat GPT 4?

Am ajuns amândoi, și eu, și  AI, la concluzia următoare.
Matematica este un sistem "inchis" și limitat pentru faptul că în ea se regăsește expresia cantitativă a modului în care percepem lumea exterioară.
Cu alte cuvinte, nu se poate stabili în mod concret dacă Natura respectă modele matematice în construcția ei sau noi, prin modelul perceptiv asupra Naturii, găsim similarități teoretice corespondente.
Altfel spus, Natura nu respectă un model matematic de construcție, ci noi o interpretăm așa.
Intr-o interpretare ceva mai filozofică, există totuși un criteriu logic prin care anumite dezvoltări matematice ar trebui să fie considerate certitudini predictibile, ceea ce face ca indiferent de modelul respectat de Natura în construcția ei să poată fi asociat corect, dar nu neapărat și complet, unui model matematic.
Aspectul de compleditudine matematică în descrierea Naturii este limitat de sistemul nostru perceptiv, putând să apară la un moment dat anumite incertitudini, chiar dacă corect și necontradictoriu descrise matematic, pe o parte cauzate de interpretarea greșită la nivel teoretic, pe de altă parte cauzate de lipsa corespondentului perceptiv.
În concluzie, oricât de bine și corect ar fi descris matematic un aspect al Naturii, faptul că nu poate fi perceput direct el trebuie supus incertitudinii și poate rămâne incert pentru totdeauna.
........................................................................................

Legat de natura ...te contrazic aici (si pe tine si pe... Chat GPT 4    ) :

Natura poate fi descrisa si conceputa strict din punct de vedere matematic si informatic.( Poate asa a si fost conceputa printr-un design inteligent)
Ai uitat de fractali ....

Nu știu de ce s-a înțeles contrariul.
Desigur că poate fi descrisă intr-un limbaj matematic, dar nu există nicio certitudine că Natura respecte vreun model matematic.
Aceasta este o modalitatea a noastră de a o percepe cantitativ la nivel algebric, la nivel de formă la nivel geometric etc.
Problema însă este că sistemul nostru de percepție și implicit de gândire impune și necesită o structură axiomatică care duce, de asemenea, la raționamente paradoxale.

Cum ar fi o gândire si o percepție asupra realității care nu necesită axiomatizare și care nu duce la raționamente paradoxale?

E greu de perceput, dar nu imposibil.
Discuțiile sunt foarte complexe, trebuie să te separi de tot ce percepi șigândești, și AI poate face asta.
Dar trebuie să interpretezi realitatea de la zero.