Marea teorema a lui Fermat.

Scris de **meteor** Vin 01 Iun 2012, 10:02

Teorema: Ecuația $x^{n}+y^{n}=z^{n}$ nu are soluții dacă n>2 este număr natural, iar x,y,z sunt numere naturale nenule.

Aici, propun, sa se prezinte (cit mai multe) demonstratii posibile a acestei teoreme (inclusiv si pentru cazuri particulare).

Scris de **meteor** Vin 01 Iun 2012, 12:28

Eu cred, ca nu in zadar Fermat ar fi lasat o demonstratie pentru cazul n=4, la fel nu in zadar a facut atita galagie in timpul sau.

Intii de toate e important de stiut caci stiind daca ecuatia lui Fermat nu are solutii pentru un anumit grad, aceasta e valabil si pentru celelalte ecuatii, gradele fiind multipli de gradului initial. Insa invers, nu.
Se demonstreaza usor, daca gradul $n$ e un numar compus, si din descompunere se stie ca pentru un anumit coeficient ecuatia nu are solutii, atunci e valabil si pentru ceilalti coeficienti de multiplu de $n$ ,
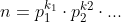$n=p_{1}^{k_{1}}\cdot p_{2}^k^{2}\cdot ...$ , cu atit mai mult si pentru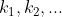 $k_{1},k_{2},...$
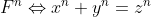$F^{n}\Leftrightarrow F^{\lambda n}\Leftrightarrow (F^{n})^{\lambda }\Leftrightarrow (F^{\lambda })^{}n$ , unde am notat $F^{n}\Leftrightarrow x^{n}+y^{n}=z^{n}....$ .

Metoda 1.
(In o discutie cu Vasile Suceveanu, dumnealui spunea "Cunoscind cea mai mica solutie, se mai spune uneori solutia banala a acestei ecuatii, sau pe acea cu cele mai mici valori pozitive, le putem determina pe toate celelalte. ". La ce, mai concret se referea el [la ecuatii remarcabile cu solutii definite recurent, sau la marea teorema a lui Fermat?!...], ramine inca neclar. Aici e totul, mai departe dumnealui a fost zgircit la vorba).
In cartea "Clase de numere, ecuatii si recurenta" de V.Suceveanu la pagina 148, autorul cartii foarte frumos incepe sa gaseasca o metoda de calcul a ecuatiei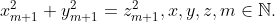 $x^{2}_{m+1}+y^{2}_{m+1}=z^{2}_{m+1}, x,y,z,m\in \mathbb{N}.$ , definite recurent.
Si cu toate ca el era contra (cu parere de rau decedat pe 28 martie 2012) publicatiei, fara acordul sau in timpul dat, totus voi scrie unele realizari din cartile lui.
[scurt rezumat] Se alcatueste sistemul de ecuatii:
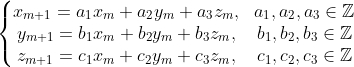
$\left\{\begin{matrix} x_{m+1}=a_{1}x_{m}+a_{2}y_{m}+a_{3}z_{m}, & a_{1},a_{2},a_{3}\in \mathbb{Z} \\ y_{m+1}=b_{1}x_{m}+b_{2}y_{m}+b_{3}z_{m}, & b_{1},b_{2},b_{3}\in \mathbb{Z} \\ z_{m+1}=c_{1}x_{m}+c_{2}y_{m}+c_{3}z_{m}, & c_{1},c_{2},c_{3}\in \mathbb{Z} \end{matrix}\right.$
Conform acestui sistem ecuatia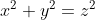 $x^{2}+y^{2}=z^{2}$ devine: 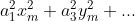$a_{1}^{2}x_{m}^{2}+a_{3}^{2}y_{m}^{2}+...$ = $(a_{1}^{2}+b_{1}^{2}-c_{1}^{2})x_{m}^{2}+...$ .
Pina la urma se ajunge la un sistem cu 9 necunoscute(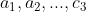 $a_{1},a_{2},...,c_{3}$ ) si 6 ecuatii.
Raspunsul final e: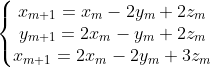 $\left\{\begin{matrix} x_{m+1}=x_{m}-2y_{m}+2z_{m}\\ y_{m+1}=2x_{m}-y_{m}+2z_{m}\\ x_{m+1}=2x_{m}-2y_{m}+3z_{m} \end{matrix}\right.$ (in carte e prezentat pentru un caz mai general).
Aceastai tot.

O idee posibila de rezolvare (aplicind gasirea solutiilor recursiv) ar fi: Aflind ca solutia minimala nu e naturala (pentru un anumit grad), se determina ca si celelalte solutii ce urmeaza la fel nu sunt naturale, ceea ce am demonstra ca ecuatia nu are solutii naturale pentru gradul dat.

Deci sa vedem daca ecuatia lui Fermat are solutii intregi pentru n=3,4,5,7,....
n=3.
$F^{3}\Leftrightarrow x^{3}+y^{3}=z^{3}\Leftrightarrow (x^{\frac{3}{2}})^{2}+(y^{\frac{3}{2}})^{2}=(z^{\frac{3}{2}})^{2}.$
Aplicind relatiile recursive (care s-au obtinut in sistem), indata comitem o greseala (pe care eu am comis-o). Deoarece nu trebue de uitat caci x,y,z apartin lui Z (lui N), in cazul dat ele apartin lui I.
Deci o concluzie putem trage in cazul dat: n trebue sa fie un numar par >2.

n=4.
$F^{4}\Leftrightarrow x^{4}+y^{4}=z^{4}\Leftrightarrow (x^{2})^{2}+(y^{2})^{2}=(z^{2})^{2}.$

Solutia minimala (subminimala), pentru orice grad este tripletul: (0,1,1) sau (1,0,1) [vom lucra mai departe cu (0,1,1), ca nu e gresit].
Adica $(x_{0}=0,y_{0}=1,z_{0}=1)$
Urmatoarea solutie (de aceasta data minimala nu subminimala), contine valori irationale, si ele sunt: $(x_{1}=\sqrt{3},y_{1}=2,z_{1}=\sqrt{5})$ .
La fel se determina caci si urmatoarea solutie tot contine valori irationale, apoi se (trebue) demonstreaza (ceea ce nu am facut-o, dar pare simplu), caci si celelalte la fel sunt irationale.
Deci pentru gradul 4 ecuatia F4 nu are solutii in N....

n=6
$F^{6}\Leftrightarrow x^{6}+y^{6}=z^{6}\Leftrightarrow (x^{3})^{2}+(y^{3})^{2}=(z^{3})^{2}$
Prima solutie minimala este: $(x_{1}=\sqrt[3]{3},y_{1}=\sqrt[3]{4},z_{1}=\sqrt[3]{5})$
La fel se observa ca celelalte sunt irationale, in cazul dat.

Pentru caz general, n=2t, la fel nu exista nici o solutie naturala, deoarece din solutia subminimala se obtine solutia minimala $(x_{1}=\sqrt[t]{3},y_{1}=\sqrt[t]{4},z_{1}=\sqrt[t]{5})$ , numerele 3,4,5 sunt consecutive, deci e imposibil sa existe vreun t unde sa se obtina solutii naturale. Sau, pentru asa valori mici (3,4,5,) , nu exista vreun t (>2), care sa se obita solutii naturale.

Problema ramine nerezolvata deoarece nu stiu ce metoda ar ajuta (in cazul dat) pentru celelalte grade (prime). La fel nu stiu daca in anii cei (cind s-a enuntat teorema) se stia foarte bine despre sisteme de ecuatii, matrici, etc.

Scris de **meteor** Vin 01 Iun 2012, 14:21

O posibila idee ar fi: Folosind acelasi algoritm de determinare a solutiei ecuatiei (pentru n>2) ca si la cazul 2 recursiv, (adica iarasi alcatuirea sistemului de ecuatii, gasirea necunoscutelor,...etc.). Gasirea solutiei ecuatiei pentru gradul dat (numere prime), devine mult mai usor determinarea daca sunt sau nu solutii naturale.
Apoi, pentru caz general (cind puterea e un oarecare numar prim).

Dar, aceasta nu ar fi asa usor de facut (cit spus), sunt necesare calcule bune, si sa fii un profesionist in sisteme si matrici.

Scris de **curiosul** Vin 01 Iun 2012, 14:43

Scris de **meteor** Vin 01 Iun 2012, 17:22

meteor a scris:... cu atit mai mult si pentru $k_{1},k_{2},...$

Ceea ce e citat, am gresit. Nicidecum nu inseamna caci si pentru gradele k1,k2,.... nu sunt solutii naturale.

Scris de **meteor** Vin 01 Iun 2012, 18:12

curiosul a scris: Eu iti propun sa o analizezi si altfel, atat timp cat te rezumi la valori naturale.

Adica nu analiza ecuatia in functie de n, ci in functie de x,y,z.

Adica, daca x,y,z sunt consecutive, pentru ce valori ale lui n ecuatia are solutii ?
Daca x>y>z, Iar diferenta dintre z si y este egala cu diferenta dintre y si x, pentru ce valori ale lui n ecuatia are solutii ?

$x^{n}+(x+1)^{n}=(x+2)^{n}.$ (1)
Cum s-a observat, e important ca x+y>z; x+z>y; y+z>x (ultimele 2 sunt inutile daca se spune ca x1 e valabil.
Dezvoltind binoamele din (1) am ajunjem la:
$x^{n}+x^{n}+C_{n}^{n-1}x^{n-1}+...+1=x^{n}+2C_{n}^{n-1}+...+2^{n}$
Daca x e un numar par atunci ecuatia se duce pe ripa, mai trebuie de verificat si celelalte cazuri. Daca analizezi triunghiul lui Pascal, observi ca permament exista un numar dublu de numere impare pe rinduri. Aceasta ar insemna ca in cazul cind n e impar, suma coeficientilor (inmultiti cu x) permament va fi un numar par. Insa, iarasi in partea stinga din (1) se observa ca partea stinga e un numar impar, partea dreapta a egalitatii e numar par, deci nu exista x ce sa apartina lui N.
Dar, nu are sens sa se analizeze si sa se pearda timpul in zadar, daca nu e o baza buna pusa. Cu ce premisa se porneste ca x,y,z trebue sa fie numere consecutive (la fel si pentru alte idei si propuneri de rezolvare) ?!

In cartea lui V.Suceveanu, mai e o metoda de rezolvare (mai e si in "Foae Matematica"), acolo este descris (calcule de pagini) cum se determina pentru fiecare grad, n=3,n=4,.. .
Problema e ca cu cit gradul creste calculele se maresc cu zeci de pagini. Plus ca nu prea vad (sau nu am inteles poate) cum se determina odata si odata pentru un grad general.

Mai am si eu chiteva metode personale (cei drept nefinisate).

Ce mi se pare foarte important in Metoda1 e ca am descris un algoritm de calcul, ce e drept foarte superficial.

Scris de **curiosul** Vin 01 Iun 2012, 19:18

Scris de **curiosul** Lun 04 Iun 2012, 17:35

Scris de **meteor** Lun 04 Iun 2012, 19:31

curiosul a scris:Vad ca esti foarte pasionat de aceasta teorema.
Incerc sa te ajut intr-un fel si sa-ti mai dau idei.

Interesul la aceasta teorema, mai mult a aparut in urma discutiei pe care am avut-o cu V.Suceveanu (cite ai perdut tu ca nu ai discutat cu el [el fiind un pasionat de teoria numerelor ]). Sincer sa fiu, mie nu prea i-mi place teoria numerelor.
Am sa-ti imprumut si eu niste idei Very Happy

.

curiosul a scris:
Deci incercam sa gasim solutiile naturale ale ecuatiei :
$x^{n}+y^{n}=z^{n}$

Notam y-x=s si z-x=t.
Deci putem rescrie ecuatia ca fiind:
$x^{n}+(x+s)^{n}=(x+t)^{n}$

Ti-am facut odata o observatie ca e import sa arati si ce domeniu apartine acele variabile care le introduci ( sa zicem pentru: 0 < x < y < z ; atunci t > s > 0 ) altfel poti scapa/gasi
greseala/solutia [dar pinace asta e fleac].

curiosul a scris:
Pentru s, t fixate, bineinteles naturale, putem arata ca solutiile x,y,z,n sunt unice.
Prin asta vreau sa spun ca daca exista o solutie a ecuatiei
$x^{n}+(x+s)^{n}=(x+t)^{n}$ ,
nu mai exista alta ecuatie de genul:
$(x')^{n'}+(x'+s)^{n'}=(x'+t)^{n'}$
$(x')^{n}+(x'+s)^{n}=(x'+t)^{n}$
$(x)^{n'}+(x+s)^{n'}=(x+t)^{n'}$
care sa aiba solutie pentru aceleasi valori s, t naturale.

De aici rezulta ca pentru orice valori s si t, interpretate in contextul de mai sus,
ecuatia lui Fermat are solutie in gradul 2, ea nu poate avea solutii in alt grad mai mare ( nu luam in calcul gradul 1).
Deja anulezi din start, foarte multe situatii in care ecuatia nu poate avea solutii pentru n mai mare ca 2.

Ar trebui sa mai arati ca pentru combinatia (s,t) care nu apare ca solutie in gradul al doilea, nu pot aparea nici in alt grad.

Oricum ar fi, exista o unicitate a solutiilor in functie de s si t.

Daca nu intelegi ce vreau sa spun pe undeva si ai nevoie de lamuriri suplimentare sau chiar ajutor sa demomnstrezi ceva in acest sens, cat imi sta in putere si sunt capabil, te ajut cu placere.

Cum nu ai da (in propunerea ta), dar tu tot 3 variabile ai (sub grad) [daca am inteles{mai corect spus nimic nu am inteles}, despre s si t ], plus (la caz general) il mai ai si pe gradul (ca variabila).
Chiar, nu prea am inteles ce vreai sa faci cu aceasta idee. Sa scapi de 2 variabile si sa ajungi la una singura, astfel mult mai usor se rezolva ecuatia.
Si cum le gasesti tu pe s,t (fixe)?
Ai mai spus:
"Oricum ar fi, exista o unicitate a solutiilor in functie de s si t."
Cum?! De unde ai ajuns la aceasta concluzie?

Scris de **curiosul** Lun 04 Iun 2012, 20:16

Scris de **meteor** Lun 04 Iun 2012, 20:34

[completare la metoda1] V.Suceveanu (cind vorbea despre Marea teorema a lui Fermat) spunea:
"Stiind solutia minima, se pot determina toate celelalte solutii".
Nu i-mi ese din cap.

[ma gindesc, e gresit oare parerea ce urmeaza?!] Dar poate e valabila formula de obtinere a solutiilor recursive si pentru valori nenaturale (adica pentru x,y,z irationale, despre cele rationale nici o trebuinta nu avem)?

Acestea se pot determina/demonstra poateca astfel.
1) (pentru valori rationale/ irationale):
fie vom da valori rationale lui x,y,z, irationale. Apoi vom inlocui si verifica formula recursiva.
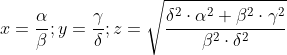
$x=\frac{\alpha }{\beta };y=\frac{\gamma }{\delta };z=\sqrt{\frac{\delta ^{2}\cdot \alpha ^{2}+\beta ^{2}\cdot \gamma ^{2}}{\beta ^{2}\cdot \delta ^{2}}}$

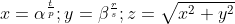
$x=\alpha ^{\frac{t}{p}};y=\beta ^{\frac{r}{s}}; z=\sqrt{x^{2}+y^{2}}$
Fie aceasta e o solutie oarecare (solutia n).
Daca, formula recursiva e valabila pentru valori irationale, atunci, recursiv, trebue la fel sa fie adevarata urmatoarea solutie(solutia n+1).
Acum ne ramine de inlocuit in formula
Daca (x_n+1)^2+(y_n+1)^2=(z_n+1)^2, atunci e (adevarat?!) ca si pentru valori irationale e valabil.

Ceea ce ne-ar permite foarte usor sa demonstram ca si pentru cazul cind gradele iau valori impare ecuatia la fel nu are solutii in N.

Scris de **curiosul** Lun 04 Iun 2012, 21:00

Scris de **meteor** Lun 04 Iun 2012, 23:19

Ei nu curiosule, tu ce crezi V.S. a scris povesti?!
E adevarata formula pentru gradul II.
Eu caut in cazul dat legatura cu torema lui Fermat (despre asta si a fost discutia).
Ce nu stiu precis (ma mai gindesc) daca e veridica formula de obtinere a solutiilor recursiv si pentru valorile lui x,y,z real pozitive.

Se pareca totul merge bine.
Deci, am luat un caz absolut particular.
Fie exista asa o solutie: x0=1/2; y0=1/4; z0=sqrt(x^2+y^2)=sqrt(5)/4.
Inlocuim aceasta in formula.
Obtinem: x1=sqrt(5)/2; y1=(3+2sqrt(5))/4;
z1=(2+3sqrt(5))/4.
Intradevar, x1^2+y1^2=z1^2.

Scris de **curiosul** Mar 05 Iun 2012, 08:27

Scris de **CAdi** Vin 28 Sept 2012, 13:14

Liniştita lume a matematicienilor a fost tulburată de un cercetător care susţine că a reuşit să rezolve una dintre cele mai importante probleme ale teoriei numerelor. Matematicianul Shinichi Mochizuki, de la Universitatea Kyoto din Japonia a eliberat un raport de 500 de pagini în care susţine că a demonstrat “conjectura abc”.

Conjectura abc a fost propusă independent de David Masser şi Joseph Oesterle în 1985 este una dintre cele mai importante teorii. "Dacă ea va fi validată va rezolva dintr-o lovitură numeroase probleme diofantine, printre care se numără şi Ultima Teoremă a lui Fermat. În cazul în care se dovedeşte că Mochizuki are dreptate, atunci aceasta va fi cea mai mare realizarea matematică din secolul XXI", a declarat matematicianul Dorian Goldfeld de la Universitatea Columbia.

Conjectura conţine numeroase probleme diofantine printre care şi Ultima Teoremă a lui Fermat (x la puterea n plus y la puterea n este diferit de z la puterea n unde x,y,z sunt numere întregi iar n este mai mare de 2), enunţată de savantul francez în secolul al XVII-lea şi care, timp de sute de ani, a rămas o enigmă pentru matematicienii din întreaga lume.

De-a lungul timpului, mulţi matematicieni au încercat să demonstreze conjectura. În 2007, matematicianul francez Lucien Szpiro, a cărui muncă din 1978 a condus la crearea ulterioară a conjecturii abc, a susţinut că ar fi găsit o rezolvare. Cu toate acestea, în scurt timp s-a demonstrat că explicaţia lui nu poate fi validă.

Pentru acest proiect, Mochizuki a dezvoltat tehnici pe care doar puţini matematicieni le înţeleg şi care implică noi "obiecte" matematice (entităţi abstracte similare cu exemple mai familiare precum obiecte geometrice, permutaţii şi matrice). "Până acum, el este singurul care înţelege în totalitate acest proiect", a declarat Goldfeld.

Conform profesorului Brian Conrad lucrarea lui Mochizuki oferă noi perspective care nu vor fi acceptate cu uşurinţă de comunitate. Cercetarea matematicianului nipon este publicată sub formă a patru lucrări lungi care fac referire la alte studii mai vechi, ceea ce înseamă că verificarea teoriei va dura destul de mult. Cu toate acestea, se pare că abilitatea sa de a demonstra teoreme este recunoscută de mulţi matematicieni ca urmare a lucrărilor sale anterioare.

"Pe lângă faptul că este posibil să se fi găsit o soluţie la conjectura abc, cu adevărat spectaculos este faptul că aceste tehnici, utilizate de Mochizuki în demonstraţie, ar putea fi instrumente foarte puternice pentru rezolvarea unor viitoare probleme din teoria numerelor".

Sursa: Nature

Scris de **meteor** Lun 01 Oct 2012, 14:57

Cel mai simplu, este sa rezolvi o problema prin metode cit posibil mai complicate, iar cel mai complicat este sa rezolvi o problema prin metode cit posibil mai elementare.

Scris de **Dacu** Vin 01 Feb 2013, 09:27

O idee de rezolvare:
Din $Marea teorema a lui Fermat. Mimetex$ rezultă că $Marea teorema a lui Fermat. Mimetex.cgi?{x^n=z^n-y^n=(z-y) \cdot (z^{n-1}+z^{n-2} \cdot y+.....$ ceea ce înseamnă că $Marea teorema a lui Fermat. Mimetex.cgi?{x=a \cdot (z-y)=b \cdot (z^{n-1}+z^{n-2} \cdot y+.....$ .
Prin simetrie rezultă şi faptul că $Marea teorema a lui Fermat. Mimetex.cgi?{y=c \cdot (z-x)=d \cdot (z^{n-1}+z^{n-2} \cdot x+.....$ .
În ambele cazuri $Marea teorema a lui Fermat. Mimetex$ .
Este adevărat ce spun eu şi dacă da atunci la ce ar ajuta această idee? Rolling Eyes

Scris de **curiosul** Vin 01 Feb 2013, 10:53

Scris de **Dacu** Vin 01 Feb 2013, 12:18

Cred că ai greşit ceva pe undeva căci nu cred că din relaţiile mele nu cred că rezultă ceea ce spui tu şi anume:
$\dpi{150} \mathbf{(z-y)^{n-1}= (z^{n-1}+z^{n-2} \cdot y+......+z \cdot y^{n-2}+y^{n-1})}$ .
Cum a rezultat relaţia de mai sus?

Scris de **curiosul** Vin 01 Feb 2013, 14:11

Scris de **curiosul** Vin 01 Feb 2013, 15:09

Scris de **curiosul** Vin 01 Feb 2013, 20:59

Scris de **curiosul** Vin 01 Feb 2013, 22:15

Scris de **curiosul** Sam 02 Feb 2013, 13:58

Scris de **curiosul** Sam 02 Feb 2013, 16:39

Scris de **curiosul** Sam 02 Feb 2013, 17:21

Scris de **Dacu** Dum 03 Feb 2013, 08:40

curiosul a scris:De fapt nu este chiar atat de greșit,
iar mai corect ar fi :

dacă $\dpi{150} \mathbf{x^n=z^n-y^n=(z-y) \cdot (z^{n-1}+z^{n-2} \cdot y+......+z \cdot y^{n-2}+y^{n-1})}$

atunci $\dpi{150} \mathbf{(z-y)^{kn-1}= (z^{n-1}+z^{n-2} \cdot y+......+z \cdot y^{n-2}+y^{n-1})}$

pentru că s-ar ajunge la

$\dpi{150} \mathbf{x^n=(z-y)(z-y)^{kn-1}=(z-y)^{kn}=((z-y)^k)^n}$

adică $\dpi{150} \mathbf{x=(z-y)^k}$

Ce crezi, e corect așa ?

Sau poți să găsești un contra exemplu, pentru care să existe soluții ale ecuației pentru n=2, dar care să nu valideze raționamentul de mai sus ?
Pentru că după aia, ar fi mai ușor de stabilit pentru ce valori ale lui n ar fi posibil.

k este număr natural?Dacă da,atunci care sunt valorile pe care le poate lua k? Question

Scris de **curiosul** Dum 03 Feb 2013, 09:03

Scris de **meteor** Lun 11 Feb 2013, 23:11

1. Triunghiurile posibile stau in sectoarele AOC si ACB (fara OB si AB) , triunghiuri obtuzunghice si ascutitunghice. AD este latura z cea mai mare fiind. Restul.., punctul care e pe sectoarele spuse, de la acest punct pina la A este fie latura x, si de la acest punct la D este latura y.

Deasemenea valoarea lui x pentru un anumit grad n, trebue sa inceapa de la o anumita valoare minima posibile, in caz contrar deja devine indemnat ca ecuatia sa nu aiba solutii [pe mine am sa o spun].
< Mai departe stop blocaj.. >

Scris de **Dacu** Vin 01 Mar 2013, 09:08

Se ştie că în cazul în care $Marea teorema a lui Fermat. Mimetex$ şi dacă numerele prime între ele $Marea teorema a lui Fermat. Mimetex$ atunci aceste numere naturale prime între ele şi diferite de zero trebuie să reprezinte laturile unui triunghi şi ca atare trebuie să găsim relaţii intre laturile acelui triunghi care să ne conducă la eventualele soluţii.Deasemeni se observă foarte uşor că toate funcţiile trigonometrice cosinus,sinus,etc sunt numere raţionale şi bazându-ne şi pe acest fapt se poate demonstra uşor că pentru $Marea teorema a lui Fermat. Mimetex$ Marea Teoremă a lui Fermat nu are soluţii în mulţimea numerelor naturale diferite de zero şi prime între ele.Sper să nu fi greşit pe undeva calculele sau raţionamentul.Mai verific o dată şi sper ca azi să postez demonstraţia mea.

Scris de Continut sponsorizat

Marea teorema a lui Fermat.

Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.

Re: Marea teorema a lui Fermat.