Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Meteorr Ieri la 21:34
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Joi 21 Noi 2024, 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la virgil în Fiinte deosebite.
( 1 )
» Mesaj de la virgil în Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
( 1 )
» Mesaj de la CAdi în Sa mai auzim si de bine in Romania :
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| Dacu2 | ||||
| eugen | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Abel Cavaşi |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| virgil | ||||
| Dacu2 | ||||
| Meteorr | ||||
| ilasus | ||||
| CAdi | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 58 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 58 Vizitatori :: 1 Motor de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
O demonstrație elementară pentru Marea teoremă a lui Fermat
4 participanți
Pagina 1 din 1
 O demonstrație elementară pentru Marea teoremă a lui Fermat
O demonstrație elementară pentru Marea teoremă a lui Fermat
Se pare că se poate dezvolta o demonstrație elementară, deși este o idee mai complicat pentru cazul n=4
De vreo două zile tot analizez o demonstrație pe care am găsit-o pentru teorema lui Fermat și nu am găsit nicio greșeală.
Raționamentul este extrem de simplu pentru cazul n=p prim impar și mai mult, se poate verifica foarte ușor corectitudinea acestuia.
Este bazat într-o oarecare măsură pe factorizarea numerelor, domeniu pe care l-am analizat foarte mult.
Acest model de demonstrare a Marii teoreme a lui Fermat susține în egală măsură conjectura Beal, care spune că ecuația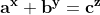 are soluții pentru x, y, z strict mai mari ca 2, doar dacă a, b, c au un divizor comun. Pentru cazul în care exponenții sunt egali, x=y=z=n>2, conjectura Beal este de fapt o versiune a marii teoreme a lui Fermat, care spune că ecuația
are soluții pentru x, y, z strict mai mari ca 2, doar dacă a, b, c au un divizor comun. Pentru cazul în care exponenții sunt egali, x=y=z=n>2, conjectura Beal este de fapt o versiune a marii teoreme a lui Fermat, care spune că ecuația  nu are soluții întregi x, y, z pentru n mai mare ca 2.
nu are soluții întregi x, y, z pentru n mai mare ca 2.
Ecuația are soluții x, y, z având un divizor comun, doar dacă are soluții x', y', z' toate prime între ele, pentru că simplificând ecuația prin divizorul comun al soluțiilor x, y, z ori de câte ori este necesar, se ajunge la soluțiile prime între ele x', y', z' , ca și soluții ale ecuației.
are soluții x, y, z având un divizor comun, doar dacă are soluții x', y', z' toate prime între ele, pentru că simplificând ecuația prin divizorul comun al soluțiilor x, y, z ori de câte ori este necesar, se ajunge la soluțiile prime între ele x', y', z' , ca și soluții ale ecuației.
Prin conjectura Beal ecuația are soluții doar dacă x, y, z au un divizor comun, însă ecuația admite în primul rând soluții primitive.
are soluții doar dacă x, y, z au un divizor comun, însă ecuația admite în primul rând soluții primitive.
Prin urmare, demonstrând că ecuația are soluții întregi doar dacă x, y, z au un divizor comun, teorema lui Fermat este demonstrată, pentru că ar însemna să nu aibă soluții primitive, ceea ce este imposibil simplificând prin divizorul lor comun.
are soluții întregi doar dacă x, y, z au un divizor comun, teorema lui Fermat este demonstrată, pentru că ar însemna să nu aibă soluții primitive, ceea ce este imposibil simplificând prin divizorul lor comun.
Demonstrația de mai jos, este strict bazată pe acest raționament, ce poate fi generalizat pentru cazul n=p, unde p este număr prim impar și cazul n=4, pentru că dacă n nu este prim, el se divide fie cu un număr prim impar, fie doar cu puteri de doi. O putere de doi mai mare ca 2 este un multiplu de 4, în concluzie este necesar și suficient să analizăm doar cazurile n= p prim impar și n=4.
Plecăm de la condiția obligatorie ce trebuie îndeplinită între soluțiile ecuației : (x+y) > z.
Firește nu analizam cazul trivial, în care una din soluțiile x sau y este nulă. Dacă x și y sunt nenule, atunci z > y și vom nota soluția z=y+k.
Înlocuind în inegalitatea anterioară exprimarea soluției z ca fiind x+k, obținem :
(x+y) > z ; x+y > y+k, x > k. De la această inegalitate vom nota de asemenea, soluția x=k+q.
Înainte de a continua, precizăm faptul că k și y nu pot avea niciun factor comun, cu excepția lui 1, desigur.
Dacă k și y au un factor comun m, m mai mare ca 1, ar însemna că z și y au același factor comun m, pentru că k=z-y.
Dacă z-y și y au un factor comun, atunci z și y au de asemenea, acel factor comun.
Dacă k și y nu au factori comuni, evident, k și y+k nu au factori comuni.
Vom analiza în continuare ecuația prin aceste soluții x=k+q, y, z=y+k.
Demonstrăm pentru început cazul n=p prim impar, pentru că demonstrația este mai simplă și ușoară de înțeles și verificat, și o să las cazul n=4 la final pentru că raționamentul este o idee mai complicat.
Așadar, rescriem ecuația pentru cazul n=p prim impar și soluțiile de mai sus :
^p+y^p=(k+y)^p})
Vom analiza separat cazul n=3, pentru că dezvoltarea acestuia conține mai puțini termeni și se poate urmări și înțelege mai ușor raționamentul demonstrației.
^3+y^3=(k+y)^3})
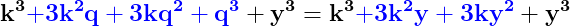
=3ky(y+k)}})
Observăm ca în partea dreaptă apare factorul k.
Termenul din stânga se poate divide cu k doar dacă q se divide cu k. Presupunând că q nu se divide cu k, în paranteza din stânga, k poate fi scos factor comun din primii doi termeni, iar dacă q nu se divide cu k, atunci paranteza respectivă nu se divide cu k.
În concluzie, dacă termenul din dreapta se divide cu k, atunci obligatoriu q se divide cu k. Notăm q=ks și rescriem ecuația :
+(ks)^2)=3ky(y+k)}})
=3ky(y+k)}})
=3ky(y+k)}})
=3y(y+k)}})
În această situație, termenul din stânga este cel care se divide cu k la pătrat. Dar k și y, precum și k și y+k nu au factori comuni.
Chiar dacă 3 este egal cu k, în stânga apare la puterea a doua, iar în dreapta doar la puterea întâi. De aici rezultă că egalitatea este posibilă doar dacă k și y, sau k și y+k au un factor comun. Dacă oricare dintre y și y+k au un factor comun cu k, acel factor comun este factorul comun al lui z și y, așa cum am arătat la început. Dacă z și y au un factor comun, atunci prin egalitatea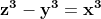 prin scoaterea factorului comun al lui z și y, rezultă că și x trebuie să aibă acel factor comun.
prin scoaterea factorului comun al lui z și y, rezultă că și x trebuie să aibă acel factor comun.
Deci pentru cazul n=3, ecuația are soluții întregi doar dacă x, y, z au un factor comun.
Situație imposibilă pentru că ecuația trebuie să aibă soluții prime între ele.
În continuare, demonstrăm cazul general n=p prim impar exact pe același principiu, nu înainte de a menționa faptul că în dezvoltarea binomului^p}) unde p este număr prim, toți termenii cu excepția lui
unde p este număr prim, toți termenii cu excepția lui 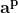 și
și 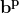 se divid cu p, dacă a și b nu se divid cu p:
se divid cu p, dacă a și b nu se divid cu p:
^p=a^p+\frac{p}{1}a^{p-1}b+\frac{p(p-1)}{1\cdot&space;2}a^{p-2}b^2+...+\frac{p(p-1)...(p-r+1)}{1\cdot2\cdot&space;...\cdot&space;r&space;}a^{p-r}b^r+...+b^p})
Pentru că p fiind un număr prim, acesta nu este divizibil, deci poate fi scos factor comun din oricare ceilalți termeni cu excepțiile corespunzătoare.
Rescriem ecuația pentru cazul general p :
^p+y^p=(y+k)^p})
Folosind dezvoltarea de mai sus, vom proceda ca în cazul de mai sus pentru n=3, simplificând inițial cu k și y la puterea p, scoatem factorul comun q în stânga și factorul pky în partea dreaptă, într-o manieră simplificată ecuația va deveni :
=p\cdot&space;k\cdot&space;y(k\cdot&space;t+y^{p-2})})
Ca și în cazul pentru n=3, în dreapta apare factorul k, iar termenul din stânga se divide cu k doar dacă q se divide cu k. Dacă q se divide cu k, notând q=ks' din dezvoltarea binomului^p}) și eliminând k la puterea p care va apărea în dezvoltarea binomului din dreapta, va apărea în partea stângă k la puterea p.
și eliminând k la puterea p care va apărea în dezvoltarea binomului din dreapta, va apărea în partea stângă k la puterea p.
Continuând raționamentul ca în cazul n=3, rezultă că una din valorile y sau kt +y se divide cu k.
Dacă oricare din acestea două se divide cu k, însemnă că y și k au un factor comun, de unde rezultă și că y și z au factorul comun pe care-l au k și y.
Dacă z și y au un factor comun, x îl va avea de asemenea, iar în concluzie, pentru cazul general n=p prim impar, ecuația are soluții doar dacă x, y și z au un factor comun.
Situație imposibilă pentru că ecuația trebuie să aibă soluții primitive x, y, z.
Cazul n=4.
^4+y^4=(y+k)^4}})
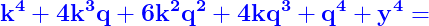
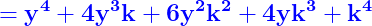
Simplificăm cu y la puterea a patra și k la puterea a 4, iar egalitatea devine :
=2ky(2y^2+3ky+2k^2)}})
Observăm că în partea dreaptă apare k factor, ceea ce înseamnă că în termenul din stânga trebuie să-l avem de asemenea pe k factor.
Dar în stânga, k poate apărea factor doar dacă q se divide cu k. Presupunem că q nu se divide cu k. În paranteza din stânga, il putem scoate factor pe k din primii trei termeni și rămâne termenul q la puterea a treia. Dacă acesta nu se divide cu k, înseamnă că în paranteza din stânga k nu poate fi scos factor comun, iar termenul din stânga nu s-ar divide cu k. Însă acesta trebuie obligatoriu să apară în factorizarea termenului din stânga, iar aceasta este posibil doar dacă q se divide cu k. Notăm q=ks și înlocuim :
=2ky(2y^2+3ky+2k^2)}})
^2&space;+(ks)^3&space;)=2ky(2y^2+3ky+2k^2)}})
=2ky(2y^2+3ky+2k^2)}})
Simplificăm egalitatea prin k
=2y(2y^2+3ky+2k^2)}})
Observăm că dacă q se divide cu k, în partea stângă apare k la puterea a treia factor, dar nu mai apare în dreapta.
Așa cum am menționat în partea de început, k și y nu pot avea factori comuni. În paranteza din dreapta poate fi scos k factor comun din ultimii doi termeni și rămâne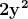 . Pentru că y și k nu au factori comuni, din paranteza termenului din dreapta poate fi scos factor comun 2. Dar k trebuie să fie la puterea a treia factorul termenului din dreapta, iar dacă k are și alți factori cu excepția lui 2, atunci acești factori nu pot apărea în termenul din dreapta, pentru că k și y nu au factori comuni. Deci k se divide cu 2 obligatoriu. Rescriem ecuația inițială :
. Pentru că y și k nu au factori comuni, din paranteza termenului din dreapta poate fi scos factor comun 2. Dar k trebuie să fie la puterea a treia factorul termenului din dreapta, iar dacă k are și alți factori cu excepția lui 2, atunci acești factori nu pot apărea în termenul din dreapta, pentru că k și y nu au factori comuni. Deci k se divide cu 2 obligatoriu. Rescriem ecuația inițială :
^4-y^4=(k+q)^4})
Dezvoltând binomul termenului din stânga, simplificând ulterior cu y la puterea a patra, dacă k este un număr par, din toți termenii din stânga care rămân poate fi scos 2, factor comun. Deci termenul din dreapta trebuie să se dividă cu 2, ceea ce înseamnă că q+k trebuie să fie un număr par. Pentru că k este par, q+k este par doar dacă și q este par. Deci soluția x trebuie să fie o soluție pară.
Dar folosind tot raționamentul de mai sus, exprimând soluția z în funcție de x, z=x+k' și y=k'+q', se ajunge la aceeași concluzie, adică y=k'+q' este o soluție pară. Deci x și y sunt ambele numere pare, iar prin suma puterilor lor z va fi de asemenea, un număr par.
Deci în cazul n=4, ecuația are soluții doar dacă acestea se divid toate cu 2.
Deci s-a ajuns la concluzia că soluțiile presupuse inițial ca fiind prime între ele, sunt toate divizibile cu 2.
Contradicție !
Ceea ce era de demonstrat !
Există cu siguranța demonstrații mult mai simple pentru cazul n=4, dar am dezvoltat-o pe aceasta pentru a susține enunțul conjecturii Beal.
Ce zici Geza ?
Am verificat raționamentul de foarte multe ori, vreo două zile la rând aproape că n-am mai dormit și n-am găsit o greșeală așa cum cam fac de obicei. Chiar n-am găsit. Dar, cine știe, poate că și aici e vreo greșeală care-mi scapă, datorată probabil și oboselii.
Mai mult, pentru cazul n=p, odată înțeleasă, demonstrația este extrem de simplă și ușor de verificat corectitudinea raționamentului.
Este adevărat că în cazul n=4 raționamentul este ceva mai costisitor, dar se datorează faptului că în dezvoltarea binomului pentru exponentul 4, cu excepțiile corespunzătoare, nu toți termenii se divid cu 4, ca și în cazul n=p prim impar.
De vreo două zile tot analizez o demonstrație pe care am găsit-o pentru teorema lui Fermat și nu am găsit nicio greșeală.
Raționamentul este extrem de simplu pentru cazul n=p prim impar și mai mult, se poate verifica foarte ușor corectitudinea acestuia.
Este bazat într-o oarecare măsură pe factorizarea numerelor, domeniu pe care l-am analizat foarte mult.
Acest model de demonstrare a Marii teoreme a lui Fermat susține în egală măsură conjectura Beal, care spune că ecuația
Ecuația
Prin conjectura Beal ecuația
Prin urmare, demonstrând că ecuația
Demonstrația de mai jos, este strict bazată pe acest raționament, ce poate fi generalizat pentru cazul n=p, unde p este număr prim impar și cazul n=4, pentru că dacă n nu este prim, el se divide fie cu un număr prim impar, fie doar cu puteri de doi. O putere de doi mai mare ca 2 este un multiplu de 4, în concluzie este necesar și suficient să analizăm doar cazurile n= p prim impar și n=4.
Plecăm de la condiția obligatorie ce trebuie îndeplinită între soluțiile ecuației : (x+y) > z.
Firește nu analizam cazul trivial, în care una din soluțiile x sau y este nulă. Dacă x și y sunt nenule, atunci z > y și vom nota soluția z=y+k.
Înlocuind în inegalitatea anterioară exprimarea soluției z ca fiind x+k, obținem :
(x+y) > z ; x+y > y+k, x > k. De la această inegalitate vom nota de asemenea, soluția x=k+q.
Înainte de a continua, precizăm faptul că k și y nu pot avea niciun factor comun, cu excepția lui 1, desigur.
Dacă k și y au un factor comun m, m mai mare ca 1, ar însemna că z și y au același factor comun m, pentru că k=z-y.
Dacă z-y și y au un factor comun, atunci z și y au de asemenea, acel factor comun.
Dacă k și y nu au factori comuni, evident, k și y+k nu au factori comuni.
Vom analiza în continuare ecuația prin aceste soluții x=k+q, y, z=y+k.
Demonstrăm pentru început cazul n=p prim impar, pentru că demonstrația este mai simplă și ușoară de înțeles și verificat, și o să las cazul n=4 la final pentru că raționamentul este o idee mai complicat.
Așadar, rescriem ecuația pentru cazul n=p prim impar și soluțiile de mai sus :
Vom analiza separat cazul n=3, pentru că dezvoltarea acestuia conține mai puțini termeni și se poate urmări și înțelege mai ușor raționamentul demonstrației.
Observăm ca în partea dreaptă apare factorul k.
Termenul din stânga se poate divide cu k doar dacă q se divide cu k. Presupunând că q nu se divide cu k, în paranteza din stânga, k poate fi scos factor comun din primii doi termeni, iar dacă q nu se divide cu k, atunci paranteza respectivă nu se divide cu k.
În concluzie, dacă termenul din dreapta se divide cu k, atunci obligatoriu q se divide cu k. Notăm q=ks și rescriem ecuația :
În această situație, termenul din stânga este cel care se divide cu k la pătrat. Dar k și y, precum și k și y+k nu au factori comuni.
Chiar dacă 3 este egal cu k, în stânga apare la puterea a doua, iar în dreapta doar la puterea întâi. De aici rezultă că egalitatea este posibilă doar dacă k și y, sau k și y+k au un factor comun. Dacă oricare dintre y și y+k au un factor comun cu k, acel factor comun este factorul comun al lui z și y, așa cum am arătat la început. Dacă z și y au un factor comun, atunci prin egalitatea
Deci pentru cazul n=3, ecuația are soluții întregi doar dacă x, y, z au un factor comun.
Situație imposibilă pentru că ecuația trebuie să aibă soluții prime între ele.
În continuare, demonstrăm cazul general n=p prim impar exact pe același principiu, nu înainte de a menționa faptul că în dezvoltarea binomului
Pentru că p fiind un număr prim, acesta nu este divizibil, deci poate fi scos factor comun din oricare ceilalți termeni cu excepțiile corespunzătoare.
Rescriem ecuația pentru cazul general p :
Folosind dezvoltarea de mai sus, vom proceda ca în cazul de mai sus pentru n=3, simplificând inițial cu k și y la puterea p, scoatem factorul comun q în stânga și factorul pky în partea dreaptă, într-o manieră simplificată ecuația va deveni :
Ca și în cazul pentru n=3, în dreapta apare factorul k, iar termenul din stânga se divide cu k doar dacă q se divide cu k. Dacă q se divide cu k, notând q=ks' din dezvoltarea binomului
Continuând raționamentul ca în cazul n=3, rezultă că una din valorile y sau kt +y se divide cu k.
Dacă oricare din acestea două se divide cu k, însemnă că y și k au un factor comun, de unde rezultă și că y și z au factorul comun pe care-l au k și y.
Dacă z și y au un factor comun, x îl va avea de asemenea, iar în concluzie, pentru cazul general n=p prim impar, ecuația are soluții doar dacă x, y și z au un factor comun.
Situație imposibilă pentru că ecuația trebuie să aibă soluții primitive x, y, z.
Cazul n=4.
Simplificăm cu y la puterea a patra și k la puterea a 4, iar egalitatea devine :
Observăm că în partea dreaptă apare k factor, ceea ce înseamnă că în termenul din stânga trebuie să-l avem de asemenea pe k factor.
Dar în stânga, k poate apărea factor doar dacă q se divide cu k. Presupunem că q nu se divide cu k. În paranteza din stânga, il putem scoate factor pe k din primii trei termeni și rămâne termenul q la puterea a treia. Dacă acesta nu se divide cu k, înseamnă că în paranteza din stânga k nu poate fi scos factor comun, iar termenul din stânga nu s-ar divide cu k. Însă acesta trebuie obligatoriu să apară în factorizarea termenului din stânga, iar aceasta este posibil doar dacă q se divide cu k. Notăm q=ks și înlocuim :
Simplificăm egalitatea prin k
Observăm că dacă q se divide cu k, în partea stângă apare k la puterea a treia factor, dar nu mai apare în dreapta.
Așa cum am menționat în partea de început, k și y nu pot avea factori comuni. În paranteza din dreapta poate fi scos k factor comun din ultimii doi termeni și rămâne
Dezvoltând binomul termenului din stânga, simplificând ulterior cu y la puterea a patra, dacă k este un număr par, din toți termenii din stânga care rămân poate fi scos 2, factor comun. Deci termenul din dreapta trebuie să se dividă cu 2, ceea ce înseamnă că q+k trebuie să fie un număr par. Pentru că k este par, q+k este par doar dacă și q este par. Deci soluția x trebuie să fie o soluție pară.
Dar folosind tot raționamentul de mai sus, exprimând soluția z în funcție de x, z=x+k' și y=k'+q', se ajunge la aceeași concluzie, adică y=k'+q' este o soluție pară. Deci x și y sunt ambele numere pare, iar prin suma puterilor lor z va fi de asemenea, un număr par.
Deci în cazul n=4, ecuația are soluții doar dacă acestea se divid toate cu 2.
Deci s-a ajuns la concluzia că soluțiile presupuse inițial ca fiind prime între ele, sunt toate divizibile cu 2.
Contradicție !
Ceea ce era de demonstrat !
Există cu siguranța demonstrații mult mai simple pentru cazul n=4, dar am dezvoltat-o pe aceasta pentru a susține enunțul conjecturii Beal.
Ce zici Geza ?
Am verificat raționamentul de foarte multe ori, vreo două zile la rând aproape că n-am mai dormit și n-am găsit o greșeală așa cum cam fac de obicei. Chiar n-am găsit. Dar, cine știe, poate că și aici e vreo greșeală care-mi scapă, datorată probabil și oboselii.
Mai mult, pentru cazul n=p, odată înțeleasă, demonstrația este extrem de simplă și ușor de verificat corectitudinea raționamentului.
Este adevărat că în cazul n=4 raționamentul este ceva mai costisitor, dar se datorează faptului că în dezvoltarea binomului pentru exponentul 4, cu excepțiile corespunzătoare, nu toți termenii se divid cu 4, ca și în cazul n=p prim impar.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Pe un principiu aproape asemănător cu cel de mai sus, cred că se poate demonstra și conjectura lui Beal, dar într-un loc am o anumită incertitudine.
Dacă reușesc să o elimin, conjectura lui Beal se poate demonstra la fel de elementar.
Cred că vor urma alte câteva nopți albe.
Dacă reușesc să o elimin, conjectura lui Beal se poate demonstra la fel de elementar.
Cred că vor urma alte câteva nopți albe.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Am tot analizat conjectura Beal pe principii asemănătoare celei de mai sus și am ajuns la concluzia că există o greșeală subtilă, aproape insesizabilă în demonstrația de mai sus care face ca raționamentul că fie incomplet.
Pentru cei care nu stăpânesc bine teoria numerelor, cât și pentru cei care nu au aprofundat destul de mult această mare teoremă lui Fermat, greșeala din demonstrația de mai sus este foarte greu de identificat.
Nu mă refer la exprimări incomplete, ci la logica raționamentului.
Dar am reușit s-o corectez.
Am acum 100% o demonstrație elementară corectă pentru marea teoremă a lui Fermat.
Pentru că, după cum se pare, cam vorbesc singur pe aici, i-o voi spune aceluia care va găsi greșeala pentru care demonstrația de mai sus nu este corectă, sau mai degrabă incompletă.
Problema este că raționamentul nu poate fi folosit și pentru conjectura Beal. Există o diferență enormă între ceea ce spune teorema lui Fermat și ceea ce vrea să spună conjectura Beal, aceasta din urmă fiind mult mai importantă în teoria numerelor.
Aștept părerile, de orice natură, ale celor interesați de subiect.
Pentru cei care nu stăpânesc bine teoria numerelor, cât și pentru cei care nu au aprofundat destul de mult această mare teoremă lui Fermat, greșeala din demonstrația de mai sus este foarte greu de identificat.
Nu mă refer la exprimări incomplete, ci la logica raționamentului.
Dar am reușit s-o corectez.
Am acum 100% o demonstrație elementară corectă pentru marea teoremă a lui Fermat.
Pentru că, după cum se pare, cam vorbesc singur pe aici, i-o voi spune aceluia care va găsi greșeala pentru care demonstrația de mai sus nu este corectă, sau mai degrabă incompletă.
Problema este că raționamentul nu poate fi folosit și pentru conjectura Beal. Există o diferență enormă între ceea ce spune teorema lui Fermat și ceea ce vrea să spună conjectura Beal, aceasta din urmă fiind mult mai importantă în teoria numerelor.
Aștept părerile, de orice natură, ale celor interesați de subiect.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Salut
Am citit ce ai scris inca de luni dar nu este o lectura usoara,am zis ca revin si o mai revad odata inainte de a emite o parere dar crezi ca am mai revenit ?
M-am luat cu alte subiecte care nu necesita efort.
Sunteti mai multi interesati de acest tip de probleme de ce nu va uniti eforturile?
Eu am picat in mijlocul lor ca si musca in lapte nu este domeniul meu "favorit"
O sa-l iau la "tranta" si daca gasesc greseala revin
Am citit ce ai scris inca de luni dar nu este o lectura usoara,am zis ca revin si o mai revad odata inainte de a emite o parere dar crezi ca am mai revenit ?
M-am luat cu alte subiecte care nu necesita efort.
Sunteti mai multi interesati de acest tip de probleme de ce nu va uniti eforturile?
Eu am picat in mijlocul lor ca si musca in lapte nu este domeniul meu "favorit"
O sa-l iau la "tranta" si daca gasesc greseala revin
Vizitator- Vizitator
 Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Curiosule, nu pot să-ți spun decât un lucru. De fiecare dată, dar absolut de fiecare dată, când am zis în viața asta că am ceva 100% corect, am mai găsit după o vreme câte o greșeală.
E imposibil în genul ăsta de muncă, ideea e să nu fie greșeli evidente și atât de grave încât să distrugă tot. În rest, numai cine nu muncește, nu greșește, iar cine muncește mult, greșește mult.
Bethe, un mare, mare fizician, a spus că expert într-un domeniu e acea persoană care a făcut toate greșelile, și a fost completat de alt deștept, Wheeler, care a zis că de aceea trebuie să ne străduim să facem toate greșelile cât mai repede.
E imposibil în genul ăsta de muncă, ideea e să nu fie greșeli evidente și atât de grave încât să distrugă tot. În rest, numai cine nu muncește, nu greșește, iar cine muncește mult, greșește mult.
Bethe, un mare, mare fizician, a spus că expert într-un domeniu e acea persoană care a făcut toate greșelile, și a fost completat de alt deștept, Wheeler, care a zis că de aceea trebuie să ne străduim să facem toate greșelile cât mai repede.

omuldinluna- Ne-a părăsit
- Mulţumit de forum : Prenume : Omul




Numarul mesajelor : 2728
Puncte : 30683
Data de inscriere : 03/08/2011
Obiective curente : Doresc sa termin expunerea problemei clasice a miscarii in camp central, cu aplicatie la campul gravitational Newtonian
 Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Fals.omuldinluna a scris:Curiosule, nu pot să-ți spun decât un lucru. De fiecare dată, dar absolut de fiecare dată, când am zis în viața asta că am ceva 100% corect, am mai găsit după o vreme câte o greșeală.
E imposibil în genul ăsta de muncă, ideea e să nu fie greșeli evidente și atât de grave încât să distrugă tot. În rest, numai cine nu muncește, nu greșește, iar cine muncește mult, greșește mult.
Bethe, un mare, mare fizician, a spus că expert într-un domeniu e acea persoană care a făcut toate greșelile, și a fost completat de alt deștept, Wheeler, care a zis că de aceea trebuie să ne străduim să facem toate greșelile cât mai repede.
Nu e totul chiar oriunde aceeasi.
Nu in cazul lui curiosul.
Dupa cite presupun, el are de rezolvat intii de toate ceva probleme de viata.. si apoi restul perde- vreme.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Tu ai introdus o multime de parametri, includerea unui parametru in problema, necesita deseori ca mai apoi sa "scapi" de el, dar nu e asa de usor de "scapat".curiosul a scris:
...........
Vom analiza separat cazul n=3, pentru că dezvoltarea acestuia conține mai puțini termeni și se poate urmări și înțelege mai ușor raționamentul demonstrației.
Observăm ca în partea dreaptă apare factorul k.
Termenul din stânga se poate divide cu k doar dacă q se divide cu k {nu is convins de acestea spuse}. Presupunând că q nu se divide cu k, în paranteza din stânga, k poate fi scos factor comun din primii doi termeni, iar dacă q nu se divide cu k, atunci paranteza respectivă nu se divide cu k.
În concluzie, dacă termenul din dreapta se divide cu k {el chiar se divide cu k}, atunci obligatoriu q se divide cu k {nu is convins, ca nu am analizat bine, dar de o fi asa, atunci ar reesi ca ecuatia fermantica are solutii in N pentru puterea n= 3 ?!}. Notăm q=ks și rescriem ecuația {s - trebue sa apartina lui N, si in asa caz trebue mai apoi sa ajungem la absurd} :
În această situație, termenul din stânga este cel care se divide cu k la pătrat {nu e chiar corect spus. Simpulu: termenul din stinga se divide cu k. }. Dar k și y, precum și k și y+k nu au factori comuni.
Chiar dacă 3 este egal cu k {?! Nu pricep:x }, în stânga apare la puterea a doua, iar în dreapta doar la puterea întâi. De aici rezultă că egalitatea este posibilă doar dacă k și y, sau k și y+k au un factor comun. Dacă oricare dintre y și y+k au un factor comun cu k, acel factor comun este factorul comun al lui z și y, așa cum am arătat la început. Dacă z și y au un factor comun, atunci prin egalitateaprin scoaterea factorului comun al lui z și y, rezultă că și x trebuie să aibă acel factor comun.
Deci pentru cazul n=3, ecuația are soluții întregi doar dacă x, y, z au un factor comun.
Situație imposibilă pentru că ecuația trebuie să aibă soluții prime între ele.
Din ce retin, tu ai introdus la sfirsit pe parametrul s (presupun desigur ca e natural).
Si se admite ca ecuatia ar avea solutii.
Spre sfirsit trebue sa ajungi la absurd, fie ca s e nenatural fie alte chestii- trestii.
Eu insa nu observ.
In linii mari, cred ca ecuatia :
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Foarte frumos spus,dar depinde ce fel de greşeli facem căci dacă facem mereu aceleaşi greşeli atunci asta nu este bine.....omuldinluna a scris:Bethe, un mare, mare fizician, a spus că expert într-un domeniu e acea persoană care a făcut toate greșelile, și a fost completat de alt deștept, Wheeler, care a zis că de aceea trebuie să ne străduim să facem toate greșelile cât mai repede.
Seneca a spus:
"Errare humanum est , sed perseverare diabolicum.".
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22433
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
În primul rând vă mulțumesc tuturor pentru răspunsuri.
Pentru Dacu și meteor, deoarece ei vor să sublinieze în mesajele lor o idee comună, în deosebi raportat la caracterul meu, voi începe răspunzându-le lor.
Voi încerca să nu vă stimulez să alunecăm în replici raportate la personalitatea fiecăruia, nefolositoare de altfel.
Să nu uităm înainte de toate că acesta este un forum de cercetare.
După care vă mai spun că eu analizez efectiv fundamentul.
Adică...numerele.
Că nu lucrez cu funcții, primitive, derivate, integrale și alte alea ce țin de o algebră analitică este pentru că nu le consider din punctul meu de vedere ca aparținând teoriei numerelor.
Acest răspuns este pentru meteor, pentru că eu am înțeles exact ce vrea el să spună.
Pentru Dacu, partea plină a paharului în a persevera în greșeală implică o mai bună cunoaștere și înțelegere a ceea ce fac eu.
Și mai mult, pentru că în multe din cazuri, tot eu am fost și cel care a arătat ulterior greșeala, unul din motive fiind chiar să nu trimit pe piste false cititorii, mai mult, ei putând învăța din greșelile mele.
Ca și concluzie raportată strict la subiect, greșeala menționată de meteor nu este aceea.
AȘA CUM AM SPUS, GREȘEALA ESTE APROAPE INSESIZABILĂ.
V-aș ruga pe amândoi să înțelegeți că acest tip de greșeală vă poate folosi amândurora pe viitor.
Eu perseverez în greșeală, dar nu remarcați faptul că greșesc în probleme care a chinuit secole mințile oamenilor. Mi se pare normal să nu fie chiar atât de ușor și în raționamentele pe care le folosesc să fie strecurate greșeli.
Mi-aș dori, înainte să mă judecați, să-mi arătați că sunteți capabili să identificați greșeala.
Omuldinlună.
Ce să mai...mulțumesc pentru încurajări, mulțumesc pentru faptul că mă înțelegi și-ți demonstrezi încă o dată valoarea.
Pentru faptul că ești capabil să tratezi orice situație ca atare și la adevărata ei valoare.
Tu ai înțeles de mult că sunt "mic" , dar ai înțeles și că mă străduiesc la nesfârșit și nu renunț ușor.
Mulțumesc încă o dată.
Geza.
Foloseam numele tău când te-am întrebat pentru că tu erai singurul care-și mai dădea cu părerea la ce spun eu pe aici în ultimul timp.
Cum am spus, greșeala este foarte greu de depistat.
Raționamentul este perfect valid cu excepția unei situații pe care nu o ia în calcul și care face ca demonstrația să fie incompletă.
Pentru moment mă abțin să vorbesc despre ea, pentru că cel care va găsi greșeala va înțelege bine și complet și demonstrația corectată.
Repet, raționamentul este perfect valid cu o singură excepție de la regulă.
Pentru Dacu și meteor, deoarece ei vor să sublinieze în mesajele lor o idee comună, în deosebi raportat la caracterul meu, voi începe răspunzându-le lor.
Voi încerca să nu vă stimulez să alunecăm în replici raportate la personalitatea fiecăruia, nefolositoare de altfel.
Să nu uităm înainte de toate că acesta este un forum de cercetare.
După care vă mai spun că eu analizez efectiv fundamentul.
Adică...numerele.
Că nu lucrez cu funcții, primitive, derivate, integrale și alte alea ce țin de o algebră analitică este pentru că nu le consider din punctul meu de vedere ca aparținând teoriei numerelor.
Acest răspuns este pentru meteor, pentru că eu am înțeles exact ce vrea el să spună.
Pentru Dacu, partea plină a paharului în a persevera în greșeală implică o mai bună cunoaștere și înțelegere a ceea ce fac eu.
Și mai mult, pentru că în multe din cazuri, tot eu am fost și cel care a arătat ulterior greșeala, unul din motive fiind chiar să nu trimit pe piste false cititorii, mai mult, ei putând învăța din greșelile mele.
Ca și concluzie raportată strict la subiect, greșeala menționată de meteor nu este aceea.
AȘA CUM AM SPUS, GREȘEALA ESTE APROAPE INSESIZABILĂ.
V-aș ruga pe amândoi să înțelegeți că acest tip de greșeală vă poate folosi amândurora pe viitor.
Eu perseverez în greșeală, dar nu remarcați faptul că greșesc în probleme care a chinuit secole mințile oamenilor. Mi se pare normal să nu fie chiar atât de ușor și în raționamentele pe care le folosesc să fie strecurate greșeli.
Mi-aș dori, înainte să mă judecați, să-mi arătați că sunteți capabili să identificați greșeala.
Omuldinlună.
Ce să mai...mulțumesc pentru încurajări, mulțumesc pentru faptul că mă înțelegi și-ți demonstrezi încă o dată valoarea.
Pentru faptul că ești capabil să tratezi orice situație ca atare și la adevărata ei valoare.
Tu ai înțeles de mult că sunt "mic" , dar ai înțeles și că mă străduiesc la nesfârșit și nu renunț ușor.
Mulțumesc încă o dată.
Geza.
Foloseam numele tău când te-am întrebat pentru că tu erai singurul care-și mai dădea cu părerea la ce spun eu pe aici în ultimul timp.
Cum am spus, greșeala este foarte greu de depistat.
Raționamentul este perfect valid cu excepția unei situații pe care nu o ia în calcul și care face ca demonstrația să fie incompletă.
Pentru moment mă abțin să vorbesc despre ea, pentru că cel care va găsi greșeala va înțelege bine și complet și demonstrația corectată.
Repet, raționamentul este perfect valid cu o singură excepție de la regulă.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Nu am răspuns de fapt, la nedumeririle lui meteor.
Fie numerele a*b și c.
Suma sau diferența lor se divide cu un număr prim p.
Dacă c se divide cu p, atunci suma sau diferența numerelor a*b și c se divide cu p, doar dacă unul dintre numerele a sau b se divide cu c.
Celelalte explicații derivă efectiv din această regulă, pe care ai menționat-o și tu la un moment dat nu știu prin ce subiect.
Crede-mă, tot ceea ce ai subliniat, nu reprezintă contraargumentele corespunzătoare, corecte și pe care vreau să le aud.
Reține că așa cum ai analizat tu nu știu ce funcții sau altceva, dar foarte bine, așa am analizat eu factorizarea numerelor.
Oricum, ia fiecare nelămurire în parte, nu toate într-un mesaj, și o să-ți explic de ce nu pot fi considerate greșeli.
Fie numerele a*b și c.
Suma sau diferența lor se divide cu un număr prim p.
Dacă c se divide cu p, atunci suma sau diferența numerelor a*b și c se divide cu p, doar dacă unul dintre numerele a sau b se divide cu c.
Celelalte explicații derivă efectiv din această regulă, pe care ai menționat-o și tu la un moment dat nu știu prin ce subiect.
Crede-mă, tot ceea ce ai subliniat, nu reprezintă contraargumentele corespunzătoare, corecte și pe care vreau să le aud.
Reține că așa cum ai analizat tu nu știu ce funcții sau altceva, dar foarte bine, așa am analizat eu factorizarea numerelor.
Oricum, ia fiecare nelămurire în parte, nu toate într-un mesaj, și o să-ți explic de ce nu pot fi considerate greșeli.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Mai sus este o greșeală din neatenție :curiosul a scris:
Fie numerele a*b și c.
Suma sau diferența lor se divide cu un număr prim p.
Dacă c se divide cu p, atunci suma sau diferența numerelor a*b și c se divide cu p, doar dacă unul dintre numerele a sau b se divide cu c.
doar dacă unul dintre numerele a sau b se divide cu p, nu cu c.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
Re: O demonstrație elementară pentru Marea teoremă a lui Fermat
meteor a scris:
Tu ai introdus o multime de parametri, includerea unui parametru in problema, necesita deseori ca mai apoi sa "scapi" de el, dar nu e asa de usor de "scapat".
Din ce retin, tu ai introdus la sfirsit pe parametrul s (presupun desigur ca e natural).
Si se admite ca ecuatia ar avea solutii.
Spre sfirsit trebue sa ajungi la absurd, fie ca s e nenatural fie alte chestii- trestii.
Eu insa nu observ.
In linii mari, cred ca ecuatia :(cu cutarele date reesite din problema), nu se rezolva in N asa de simplu.
Chiar dacă am introdus o mulțime de parametrii, soluționarea problemei nu implică neapărat eliminarea lor, ci stabilirea unor relații între acești parametrii pentru care egalitatea la care se ajunge nu poate fi corectă.
Și în N chiar se rezolvă așa simplu. Pentru că termenii unei egalități, în numere naturale, trebuie să conțină toți factorii primi în descompunerea lor, precum și aceleași puteri ale acestor factori primi.
Dacă unul din termeni se divide doar cu k, iar celălalt se divide cu k la pătrat, egalitatea nu este posibilă în N.
Este ceea ce am subliniat în raționamentul folosit.
Am citit cu atenție ce ai menționat și nu acestea sunt greșelile.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Subiecte similare
Subiecte similare» Marea teorema a lui Fermat.
» Marea Teorema a lui Fermat
» Demonstrația algebrică a marii teoreme a lui Fermat
» Marea Teorema a lui Fermat
» Demonstrația algebrică a marii teoreme a lui Fermat
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 