Demonstrația algebrică a marii teoreme a lui Fermat

Demonstrația algebrică a marii teoreme a lui Fermat

"Pentru ecuația nu are soluții întregi. "

Vom demonstra Marea teorema a lui Fermat prin Mica teorema a lui Fermat.

Dacă are soluții naturale, ecuația are și soluții întregi x, y, z, deci se rezumă la analiza soluțiile naturale x, y, z, nenule diferite cu (x+y) > z > y >x.
Dacă ecuația are soluții, atunci ecuația are soluții x, y, z prime între ele, pentru acea valoare a lui n și vom analiza în continuare aceste soluții primitive (prime între ele).
Dacă n nu este un număr prim, atunci n=ab, a,b>1, ceea ce înseamnă că dacă pentru n nonprim ecuația admite soluțiile x, y, z atunci ecuația admite soluțiile atât pentru a, cât și pentru b :



Deci ne putem rezuma la a analiza ecuația doar valorile lui n ca fiind numere prime.
Cazul particular îl reprezintă n=4, care trebuie analizat separat, pentru că există soluții pentru n=2.
Dacă pentru n=4 ecuația nu are soluții, atunci nu are soluții pentru nicio putere de 2 mai mare ca 4, dar trebuie analizat cazul n=4, pentru că ecuația are soluții pentru cazul n=2.

Așadar, vom analiza inițial cazul pentru care n=p, unde p este un număr prim impar.
Dacă niciuna din soluțiile x, y, z ale ecuației nu se divide cu numărul prim p, atunci putem folosi Mica Teorema a lui Fermat și anume prin faptul că dacă n este un număr prim p, atunci



Deci dacă x, y, z sunt naturale care nu se divid cu p, atunci există a, b, c naturale astfel încât :



Din sistemul de mai sus obținem egalitatea :





De aici rezultă că (x+y-z) se divide cu p.

Putem arăta că (x+y-z) se divide cu p prin altă modalitate care nu impune condiția ca x, y, z să nu fie divizibile cu p.
Formulăm o lemă și demonstrăm folosind teorema lui Wilson că :



Ecuația o scriem ca diferență și anume :





Dacă p este un număr prim impar, atunci p-1 este un număr par.
Dacă p-1 este un număr par, atunci atunci în descompunerea lui z și x la puterea p-1 apar cu semnul +.
În paranteza mare din dreapta scădem și adunăm termenii corespunzători pentru a obține .
Din lema demonstrată mai sus se ajunge la :
(eocamdată nu voi scrie toată dezvoltarea pentru că nu avem nevoie de ea acum)





În mod asemănător, precedăm și cu



și ajungem la





Dar să revenim la analiza prin Mica teoremă a lui Fermat.
Deci dacă am arătat că dacă x, y, z nu se divid cu p , x+y-z se divide cu p.
Dacă x, y, z, p sunt soluțiile naturale ale ecuației, atunci











Din mica teoremă a lui Fermat rezultă deasemenea că se divide cu p, dacă z nu se divide cu p, ceea ce înseamnă că trebuie să se dividă de asemenea cu p dacă termenul din stânga egalității se divide cu p, iar primul termen al sumei se divide cu p.
Aceasta din urmă se poate demonstra în felul următor .







Dacă x și y nu se divid cu p, deci nici (x+y) nu se divide cu p, ceea ce înseamnă că se divide cu p, deci din cantitatea de mai sus poate fi scos p factor comun, iar se divide cu p.

În acest caz avem trei diferențe care se divid cu p :



Dacă (x+y)> z (ca și soluții ale ecuației), atunci toate trei relațiile sunt posibile doar dacă , unde k este natural.
Dar ca și soluții x, y, z ale ecuației, trebuie să avem deasemenea (x+y) > z > y > x, deci de asemenea trebuie să avem inegalitatea :







Dacă y este mai mare ca x, amândouă naturale, egalitatea de mai sus nu are soluții k, p naturale.
Contradicție, plecând de la presupunerea că toate necunoscutele introduse în analiză sunt naturale.

În mesajele viitoare, voi arăta cazurile în care una din necunoscutele x, y, z se divide cu p și cazul n=4.
Pentru cazul n=4 am o demonstrație bazată pe congruența modulo 4 și 8, dar vreau să văd dacă reușesc una mai simplă.

De fapt demonstrația și mai simplă pentru n=p (p număr prim impar este următoarea) :

-pentru z natural mai mare ca 1 și p număr prim,
din mica teoremă a lui Fermat rezultă că
se divide cu p.

-pentru oricare x y, z naturale, mai mari ca 1,
soluții ale ecuației ,
se divide cu p :













Ambii termeni ai sumei de mai sus se divid cu p, deci



Dacă (x+y) > z > y > x, atunci relațiile sistemului de mai sus sunt adevărate doar dacă (x+y)=z(kp+1), cu k natural, deci







Dar pentru că y este mai mare ca x, atunci cel puțin una din valorile k sau p nu sunt naturale.

Contradicție, dacă plecăm de la presupunerea că x, y, z sunt naturale.
Deci pentru n un număr prim impar, ecuația nu are soluții naturale.

Mai trebuie să arat cazul n=4.
O să-l scriu mâine.

În paranteza de mai sus care îl conține pe p factor, am uitat să inversez semnele termenilor, dar nu schimbă concluzia.
Oricum, faptul că



rezultă mai simplu prin congruența în mod p, a puterilor p lui x și y.

Dar dacă p este un număr prim impar rezultă deasemenea că, atât z la puterea p, cât și suma puterilor p a lui x și y sunt un multiplu de (x+y).
Asta înseamnă că z și (x+y) au cel puțin un factor comun, ca și soluții ale ecuației.
Mai trebuie analizat dacă z și (x+y) au factorul comun p, sau cum se schimbă situația în cazul în care z și (x+y) au un factor comun.
Trebuie analizat dacă în această situație se respectă condiția ca (x+y)=z(kp+1) cu k natural.

Am arătat în prima postare din acest subiect că .
Atunci există k natural astfel încât x+y-z=pk.
Rescriem ecuația pentru n un număr prim impar, separând în expresia de mai sus soluțiile pentru fiecare în parte :



Analizând prima relație, trecem termenul în dreapta și desfacem paranteza pa puterea p din stânga. Observăm că în această dezvoltare cu excepția termenului din toți ceilalți termeni poate fi scos (z-y) factor comun. În dreapta, poate fi scris de asemenea cu (z-y) factor comun. Trecem în dreapta toți termeni cu excepția lui , și scoatem (z-y) factor comun.
De aici rezultă că kp și (z-y) au cel puțin un factor comun, fie p, fie, k, fie unul din factorii care divide k, dacă acesta nu este prim.

În mod asemănător, procedăm cu a doua relație din sistemul de mai sus și ajungem de asemenea, la a arăta că kp și (z-x) au cel puțin un factor comun, fie p, fie, k, fie unul din factorii care divide k, dacă acesta nu este prim.

De asemenea, din a treia relație putem separa kp la puterea p de o parte și (x+y) factor comun în cealaltă parte, de unde rezultă că kp și (x+y) au cel puțin un factor comun, fie p, fie, k, fie unul din factorii care divide k, dacă acesta nu este prim.

Deci avem :



În orice fel am analiza, ajungem în situația ca cel puțin două dintre parantezele din dreapta egalității, se divide fie cu p, fie cu k, fie cu unul din divizorii lui k, dacă acesta nu este prim.

Sa presupunem ca (z-y) și (x+b) se divide cu a (a este unul din divizorii lui k).
Atunci avem



Dacă atât (x+y) , cât și (z-y) se divid cu a, pentru că în ambele cazuri termenul din dreapta egalității se divide cu a, atunci x și z au factorul comun a, ceea ce este imposibil, pentru că x, y, z sunt prime între ele.
La fel se ajunge în orice fel am analiza oricare din cele trei egalități cu kp, din sistemul de mai sus.

Rămâne să găsesc o demonstrație mai simplă pentru cazul n=4, după care voi scrie demonstrația completă.

Cazul n=p (p este un număr prim impar)

"Pentru p un număr prim impar , ecuația nu are soluții x,y,z întregi, nenule, diferite și prime între ele"









În același mod arătăm că .
Dacă p este un număr impar (prim) atunci





Așadar, avem :



În continuare, vom arăta că



Indiferent că x, sau, y, sau z se divid sau nu cu p, din mica teoremă a lui Fermat rezultă că :



Deci există astfel încât



Din ecuația inițială rezultă că







Din relația de mai sus putem concluziona că :



Revenim la sistemul inițial :



unde înlocuim valorile din parantezele din dreapta egalităților cu cele echivalente ale sistemului anterior și obținem :



Analizând fiecare relație din al doilea sistem rezultă că :

1. -Parantezele din dreapta egalităților trebuie să conțină cel puțin un factor comun al termenului din stânga
2. -Pentru că 1. trebuie să fie adevărat, iar în suma sau diferența din paranteza din dreapta egalităților sistemului de mai sus se gasește termenul din stânga, rezultă că celălalt termen din parantezele din dreapta trebuie să fie divizibil cu termenul din stânga și care se află de asemenea în suma sau diferența parantezelor respective din dreapta.

Din 1. și 2. rezultă că k=xyzk'

Deci







Dacă x, y, z sunt nenule diferite, termenul din dreapta este mai mare ca cel din stânga.
Egalitatea de mai sus este posibilă dacă cel puțin una din necunoscutele egalității de mai sus este o fracție ireductibilă sau un număr irațional.
Dar toate necunoscutele introduse în demonstrație sunt numere întregi !
Apare o contradicție din care rezultă într-un final că una din valorile x,y,z,p nu sunt numere întregi.

Ceea ce era de demonstrat !

Voi prezenta mai târziu cazul n=4, care este singurul caz necesar de demonstrat pentru a face o demonstrație completă a teoremei.

Aș fi curios dacă este cineva care nu este de acord și care nu înțelege demonstrația pentru n=p (p număr prim).
I-aș explica personal, cât mă pricep, iar dacă există cineva îl rog să deschidă un subiect separat unde vom vorbi acolo.

Voi reveni cu cazul n=4, dar vreau să găsesc o demonstrație la fel de ușor de înțeles.

La demonstrația de mai sus, mai trebuie totuși adăugat ceva.
Și analizăm doar una din relații pentru că este valabil pentru oricare celelalte două. Să luăm una care conține diferența, spre exemplu, (x-pk).

P este un număr prim, rezultă că x și p nu au factori comuni mai mari ca 1.
Pentru ca x^p și (x-pk) au cel puțin un factor comun, rezultă că x și k au un factor comun, să spunem.
Deci



Simplificând cu , rezultă că dacă a' este un divizor a lui x, iar (a'-pa") trebuie să conțină cel puțin un factor comun a lui sau a', iar p este prim ;i considerând cel mai mare divizor comun a lui x și k, rezultă că

ceea ce este imposibil.

De aici rezultă că k este un multiplu de x și raționamentul din postarea anterioară este valabil.

Deci pentru n=p, p număr prim impar, teorema lui Fermat este adevărată.

Raționamentul n=p prezentat mai sus este incomplet. Am găsit o exprimare a binomului lui Newton care poate ajuta și este mult mai eficientă în analiza marii teoreme a lui Fermat.
Dar este nevoie de o demonstrație solidă că pentru n un număr prim, binomul lui Newton pentru care exponentul este un număr prim, are pentru orice număr prim aceea dezvoltare. Dar implică distribuția numerelor prime și nu este chiar atât de simplu. Și în acest caz, în toate încercările pe care le-am făcut dezvoltarea binomului lui Newton are aceeași structură, iar coeficienții puterilor au legătură cu distribuția numerelor prime.

Oricum, pentru cazul n=4, cea mai simplă demonstrație pe care am reușit să dezvolt este următoarea :









Din forma de mai sus în care este adusă ecuația rezultă că x și y nu pot fi ambele impare. Dacă ambele ar fi impare, termenul din stânga îl conține factor pe 4, pentru că x, y, și z sunt două numere impare și unul par. Dacă x și y ar fi ambele impare în termenul din stânga apare factor 4, iar în termenul din dreapta doar 2. Deci fie x, fie y este un număr par, ceea ce înseamnă că z este un număr impar.
Se poate arăta de asemenea că cele două paranteze ale termenului din stânga nu pot avea alți factori comuni cu excepția lui 2.
Presupunem că cele două paranteze ar factor comun un număr a impar și o putere de 2 mai mare ca 2 :











De aici rezultă că dacă s este mai mare ca 1 atunci z se divide cu 2, ceea ce nu este posibil pentru că z este un număr impar, deci cele două paranteze din stânga nu pot avea factor comun o putere de 2 mai mare ca 2.

Analizând factorul comun a, se ajunge la :









Deci dacă atât se divide cu a, cât și se divide cu a, rezultă că termenul din stânga îl conține pe a factor, pentru că a este un număr impar, rezultă că fie x, fie y se divide cu a, ceea ce este imposibil pentru că ar însemna că atât z se divide cu a, cât și x sau y, iar x,y,z sunt numere prime între ele.

Deci cele două paranteze, cu excepția lui 2 nu pot avea alți factori comuni, iar x și y sunt prime între ele.
Pentru fiecare din cele două paranteze se divide cu 2, iar doar una din valorile x sau y se divide cu 2, atunci singura situație posibilă este cea în care una din paranteze este egală cu , dacă este numărul par, iar cealaltă paranteză este egală cu 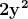dacă y este numărul impar.
În orice situație, fie că x este un numărul par, fie că y este numărul par, una din paranteze este egală, fie cu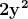 , fie cu în funcție de care dintre x și y este impar.

Egalând cele două paranteze, fie cu , fie cu 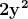, observăm că niciuna din situații nu este posibilă pentru că z>y>x :



situație imposibilă, sau



situație din nou imposibilă.

Deci pentru cazul n=4, teorema lui Fermat este adevărată, iar pentru orice n un multiplu de 4 ecuația nu are soluții pentru că :



Iar dacă n este egal cu 4 ecuația nu are soluții.
Rămâne situația în care n este un număr prim p.
Pentru p=3,5,7 pot să demonstrez la fel de simplu că ecuația nu are soluții, dar nu pot demonstra deocamdată cazul general n=p, p număr prim impar, deși am o pistă foarte interesantă, bazată pe dezvoltarea binomului lui Newton, în cazul în care exponentul acestuia este prim, dar cum spuneam, este strâns legată de distribuția numerelor prime și nu este chiar atât de ușor.
Dar merită încercat, pentru că este posibil să ajung la o concluzie interesantă în ceea ce privește distribuția numerelor prime.

Voi prezenta scurt și demonstrația cazului n=3.
Deci x, y, z sunt prime între ele :









De aici rezultă că x și (z-y) au un factor comun. Se poate observa de asemenea că cele două paranteze ale ale termenului din dreapta egalității îl pot avea doar pe 3 factor comun.
Dacă 3 nu este factorul lor comun, atunci cele două paranteze sunt numere prime între ele pentru că zy și (z-y) nu pot avea factori comuni atât timp cât z și y sunt prime între ele.
Putem să stabilim în egală măsură că dacă 3 este factorul comun al celor două paranteze, atunci (z-y) îl conține factor pe 3 la puterea 3k-1, unde k este natural nenul, deoarece în partea stângă a egalității trebuie să-l avem la puterea 3, iar în paranteza pătrată din dreapta el poate fi scos factor comun doar la puterea întâi.
Dacă cele două paranteze ale termenului din dreapta sunt numere prime între ele, atunci (z-y) este un număr la puterea 3.
Dar nu ne vom folosi de aceste observații, pentru a demonstra cazul n=3 al ecuației.
Ideea este că le-am prezentat pentru că aceste observații sunt general valabile pentru orice n=p al ecuației, asupra cărora voi reveni în alt subiect, raportat la o relație cu distribuția numerelor prime.
Ceea ce reținem de aici este doar că x și (z-y) au un divizor comun.
Raționamentul este identic pentru



de unde concluzionăm că y și (z-x) au un divizor comun.
Dar acesta este diferit de divizorul pe care îl au în comun x și (z-y), pentru că dacă acești doi divizori ar avea vreun factor comun, ar însemna că x și y au de asemenea același factor comun.
În același mod arătăm și că



deci și în acest caz, z și (x+y) au un divizor comun care nu are niciun factor comun cu cel al lui x și (z-y) sau cu cel al lui y și (z-x) pentru că x, y, z sunt prime între ele.

Deci putem concluziona că (x+y-z) se divide atât cu divizorul comun al lui z și (x+y), cu al x și (z-y), cât și cu cel al lui y și (z-x), pentru că aceștia la rândul lor sunt primi între ei deoarece x, y și z sunt numere prime între ele.
Și dezvoltăm în continuare ecuația inițială :













În termenul din stânga, doar în paranteza pătrată din stânga (cea roșie) poate fi scos factorul comun al lui x și (z-y) și a lui y și (z-x).

[b]Dar doar la puterea întâi.[b]

Iar în termenul din dreapta acești divizori apar la puterea a treia.
Deci termenii egalității au factorizare diferită, ceea ce înseamnă că egalitatea nu este posibilă.
Deci pentru cazul n=3 ecuația nu are soluții, ca de altfel pentru orice multiplu de 3.
Demonstrația este asemănătoare pentru cazul n=5 și n=7, cu mici alte adăugiri și ar putea fi generalizată pentru orice n=p, unde p este un număr prim impar,
dar trebuie să demonstrez mai întâi ceva esențial vis-a-vis de binomul lui Newton.
O să mai verific o dată demonstrația pentru a fi sigur că nu este strecurată vreo greșeală pe undeva.

Și totuși, raționamentul de mai sus este incomplet, dar sper că i-am găsit completarea.
Cel puțin pentru cazul n=3 și să verific dacă se respectă la celelalte cazuri.
Deci voi relua raționamentul. Ajungem inițial la :









În mod identic ajungem și la



și aproape similar ajungem și la



Dezvoltăm în continuare ecuația inițială :



















Dar avem de asemenea :



Unde putem înlocui în termenul din stânga :



Termenul din dreapta este întreg dacă x, y, z sunt întregi.
Dar termenul din stânga nu mai este. Și anume :



Din forma în care este exprimat termenul de mai sus (cel din stânga ecuației) rezultă că una din soluțiile x, y, z se divide cu 3. Oricare dintre ele se divide cu 3, la numitor apare cel puțin .
Simplificăm o dată cu 3 care apare în stânga, iar una din parantezele de la numărător trebuie să se dividă cu cel puțin .

Dar aceea paranteză este doar aceea corespunzătoare valorii x, sau y, sau z, care se divide cu 3, pentru că numai una din valorile x, y, z se divide cu 3, ele fiind prime între ele.
Vom analiza un singur caz pentru că este valabil pentru oricare dintre x, y, z am alege ca fiind soluția divizibilă cu 3. Să presupunem că aceea este z, iar asta înseamnă că trebuie să se dividă cel puțin cu .
Dar aceasta se divide doar cu 3, pentru că așa rezultă din egalitatea :



Dacă z se divide cu 3, atunci înseamnă că (x+y) se divide cu 3. Dacă (x+y) se divide cu 3, xy nu se divide cu 3 pentru că xy și (x+y) sunt prime între ele. Dacă xy și (x+y) nu ar fi prime între ele, atunci atât x, cât și y, s-ar divide amândouă cu divizorul comun care ar divide xy și (x+y).

Simplificând așadar cu încă un 3, cel care rezultă din , la numitor mai rămâne cel puțin un 3.
Celelalte două paranteze nu se pot divide cu 3, dacă z se divide cu 3, pentru că ar însemna că z și una dintre soluțiile x sau y, au același divizor comun 3.

Dacă la numitor apare 3 ca factor, iar la numărător nu apare, fracția este ireductibilă, deci nu este un număr întreg.
Asta ar însemna că de asemenea, nu este un număr întreg, dar aceasta nu este posibil dacă x, y, z sunt întregi.

O să mai verific o dată să văd dacă raționamentul are din nou vreo greșeală pe undeva.

curiosul a scris:
Dacă z se divide cu 3, atunci înseamnă că (x+y) se divide cu 3. Dacă (x+y) se divide cu 3, xy nu se divide cu 3 pentru că xy și (x+y) sunt prime între ele. Dacă xy și (x+y) nu ar fi prime între ele, atunci atât x, cât și y, s-ar divide amândouă cu divizorul comun care ar divide xy și (x+y).
...
O să mai verific o dată să văd dacă raționamentul are din nou vreo greșeală pe undeva.

Da, aceasta este demonstrația corectă a cazului n=3.
Aș corecta în citatul de mai sus din demonstrația anterioară că dacă z se divide cu 3, atunci x și y nu se divid cu 3 pentru că ele sunt prime între ele, iar z se divide cu 3 doar dacă (x+y) se divide cu 3. De aici rezultă concret că din paranteza respectivă, 3 poate fi scos factor comun doar la puterea întâi.

Este valabil pentru oricare din soluțiile x, sau y, sau z divizibilă cu 3.
Într-o oarecare măsură, raționamentul se poate extinde la toate numerele prime cu o condiție care trebuie demonstrată și pe care o să încerc s-o definesc.
Voi prezenta mai târziu cazul n=5.

Iar m-am zăpăcit !
Fracția este inversă și raționamentul nu mai este valabil.

Se poate arăta totuși, că pentru cazul n=3, una din soluții se divide cu 3 :

Ecuația poate fi scrisă în trei moduri :



Din fiecare exprimare, în partea dreaptă a egalităților, factorii reprezentați de cele două paranteze sunt fie numere prime între ele, fie singurul lor divizor comun este 3.
Considerând soluțiile x, y, z soluțiile primitive ale ecuației, deci (x,y,z)=1, în fiecare paranteză pătrată din dreapta egalităților factorul 3 poate fi scos doar la puterea 1.
De asemenea, dacă x,y,z sunt prime între ele, doar una din soluțiile x, y, z se poate divide cu 3. Fie x, fie y, fie z.
Asta înseamnă că cel puțin una din soluțiile x sau y nu se divide cu 3. Considerăm aceea soluție nedivizibilă cu 3, ca fiind x.
Raționamentul este valabil și în cazul în care am considera că soluția nedivizibilă cu 3 dintre x și y este y, pentru că în sistemul de mai sus se observă că ele au o exprimare asemănătoare.
Din presupunerea ca fiind adevărată egalitatea :



dacă x nu se divide cu 3, rezultă că (z-y) nu se divide cu 3, iar cele două paranteze, și sunt numere prime între ele.
Singurul lor divizor comun putând fi doar trei, dar nu este posibil pentru că am presupus că x este soluția care nu se divide cu 3.
Dacă cele două paranteze sunt prime între ele, atunci ele sunt numere la puterea a treia, factorii lui x de altfel.
Putem așadar, să egalăm cele două paranteze cu un numere la puterea a treia :



Aducem ultima egalitate, cea care rezultă din primele două, la o exprimare similară :





Pentru că termenul din stânga îl are pe 3 factor rezultă că trebuie să-l avem factor și în dreapta pentru a avea egalitatea.
Dacă produsul din dreapta se divide cu 3, atunci se divide cu 3.
Dacă se divide cu 3, atunci în partea dreapta a egalității factorul 3 apare la puterea a doua.
De aici rezultă că una din soluțiile z sau y (doar una dintre ele) este divizibilă cu 3.
Cu alte mici artificii, asemănător se poate arăta că pentru cazul n=p, p este număr prim impar, una din soluțiile ecuației se divide cu p.

Greșeala din cazul n=4 poate fi corectată. Și anume :









Dacă x, y, z ar fi două numere pare și unul impar, sau trei numere impare, atunci în cele două paranteze s-ar obține două numere impare, produsul lor fiind de asemenea un număr impar. Dar în partea dreaptă apare un număr par. Deci soluțiile x,y,z nu pot fi două pare și unul impar, sau toate trei impare. Deci rămâne situația în care unul dintre ele este par și două impare, sau toate trei pare.

Analizăm cazul în care toate sunt pare și scriem soluțiile x,y,z ca fiind produsul dintre un număr impar și cea mai mare putere de 2 care divide soluția respectivă :



unde x', y', z' sunt numere impare. Simplificând egalitatea cu cel mai mare divizor comun al puterilor de 2, una dintre valorile a,b,c va fi cel mai mare divizor comun, iar soluția respectivă va rămâne doar un număr impar. Să presupunem că este 2 la puterea a :



Aducând egalitatea de mai sus la forma anterioară :



unde x' este un număr impar, cele două paranteze din stânga sunt numere impare, pentru că ajungem la cazul în care două sunt pare și unul impar, iar în dreapta avem un număr par. Situația este din nou imposibilă. Deci singurul caz este acela în care două dintre soluții sunt impare și una pară.
Revenind la egalitatea inițială, cu notațiile x, y, z :



având două soluții impare și o soluție pară, dacă în dreapta x, și y ar fi ambele impare, atunci termenul din dreapta egalității îl are pe factor doar pe 2 la puterea întâi, în timp ce în produsul din stânga, apare factor 2 la puterea a doua, pentru că fie suma, fie diferența, fie orice combinație de sumă și diferență între trei numere din care unul este par și două impare, rezultatul va fi tot un număr par, iar produsul a două numere pare îl conține factor pe 4. Deci, fie x, y în partea dreaptă este un număr par. Presupunem că x este par. Atunci în partea dreaptă îl vom avea cel puțin pe 2 la puterea a treia factor, pentru că x este la puterea a doua, doi va apărea cel puțin la puterea a doua, care mai apare o dată la puterea întâi, ceea ce înseamnă că în partea dreaptă, 2 apare ca factor cel puțin la puterea a treia.
Dar vom arăta în continuare că în partea stângă, în fiecare paranteză 2 apare ca factor doar la puterea întâi.
Presupunem că cele două paranteze îl au ca factor pe 2 la puterea s, unde s este mai mare ca 1 :







Asta ar însemna că z se divide de asemenea cu 2, dacă s este mai mare ca 1. Am ajunge în situația în care x și z sunt ambele pare, iar y impar. Situație imposibilă așa cum am arătat mai sus.
Dacă s nu este mai mare ca 1, atunci fiecare paranteză din stânga îl conține ca factor doar pe 2 la puterea întâi, produsul lor conținându-l la puterea a doua, iar în dreapta, pentru că am considerat că x este numărul par, 2 apare factor cel puțin la puterea a treia.
Simplificând cu 4 egalitatea, ajungem așadar, să stabilim o egalitate între un număr par și unul impar.
Situație din nou imposibilă.
Deci pentru cazul n=4 ecuația nu are soluții, cum de altfel nu are pentru niciun n care este un multiplu de 4, pentru că s-ar ajunge tot la o ecuație cu n=4 , pentru care am arătat că nu are soluții :



Q.E.D

Din linkul postat de Mezei Geza în alt subiect :

Mezei Geza a scris:Asa din prima am gasit asta sper sa fie suficient:

Teorema restului

Restul împărţirii unui polinom prin binomul X – a este egal cu valoarea f (a) .

Observaţie

Această teoremă ne ajută să găsim restul împărţirii unui polinom oarecare prin binomul X – a fără a mai face împărţirea.

http://www.thegame.go.ro/Mate/Polinoame/POLIN%20%281%29.htm

putem analiza teorema lui Fermat pentru n un număr prim impar și prin teorema din linkul postat de Mezei Geza.

Ecuația poate fi scrisă :



Din teorema respectivă, împărțind fiecare termen al egalităților cu (z-y) și respectiv (z-x) egalitățile devin :







Din egalitățile de mai sus rezultă că atât x, cât și y, se divid cu p, ceea ce înseamnă că x și y nu sunt prime între ele, ci se divid cu p.
Dacă și x și y se divid cu p, rezultă că și z se divide cu p.

Deci pentru n=p, unde p este un număr prim impar, ecuația poate avea soluții doar dacă acestea se divid cu p.

Aceasta devine o imposibilitate pentru că ecuația trebuie să admită și soluții primitive prime între ele.

Cazul n=4 se poate demonstra identic.

Din linkul postat de Mezei Geza în alt subiect :

Mezei Geza a scris:Asa din prima am gasit asta sper sa fie suficient:

Teorema restului

Restul împărţirii unui polinom prin binomul X – a este egal cu valoarea f (a) .

Observaţie

Această teoremă ne ajută să găsim restul împărţirii unui polinom oarecare prin binomul X – a fără a mai face împărţirea.

http://www.thegame.go.ro/Mate/Polinoame/POLIN%20%281%29.htm

putem analiza teorema lui Fermat pentru n mai mare ca 2 și prin teorema din linkul postat de Mezei Geza.

Ecuația poate fi scrisă :



Din teorema respectivă, împărțind fiecare termen al egalităților cu (z-y) și respectiv (z-x) egalitățile devin :







Din egalitățile de mai sus rezultă că atât x, cât și y, se divid cu n, ceea ce înseamnă că x și y nu sunt prime între ele, ci se divid cu n, avându-l de asemenea ca divizor și pe y în cazul lui x și x în cazul lui y.
Dacă atât x, cât și y se divid cu n, rezultă că și z se divide cu n.

Deci pentru n>2, putem aplica teorema împărțirii cu rest a unui polinom cu nedeterminata z în cazul nostru, atât la z-x, cât și la z-y, de unde reiese că ecuația poate avea soluții doar dacă acestea se divid cu n.

Aceasta devine o imposibilitate pentru că ecuația trebuie să admită și soluții primitive prime între ele.

De fapt, am cam înțeles greșit această teoremă.
Ea vorbește despre rest și nu despre câtul împărțirii.
Situație în care o să trebuiască să reverific și demonstrația lui Mezei Geza.