Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de ilasus Astazi la 19:58
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la virgil în Ce anume "generează" legile fizice?
( 1 )
» Mesaj de la CAdi în OZN in Romania
( 1 )
» Mesaj de la CAdi în ChatGPT este din ce în ce mai receptiv
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| Dacu2 | ||||
| eugen | ||||
| Forever_Man | ||||
| Abel Cavaşi | ||||
| Meteorr |
Cei mai activi postatori ai saptamanii
| virgil | ||||
| Forever_Man | ||||
| Dacu2 | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Meteorr | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 29 utilizatori conectați: 1 Înregistrați, 0 Invizibil și 28 Vizitatori ilasus
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
2 participanți
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 1 din 2
Pagina 1 din 2 • 1, 2 
 Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Ceea ce se cerceteaza, ceea ce e nefinalizat si sau la care autorul nu e convins, in un cuvint un fel de cos cu gunoi.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Incerchind mai departe sa explotez Mica teorema a lui Fermat care sa ajute cu o demonstratie elementara la rezolvarea Marii teoreme a lui Fermat care sa amintim ce spune Mica teorema:
"1) Daca p este un numar prim, iar a un intreg oarecare, atunci:
)
2) Daca a nu e divizibil cu p, atunci relatia 1) se mai scrie:
) "
"
Pina la urma putem scrie asa:
 <=>
<=>
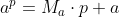
2)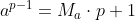 inmultind egalitatea cu a ajungem la relatia 1
inmultind egalitatea cu a ajungem la relatia 1
Scriem ecuatia fermatica asa:
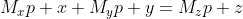
p=M_{z}p+z-&space;(x+y))
Acum fiti atenti ce spune ultima egalitate (Daca, nu am gresit cu nimic la calcule pina aici) !
Ea noua ne spune caci) strict trebue sa fie un numar divizibil cu
strict trebue sa fie un numar divizibil cu  , adica un multiplu de Incerchind mai departe sa explotez Mica teorema a lui Fermat care sa ajute cu o demonstratie elementara la rezolvarea Marii teoreme a lui Fermat care sa amintim ce spune Mica teorema:
, adica un multiplu de Incerchind mai departe sa explotez Mica teorema a lui Fermat care sa ajute cu o demonstratie elementara la rezolvarea Marii teoreme a lui Fermat care sa amintim ce spune Mica teorema:
"1) Daca p este un numar prim, iar a un intreg oarecare, atunci:
)
2) Daca a nu e divizibil cu p, atunci relatia 1) se mai scrie:
) "
"
Pina la urma putem scrie asa:
 <=>
<=>
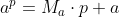
2)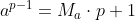 inmultind egalitatea cu a ajungem la relatia 1
inmultind egalitatea cu a ajungem la relatia 1
Scriem ecuatia fermatica asa:
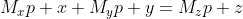
p=M_{z}p+z-&space;(x+y))
Acum fiti atenti ce spune ultima egalitate (Daca, nu am gresit cu nimic la calcule pina aici) !
Ea noua ne spune caci) strict trebue sa fie un numar divizibil cu
strict trebue sa fie un numar divizibil cu  .
.
Din regulile deduse mai demult stim caci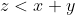 =>
=> ) este un numar negativ.
este un numar negativ.
Din alta regula dedusa mai demult stim caci daca x,y,z formeaza un triunghi, atunci valorile sumei laturilor x+y va fi cuprinsa in inervalul: (z, 2z).
Deci valoarea diferentei) este cuprinsa in intervalul
este cuprinsa in intervalul )
La fel din regulele deduse mai demult stim caci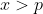 , de aici rezulta caci
, de aici rezulta caci 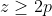
Pina la urma trebue de determinat cum este) daca este negativ si divizibil cu p.
daca este negativ si divizibil cu p.
In cazul in care se demonstreaza caci) nu este divizibil cu p , cred ca se demonstreaza definitiv teorema.
nu este divizibil cu p , cred ca se demonstreaza definitiv teorema.
Ce e interesant , este faptul ca exista o strinsa legatura dintre putere si x,y,z.
Ceea ce nu am mai gasit nicaeri.
"1) Daca p este un numar prim, iar a un intreg oarecare, atunci:
2) Daca a nu e divizibil cu p, atunci relatia 1) se mai scrie:
Pina la urma putem scrie asa:
2)
Scriem ecuatia fermatica asa:
Acum fiti atenti ce spune ultima egalitate (Daca, nu am gresit cu nimic la calcule pina aici) !
Ea noua ne spune caci
"1) Daca p este un numar prim, iar a un intreg oarecare, atunci:
2) Daca a nu e divizibil cu p, atunci relatia 1) se mai scrie:
Pina la urma putem scrie asa:
2)
Scriem ecuatia fermatica asa:
Acum fiti atenti ce spune ultima egalitate (Daca, nu am gresit cu nimic la calcule pina aici) !
Ea noua ne spune caci
Din regulile deduse mai demult stim caci
Din alta regula dedusa mai demult stim caci daca x,y,z formeaza un triunghi, atunci valorile sumei laturilor x+y va fi cuprinsa in inervalul: (z, 2z).
Deci valoarea diferentei
La fel din regulele deduse mai demult stim caci
Pina la urma trebue de determinat cum este
In cazul in care se demonstreaza caci
Ce e interesant , este faptul ca exista o strinsa legatura dintre putere si x,y,z.
Ceea ce nu am mai gasit nicaeri.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Ce sa mai demonstram ca doarca am dedus niste reguli prin care se spunea caci sunt 2 variante (defapt 4, insa din cauza ca schimbarea pozitiilor numerelor la adunare nu schimba solutia reducem la 2) de paritate a le lui x,y,z anume:
1) x- impar; y- par; z- impar.
2) x- impar; y- impar; z- par.
Daca asa, atunci avem:
1)
2)
Q.E.D.
Oare ?! Am gresit ceva pe undeva sau nu ?!
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Aaaa da, am gresit.
Chiar daca diferenta este o valoare para, nu inseamna ca ea nu e divizibila cu p, adica.... diferenta e un multiplu de p.
Ex: p=3, diferenta =6, 12, etc.
Chiar daca diferenta este o valoare para, nu inseamna ca ea nu e divizibila cu p, adica.... diferenta e un multiplu de p.
Ex: p=3, diferenta =6, 12, etc.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Observația la care ai ajuns, adică faptul că x+y-z trebuie să fie un număr divizibil cu p este corectă.
Nu știu prin care subiect am am menționat și eu acest aspect în mai multe rânduri, iar acest aspect se demonstrează într-adevăr, cel mai simplu prin mica teoremă a lui Fermat, deși se poate arăta în mai multe feluri.
Plecând de la această observație, din ce am analizat și eu, se poate arăta că una din soluțiile x, y sau z trebuie să fie o soluție divizibilă cu p pentru cazul în care n=p prim impar.
La un moment dat meteor, eu m-am întrebat, dacă pentru n=p ecuația ar avea soluții, câte ar avea ?
Ar exista vreo relație între soluțiile respective dacă ecuația ar admite mai multe soluții primitive pentru un anumit n=p?
Deși am făcut o pauză cu teorema asta, la un moment dat parcă ajunsesem la concluzia că dacă ecuația are soluții pentru un anumit n, atunci ea trebuie să aibă obligatoriu soluții și pentru z-y=1, sau z-x=1.
Așadar, ecuația s-ar reduce doar la analiza unei ecuații de forma
x^n+y^n=(y+1)^n sau x^n+y^n=(x+1)^n.
Acesta ar putea fi un caz particular al ecuației pe care l-ai putea analiza și cred că toate celelalte soluții care ar putea exista pentru un anumit n, mai mare ca 1, ar trebui să poată fi găsite plecând de la această exprimare.
Nu știu prin care subiect am am menționat și eu acest aspect în mai multe rânduri, iar acest aspect se demonstrează într-adevăr, cel mai simplu prin mica teoremă a lui Fermat, deși se poate arăta în mai multe feluri.
Plecând de la această observație, din ce am analizat și eu, se poate arăta că una din soluțiile x, y sau z trebuie să fie o soluție divizibilă cu p pentru cazul în care n=p prim impar.
La un moment dat meteor, eu m-am întrebat, dacă pentru n=p ecuația ar avea soluții, câte ar avea ?
Ar exista vreo relație între soluțiile respective dacă ecuația ar admite mai multe soluții primitive pentru un anumit n=p?
Deși am făcut o pauză cu teorema asta, la un moment dat parcă ajunsesem la concluzia că dacă ecuația are soluții pentru un anumit n, atunci ea trebuie să aibă obligatoriu soluții și pentru z-y=1, sau z-x=1.
Așadar, ecuația s-ar reduce doar la analiza unei ecuații de forma
x^n+y^n=(y+1)^n sau x^n+y^n=(x+1)^n.
Acesta ar putea fi un caz particular al ecuației pe care l-ai putea analiza și cred că toate celelalte soluții care ar putea exista pentru un anumit n, mai mare ca 1, ar trebui să poată fi găsite plecând de la această exprimare.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Nuu, de unde ai mai scos ?!curiosul a scris:
La un moment dat meteor, eu m-am întrebat, dacă pentru n=p ecuația ar avea soluții, câte ar avea ?
Ar exista vreo relație între soluțiile respective dacă ecuația ar admite mai multe soluții primitive pentru un anumit n=p?
Deși am făcut o pauză cu teorema asta, la un moment dat parcă ajunsesem la concluzia că dacă ecuația are soluții pentru un anumit n, atunci ea trebuie să aibă obligatoriu soluții și pentru z-y=1, sau z-x=1.
Așadar, ecuația s-ar reduce doar la analiza unei ecuații de forma
x^n+y^n=(y+1)^n sau x^n+y^n=(x+1)^n.
Acesta ar putea fi un caz particular al ecuației pe care l-ai putea analiza și cred că toate celelalte soluții care ar putea exista pentru un anumit n, mai mare ca 1, ar trebui să poată fi găsite plecând de la această exprimare.
1) x^n+y^n=(y+1)^n , ai 2 termeni consecutivi, ceva mi se pare ca per n>2 precis ca nu ai solutii
2) x^n+y^n=(x+1)^n e la fel ca la cazul 1), cu atit mai mult cai aici y-ul e cuprins in intervalul (x, x+1), in cazul in care ai avut in vedere ca x < y < z
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
De la faptul că, în cazul în care n este un număr prim impar p, fie z-y, fie z-x (poate chiar ambele), trebuie obligatoriu să fie numere la puterea p.meteor a scris:Nuu, de unde ai mai scos ?!
1) x^n+y^n=(y+1)^n , ai 2 termeni consecutivi, ceva mi se pare ca per n>2 precis ca nu ai solutii
2) x^n+y^n=(x+1)^n e la fel ca la cazul 1), cu atit mai mult cai aici y-ul e cuprins in intervalul (x, x+1), in cazul in care ai avut in vedere ca x < y < z
Rezultă din demonstrația lui Geza și anume faptul că din dezvoltarea
parantezele din dreapta pot avea ca unic factor comun doar p la puterea 1..
Dacă dezvolți atât
1 la puterea p este 1.
Dacă ecuația lui Fermat ar admite soluții, pentru n=p prim, atunci ea trebuie să aibă soluții și pentru cazul în care z-x sau z-y este egal cu 1, pentru că 1 este un număr la puterea p.
Deși nu sunt sigur de corectitudinea raționamentului pe care l-am analizat cândva, dacă ecuația ar avea soluții, atunci ea trebuie să admită obligatoriu și soluții pentru z-x sau z-y egal cu 1.
Oricum, dacă tot topicul se referă la cazuri particulare ale teoremei, încearcă să demonstrezi doar că
Sincer îți dau eu un premiu pentru o demonstrație corectă a cazului de mai sus, dar una dedusă de tine.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
La moment nu dau de demonstratia acestui caz, insa cred in continuare ca este ceva simplu.
Am gasit intimplator un document bunisor, de unde la o prima privire (teorema lui Serpinschi), hopa si:
Din!\equiv&space;0(modp))
Inlocuind in ecuatia Fermantica in final avem:
p=-(p-1)!)
Este evident ca cel putin unul din multipli nu este natural, deci si ecuatia inseamna ca nu are solutii in N.
Din chite am inteles cutarea teorema isi trage radacinile din Mica teorema a lui Fermat.
Prea simpla e demonstratia, ceva posibil e gresit.
S-ar putea si cu alte teoreme din adresa cutare, care la fel isi trag radacina din Mica teorema a lui Fermat in mod similar de adus teorema la demonstratie foarte simpla.
Am gasit intimplator un document bunisor, de unde la o prima privire (teorema lui Serpinschi), hopa si:
Din
Inlocuind in ecuatia Fermantica in final avem:
Este evident ca cel putin unul din multipli nu este natural, deci si ecuatia inseamna ca nu are solutii in N.
Din chite am inteles cutarea teorema isi trage radacinile din Mica teorema a lui Fermat.
Prea simpla e demonstratia, ceva posibil e gresit.
S-ar putea si cu alte teoreme din adresa cutare, care la fel isi trag radacina din Mica teorema a lui Fermat in mod similar de adus teorema la demonstratie foarte simpla.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Știi de ce crezi în continuare că e simplu ?meteor a scris:La moment nu dau de demonstratia acestui caz, insa cred in continuare ca este ceva simplu.
Pentru că teorema s-a demonstrat și știi că e o certitudine asta.
Iar atât timp cât nu poți să găsești o demonstrație corectă doar a acestui caz particular, nu poți să afirmi că este simplu de demonstrat.
Vis-a-vis de Mica teoremă a lui Fermat, poți să găsești singur o demonstrație a acestei teoreme ?
Pentru tine însuți, nu trebuie să mi-o spui mie sau nouă, pentru că dacă nu, întreabă-te :
Dacă nu pot să demonstrez o Mică teoremă, atunci voi putea oare demonstra o Mare teoremă ?
Întrebarea asta mi-am ridicat-o și eu.
E un drum lung, câteodată imposibil, de la vis la realitate.
Înclin să fiu de acord cu marii matematicieni.
Pentru această teoremă nu poate exista o demonstrație elementară.
Și dacă afirm asta, ține cont că eu nu renunț ușor la ceva ce-mi pun în minte.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Cred că e corect, mai mult derivă și din teorema lui Wilson, dar trebuie menționat că a nu este divizibil cu p.
Din teorema lui Wilson avem
Din Mica teoremă a lui Fermat avem
Din cele două congruențe rezultă evident că
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
De fapt nici n-am fost suficient de atent.
De unde l-ai scos pe p factor în egalitatea
p-1 factorial se anulează o dată trecând multiplul lui z în stânga, iar în dreapta va rămâne doar factorialul lui p-1, cu semnul minus, trecându-l în dreapta.
p n-are ce căuta ca și factor lângă paranteza din stânga.
Nu-i așa ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Avem: !\equiv&space;0(modp))
Adica la impartirea prin p noua ne da un numar intreg (prin care il vom nota Ma, adica un oarecare multiplu [numar natural] dependent de a).
!}{p}=M_{a})
Extragem doar pe a^p:
!)
In locuind a cu x apoi cu y apoi cu z in ecuatia fermantica vom avea:
!+M_{y}p-(p-1)!=M_{z}p-(p-1)!)
Deoarece multiplii cei [numerele cele naturale] dependente de x,y,z sunt numere naturale (conform ipotezei) si deoarece au factor comun, atunci ii scoatem in fata, doua (p-1)! se reduc, vom avea:
p=(p-1)!)
Inainte de toate acestea am spus doar caci:
x+y>z
Nu is convins la moment, insa din formula:
!}{p}=M_{a})
inlocuind in loc de a pe x,y,z ii aflam pe
O presupunere ar fi caci mai mic ca zero.
mai mic ca zero.
INSA NU are nici o importanta cum este acest numar fata de 0, la fel ( ce e drept putin ieri am gresit semnul) nici semnul lui!) care sta in partea dreapta din egalitate nu joaca absolut nici un rol important.
care sta in partea dreapta din egalitate nu joaca absolut nici un rol important.
Daca azi corectez semnul cela, demonstratia va ramine in continuare valida.
Acum, stim bine cum am mai spus caci Mx, My, Mz sunt numere naturale, deci si suma, diferenta dintre ele la fel trebue sa dea un numar intreg.
Pentru claritate eu recomand ca aceaa suma si diferenta a multiplilor sa o notam cu un numar care apartine lui Z, care il vom boteza "multiplu dependent de multiplii Mx+My-Mz" ca aici:

!)
Deci:
!}{M_{x+y-z}})
Acum se pune intrebarea poate fi asa un numar prim p ?!
}{M_{x+y-z}}) ?!
?!
Stim doar ca un numar prim are doar 2 divizori.
Daca la aceasta impartire multiplul ar reduce toti termenii de la numarator, atunci am avea caci numarul prim e rational, sau egal cu 1, ceea ce e absurd.
ar reduce toti termenii de la numarator, atunci am avea caci numarul prim e rational, sau egal cu 1, ceea ce e absurd.
Daca multiplul ar reduce un anumit numar de factori din acel produs, insa lasind 1 factor, atunci am avea caci numarul nostru prim este egal cu un numar mai mic ca un numar pina la p-1, ceea ce e la fel absurd.
ar reduce un anumit numar de factori din acel produs, insa lasind 1 factor, atunci am avea caci numarul nostru prim este egal cu un numar mai mic ca un numar pina la p-1, ceea ce e la fel absurd.
Daca multiplul ar reduce factorii acelui produs lasind cel putin 2 factori, atunci am afla caci numarul nostru prim are mai mult de 2 divizori.
ar reduce factorii acelui produs lasind cel putin 2 factori, atunci am afla caci numarul nostru prim are mai mult de 2 divizori.
Daca nu se reduce fractia (impartirea numitorului cu numaratorul nu da un numar intreg), atunci aflam caci numarul nostru prim este un numar rational, ceea ce este la fel absurd.
Cam atit.
Era si logic Fermat sa demonstreze cazul n=4 , deoarece doar acest caz mai trebue verificat odata ce se demonstreaza cazul chind n este numar prim.
Privitor la aceea caci a nu e divizibil cu p (de mentionat caci cum am dedus mai demult a>p), se pare ca este asa, aceasta face ca si demonstrtia acesta sa ramina incopleta.
Odata ce se demonstreaza caci numerele x,y,z trebue sa fie prime cu p, cum am mai spus indata se demonstreaza complet teorema.
Stim doar una ca cel putin unul din termeni e par, deci prim cu p, despre restul cei doi, doar banueli.
(sper ca pina aici nu am facut greseli)
Adica la impartirea prin p noua ne da un numar intreg (prin care il vom nota Ma, adica un oarecare multiplu [numar natural] dependent de a).
Extragem doar pe a^p:
In locuind a cu x apoi cu y apoi cu z in ecuatia fermantica vom avea:
Deoarece multiplii cei [numerele cele naturale] dependente de x,y,z sunt numere naturale (conform ipotezei) si deoarece au factor comun, atunci ii scoatem in fata, doua (p-1)! se reduc, vom avea:
Inainte de toate acestea am spus doar caci:
x+y>z
Nu is convins la moment, insa din formula:
inlocuind in loc de a pe x,y,z ii aflam pe
O presupunere ar fi caci
INSA NU are nici o importanta cum este acest numar fata de 0, la fel ( ce e drept putin ieri am gresit semnul) nici semnul lui
Daca azi corectez semnul cela, demonstratia va ramine in continuare valida.
Acum, stim bine cum am mai spus caci Mx, My, Mz sunt numere naturale, deci si suma, diferenta dintre ele la fel trebue sa dea un numar intreg.
Pentru claritate eu recomand ca aceaa suma si diferenta a multiplilor sa o notam cu un numar care apartine lui Z, care il vom boteza "multiplu dependent de multiplii Mx+My-Mz" ca aici:
Deci:
Acum se pune intrebarea poate fi asa un numar prim p ?!
Stim doar ca un numar prim are doar 2 divizori.
Daca la aceasta impartire multiplul
Daca multiplul
Daca multiplul
Daca nu se reduce fractia (impartirea numitorului cu numaratorul nu da un numar intreg), atunci aflam caci numarul nostru prim este un numar rational, ceea ce este la fel absurd.
Cam atit.
Era si logic Fermat sa demonstreze cazul n=4 , deoarece doar acest caz mai trebue verificat odata ce se demonstreaza cazul chind n este numar prim.
Privitor la aceea caci a nu e divizibil cu p (de mentionat caci cum am dedus mai demult a>p), se pare ca este asa, aceasta face ca si demonstrtia acesta sa ramina incopleta.
Odata ce se demonstreaza caci numerele x,y,z trebue sa fie prime cu p, cum am mai spus indata se demonstreaza complet teorema.
Stim doar una ca cel putin unul din termeni e par, deci prim cu p, despre restul cei doi, doar banueli.
(sper ca pina aici nu am facut greseli)
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Ar fi bine daca ar mai trece Orakle ... pe aici sa isi expuna si el parerea.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Se pare ca metoda aceasta ar fi sortata din radacina sa nu poata demonstra (complet) teorema [repet mi se pare, ipoteza vine de la aceea caci in asa caz noi am demonstra ca cel putin una din solutii ar fi rationala, INSA ecuatia fermantica spune caci daca ecuatia nu are solutii in N pentru un anumit caz, atunci aceasta solutie este irationala]
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
sau, nu?! parca pina la urma totu e ok, nu e nici o cearta intre num rationale cu irationale
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Într-adevăr meteor, este corectă relația la care ai ajuns aici și ar demonstra direct teorema lui Fermat analizând egalitatea la care ai ajuns prin teorema fundamentală a algebrei.
Din ultima egalitate, membrul din stânga se divide cu p, în timp ce membrul din dreapta nu se mai divide.
(p-1)! nu se divide cu p, ci cu orice număr prim mai mic ca p.
Așadar, egalitatea este imposibilă.
Teorema ar fi direct demonstrată.
Dar se pare că am fost neatenți amândoi.
Nu știu unde ai citit că :
dar se pare că e greșit.
Congruența corectă este
și nu
Rezultă din teorema lui Wilson :
și mica teoremă a lui Fermat (corectă, nu greșită ca în mesajul anterior) :
Din cele două congruențe rezultă că
Prin urmare, aceasta invalidează corectitudinea demonstrației pe care ai dezvoltat-o.
Dacă încerci în mod identic cu relația de mai sus, problema devine cazul n=p-1.
O să analizez și ce ai mai scris în continuare să văd ce putem folosi de acolo.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Teorema fundamentală a aritmeticii am vrut să spun, cea despre unicitatea factorizării.curiosul a scris:
Într-adevăr meteor, este corectă relația la care ai ajuns aici și ar demonstra direct teorema lui Fermat analizând egalitatea la care ai ajuns prin teorema fundamentală a algebrei.
Din ultima egalitate, membrul din stânga se divide cu p, în timp ce membrul din dreapta nu se mai divide.
(p-1)! nu se divide cu p, ci cu orice număr prim mai mic ca p.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
La fel de bine rezultă și căcuriosul a scris:...din teorema lui Wilson :,
și mica teoremă a lui Fermat (corectă, nu greșită ca în mesajul anterior) :
Din cele două congruențe rezultă că, generalizat pentru orice a nedivizibil cu p prim.
Dar tot nu te-ajută să demonstrezi cazul n=p.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
http://fs.gallup.unm.edu/AUNFITN.pdf pag. 14 Teorema lui Serpinschi.
Defapt, odata ce se demonstreaza caci doar pentru: n=p (prim); (x,y,z)=1; (x,p)=1 ; (y,p)=1; (z,p)=1 trebue analizaindata, se demonstreaza pentru toate cazurile n>2.
Nici nu mai este nevoe de demonstrat cazul n=4 (numar neprim, urmat dupa un numar prim par care pentru cazul dat (n=2) are solutii), deoarece din o demonstratie mai anterioara am gasit doar o metoda de demonstrare (cu conditia ca se respecta cerintele ca de mai sus) pentru cazurile n=p-1 (in cazul p=5, avem cazul p=5-1=4)
Defapt, odata ce se demonstreaza caci doar pentru: n=p (prim); (x,y,z)=1; (x,p)=1 ; (y,p)=1; (z,p)=1 trebue analizaindata, se demonstreaza pentru toate cazurile n>2.
Nici nu mai este nevoe de demonstrat cazul n=4 (numar neprim, urmat dupa un numar prim par care pentru cazul dat (n=2) are solutii), deoarece din o demonstratie mai anterioara am gasit doar o metoda de demonstrare (cu conditia ca se respecta cerintele ca de mai sus) pentru cazurile n=p-1 (in cazul p=5, avem cazul p=5-1=4)
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
O demonstrație completă a teoremei impune obligatoriu și demonstrarea cazului n=4.
Cu excepția lui 2, toate celelalte numere prime sunt impare.
Dacă se demonstrează cazul n=p prim impar, atunci orice număr care nu este o putere de doi, are în factorizarea lui cel puțin un număr prim impar, iar ecuația poate fi adusă la un exponent prim impar.
Dar cum rămâne cu cazul în care n este o putere de 2 ?
În această situație, ecuația nu poate fi adusă la un exponent număr prim impar.
Iar pentru n=2 ecuația are soluții.
Carevasăzică, dacă se demonstrează și cazul n=4, atunci ecuația pentru exponent putere de 2, mai mare ca 4, poate fi scrisă ca o ecuație cu exponentul 4 :

^4+\left&space;(y^{2^{n-2}}&space;\right&space;)^4=\left&space;(z^{2^{n-2}}&space;\right&space;)^4)
Deci este absolut necesar demonstrarea cazului n=4 pentru o demonstrație completă a teoremei.
Nu m-am uitat pe pdf-ul ăla.
Mă uit acum.
Cu excepția lui 2, toate celelalte numere prime sunt impare.
Dacă se demonstrează cazul n=p prim impar, atunci orice număr care nu este o putere de doi, are în factorizarea lui cel puțin un număr prim impar, iar ecuația poate fi adusă la un exponent prim impar.
Dar cum rămâne cu cazul în care n este o putere de 2 ?
În această situație, ecuația nu poate fi adusă la un exponent număr prim impar.
Iar pentru n=2 ecuația are soluții.
Carevasăzică, dacă se demonstrează și cazul n=4, atunci ecuația pentru exponent putere de 2, mai mare ca 4, poate fi scrisă ca o ecuație cu exponentul 4 :
Deci este absolut necesar demonstrarea cazului n=4 pentru o demonstrație completă a teoremei.
Nu m-am uitat pe pdf-ul ăla.
Mă uit acum.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Într-adevăr la teorema 1.2.11 a lui Sierpinski, așa cum ai menționat-o și tu, este o greșeală. Cel mai probabil de redactare.
Congruența corectă este
!\equiv&space;0(modp))
Iar asta se demonstrează ușor.
Mai mult, dacă ar fi adevărată congruența!\equiv&space;0(modp)) ,
,
a nu poate fi divizibil cu p, iată cel puțin un contraexemplu :
)
În schimb, congruența!\equiv&space;0(modp)) verifică orice a nedivizibil cu p.
verifică orice a nedivizibil cu p.
Documentul este bun de pus la arhivă totuși.
O să-l citesc complet.
Congruența corectă este
Iar asta se demonstrează ușor.
Mai mult, dacă ar fi adevărată congruența
a nu poate fi divizibil cu p, iată cel puțin un contraexemplu :
În schimb, congruența
Documentul este bun de pus la arhivă totuși.
O să-l citesc complet.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Curiosul carevasăzică ( ), eu asa am zis:
), eu asa am zis:
1. Daca ai demonstratia per caz 2 si aici sunt solutii, atunci ai de verificat per caz 4.
2. Avem demonstratii pentru casurile n=p prim si n= p-1 (pentru anumite conditii).
3. Pentru cazurile p >2, fie ca le avem.
4. Ne ramine deci cel putin cazul n=4 de verificat, INSA din n=p-1, aflam caci cu metoda de rezolvare n= p-1 demonstram si cazul n=4.
5. Toata problema se rezuma la aceea ca x,y,z sa fie toate 3 simultan fiecare prime cu p, adica nemultipli de p, daca se demonstreaza ca asa este, atunci se rezolva complet problema.
6. Demonstratia prin metoda n= p-1 a cazului n=2 tot merge bine, repet nu trebue de uitat ca avem niste conditii.
Daca sa respectam acele conditii, intradevar nu avem solutii, deoarece din formula pitagorenilor rezulta caci unul din termeni este par (multiplu de 2), care deci este divizibil cu 2, deci in asa cazuri nu avem de aface.
1. Daca ai demonstratia per caz 2 si aici sunt solutii, atunci ai de verificat per caz 4.
2. Avem demonstratii pentru casurile n=p prim si n= p-1 (pentru anumite conditii).
3. Pentru cazurile p >2, fie ca le avem.
4. Ne ramine deci cel putin cazul n=4 de verificat, INSA din n=p-1, aflam caci cu metoda de rezolvare n= p-1 demonstram si cazul n=4.
5. Toata problema se rezuma la aceea ca x,y,z sa fie toate 3 simultan fiecare prime cu p, adica nemultipli de p, daca se demonstreaza ca asa este, atunci se rezolva complet problema.
6. Demonstratia prin metoda n= p-1 a cazului n=2 tot merge bine, repet nu trebue de uitat ca avem niste conditii.
Daca sa respectam acele conditii, intradevar nu avem solutii, deoarece din formula pitagorenilor rezulta caci unul din termeni este par (multiplu de 2), care deci este divizibil cu 2, deci in asa cazuri nu avem de aface.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Ok, cred că încep să înțeleg ce vrei să spui (te exprimi cam greoi sau incomplet)
Dacă ei cazurile n=p și n=p-1, într-adevăr, este suficient.
Ca să ajungi să generalizezi condiția pentru ambele cazuri, adică (x, y, z, p)=1, trebuie să o arăți și pentru cazul n=p.
Deocamdată, rezultă evident că în cazul n=p-1, așa cum ai arătat, una din soluții trebuie să fie divizibilă cu p, iar dacă demonstrezi că (x, y, z, p) sunt prime între ele, ai demonstrat cazul n=p-1.
Dar mai trebuie să arăți și pentru cazul n=p că una din soluții se divide obligatoriu cu p ca să poți generaliza condiția ce ar trebui îndeplinită ca să demonstreze teorema, anume (x, y, z, p)=1.
Pentru p=3 se poate arăta ușor, dar pentru celelalte numere prime e ceva mai complicat.
Dacă ei cazurile n=p și n=p-1, într-adevăr, este suficient.
Ca să ajungi să generalizezi condiția pentru ambele cazuri, adică (x, y, z, p)=1, trebuie să o arăți și pentru cazul n=p.
Deocamdată, rezultă evident că în cazul n=p-1, așa cum ai arătat, una din soluții trebuie să fie divizibilă cu p, iar dacă demonstrezi că (x, y, z, p) sunt prime între ele, ai demonstrat cazul n=p-1.
Dar mai trebuie să arăți și pentru cazul n=p că una din soluții se divide obligatoriu cu p ca să poți generaliza condiția ce ar trebui îndeplinită ca să demonstreze teorema, anume (x, y, z, p)=1.
Pentru p=3 se poate arăta ușor, dar pentru celelalte numere prime e ceva mai complicat.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Nu incurca!curiosul a scris:Ok, cred că încep să înțeleg ce vrei să spui (te exprimi cam greoi sau incomplet)
Dacă ei cazurile n=p și n=p-1, într-adevăr, este suficient.
Ca să ajungi să generalizezi condiția pentru ambele cazuri, adică (x, y, z, p)=1, trebuie să o arăți și pentru cazul n=p.
Deocamdată, rezultă evident că în cazul n=p-1, așa cum ai arătat, una din soluții trebuie să fie divizibilă cu p, iar dacă demonstrezi că (x, y, z, p) sunt prime între ele, ai demonstrat cazul n=p-1.
Dar mai trebuie să arăți și pentru cazul n=p că una din soluții se divide obligatoriu cu p ca să poți generaliza condiția ce ar trebui îndeplinită ca să demonstreze teorema, anume (x, y, z, p)=1.
Pentru p=3 se poate arăta ușor, dar pentru celelalte numere prime e ceva mai complicat.
Sistemul:
(x,p)=1
(y,p)=1
(z,p)=1
(x,y,z)=1
Ex:
p=3,x=4,y=5,z=7.
Nu este una si aceeasi cu expresia:
(x,y,z,p)=1
Ex:
p= 3, x= 3*4, y=4, z=5
Cred ca e bine sa lasam creerii sa se odihneasca pe o bucata de timp , alt fel

meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Sigur, ai dreptate.meteor a scris:
Nu incurca!
Sistemul:
(x,p)=1
(y,p)=1
(z,p)=1
(x,y,z)=1
Ex:
p=3,x=4,y=5,z=7.
Nu este una si aceeasi cu expresia:
(x,y,z,p)=1
Eram sigur că ai să înțelegi ce vreau să spun, deși am sărit peste menționarea faptului că x, y, z, p trebuie să fie prime între ele două câte două.
Dacă am timp astăzi am să-ți arăt cum cred că se demonstrează generalizat, pentru n=p, faptul că una din soluții trebuie obligatoriu să se dividă cu p, dacă x, y, z sunt soluții ale ecuației.
Așa cum ai spus, ar trebui după aia să demonstrăm că niciuna nu poate să se dividă cu p pentru a demonstra teorema.
Dar e mai dificil.
Poate mai dai de vreun document bunișor de unde să mai culegem ceva interesant și folositor.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
De chite ori am spus: "Omul informat este puternic " ?!
Ideea este, ca dechit sa stai sa buchii si nimic sa nu obtii, mai bine cel putin inveti toate teoremele cunoscute in ziua de azi.
Daca vrei sa faci un pas si mai mare, atunci sa le intelegi cum s-au obtinut (demonstrat).
Spre exemplu eu nu stiam de Teorema numerelor prime, indata cum am aflat de ea, multe cai si-au deschis drumul.
La aceasta teorema au lucrat zeci de oameni mari.
Daca as fi stiut si inteles toate teoremele din ziua de azi din matematica, cred ca eram sa descoper inca jumatate de matematica, dar, greu merge cu invatatul
Ar fi bine sa se deschida o lista cu teoreme din un anumit domeniu (fie teoria numerelor), inafara de deoreme expuse chit mai clar nimic in acel subiect sa nu fie.
Ideea este, ca dechit sa stai sa buchii si nimic sa nu obtii, mai bine cel putin inveti toate teoremele cunoscute in ziua de azi.
Daca vrei sa faci un pas si mai mare, atunci sa le intelegi cum s-au obtinut (demonstrat).
Spre exemplu eu nu stiam de Teorema numerelor prime, indata cum am aflat de ea, multe cai si-au deschis drumul.
La aceasta teorema au lucrat zeci de oameni mari.
Daca as fi stiut si inteles toate teoremele din ziua de azi din matematica, cred ca eram sa descoper inca jumatate de matematica, dar, greu merge cu invatatul
Ar fi bine sa se deschida o lista cu teoreme din un anumit domeniu (fie teoria numerelor), inafara de deoreme expuse chit mai clar nimic in acel subiect sa nu fie.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
per curiosul:
Gresela e in aceea caci am spus ca cel putin unul din termeni este numar par, deci si nedivizibil cu p. Am spus tot eu mai sus ca daca un numar este par, nu inseamna ca nu e divizibil cu un numar prim impar. Altfel spus valoarea acestui numar par poate fi egala cu 2 inmultit cu un oarecare multiplu de p.
Aceasta pina aici inseamna ca nu avem nici o dovada certa ca cel putin unul din termeni e diferit de p, si aceasta ne arunca cu un pas in urma.
Avem insa alt drum, stim caci e necesar ca=1) (si aceasta nu in zadar s-a facut, deoarece descrie solutia minima, daca ea este atunci mai exista o multime de solutii, daca nu am pune aceasta relatie, am cobori vesnic prin scoterea factorului comun).
(si aceasta nu in zadar s-a facut, deoarece descrie solutia minima, daca ea este atunci mai exista o multime de solutii, daca nu am pune aceasta relatie, am cobori vesnic prin scoterea factorului comun).
Din relatia=1) rezulta ca cel putin unul din
rezulta ca cel putin unul din 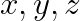 nu este divizibil cu p.
nu este divizibil cu p.
1. Fie caci acest termen este x, iar restul ar fi divizibili cu p.
Vom avea: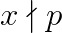 ;
; 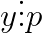 ;
; 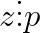
Ecuatia fermantica se mai poate scrie:
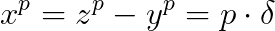
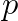 este factorul comun dintre y,z.
este factorul comun dintre y,z.
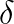 este restul produsul care ramine.
este restul produsul care ramine.
Din egalitatea de mai sus ajungem la concluzia caci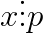 , insa din regula dedusa mai sus stim bine caci aceasta este absurd.
, insa din regula dedusa mai sus stim bine caci aceasta este absurd.
La fel se deduce si pentru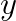 si pentru
si pentru 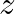 .
.
Concluzia este : Cel putin doi termeni din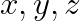 nu sunt divizibili cu p.
nu sunt divizibili cu p.
Pina aici ajungem la un rezultat care confirma teorema la un numar foarte foarte mare de cazuri, la figurat spus cam 70% din teorema e demonstrat.
Mai departe nu is prea convins la moment.
Fie unul din termeni este divizibil cu p, iar ceilalti asa cum am demonstrat nu este divizibil cu p.
Adica: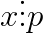 ;
; 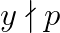 ;
; 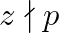
Scriem ecuatia fermantica:
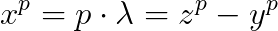
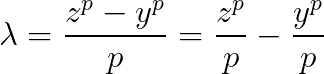
Aceasta spune ca in asa caz atit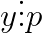 chit si
chit si 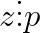 , ceea ce este o absurtitate, reesind din regulile deduse mai sus.
, ceea ce este o absurtitate, reesind din regulile deduse mai sus.
La fel se deduce si pentru y si pentru z.
Sa fie oare Q.E.D. ?!
Gresela e in aceea caci am spus ca cel putin unul din termeni este numar par, deci si nedivizibil cu p. Am spus tot eu mai sus ca daca un numar este par, nu inseamna ca nu e divizibil cu un numar prim impar. Altfel spus valoarea acestui numar par poate fi egala cu 2 inmultit cu un oarecare multiplu de p.
Aceasta pina aici inseamna ca nu avem nici o dovada certa ca cel putin unul din termeni e diferit de p, si aceasta ne arunca cu un pas in urma.
Avem insa alt drum, stim caci e necesar ca
Din relatia
1. Fie caci acest termen este x, iar restul ar fi divizibili cu p.
Vom avea:
Ecuatia fermantica se mai poate scrie:
Din egalitatea de mai sus ajungem la concluzia caci
La fel se deduce si pentru
Concluzia este : Cel putin doi termeni din
Pina aici ajungem la un rezultat care confirma teorema la un numar foarte foarte mare de cazuri, la figurat spus cam 70% din teorema e demonstrat.
Mai departe nu is prea convins la moment.
Fie unul din termeni este divizibil cu p, iar ceilalti asa cum am demonstrat nu este divizibil cu p.
Adica:
Scriem ecuatia fermantica:
Aceasta spune ca in asa caz atit
La fel se deduce si pentru y si pentru z.
Sa fie oare Q.E.D. ?!
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
Pagina 1 din 2 • 1, 2 
 Subiecte similare
Subiecte similare» Demonstrațiile cazurilor particulare ale Marii teoreme a lui Fermat
» Demonstrația algebrică a marii teoreme a lui Fermat
» Cercetari asupra fenomenelor de qualia
» Demonstrația algebrică a marii teoreme a lui Fermat
» Cercetari asupra fenomenelor de qualia
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 1 din 2
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 