Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Meteorr Ieri la 21:34
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Joi 21 Noi 2024, 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la No_name în How Self-Reference Builds the World - articol nou
( 1 )
» Mesaj de la CAdi în Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
( 1 )
» Mesaj de la No_name în Ce anume "generează" legile fizice?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Dacu2 | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Abel Cavaşi |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| virgil | ||||
| Dacu2 | ||||
| CAdi | ||||
| Meteorr | ||||
| ilasus | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 47 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 47 Vizitatori :: 2 Motoare de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
2 participanți
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 2 din 2
Pagina 2 din 2 •  1, 2
1, 2
 Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Rezumarea primului mesaj :
Ceea ce se cerceteaza, ceea ce e nefinalizat si sau la care autorul nu e convins, in un cuvint un fel de cos cu gunoi.
Ceea ce se cerceteaza, ceea ce e nefinalizat si sau la care autorul nu e convins, in un cuvint un fel de cos cu gunoi.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
De chite ori am spus: "Omul informat este puternic " ?!
Ideea este, ca dechit sa stai sa buchii si nimic sa nu obtii, mai bine cel putin inveti toate teoremele cunoscute in ziua de azi.
Daca vrei sa faci un pas si mai mare, atunci sa le intelegi cum s-au obtinut (demonstrat).
Spre exemplu eu nu stiam de Teorema numerelor prime, indata cum am aflat de ea, multe cai si-au deschis drumul.
La aceasta teorema au lucrat zeci de oameni mari.
Daca as fi stiut si inteles toate teoremele din ziua de azi din matematica, cred ca eram sa descoper inca jumatate de matematica, dar, greu merge cu invatatul
Ar fi bine sa se deschida o lista cu teoreme din un anumit domeniu (fie teoria numerelor), inafara de deoreme expuse chit mai clar nimic in acel subiect sa nu fie.
Ideea este, ca dechit sa stai sa buchii si nimic sa nu obtii, mai bine cel putin inveti toate teoremele cunoscute in ziua de azi.
Daca vrei sa faci un pas si mai mare, atunci sa le intelegi cum s-au obtinut (demonstrat).
Spre exemplu eu nu stiam de Teorema numerelor prime, indata cum am aflat de ea, multe cai si-au deschis drumul.
La aceasta teorema au lucrat zeci de oameni mari.
Daca as fi stiut si inteles toate teoremele din ziua de azi din matematica, cred ca eram sa descoper inca jumatate de matematica, dar, greu merge cu invatatul
Ar fi bine sa se deschida o lista cu teoreme din un anumit domeniu (fie teoria numerelor), inafara de deoreme expuse chit mai clar nimic in acel subiect sa nu fie.
meteor- Foarte activ

- Numarul mesajelor : 2203
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
per curiosul:
Gresela e in aceea caci am spus ca cel putin unul din termeni este numar par, deci si nedivizibil cu p. Am spus tot eu mai sus ca daca un numar este par, nu inseamna ca nu e divizibil cu un numar prim impar. Altfel spus valoarea acestui numar par poate fi egala cu 2 inmultit cu un oarecare multiplu de p.
Aceasta pina aici inseamna ca nu avem nici o dovada certa ca cel putin unul din termeni e diferit de p, si aceasta ne arunca cu un pas in urma.
Avem insa alt drum, stim caci e necesar ca=1) (si aceasta nu in zadar s-a facut, deoarece descrie solutia minima, daca ea este atunci mai exista o multime de solutii, daca nu am pune aceasta relatie, am cobori vesnic prin scoterea factorului comun).
(si aceasta nu in zadar s-a facut, deoarece descrie solutia minima, daca ea este atunci mai exista o multime de solutii, daca nu am pune aceasta relatie, am cobori vesnic prin scoterea factorului comun).
Din relatia=1) rezulta ca cel putin unul din
rezulta ca cel putin unul din 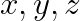 nu este divizibil cu p.
nu este divizibil cu p.
1. Fie caci acest termen este x, iar restul ar fi divizibili cu p.
Vom avea: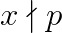 ;
; 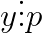 ;
; 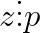
Ecuatia fermantica se mai poate scrie:
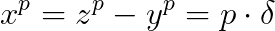
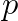 este factorul comun dintre y,z.
este factorul comun dintre y,z.
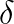 este restul produsul care ramine.
este restul produsul care ramine.
Din egalitatea de mai sus ajungem la concluzia caci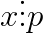 , insa din regula dedusa mai sus stim bine caci aceasta este absurd.
, insa din regula dedusa mai sus stim bine caci aceasta este absurd.
La fel se deduce si pentru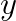 si pentru
si pentru 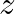 .
.
Concluzia este : Cel putin doi termeni din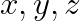 nu sunt divizibili cu p.
nu sunt divizibili cu p.
Pina aici ajungem la un rezultat care confirma teorema la un numar foarte foarte mare de cazuri, la figurat spus cam 70% din teorema e demonstrat.
Mai departe nu is prea convins la moment.
Fie unul din termeni este divizibil cu p, iar ceilalti asa cum am demonstrat nu este divizibil cu p.
Adica: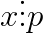 ;
; 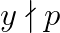 ;
; 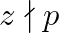
Scriem ecuatia fermantica:
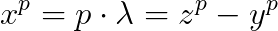
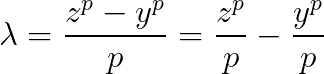
Aceasta spune ca in asa caz atit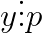 chit si
chit si 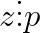 , ceea ce este o absurtitate, reesind din regulile deduse mai sus.
, ceea ce este o absurtitate, reesind din regulile deduse mai sus.
La fel se deduce si pentru y si pentru z.
Sa fie oare Q.E.D. ?!
Gresela e in aceea caci am spus ca cel putin unul din termeni este numar par, deci si nedivizibil cu p. Am spus tot eu mai sus ca daca un numar este par, nu inseamna ca nu e divizibil cu un numar prim impar. Altfel spus valoarea acestui numar par poate fi egala cu 2 inmultit cu un oarecare multiplu de p.
Aceasta pina aici inseamna ca nu avem nici o dovada certa ca cel putin unul din termeni e diferit de p, si aceasta ne arunca cu un pas in urma.
Avem insa alt drum, stim caci e necesar ca
Din relatia
1. Fie caci acest termen este x, iar restul ar fi divizibili cu p.
Vom avea:
Ecuatia fermantica se mai poate scrie:
Din egalitatea de mai sus ajungem la concluzia caci
La fel se deduce si pentru
Concluzia este : Cel putin doi termeni din
Pina aici ajungem la un rezultat care confirma teorema la un numar foarte foarte mare de cazuri, la figurat spus cam 70% din teorema e demonstrat.
Mai departe nu is prea convins la moment.
Fie unul din termeni este divizibil cu p, iar ceilalti asa cum am demonstrat nu este divizibil cu p.
Adica:
Scriem ecuatia fermantica:
Aceasta spune ca in asa caz atit
La fel se deduce si pentru y si pentru z.
Sa fie oare Q.E.D. ?!
meteor- Foarte activ

- Numarul mesajelor : 2203
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Din păcate nu, meteor și chiar mă întreb cum de nu vezi greșeli simple.
Dar dacă tot vrei părerea mea nu vreau să te critic, ci o să-ți răspund cât pot de clar.
Să le luăm la rând.
M-am gândit că poate ai fost doar prea entuziasmat și într-un final îți dai seama singur, așa cum ai și făcut de altfel.
Presupunând că două dintre ele se divid cu p, acesta poate fi scos factor comun prin separarea soluțiilor divizibile cu p de aceeași parte a egalității și ar rezulta că și cealaltă soluție trebuie să-l conțină pe p factor.
Imposibil prin condiția pe care trebuie să o îndeplinească soluțiile ecuației, pentru că ecuația admite înainte de toate soluții primitive x, y, z.
Sper să înțelegi fără să mai scriu ecuații, deși am explicat asta de cinșpe mii de ori, aproape de fiecare dată când credeam că o anumită demonstrație a teoremei pe care o găsisem este corectă.
Pentru că chiar dacă membrul stânga este întreg pozitiv, natural, chiar dacă y și z nu sunt divizibile cu p, fracțiile respective sunt numere raționale, iar suma celor două numere raționale ce constituie membrul din dreapta poate fi natural.
Exemple poți găsi chiar tu însuți.
Gândește-te că dacă logica raționamentului tău ar fi corectă, iar oricare două din x, y, z nu pot avea niciun factor comun, ecuația ar putea fi simplu scrisă :
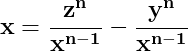
Atât z, cât și y nu sunt divizibile cu x, iar logica ar fi aceeași cu cea a ecuației tale, situație în care teorema ar fi demult demonstrată, datorită simplității demonstrației.
Ca să-ți explic și altfel, demonstrația ta este valabilă și pentru cazul n=2, pentru că în acest caz n=2, una din soluții este obligatoriu pară, ceea ce ar însemna că și pentru cazul n=2 ecuația nu are soluții.
Dar pentru cazul n=2 ecuația are soluții.
Deci, ce zici este corectă ?
Dar dacă tot vrei părerea mea nu vreau să te critic, ci o să-ți răspund cât pot de clar.
Să le luăm la rând.
Este evident și de aceea nici nu am comentat această concluzie.meteor a scris:Gresela e in aceea caci am spus ca cel putin unul din termeni este numar par, deci si nedivizibil cu p. Am spus tot eu mai sus ca daca un numar este par, nu inseamna ca nu e divizibil cu un numar prim impar. Altfel spus valoarea acestui numar par poate fi egala cu 2 inmultit cu un oarecare multiplu de p.
M-am gândit că poate ai fost doar prea entuziasmat și într-un final îți dai seama singur, așa cum ai și făcut de altfel.
Dacă x, y și z sunt toate prime între ele, mai exact oricare două nu au un divizor comun mai mare ca unitatea, atunci cel puțin două nu se divid cu p, concluzie la care ai ajuns și tu.
Presupunând că două dintre ele se divid cu p, acesta poate fi scos factor comun prin separarea soluțiilor divizibile cu p de aceeași parte a egalității și ar rezulta că și cealaltă soluție trebuie să-l conțină pe p factor.
Imposibil prin condiția pe care trebuie să o îndeplinească soluțiile ecuației, pentru că ecuația admite înainte de toate soluții primitive x, y, z.
Sper să înțelegi fără să mai scriu ecuații, deși am explicat asta de cinșpe mii de ori, aproape de fiecare dată când credeam că o anumită demonstrație a teoremei pe care o găsisem este corectă.
Din păcate nu, meteor.
Pentru că chiar dacă membrul stânga este întreg pozitiv, natural, chiar dacă y și z nu sunt divizibile cu p, fracțiile respective sunt numere raționale, iar suma celor două numere raționale ce constituie membrul din dreapta poate fi natural.
Exemple poți găsi chiar tu însuți.
Gândește-te că dacă logica raționamentului tău ar fi corectă, iar oricare două din x, y, z nu pot avea niciun factor comun, ecuația ar putea fi simplu scrisă :
Atât z, cât și y nu sunt divizibile cu x, iar logica ar fi aceeași cu cea a ecuației tale, situație în care teorema ar fi demult demonstrată, datorită simplității demonstrației.
Ca să-ți explic și altfel, demonstrația ta este valabilă și pentru cazul n=2, pentru că în acest caz n=2, una din soluții este obligatoriu pară, ceea ce ar însemna că și pentru cazul n=2 ecuația nu are soluții.
Dar pentru cazul n=2 ecuația are soluții.
Deci, ce zici este corectă ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Regula caci cel putin doi termeni nu sunt divizibili (multipli de p) cu p, ramine in picioare.
Ramine de demonstrat (aflat) daca la fel este cu toti trei termeni.
La cazul n=2, nu este aceeasi poveste ?! Oare nu daca (x,y,z)=1, atunci cel putin 2 factori nu sunt divizibili cu 2 (am dedus doar ca unul e par celelalte doi factori impari).
Despre faptul caci exista solutii solutii per n=2, posibil aceeasi poveste sa fie si per n>2, eu nus'
De luat in seama ca 2 e numar prim DAR par, asa proprietate restul numerelor prime nu au, si cred ca e bine de luat in seama caci per puterea 2 suma a doi termeni patrati nu se poate discompune in produs.
Pina ce ramine de sapat.
Ramine de demonstrat (aflat) daca la fel este cu toti trei termeni.
La cazul n=2, nu este aceeasi poveste ?! Oare nu daca (x,y,z)=1, atunci cel putin 2 factori nu sunt divizibili cu 2 (am dedus doar ca unul e par celelalte doi factori impari).
Despre faptul caci exista solutii solutii per n=2, posibil aceeasi poveste sa fie si per n>2, eu nus'
De luat in seama ca 2 e numar prim DAR par, asa proprietate restul numerelor prime nu au, si cred ca e bine de luat in seama caci per puterea 2 suma a doi termeni patrati nu se poate discompune in produs.
Pina ce ramine de sapat.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Obligatoriu chiar.meteor a scris:La cazul n=2, nu este aceeasi poveste ?! Oare nu daca (x,y,z)=1, atunci cel putin 2 factori nu sunt divizibili cu 2 (am dedus doar ca unul e par celelalte doi factori impari).
Iar pentru x, y, z soluții primitive ale ecuației, una din soluțiile x sau y este soluția pară ; z nu poate fi un număr par.
Mai mult, una din soluții se divide obligatoriu cu 3, una, sau aceeași se divide cu 4, iar cealaltă, sau chiar una dintre cele care se divide cu 3 și cu 4, se divide și cu 5.
Dacă vrei și demonstrația ți-o scriu, deși o poți deduce și singur.
Pentru situația în care una se divide cu 5 analizează ultima cifră, pentru cazul în care o soluție este divizibilă cu 3 folosești mica teoremă a lui Fermat, iar pentru cazul soluției care se divide cu 4 arăți că diferența a două pătrate perfecte care se divide cu 2, este divizibilă cu 4.
Generalizat, poți arăta că dacă diferența a două numere la puterea p se divide cu p, atunci această diferență se divide cel puțin cu p la pătrat.
2 este un număr prim, dar deși este par, aproape în toate cazurile unor afirmații privitoare la numerele prime, 2 se supune la aceeași regulă a afirmației.meteor a scris:De luat in seama ca 2 e numar prim DAR par, asa proprietate restul numerelor prime nu au, si cred ca e bine de luat in seama caci per puterea 2 suma a doi termeni patrati nu se poate discompune in produs.
Dacă suma a două pătrate perfecte nu s-ar putea descompune în produs, așa cum te exprimi tu și dacă am înțeles bine, atunci ar însemna că orice sumă de două pătrate perfecte este un număr prim, nu ?
Vrei contraexemple ?
Mă gândesc că nu, le găsești singur.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Poate ca.curiosul a scris:2 este un număr prim, dar deși este par, aproape în toate cazurile unor afirmații privitoare la numerele prime, 2 se supune la aceeași regulă a afirmației.meteor a scris:De luat in seama ca 2 e numar prim DAR par, asa proprietate restul numerelor prime nu au, si cred ca e bine de luat in seama caci per puterea 2 suma a doi termeni patrati nu se poate discompune in produs.
Dacă suma a două pătrate perfecte nu s-ar putea descompune în produs, așa cum te exprimi tu și dacă am înțeles bine, atunci ar însemna că orice sumă de două pătrate perfecte este un număr prim, nu ?
Vrei contraexemple ?
Mă gândesc că nu, le găsești singur.
Eu vau sa zic ca sa gasesti o formula generala la a^2+b^2 de descompunere in produs cred ca e pe semnul intrebarii, pina ce nu se vad ca are nimic cu demonstrarea , pur si simplu e o banueala.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Te referi la ceva asemănător ca în cazul diferenței ?meteor a scris:
Eu vau sa zic ca sa gasesti o formula generala la a^2+b^2 de descompunere in produs cred ca e pe semnul intrebarii, pina ce nu se vad ca are nimic cu demonstrarea , pur si simplu e o banueala.
Cum ar fi
Eu sunt de părere că nu există o formulă generalizată, ci doar particularizări, pentru că sunt și cazuri în care suma a două pătrate perfecte este un număr prim, dar nu este o regulă.
Acum îmi amintesc că parcă mi-am ridicat și eu mai demult o problemă asemănătoare.
Nu știu la ce concluzie am ajuns, la nivelul unor cazuri particulare, parcă.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Sa anlizam cazul:
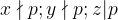
Ecuatia noastra fermantica o putem scrie:
!+M_{y}p-(p-1)!=z^{p}=(\lambda&space;\cdot&space;p)^{p})
Apoi:
^{p-1})p=2(p-1)!)
apoi:
^{p-1})p}{(p-1)!}&space;=2)
Toata chestia asta de:
^{p-1}) trebue sa fie un numar natural, fie ca il notam prin un oarecare
trebue sa fie un numar natural, fie ca il notam prin un oarecare 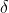
Avem:
!}=2)
Apare intrebarea: Poate fi un asa numar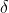 natural ?!
natural ?!
Parca am mai avut chindva la inceput un asa caz asemanator, eu cred ca nu poate fi un asa numar.
De aici rezulta caci pentru asa caz ecuatia nu are solutii, doar io' stiu per p=2, poateca ceva ar merge.
Sper ca nu am gresit pina aici cu nimic.
Daca, ceea ce am facut pina aici e corect, atunci ramin inca doua subcazuri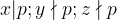 si
si 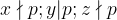 (defapt unul..), daca si ele se determina, demonstratia e finisata.
(defapt unul..), daca si ele se determina, demonstratia e finisata.
Ecuatia noastra fermantica o putem scrie:
Apoi:
apoi:
Toata chestia asta de:
Avem:
Apare intrebarea: Poate fi un asa numar
Parca am mai avut chindva la inceput un asa caz asemanator, eu cred ca nu poate fi un asa numar.
De aici rezulta caci pentru asa caz ecuatia nu are solutii, doar io' stiu per p=2, poateca ceva ar merge.
Sper ca nu am gresit pina aici cu nimic.
Daca, ceea ce am facut pina aici e corect, atunci ramin inca doua subcazuri
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Dacă scrii așa ecuația, asta înseamnă că ai plecat de la o egalitate de genul :
Pentru că ai aplicat teorema pe care ai menționat-o anterior, cea a lui Sierpinski :
Deci trebuie să reanalizezi raționamentul pentru că ecuațiacuriosul a scris:
Congruența corectă este
și nu
Rezultă din teorema lui Wilson :,
și mica teoremă a lui Fermat (corectă, nu greșită ca în mesajul anterior) :
Din cele două congruențe rezultă că, generalizat pentru orice a nedivizibil cu p prim.
nu este aceeași cu ecuația
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Membrul din stânga al ultimei identități este rațional și ajunge la o fracție ireductibilă prin simplificarea cu cel mai mare divizor comun al numărătorului și numitorului, pentru că numitorul nu-l conține pe p factor, în timp ce numărătorul îl conține, iar membrul din dreapta este întreg (2).
Dacă raționamentul tău ar fi corect, ar fi suficient să demonstreze teorema.
Dar vezi greșeala din mesajul anterior.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Demonstrația mai simplă, fără alte complicații, a faptului că egalitatea
Dacă p este mai mare ca 2, ceea ce analizăm de fapt, factorialul lui p-1 nu se divide cu p, ci cu orice număr prim mai mic ca p.
Ar demonstra teorema, dar greșeala raționamentului se află înaintea acestui pas.
este imposibilă, se explică prin faptul că membrul drept nu-l conține pe p factor, în timp ce membrul din stânga îl conține.
Dacă p este mai mare ca 2, ceea ce analizăm de fapt, factorialul lui p-1 nu se divide cu p, ci cu orice număr prim mai mic ca p.
Ar demonstra teorema, dar greșeala raționamentului se află înaintea acestui pas.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
http://fs.gallup.unm.edu/AUNFITN.pdf pag 14, repet se pare deja a 3 oara.
Teorema lui Serpinski spune:
Daca p e numar prim atunci:
!\equiv&space;0&space;(mod&space;p))
(eu spun) Adica:
!}{p}=M_{a})
apoi:
!)
Asa deci fii mai atent pe viitor, la fel fara sa ma supar astept critici.
Demonstratia ceea a ta a ireductibilitatii fractiei cred ca nu prea e ok trebue mai riguroasa, cea data de mine mai demult cred ca e buna (principiul fiecare se lauda pe sine ).
).
Teorema lui Serpinski spune:
Daca p e numar prim atunci:
(eu spun) Adica:
apoi:
Asa deci fii mai atent pe viitor, la fel fara sa ma supar astept critici.
Demonstratia ceea a ta a ireductibilitatii fractiei cred ca nu prea e ok trebue mai riguroasa, cea data de mine mai demult cred ca e buna (principiul fiecare se lauda pe sine
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Teorema lui Sierpinski, așa cum este ea scrisă acolo, este greșită.
Cel mai probabil este o greșeală de redactare.
Forma corectă a congruenței este
!\equiv&space;0(modp)}})
Mai întreabă, dacă chiar nu o poți deduce singur.
Vrei și contraexemple pentru varianta pe care o susții ca fiind corectă!\equiv&space;0(modp)}) ?
?
Nu are importanță care raționament este mai simplu, ci doar concluzia pe care o susțin.
Ce-i corect, e corect, nu te susțin doar de dragul de a te susține.
Cel mai probabil este o greșeală de redactare.
Forma corectă a congruenței este
Mai întreabă, dacă chiar nu o poți deduce singur.
Vrei și contraexemple pentru varianta pe care o susții ca fiind corectă
Nu are importanță care raționament este mai simplu, ci doar concluzia pe care o susțin.
Ce-i corect, e corect, nu te susțin doar de dragul de a te susține.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Privitor la cazul de mai sus anterior se pare ca asa e.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Demonstrația prin suma congruențelor, generalizat pentru orice a nedivizibil cu p, vine de la congruențele:
.......a^{p-1}\equiv&space;1&space;\\&space;(Wilson)...(p-1)!\equiv&space;-1&space;\end{cases}(mod\mathbf{p}))
Din suma termenilor congruențelor, rezultă congruența în mod p :
!\equiv&space;0&space;}(mod\mathbf{p}))
Pentru orice a nedivizibil cu p.
Din suma termenilor congruențelor, rezultă congruența în mod p :
Pentru orice a nedivizibil cu p.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Sa o luam de la capat.
Pentru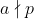 avem teoremele:
avem teoremele:
.......a^{p-1}-1\equiv&space;0&space;\\&space;(Serpinski)..a^{p-1}+(p-1)!\equiv&space;0&space;\end{cases}(mod\mathbf{p}))
Ceea ce se mai poate scrie:
!&space;\end{cases})
Inmultind ambele ecuatii avem:
}=M_{a'}M_{a''}p^{2}-M_{a&space;'}p!+M_{a''}p-(p-1)!)
Multiplii tot multipli ramin, deaceea ii scrim unde se poateca pe un multimplu:
}=M_{a}p^{2}+M_{a}p&space;-M_{a&space;}p!-(p-1)!)
Acum apare o intrebare (o mica dilema) poate fi considerat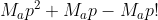 ca fiind un oarecare numar (multimplu) inmultit cu p ?! Ca este divizibil cu p e clar, dar ca multiplul e pozitiv cam e pe semnul intrebarii.
ca fiind un oarecare numar (multimplu) inmultit cu p ?! Ca este divizibil cu p e clar, dar ca multiplul e pozitiv cam e pe semnul intrebarii.
Pina la urma il vom nota ca multiplu, insa nu stim e pozitiv sau negativ, asa ca ecuatia mai putem scrie:
}=M_{a}p-(p-1)!)
Fachind mai departe acelasi truc, obtinem aceeasi si pentru :
}=M_{a}p-(p-1)!)
Sau la general spus:
}=M_{a}p-(p-1)!;\lambda&space;\geq&space;1)
Aceasta formula ne da voe sa demonstram pentru o multime de cazuri (cei drept doar pare), daca:
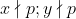 oarecare ar fi z.
oarecare ar fi z.
Pentru cazul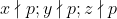 cu atit mai mult.
cu atit mai mult.
Adica, ecuatia:
}+y^{\lambda&space;(p-1)}=z^{\lambda&space;(p-1)})
Nu are solutii daca:
=1)
Ce nu trebue de uitat e faptul ca cel putin 2 termeni din ecuatia fermantica, pentru cazul chind (x,y,z)=1, nu sunt divizibili cu p.
Pentru
Ceea ce se mai poate scrie:
Inmultind ambele ecuatii avem:
Multiplii tot multipli ramin, deaceea ii scrim unde se poateca pe un multimplu:
Acum apare o intrebare (o mica dilema) poate fi considerat
Pina la urma il vom nota ca multiplu, insa nu stim e pozitiv sau negativ, asa ca ecuatia mai putem scrie:
Fachind mai departe acelasi truc, obtinem aceeasi si pentru :
Sau la general spus:
Aceasta formula ne da voe sa demonstram pentru o multime de cazuri (cei drept doar pare), daca:
Pentru cazul
Adica, ecuatia:
Nu are solutii daca:
Ce nu trebue de uitat e faptul ca cel putin 2 termeni din ecuatia fermantica, pentru cazul chind (x,y,z)=1, nu sunt divizibili cu p.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Din
}=M_{a}p-(p-1)!}&space;\\&space;\mathbf{x^{\lambda&space;(p-1)}+y^{\lambda&space;(p-1)}=z^{\lambda&space;(p-1)}}&space;\end{cases}\Rightarrow)
!+M_{y}p-(p-1)!=M_{z}p-(p-1)!})
=(p-1)!})
Egalitate evident imposibilă prin faptul că p nu este conținut factor în dreapta.
Dar doar dacă x, y, z nu se divid niciunul cu p.
Nici nu-ți trebuie alte complicații, folosești direct teorema lui Sierpinski.
Dar așa cum ți-am mai spus, aceasta demonstrează doar că una din soluții trebuie să fie obligatoriu divizibilă cu p, altfel, pentru acest caz general p-1, se ajunge la ultima egalitate de mai sus imposibilă.
Nu ai avansat prea mult, ai scris doar sub o altă formă un raționament pe care l-ai folosit anterior.
Egalitate evident imposibilă prin faptul că p nu este conținut factor în dreapta.
Dar doar dacă x, y, z nu se divid niciunul cu p.
Nici nu-ți trebuie alte complicații, folosești direct teorema lui Sierpinski.
Dar așa cum ți-am mai spus, aceasta demonstrează doar că una din soluții trebuie să fie obligatoriu divizibilă cu p, altfel, pentru acest caz general p-1, se ajunge la ultima egalitate de mai sus imposibilă.
Nu ai avansat prea mult, ai scris doar sub o altă formă un raționament pe care l-ai folosit anterior.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Nu e corect nimic. 
In ecuatia fermantica noi vorbim ca baza sa nu fie divizibila (sa nu fie multiplu) cu puterea.
Aici insa noi am cazut in capcana, aici nu vorbim ca baza sa nu fie multipla de putere, ci de ceva particular al puterii.
Ex:
Daca scriem ca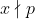 pentru cazul :
pentru cazul :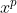 , atunci este corect (aplicind in eucuatia fermantica).
, atunci este corect (aplicind in eucuatia fermantica).
NU este insa corect chind spunem si aplicam teoremele de mai sus pentru cazul urmator:
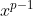
Aici (daca ne referim la ecuatia fermantica) atunci trebue ca) , INSA din punct de vedere a Micii teoreme a lui Fermat trebue ca:
, INSA din punct de vedere a Micii teoreme a lui Fermat trebue ca: 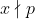 , ceea ce is doua lucruri diferite.
, ceea ce is doua lucruri diferite.
In ecuatia fermantica noi vorbim ca baza sa nu fie divizibila (sa nu fie multiplu) cu puterea.
Aici insa noi am cazut in capcana, aici nu vorbim ca baza sa nu fie multipla de putere, ci de ceva particular al puterii.
Ex:
Daca scriem ca
NU este insa corect chind spunem si aplicam teoremele de mai sus pentru cazul urmator:
Aici (daca ne referim la ecuatia fermantica) atunci trebue ca
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Nu-i așa simplă teorema asta, meteor !
Nu degeaba a rezistat atâtea secole, deși a fost analizată de minți fascinante ale matematicii.
Dar nu-i bai, la nivelul nostru e normal să greșim.
Vezi exemplul meu, cred c-am scris n demonstrații greșite.
Util ar fi să existe cineva care să ne arate și unde greșim, când nu putem să ne dăm seama singuri, cel puțin pentru moment.
Nu degeaba a rezistat atâtea secole, deși a fost analizată de minți fascinante ale matematicii.
Dar nu-i bai, la nivelul nostru e normal să greșim.
Vezi exemplul meu, cred c-am scris n demonstrații greșite.
Util ar fi să existe cineva care să ne arate și unde greșim, când nu putem să ne dăm seama singuri, cel puțin pentru moment.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
Re: Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
- Ca sa nu fie n subiecte cu n demonstratii gresite, deaceea si am deschis acest subiect, si un altul doar in care se va scrie demonstratiile corecte [daca vor fi].
Deaceea si am spus, ca suntem fermantisti
- Eu inca [visez, eh da' ce bine era sa fie daca cazurile anterioare ar fi fosr corecte] ca poate fi o cale foarte simpla.
Ecuatiile in intreg cred ca is asa ele, greu la rezolvat.
Deaceea si am spus, ca suntem fermantisti
- Eu inca [visez, eh da' ce bine era sa fie daca cazurile anterioare ar fi fosr corecte] ca poate fi o cale foarte simpla.
Ecuatiile in intreg cred ca is asa ele, greu la rezolvat.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
Pagina 2 din 2 •  1, 2
1, 2
 Subiecte similare
Subiecte similare» Demonstrațiile cazurilor particulare ale Marii teoreme a lui Fermat
» Demonstrația algebrică a marii teoreme a lui Fermat
» Cercetari asupra fenomenelor de qualia
» Demonstrația algebrică a marii teoreme a lui Fermat
» Cercetari asupra fenomenelor de qualia
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 2 din 2
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 