Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Meteorr Ieri la 21:34
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Joi 21 Noi 2024, 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la No_name în Ce anume "generează" legile fizice?
( 1 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 1 )
» Mesaj de la Abel Cavaşi în Daci nemuritori
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Dacu2 | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Abel Cavaşi |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| virgil | ||||
| Dacu2 | ||||
| Meteorr | ||||
| ilasus | ||||
| CAdi | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 38 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 38 Vizitatori :: 2 Motoare de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Demonstrațiile cazurilor particulare ale Marii teoreme a lui Fermat
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 1 din 1
 Demonstrațiile cazurilor particulare ale Marii teoreme a lui Fermat
Demonstrațiile cazurilor particulare ale Marii teoreme a lui Fermat
Deschid acest subiect ca să mai diversificăm o idee activitatea pe forum, precum și datorită faptului că unii pot fi interesați, sau chiar din pură curiozitate, să cunoască demonstrațiile elementare ale cazurilor particulare ale acestei teoreme, construite de vechii și marii matematicieni.
Acum nu am timp, dar voi scrie zilele acestea, cel mai probabil în week-end, două demonstrații foarte frumoase ale cazurilor n=3 și n=4, corecte de altfel, ale marii teoreme a lui Fermat, pe care le-am găsit într-un volum mai vechi de teorie a numerelor.
I-aș ruga de altfel, pe cei care știu de existența unor demonstrații corecte ale celorlalte cazuri particulare, n= 5, 7, ..., sau chiar și ale acestora (n= 3 și 4) , să atașeze un linc sau dacă au răbdare să le scrie complet.
Cred că este interesant să vedem cum au gândit acei matematicieni.
Acum nu am timp, dar voi scrie zilele acestea, cel mai probabil în week-end, două demonstrații foarte frumoase ale cazurilor n=3 și n=4, corecte de altfel, ale marii teoreme a lui Fermat, pe care le-am găsit într-un volum mai vechi de teorie a numerelor.
I-aș ruga de altfel, pe cei care știu de existența unor demonstrații corecte ale celorlalte cazuri particulare, n= 5, 7, ..., sau chiar și ale acestora (n= 3 și 4) , să atașeze un linc sau dacă au răbdare să le scrie complet.
Cred că este interesant să vedem cum au gândit acei matematicieni.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Demonstrațiile cazurilor particulare ale Marii teoreme a lui Fermat
Re: Demonstrațiile cazurilor particulare ale Marii teoreme a lui Fermat
OK.
Voi traduce, prezenta și comenta pentru început demonstrația elementară a teoremei lui Fermat pentru cazul n=3, exact așa cum este ea scrisă în volumul THEORIE DES NOMBRES - TOME SECOND - LE SECOND DEGRE BINAIRE, la pagina 600. (scuze pentru lipsa accentelor )
Pentru a ușura munca cititorului în a înțelege această demonstrație voi interveni pe alocuri încercând să explic mai clar de unde se deduc anumite implicații, scriind în paranteză, cu un font mai mic pentru a se distinge explicațiile mele complementare, de textul original al demonstrației.
Așadar :
Teorema lui Fermat pentru cazul n=3
Vom scrie ecuația lui Fermat sub o formă mai simetrică, schimbând z în -z :
\rightarrow&space;x^3+y^3+z^3=0})
Lema I :
Dacă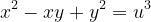 , cu D(x,y)=1, atunci una din valorile x, y, x-y este divizibilă cu 6.
, cu D(x,y)=1, atunci una din valorile x, y, x-y este divizibilă cu 6.
De fapt,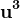 este primitiv reprezentabil prin forma (1, -1, 1), iar pentru că există doar o clasă de determinant 3, u este reprezentabil prin aceeași clasă și putem deduce reprezentarea primitivă a lui
este primitiv reprezentabil prin forma (1, -1, 1), iar pentru că există doar o clasă de determinant 3, u este reprezentabil prin aceeași clasă și putem deduce reprezentarea primitivă a lui 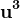 prin cea a lui u, prin formulele de multiplicare a formelor.
prin cea a lui u, prin formulele de multiplicare a formelor.
(În continuare, se face trimitere la un capitol din același volum în care sunt enunțate câteva teoreme, care demonstrează o parte din modalitățile și condițiile de multiplicare a formelor. Este un capitol întreg, destul de important în fundamentul acestei demonstrații, despre care nu voi detalia altceva aici.)
Punând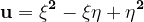
prin formula multiplicării formelor vom avea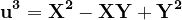 cu
cu
}&space;\end{cases})
Deci o reprezentare pentru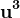 este, fie aceasta, fie una dintre acelea pe care le putem deduce prin substituții automorfe de (1, -1, 1), adică
este, fie aceasta, fie una dintre acelea pe care le putem deduce prin substituții automorfe de (1, -1, 1), adică
(Este vorba despre reprezentarea soluțiilor primitive X, Y pentru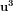 , unde acestea pot fi, fie exact soluțiile X și Y ale sistemului anterior, fie una este -X+Y, iar cealaltă este -x, fie una este -Y, iar cealaltă este X-Y.)
, unde acestea pot fi, fie exact soluțiile X și Y ale sistemului anterior, fie una este -X+Y, iar cealaltă este -x, fie una este -Y, iar cealaltă este X-Y.)
În prima reprezentare, valoarea celei de-a doua necunoscute, adică}) este divizibilă cu 6, în a doua reprezentare este diferența între cele două valori ale necunoscutelor, adică (-X+Y)+X, etc.
este divizibilă cu 6, în a doua reprezentare este diferența între cele două valori ale necunoscutelor, adică (-X+Y)+X, etc.
(Deci dacă soluțiile necunoscutelor nu sunt exact valorile X, Y ale sistemului deduse prin multiplicarea formei, caz în care a doua, Y, este sigur divizibilă cu 6, ca și în cazul celei de-a treia reprezentări unde una din soluții este -Y, în cealaltă reprezentare, diferența necunoscutelor este exact exprimarea lui Y, caz în care diferența x-y este divizibilă cu 6. Lema este corect și complet demonstrată.)
Lema II :
Dintre cele trei valori x, y, z, ca și soluții primitive ale ecuației (1), una este divizibilă cu 6.
(Aici se face o trimitere în subsolul paginii care spune :
Vedem ușor că una este divizibilă cu 2 și una care este divizibilă cu 3,
transformând în congruență mod 9 și insistând asupra faptului că^3\equiv&space;\pm&space;1)
(mod 9). Dar nu demonstrăm astfel că este aceeași valoare care se divide în același timp cu 2 și cu 3.
Deși nu este demonstrat aici, dacă cineva vrea să cunoască modul în care se demonstrează că una din soluții se divide cu 2 și una se divide cu 3, îi pot arăta ulterior cum se demonstrează asta.)
Este cel puțin una din cele trei valori care nu se divide nici cu 2, nici cu 3.
Presupunem că aceasta este z. Scriem :
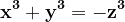 unde
unde
\rightarrow&space;(x+y)(x^2-xy+y^2)=-z^3})
Valorile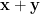 și
și 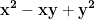 sunt prime între ele, altfel un factor prim comun ar trebui să dividă
sunt prime între ele, altfel un factor prim comun ar trebui să dividă
^2-(x^2-xy+y^2)}) sau
sau 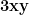 .
.
Dar acest factor nu poate fi trei, pentru că z nu este divizibil cu 3. (prin presupunerea inițială)
Deci ar trebui să fie unul din factorii lui x sau y și divizând x+y ar divide în același timp x și y ceea ce este imposibil.(prin faptul că x și y sunt prime între ele.)
În aceste condiții, egalitatea (2) impune ca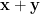 și
și 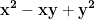 să fie ambele cuburi. Fie
să fie ambele cuburi. Fie
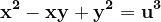 Astfel, după cum rezultă din lemma anterioară, dacă nici x, nici y nu este divizibil cu 6, atunci x-y trebuie să fie divizibil cu 6.
Astfel, după cum rezultă din lemma anterioară, dacă nici x, nici y nu este divizibil cu 6, atunci x-y trebuie să fie divizibil cu 6.
Dar aceasta este imposibil pentru că x și y sunt unul par și unul impar. (rezultă din faptul că z a fost presupus ca fiind soluția care nu se divide cu 6, acesta fiind impar, celelalte două nu pot fi ambele impare, sau ambele pare)
Aceste două leme demonstrate, revenim la ecuația (1) unde presupunem că z este soluția care se divide cu 6. În consecință, notăm :
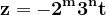 ,
, }) Avem așadar,
Avem așadar,
(x^2-xy+y^2)=2^{3m}3^{3n}t}) x,y,t nefiind divizibile nici cu 2, nici cu 3.
x,y,t nefiind divizibile nici cu 2, nici cu 3.
Căutăm cum se distribuie factorii 2 și 3 în primul membru. (pentru că acum s-a presupus că z este divizibil cu 6, deci este par, iar x, y, z prime între ele, rezultă că x și y sunt impare)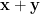 este par, în timp ce
este par, în timp ce 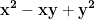 este impar, deci factorul
este impar, deci factorul 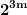 este conținut în
este conținut în 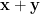 .
.
Pe de altă parte avem:
) ,
, ) Atunci
Atunci
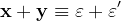
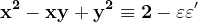
(Ultimele congruențe rezultă evident din cele anterioare, dar acest pas putea fi sărit în demonstrație, putându-se trece direct la a arăta că dacă z se divide cu 3, iar x și y nu, prin suma acestora două din urmă la puterea a treia, se ajunge la un număr divizibil cu 3, doar dacă unul este de forma 3k+1, iar celălalt de forma 3q-1, concluzie la care se ajunge și în continuare în demonstrația respectivă)
Nu putem avea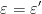 pentru că dacă ar fi așa niciunul din factorii
pentru că dacă ar fi așa niciunul din factorii 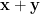 și
și 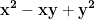 n-ar fi divizibili cu 3 (deci nici z). Avem așadar
n-ar fi divizibili cu 3 (deci nici z). Avem așadar 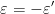 .
.
Pentru că nimic nu distinge încă x de y, putem presupune că
\rightarrow&space;\begin{cases}&space;\mathbf{x\equiv&space;1}\\&space;\mathbf{y\equiv&space;-1}&space;\end{cases}(mod3)) Atunci cei doi factori
Atunci cei doi factori 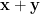 și
și 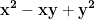 sunt ambii divizibili cu 3. Dar al doilea nu este divizibil cu 9, pentru că notând x=3h+1 și y=3k-1, se ajunge la
sunt ambii divizibili cu 3. Dar al doilea nu este divizibil cu 9, pentru că notând x=3h+1 și y=3k-1, se ajunge la
+3}) Pe de altă parte,
Pe de altă parte, 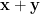 și
și 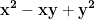 nu pot avea alți factori comuni cu excepția lui 3, pentru că așa cum am văzut mai sus, un alt factor comun ar divide 3xy.
nu pot avea alți factori comuni cu excepția lui 3, pentru că așa cum am văzut mai sus, un alt factor comun ar divide 3xy.
(O mică paranteză, toată această ultimă parte, și nu numai, poate fi demonstrată mult mai simplu și ușor de înțeles, deși și de aici rezultă destul de evident. Faptul că p prim poate fi singurul factor comun atât în dezvoltarea diferenței, cât și a sumei a două numere prime între ele la puterea p, s-a demonstrat generalizat și mult mai simplu chiar pe acest forum, de către Mezei Geza. )
Rezultă din toate acestea că :
\rightarrow&space;\begin{cases}&space;\mathbf{&space;x+y=2^{3m}3^{3n-1}u^3}&space;\\&space;\mathbf{x^2-xy+y^2=3v^3}&space;\end{cases}) u, v nefiind divizibile nici cu 2, nici cu 3 și sunt prime între ele.
u, v nefiind divizibile nici cu 2, nici cu 3 și sunt prime între ele.
A doua ecuație a sistemului se scrie :
^2-\left&space;(&space;\frac{2x-y}{3}&space;\right&space;)\left&space;(&space;\frac{x+y}{3}&space;\right&space;)+\left&space;(&space;\frac{x+y}{3}&space;\right&space;)^2=v^3}) valorile
valorile }) și
și }) fiind numere întregi așa cum rezultă din sistemul (3).
fiind numere întregi așa cum rezultă din sistemul (3).
Atunci, ca mai sus, avem pentru v expresia :
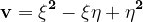 și pentru
și pentru }) și
și }) unul din sistemele următoare de valori :
unul din sistemele următoare de valori :
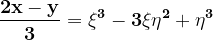
}) sau
sau
+3\xi&space;\eta&space;(\xi&space;-\eta&space;)})
}) sau
sau
})
-3\xi&space;\eta&space;(\xi&space;-\eta&space;)}) unde sistemele precedente de valori schimbă semnele și este inutil de a scrie pentru că le putem deduce din cele precedente schimbând semnele lui
unde sistemele precedente de valori schimbă semnele și este inutil de a scrie pentru că le putem deduce din cele precedente schimbând semnele lui 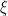 și
și 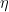 .
.
Din aceste trei sisteme de valori, ultimele două sunt inacceptabile.
De fapt, din al doilea se ajunge la
}) de unde
de unde
+3y}) unde
unde
+3y}) egalitate imposibilă pentru că termenii
egalitate imposibilă pentru că termenii 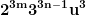 și
și }) sunt divizibili cu 9, în timp ce 3y nu este (pentru că y nu se divide cu 3, dacă am presupus că z se divide cu 6).
sunt divizibili cu 9, în timp ce 3y nu este (pentru că y nu se divide cu 3, dacă am presupus că z se divide cu 6).
Imposibilitatea celui de-al treilea sistem se vede scriind de asemenea :+3x}) .
.
Rămâne așadar :
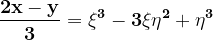 ;
; }) Atunci prima ecuație a sistemului (4) devine :
Atunci prima ecuație a sistemului (4) devine :
(din a doua ecuație de mai sus și din prima din sistemul (4), de fapt, se ajunge la)
=2^{3m}3^{3(n-1)}u^3}) Oricare doi din factorii primului membru
Oricare doi din factorii primului membru &space;}) sunt valori prime între ele, altfel un factor comun al acelor numere ar divide x și y. Deci oricare dintre ele este un cub și avem (pentru că al doilea membru este un cub) :
sunt valori prime între ele, altfel un factor comun al acelor numere ar divide x și y. Deci oricare dintre ele este un cub și avem (pentru că al doilea membru este un cub) :
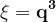
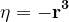
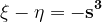
\rightarrow&space;qrs=2^m3^{n-1}u&space;}) unde factorul 3 intră doar într-unul din factorii q, r, s.
unde factorul 3 intră doar într-unul din factorii q, r, s.
Avem atunci
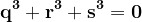 ecuație de aceeași formă ca ecuația inițială (1). Valorile necunoscutelor sunt prime între ele două câte două. Mai mult, ele sunt toate diferite de 0, pentru că altfel u ar fi nul și în consecință, de asemenea și z. Dar cele trei valori q, r, s, care ar conține factorul 3, l-ar conține doar la o putere n-1, cum rezultă din egalitatea (5).
ecuație de aceeași formă ca ecuația inițială (1). Valorile necunoscutelor sunt prime între ele două câte două. Mai mult, ele sunt toate diferite de 0, pentru că altfel u ar fi nul și în consecință, de asemenea și z. Dar cele trei valori q, r, s, care ar conține factorul 3, l-ar conține doar la o putere n-1, cum rezultă din egalitatea (5).
Astfel am dedus din soluțiile presupuse ale ecuației (1), alte soluții, din care niciuna nu este nulă, pentru aceeași ecuație și unde factorul 3 ar fi conținut cu un exponent diminuat cu o unitate.
Din aproape în aproape am ajunge așadar, la soluții pentru această ecuație nedivizibile cu 3, ceea ce este imposibil.
Corolar:
Teorema lui Fermat este adevărată pentru toate valorile de n care se divid cu 3.
Asta este demonstrația așa cum este ea scrisă în acel volum.
Acum, ajuns încă o dată la finalul ei, aș avea totuși o nelămurire.
Faptul că nu reiese de nicăieri că aceeași soluție se divide și cu 3, și cu 2 este oarecum irelevant pentru că demonstrația nu se bazează pe factorul 2, ci pe cel cu 3. Ar fi fost frumos să fie demonstrat și faptul că, obligatoriu, una din soluții trebuie să se dividă cu 3, pentru că, după cum am văzut și la finalul acesteia, demonstrația, în tot ansamblul ei, bazează pe această soluție divizibilă cu 3.
Dar nici asta nu e o problemă, pentru că acest lucru îl pot demonstra și eu, într-adevăr destul de ușor.
Dar cred că demonstrația este incompletă, pentru că după demonstrarea celor două leme, demonstrația se bazează până la final doar pe presupunerea că z se divide cu 6, ajungându-se la a se arăta imposibilitatea acestui lucru. Dar din a doua lemă rezultă că una din soluțiile x, y, z una se divide cu 6. Demonstrația nu a luat în calcul cazul în care soluția divizibilă cu 6 este una din soluțiile x sau y, ci doar cazul în care z se divide cu 6.
Probabil că demonstrația s-ar fi bazat pe același raționament, ajungându-se la reprezentări asemănătoare prin formulele de multiplicare a formelor.
Îmi scapă mie ceva, sau am dreptate, demonstrația nu ia în calcul situația în care x sau y se divide cu 6 ?
Voi ce ziceți ?
Voi traduce, prezenta și comenta pentru început demonstrația elementară a teoremei lui Fermat pentru cazul n=3, exact așa cum este ea scrisă în volumul THEORIE DES NOMBRES - TOME SECOND - LE SECOND DEGRE BINAIRE, la pagina 600. (scuze pentru lipsa accentelor )
Pentru a ușura munca cititorului în a înțelege această demonstrație voi interveni pe alocuri încercând să explic mai clar de unde se deduc anumite implicații, scriind în paranteză, cu un font mai mic pentru a se distinge explicațiile mele complementare, de textul original al demonstrației.
Așadar :
Teorema lui Fermat pentru cazul n=3
Vom scrie ecuația lui Fermat sub o formă mai simetrică, schimbând z în -z :
Lema I :
Dacă
De fapt,
(În continuare, se face trimitere la un capitol din același volum în care sunt enunțate câteva teoreme, care demonstrează o parte din modalitățile și condițiile de multiplicare a formelor. Este un capitol întreg, destul de important în fundamentul acestei demonstrații, despre care nu voi detalia altceva aici.)
Punând
prin formula multiplicării formelor vom avea
Deci o reprezentare pentru
X,Y sau -X+Y, -X sau -Y, X-Y
unde unul din cele trei sisteme schimbă semnul.(Este vorba despre reprezentarea soluțiilor primitive X, Y pentru
În prima reprezentare, valoarea celei de-a doua necunoscute, adică
(Deci dacă soluțiile necunoscutelor nu sunt exact valorile X, Y ale sistemului deduse prin multiplicarea formei, caz în care a doua, Y, este sigur divizibilă cu 6, ca și în cazul celei de-a treia reprezentări unde una din soluții este -Y, în cealaltă reprezentare, diferența necunoscutelor este exact exprimarea lui Y, caz în care diferența x-y este divizibilă cu 6. Lema este corect și complet demonstrată.)
Lema II :
Dintre cele trei valori x, y, z, ca și soluții primitive ale ecuației (1), una este divizibilă cu 6.
(Aici se face o trimitere în subsolul paginii care spune :
Vedem ușor că una este divizibilă cu 2 și una care este divizibilă cu 3,
transformând în congruență mod 9 și insistând asupra faptului că
(mod 9). Dar nu demonstrăm astfel că este aceeași valoare care se divide în același timp cu 2 și cu 3.
Deși nu este demonstrat aici, dacă cineva vrea să cunoască modul în care se demonstrează că una din soluții se divide cu 2 și una se divide cu 3, îi pot arăta ulterior cum se demonstrează asta.)
Este cel puțin una din cele trei valori care nu se divide nici cu 2, nici cu 3.
Presupunem că aceasta este z. Scriem :
Valorile
Dar acest factor nu poate fi trei, pentru că z nu este divizibil cu 3. (prin presupunerea inițială)
Deci ar trebui să fie unul din factorii lui x sau y și divizând x+y ar divide în același timp x și y ceea ce este imposibil.(prin faptul că x și y sunt prime între ele.)
În aceste condiții, egalitatea (2) impune ca
Dar aceasta este imposibil pentru că x și y sunt unul par și unul impar. (rezultă din faptul că z a fost presupus ca fiind soluția care nu se divide cu 6, acesta fiind impar, celelalte două nu pot fi ambele impare, sau ambele pare)
Aceste două leme demonstrate, revenim la ecuația (1) unde presupunem că z este soluția care se divide cu 6. În consecință, notăm :
Căutăm cum se distribuie factorii 2 și 3 în primul membru. (pentru că acum s-a presupus că z este divizibil cu 6, deci este par, iar x, y, z prime între ele, rezultă că x și y sunt impare)
Pe de altă parte avem:
(Ultimele congruențe rezultă evident din cele anterioare, dar acest pas putea fi sărit în demonstrație, putându-se trece direct la a arăta că dacă z se divide cu 3, iar x și y nu, prin suma acestora două din urmă la puterea a treia, se ajunge la un număr divizibil cu 3, doar dacă unul este de forma 3k+1, iar celălalt de forma 3q-1, concluzie la care se ajunge și în continuare în demonstrația respectivă)
Nu putem avea
Pentru că nimic nu distinge încă x de y, putem presupune că
(O mică paranteză, toată această ultimă parte, și nu numai, poate fi demonstrată mult mai simplu și ușor de înțeles, deși și de aici rezultă destul de evident. Faptul că p prim poate fi singurul factor comun atât în dezvoltarea diferenței, cât și a sumei a două numere prime între ele la puterea p, s-a demonstrat generalizat și mult mai simplu chiar pe acest forum, de către Mezei Geza. )
Rezultă din toate acestea că :
A doua ecuație a sistemului se scrie :
Atunci, ca mai sus, avem pentru v expresia :
Din aceste trei sisteme de valori, ultimele două sunt inacceptabile.
De fapt, din al doilea se ajunge la
Imposibilitatea celui de-al treilea sistem se vede scriind de asemenea :
Rămâne așadar :
(din a doua ecuație de mai sus și din prima din sistemul (4), de fapt, se ajunge la)
Avem atunci
Astfel am dedus din soluțiile presupuse ale ecuației (1), alte soluții, din care niciuna nu este nulă, pentru aceeași ecuație și unde factorul 3 ar fi conținut cu un exponent diminuat cu o unitate.
Din aproape în aproape am ajunge așadar, la soluții pentru această ecuație nedivizibile cu 3, ceea ce este imposibil.
Corolar:
Teorema lui Fermat este adevărată pentru toate valorile de n care se divid cu 3.
Asta este demonstrația așa cum este ea scrisă în acel volum.
Acum, ajuns încă o dată la finalul ei, aș avea totuși o nelămurire.
Faptul că nu reiese de nicăieri că aceeași soluție se divide și cu 3, și cu 2 este oarecum irelevant pentru că demonstrația nu se bazează pe factorul 2, ci pe cel cu 3. Ar fi fost frumos să fie demonstrat și faptul că, obligatoriu, una din soluții trebuie să se dividă cu 3, pentru că, după cum am văzut și la finalul acesteia, demonstrația, în tot ansamblul ei, bazează pe această soluție divizibilă cu 3.
Dar nici asta nu e o problemă, pentru că acest lucru îl pot demonstra și eu, într-adevăr destul de ușor.
Dar cred că demonstrația este incompletă, pentru că după demonstrarea celor două leme, demonstrația se bazează până la final doar pe presupunerea că z se divide cu 6, ajungându-se la a se arăta imposibilitatea acestui lucru. Dar din a doua lemă rezultă că una din soluțiile x, y, z una se divide cu 6. Demonstrația nu a luat în calcul cazul în care soluția divizibilă cu 6 este una din soluțiile x sau y, ci doar cazul în care z se divide cu 6.
Probabil că demonstrația s-ar fi bazat pe același raționament, ajungându-se la reprezentări asemănătoare prin formulele de multiplicare a formelor.
Îmi scapă mie ceva, sau am dreptate, demonstrația nu ia în calcul situația în care x sau y se divide cu 6 ?
Voi ce ziceți ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Demonstrațiile cazurilor particulare ale Marii teoreme a lui Fermat
Re: Demonstrațiile cazurilor particulare ale Marii teoreme a lui Fermat
Cred că voi reveni ulterior asupra demonstrației anterioare, pentru că nu sunt complet convins, demonstrația fiind totuși destul de greoaie și dificil de înțeles. Eventual voi încerca, pe baza principiului pe care a fost construită, să o reproduc într-un mod mai clar, unde implicațiile rezultă printr-un mod mai ușor de înțeles, analizând și situația în care una din valorile x sau y este soluția care se divide cu 3.
În continuare, voi prezenta demonstrația cazului n=4, așa cum este scrisă acolo, fără alte comentarii personale, demonstrație care este bazată pe principiul dezvoltat de Fermat însuși, reprodusă de Frenicle de Bessy, ceva mai simplă și mai ușor de înțeles.
Teorema lui Fermat pentru cazul n=4
Acestă teoremă se enunță :
Ecuația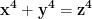 nu are alte soluții, cu excepția celor unde una din necunoscutele x sau y are o valoare nulă. Vom demonstra acest rezultat pentru o ecuație mai generală, și anume
nu are alte soluții, cu excepția celor unde una din necunoscutele x sau y are o valoare nulă. Vom demonstra acest rezultat pentru o ecuație mai generală, și anume
\rightarrow&space;x^4+y^4=z^2}) Această ecuație nu are alte soluții cu excepția celor pentru care una din valorile x sau y este nulă.
Această ecuație nu are alte soluții cu excepția celor pentru care una din valorile x sau y este nulă.
Putem presupune că soluțiile x, y, z sunt prime între ele.
Presupunem de fapt, că ele ar avea un factor prim comun p. Punând
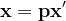 ,
, 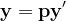 ,
, 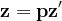 ecuația devine
ecuația devine
={z}'^2}) Deci z' trebuie să se dividă cu p. Notând z'=pz" se ajunge la
Deci z' trebuie să se dividă cu p. Notând z'=pz" se ajunge la
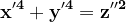 Dacă valorile x' , y' , z" ar avea încă un factor prim comun am repeta raționamentul până când s-ar ajunge la o ecuație de forma (1) în care valorile necunoscutelor n-ar mai avea niciun factor prim comun.
Dacă valorile x' , y' , z" ar avea încă un factor prim comun am repeta raționamentul până când s-ar ajunge la o ecuație de forma (1) în care valorile necunoscutelor n-ar mai avea niciun factor prim comun.
În particular, valorile celor trei necunoscute nu sunt pare; ele nu pot fi două pare și unul impar și nici toate trei impare. Deci este o soluție pară și două impare.
Transformând ecuația în congruență (mod 4) observăm că nu este posibil ca x și y să aibă valori impare și z o valoare pară. Deci z are o valoare impară, una din necunoscutele x sau y, spre exemplu x, are o valoare pară și cealaltă necunoscută, y, are o valoare impară. Fie
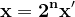 y fiind impar. Ecuația devine
y fiind impar. Ecuația devine
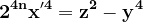 x' , y, z având valori impare, fără factori comuni. Vom face demonstrația pentru o ecuație mai generală:
x' , y, z având valori impare, fără factori comuni. Vom face demonstrația pentru o ecuație mai generală:
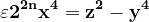
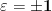 , n>0 , x, y, z impare fără factori comuniAceastă ecuație se scrie :
, n>0 , x, y, z impare fără factori comuniAceastă ecuație se scrie :
\rightarrow&space;\varepsilon&space;2^{2n}x^4=(z-y^2)(z+y^2)}) Putem observa că cel mai mare divizor comun al lui
Putem observa că cel mai mare divizor comun al lui }) și
și }) este egal cu 2. Deci avem :
este egal cu 2. Deci avem :
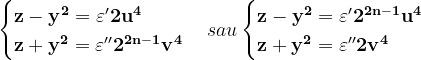
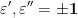 , u și v impare, prime între eleDar al doilea sistem derivă din primul schimbând z în -z,
, u și v impare, prime între eleDar al doilea sistem derivă din primul schimbând z în -z, 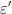 în
în 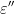 , u cu v și v cu u. Este suficient așadar, de a considera doar primul sistem. Ajungem la
, u cu v și v cu u. Este suficient așadar, de a considera doar primul sistem. Ajungem la
\rightarrow&space;y^2=&space;{\varepsilon&space;}''2^{2n-2}v^4-{\varepsilon&space;}'u^4}) Dacă n>1, transformând această ecuație în congruență (mod 4) se obține
Dacă n>1, transformând această ecuație în congruență (mod 4) se obține
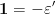 (mod 4)Deci
(mod 4)Deci 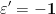 și ecuația (3) devine :
și ecuația (3) devine :
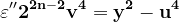 adică o ecuație de aceeași formă cu ecuația (2), dar exponentul n diminuat cu o unitate. Repetând acest procedeu ori de câte ori este necesar ajungem la o ecuație de aceeași formă cu ecuația (2), însă unde n=1, adică
adică o ecuație de aceeași formă cu ecuația (2), dar exponentul n diminuat cu o unitate. Repetând acest procedeu ori de câte ori este necesar ajungem la o ecuație de aceeași formă cu ecuația (2), însă unde n=1, adică
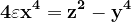 (x, y, z impare)Ori transformând aceasta din urmă în congruență mod 8, observăm că ea este imposibilă.
(x, y, z impare)Ori transformând aceasta din urmă în congruență mod 8, observăm că ea este imposibilă.
Teorema lui Fermat este, așadar, adevărată pentru n=4.
Remarcă
Este evident că dacă teorema lui Fermat este adevărată pentru o valoare de n, ea este de asemenea și pentru valoarea lui n multiplul precedentului. Deci teorema lui Fermat este adevărată pentru toate valorile lui n divizibile cu 4.
În continuare, voi prezenta demonstrația cazului n=4, așa cum este scrisă acolo, fără alte comentarii personale, demonstrație care este bazată pe principiul dezvoltat de Fermat însuși, reprodusă de Frenicle de Bessy, ceva mai simplă și mai ușor de înțeles.
Teorema lui Fermat pentru cazul n=4
Acestă teoremă se enunță :
Ecuația
Putem presupune că soluțiile x, y, z sunt prime între ele.
Presupunem de fapt, că ele ar avea un factor prim comun p. Punând
În particular, valorile celor trei necunoscute nu sunt pare; ele nu pot fi două pare și unul impar și nici toate trei impare. Deci este o soluție pară și două impare.
Transformând ecuația în congruență (mod 4) observăm că nu este posibil ca x și y să aibă valori impare și z o valoare pară. Deci z are o valoare impară, una din necunoscutele x sau y, spre exemplu x, are o valoare pară și cealaltă necunoscută, y, are o valoare impară. Fie
Teorema lui Fermat este, așadar, adevărată pentru n=4.
Remarcă
Este evident că dacă teorema lui Fermat este adevărată pentru o valoare de n, ea este de asemenea și pentru valoarea lui n multiplul precedentului. Deci teorema lui Fermat este adevărată pentru toate valorile lui n divizibile cu 4.
Ultima editare efectuata de catre curiosul in Dum 06 Oct 2013, 13:19, editata de 1 ori (Motiv : eliminat paranteze care reproduc codul unui emoticon)
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Subiecte similare
Subiecte similare» Cercetari asupra demonstratiei a cazurilor particulare si sau generale a Marii Teoreme a lui Fermat
» Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
» Despre demonstrațiile lui meteor
» Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
» Despre demonstrațiile lui meteor
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 