Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Meteorr Ieri la 21:34
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Joi 21 Noi 2024, 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la eugen în Global warming is happening?
( 1 )
» Mesaj de la CAdi în TEORIA CONSPIRATIEI NU ESTE UN MIT...
( 1 )
» Mesaj de la CAdi în Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| Dacu2 | ||||
| eugen | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Abel Cavaşi |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| virgil | ||||
| Dacu2 | ||||
| Meteorr | ||||
| ilasus | ||||
| CAdi | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 46 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 46 Vizitatori :: 1 Motor de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
5 participanți
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 1 din 2
Pagina 1 din 2 • 1, 2 
 Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Ce nu-ți convine la demonstrația asta Dacule ?
Faptul că este plecată de la sistemul tău ?
Faptul că ai falsa părere că meritele tale nu ar mai fi la fel de mari ?
Greșești.
Acesta este un cont nou.
Vedeți voi (administratorii) care le eliminați.
Dacă vreți, puteți să le eliminați pe amândouă,
n-am nimic împotrivă.
În orice triunghi este adevărată relația :
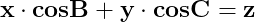
și de asemenea
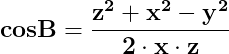
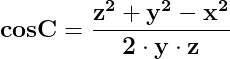
unde x, y, z sunt laturile triunghiului, iar cosB și cosC,
cosinusurile unghiurilor formate de laturile x și z, respectiv y și z.
Deci în orice triunghi este valabilă egalitatea (1):
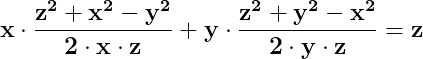
Dacă între laturile x, y, z ale unui triunghi este adevărată și egalitatea :
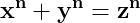
rezultă că este adevărată și egalitatea (2):
![\dpi{150} \mathbf{\frac{z^n}{z^{n-1}}=\frac{x^n+y^n}{z^{n-1}}=\frac{x^n}{z^{n-1}}+\frac{y^n}{z^{n-1}}=\left [ x\cdot \frac{x^{n-1}}{z^{n-1}}+y\cdot \frac{y^{n-1}}{z^{n-1}}=z \right ]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{\frac{z^n}{z^{n-1}}=\frac{x^n+y^n}{z^{n-1}}=\frac{x^n}{z^{n-1}}+\frac{y^n}{z^{n-1}}=\left [ x\cdot \frac{x^{n-1}}{z^{n-1}}+y\cdot \frac{y^{n-1}}{z^{n-1}}=z \right ]})
Pentru că
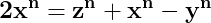
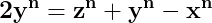
atunci putem scrie
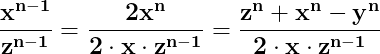
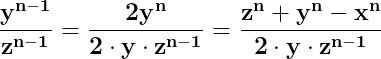
Înlocuind în egalitatea (2), ajungem să stabilim că dacă între laturile x, y, z ale unui triunghi este adevărată
egalitatea ,
,
atunci în acel tiunghi este adevărată egalitatea (3):
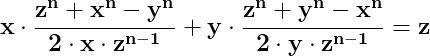
În concluzie, în triunghiul în care are loc și egalitatea , atunci în acel triunghi sunt simultan adevărate egalitățile (1)și
, atunci în acel triunghi sunt simultan adevărate egalitățile (1)și
(3):
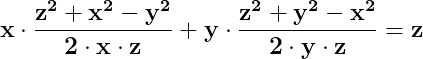
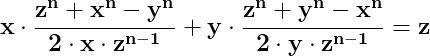
De unde rezultă că :
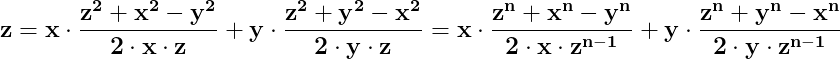
Pentru că din egalitatea de mai sus, în orice triunghi este adevărată relația
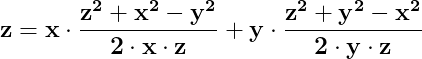
rezultă evident că pentru n diferit de 2, în același triunghi nu poate fi adevărată egalitatea :
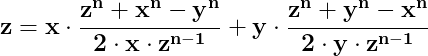
Deși x, y, z nu pot fi laturile unui triunghi dacă x+y=z,
pentru n=1, ecuația are soluții reale.
are soluții reale.
Pentru că laturile x, y, z ale triunghiului pot fi oricare numere reale,
ce îndeplinesc condițiile x+y>z , y+z>x , x+z>y,
ecuația nu are soluții
nu are soluții
reale pentru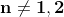 .
.
Q.E.D
Faptul că este plecată de la sistemul tău ?
Faptul că ai falsa părere că meritele tale nu ar mai fi la fel de mari ?
Greșești.
Acesta este un cont nou.
Vedeți voi (administratorii) care le eliminați.
Dacă vreți, puteți să le eliminați pe amândouă,
n-am nimic împotrivă.
În orice triunghi este adevărată relația :
și de asemenea
unde x, y, z sunt laturile triunghiului, iar cosB și cosC,
cosinusurile unghiurilor formate de laturile x și z, respectiv y și z.
Deci în orice triunghi este valabilă egalitatea (1):
Dacă între laturile x, y, z ale unui triunghi este adevărată și egalitatea :
rezultă că este adevărată și egalitatea (2):
Pentru că
atunci putem scrie
Înlocuind în egalitatea (2), ajungem să stabilim că dacă între laturile x, y, z ale unui triunghi este adevărată
egalitatea
atunci în acel tiunghi este adevărată egalitatea (3):
În concluzie, în triunghiul în care are loc și egalitatea
(3):
De unde rezultă că :
Pentru că din egalitatea de mai sus, în orice triunghi este adevărată relația
rezultă evident că pentru n diferit de 2, în același triunghi nu poate fi adevărată egalitatea :
Deși x, y, z nu pot fi laturile unui triunghi dacă x+y=z,
pentru n=1, ecuația
Pentru că laturile x, y, z ale triunghiului pot fi oricare numere reale,
ce îndeplinesc condițiile x+y>z , y+z>x , x+z>y,
ecuația
reale pentru
Q.E.D
Curi_osul- Mulţumit de forum : Numarul mesajelor : 7




Puncte : 12822
Data de inscriere : 22/03/2013
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Fermat e mort demult timp, s-a si demonstrat conjectura lui, lasati-l odata si odata in pace, ca sughitie saracul pe lumea aia la greu
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Noi suntem vii!Nu vrei să mori de curiozitate să încerci a găsi o demonstraţie bazată pe cunostinţe de matematică elementară? 
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22433
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Demonstrația are nevoie totuși de anumite completări, pentru a consolida validitatea concluziilor.
În orice triunghi este adevărată relația :
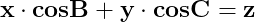
și de asemenea
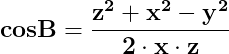
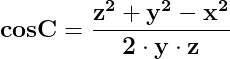
unde x, y, z sunt laturile triunghiului, iar cosB și cosC,
cosinusurile unghiurilor formate de laturile x și z, respectiv y și z.
Deci în orice triunghi este adevărată egalitatea (1):
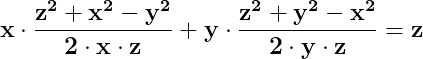
Dacă între laturile x, y, z ale unui triunghi este adevărată și egalitatea :
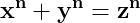
rezultă că este adevărată și egalitatea (2):
![\dpi{150} \mathbf{\frac{z^n}{z^{n-1}}=\frac{x^n+y^n}{z^{n-1}}=\frac{x^n}{z^{n-1}}+\frac{y^n}{z^{n-1}}=\left [ x\cdot \frac{x^{n-1}}{z^{n-1}}+y\cdot \frac{y^{n-1}}{z^{n-1}}=z \right ]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{\frac{z^n}{z^{n-1}}=\frac{x^n+y^n}{z^{n-1}}=\frac{x^n}{z^{n-1}}+\frac{y^n}{z^{n-1}}=\left [ x\cdot \frac{x^{n-1}}{z^{n-1}}+y\cdot \frac{y^{n-1}}{z^{n-1}}=z \right ]})
Pentru că
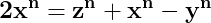
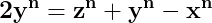
atunci putem scrie
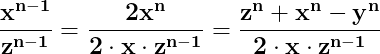
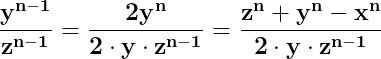
Înlocuind în egalitatea (2), ajungem să stabilim că dacă între laturile x, y, z ale unui triunghi este adevărată relația ,
,
atunci în acel tiunghi este adevărată și egalitatea (3):
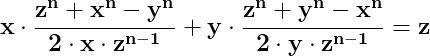
În concluzie, în triunghiul în care are loc și egalitatea , atunci în acel triunghi sunt simultan adevărate relațiile (1)și (3):
, atunci în acel triunghi sunt simultan adevărate relațiile (1)și (3):
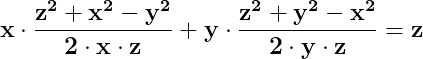
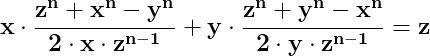
De unde rezultă că :
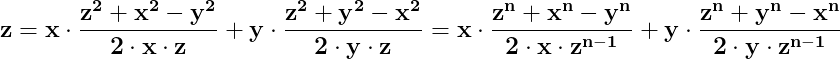

![\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]=y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]=y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]})
Pentru oricare x, y, z, n reale pozitive, ca și laturi ale unui triunghi, pentru relația de mai sus putem stabili condițiile și concluziile :
Dacă
\Rightarrow \begin{cases} & \text{ } \mathbf{\frac{z^2+x^2-y^2}{2\cdot x\cdot z}= \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}} \\ & \text{ } \\ & \text{ } \mathbf{\frac{z^2+y^2-x^2}{2\cdot y\cdot z}= \frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}} \end{cases})
de unde rezultă că pentru cazul n=2 este posibilă egalitatea :
![\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]=y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]=y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]})
Dacă
\Rightarrow \begin{cases} & \text{ } \mathbf{\frac{z^2+x^2-y^2}{2\cdot x\cdot z}> \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}} \\ & \text{ } \\ & \text{ } \mathbf{\frac{z^2+y^2-x^2}{2\cdot y\cdot z}> \frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}} \end{cases})
de unde rezultă că dacă n>2, egalitatea de mai jos nu poate fi adevărată pentru că unul din termeni este pozitiv, iar celălalt este negativ :
![\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]\neq y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]\neq y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]})
Dacă
\Rightarrow \begin{cases} & \text{ } \mathbf{\frac{z^2+x^2-y^2}{2\cdot x\cdot z}< \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}} \\ & \text{ } \\ & \text{ } \mathbf{\frac{z^2+y^2-x^2}{2\cdot y\cdot z}< \frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}} \end{cases})
de unde rezultă că pentru n<2, la fel ca în cazul anterior, egalitatea de mai jos nu poate fi adevărată pentru că unul din termeni este pozitiv, iar celălalt este negativ :
![\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]\neq y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]\neq y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]})
Pentru n=1, ecuația are soluții reale.
are soluții reale.
Putem așadar, concluziona că pentru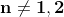
ecuația nu are soluții reale pozitive x, y, z, n.
nu are soluții reale pozitive x, y, z, n.
Dar dacă ecuația ar admite soluții reale negative,
separându-le de o parte și de alta a egalității,
sau înmulțind termenii cu (-1) în cazul în care toți termenii sunt negativi,
se ajunge la o ecuație cu termeni pozitivi, ca în cazul de mai sus.
În concluzie, putem generaliza că pentru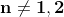
ecuația nu are soluții reale x, y, z, n.
nu are soluții reale x, y, z, n.
În orice triunghi este adevărată relația :
și de asemenea
unde x, y, z sunt laturile triunghiului, iar cosB și cosC,
cosinusurile unghiurilor formate de laturile x și z, respectiv y și z.
Deci în orice triunghi este adevărată egalitatea (1):
Dacă între laturile x, y, z ale unui triunghi este adevărată și egalitatea :
rezultă că este adevărată și egalitatea (2):
Pentru că
atunci putem scrie
Înlocuind în egalitatea (2), ajungem să stabilim că dacă între laturile x, y, z ale unui triunghi este adevărată relația
atunci în acel tiunghi este adevărată și egalitatea (3):
În concluzie, în triunghiul în care are loc și egalitatea
De unde rezultă că :
Pentru oricare x, y, z, n reale pozitive, ca și laturi ale unui triunghi, pentru relația de mai sus putem stabili condițiile și concluziile :
Dacă
de unde rezultă că pentru cazul n=2 este posibilă egalitatea :
Dacă
de unde rezultă că dacă n>2, egalitatea de mai jos nu poate fi adevărată pentru că unul din termeni este pozitiv, iar celălalt este negativ :
Dacă
de unde rezultă că pentru n<2, la fel ca în cazul anterior, egalitatea de mai jos nu poate fi adevărată pentru că unul din termeni este pozitiv, iar celălalt este negativ :
Pentru n=1, ecuația
Putem așadar, concluziona că pentru
ecuația
Dar dacă ecuația ar admite soluții reale negative,
separându-le de o parte și de alta a egalității,
sau înmulțind termenii cu (-1) în cazul în care toți termenii sunt negativi,
se ajunge la o ecuație cu termeni pozitivi, ca în cazul de mai sus.
În concluzie, putem generaliza că pentru
ecuația
Curi_osul- Mulţumit de forum : Numarul mesajelor : 7




Puncte : 12822
Data de inscriere : 22/03/2013
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Vreau să mai adaug o mică corectare pentru mesajul anterior și o completare pentru concluzia finală.
Se pleacă deci, de la egalitatea care trebuie îndeplinită într-un triunghi,
dacă între laturile x, y, z ale acestuia este adevărată egalitatea :
:
![\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]=y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]=y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]})
Pentru oricare x, y, z, n reale pozitive, ca și laturi ale unui triunghi, pentru relația de mai sus putem stabili condițiile și concluziile :
Dacă
\Rightarrow \begin{cases} & \text{ } \mathbf{\frac{z^2+x^2-y^2}{2\cdot x\cdot z}= \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}} \\ & \text{ } \\ & \text{ } \mathbf{\frac{z^2+y^2-x^2}{2\cdot y\cdot z}= \frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}} \end{cases})
de unde rezultă că pentru cazul n=2 este posibilă egalitatea :
![\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]=y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]=y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]})
Dacă
\Rightarrow }\begin{cases} & \text{ } \mathbf{\frac{z^2+x^2-y^2}{2\cdot x\cdot z}> \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}} \\ & \text{ } \\ & \text{ } \mathbf{\frac{z^2+y^2-x^2}{2\cdot y\cdot z}> \frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}} \end{cases})
de unde rezultă că pentru n< 2, egalitatea de mai jos nu poate fi adevărată pentru că unul din termeni este pozitiv, iar celălalt este negativ :
![\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]\neq y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]\neq y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]})
Dacă
\Rightarrow }\begin{cases} & \text{ } \mathbf{\frac{z^2+x^2-y^2}{2\cdot x\cdot z}< \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}} \\ & \text{ } \\ & \text{ } \mathbf{\frac{z^2+y^2-x^2}{2\cdot y\cdot z}< \frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}} \end{cases})
de unde rezultă că pentru n>2, la fel ca în cazul anterior, egalitatea de mai jos nu poate fi adevărată pentru că unul din termeni este pozitiv, iar celălalt este negativ :
![\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]\neq y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{x\cdot\left [ \frac{z^2+x^2-y^2}{2\cdot x\cdot z}- \frac{z^n+x^n-y^n}{2\cdot x\cdot z^{n-1}}\right ]\neq y\cdot\left [\frac{z^n+y^n-x^n}{2\cdot y\cdot z^{n-1}}- \frac{z^2+y^2-x^2}{2\cdot y\cdot z} \right ]})
Pentru n=1, ecuația are soluții reale pozitive, deși x, y, z nu pot fi laturile unui triunghi.
are soluții reale pozitive, deși x, y, z nu pot fi laturile unui triunghi.
Putem așadar, concluziona până aici că pentru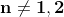
ecuația nu are soluții reale pozitive x, y, z, n.
nu are soluții reale pozitive x, y, z, n.
Dacă ecuația are exponentul negativ, aceasta se reduce tot la o ecuație cu exponenți pozitivi,
ai cărei termeni pot fi de asemenea, relaționați cu laturile unui triunghi :


^n}=\frac{1}{z^n} })
^n})
În acest caz, laturile triunghiului sunt , caz în care este valabil raționamentul pentru n pozitiv.
, caz în care este valabil raționamentul pentru n pozitiv.
Dacă ecuația ar admite soluții x, y, z reale negative,
separându-le de o parte și de alta a egalității,
sau înmulțind termenii cu (-1) în cazul în care toți termenii sunt negativi,
se ajunge la o ecuație cu termeni pozitivi, ca în cazul de mai sus.
Deci generalizat, pentru
ecuația nu are soluții reale x, y, z, n.
nu are soluții reale x, y, z, n.
Se pleacă deci, de la egalitatea care trebuie îndeplinită într-un triunghi,
dacă între laturile x, y, z ale acestuia este adevărată egalitatea
Pentru oricare x, y, z, n reale pozitive, ca și laturi ale unui triunghi, pentru relația de mai sus putem stabili condițiile și concluziile :
Dacă
de unde rezultă că pentru cazul n=2 este posibilă egalitatea :
Dacă
de unde rezultă că pentru n< 2, egalitatea de mai jos nu poate fi adevărată pentru că unul din termeni este pozitiv, iar celălalt este negativ :
Dacă
de unde rezultă că pentru n>2, la fel ca în cazul anterior, egalitatea de mai jos nu poate fi adevărată pentru că unul din termeni este pozitiv, iar celălalt este negativ :
Pentru n=1, ecuația
Putem așadar, concluziona până aici că pentru
ecuația
Dacă ecuația are exponentul negativ, aceasta se reduce tot la o ecuație cu exponenți pozitivi,
ai cărei termeni pot fi de asemenea, relaționați cu laturile unui triunghi :
În acest caz, laturile triunghiului sunt
Dacă ecuația ar admite soluții x, y, z reale negative,
separându-le de o parte și de alta a egalității,
sau înmulțind termenii cu (-1) în cazul în care toți termenii sunt negativi,
se ajunge la o ecuație cu termeni pozitivi, ca în cazul de mai sus.
Deci generalizat, pentru
ecuația
Curi_osul- Mulţumit de forum : Numarul mesajelor : 7




Puncte : 12822
Data de inscriere : 22/03/2013
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Curi_osul,
Repet:
O demonstraţie corectă trebuie facută obligatoriu pe baza celor două cazuri 1. şi 2. concepute de mine.De ce ai eliminat cazul 2.?
--------------------------------------
Nu am analizat încă ce-ai scris din lipsă de timp....şi sper să nu fi greşit raţionamentul iarăşi şi nici calculele bazate pe raţionamentul meu.
--------------------------------------------------
Am impresia că nu ai înteles clar ce concluzie rezultă din cazul 1. şi când am să-ţi spun ai să vezi cât de mult greşesti că iei în considerare doar acest caz 1. conceput de mine şi care caz presupune de fapt rezolvarea unei identităţi.Cazul 2. conceput de mine este de fapt rezolvarea unei ecuaţii diofantice şi care s-ar putea ca această ecuaţie diofantică să fie de fapt demonstrarea corectă a Marii Teoreme a lui Fermat.
Nu te grăbi şi mai anlizează ce am conceput eu!Nu transmite nicăieri demonstraţia aşa cum crezi tu ca să nu te faci cumva de râs!
Repet:
O demonstraţie corectă trebuie facută obligatoriu pe baza celor două cazuri 1. şi 2. concepute de mine.De ce ai eliminat cazul 2.?
--------------------------------------
Nu am analizat încă ce-ai scris din lipsă de timp....şi sper să nu fi greşit raţionamentul iarăşi şi nici calculele bazate pe raţionamentul meu.
--------------------------------------------------
Am impresia că nu ai înteles clar ce concluzie rezultă din cazul 1. şi când am să-ţi spun ai să vezi cât de mult greşesti că iei în considerare doar acest caz 1. conceput de mine şi care caz presupune de fapt rezolvarea unei identităţi.Cazul 2. conceput de mine este de fapt rezolvarea unei ecuaţii diofantice şi care s-ar putea ca această ecuaţie diofantică să fie de fapt demonstrarea corectă a Marii Teoreme a lui Fermat.
Nu te grăbi şi mai anlizează ce am conceput eu!Nu transmite nicăieri demonstraţia aşa cum crezi tu ca să nu te faci cumva de râs!
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22433
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
De ris ne facem toti noi ca, perdem timpul in zadar pe netu asta..Dacu a scris:Curi_osul,
Repet:
O demonstraţie corectă trebuie facută obligatoriu pe baza celor două cazuri 1. şi 2. concepute de mine.De ce ai eliminat cazul 2.?
--------------------------------------
Nu am analizat încă ce-ai scris din lipsă de timp....şi sper să nu fi greşit raţionamentul iarăşi şi nici calculele bazate pe raţionamentul meu.
--------------------------------------------------
Am impresia că nu ai înteles clar ce concluzie rezultă din cazul 1. şi când am să-ţi spun ai să vezi cât de mult greşesti că iei în considerare doar acest caz 1. conceput de mine şi care caz presupune de fapt rezolvarea unei identităţi.Cazul 2. conceput de mine este de fapt rezolvarea unei ecuaţii diofantice şi care s-ar putea ca această ecuaţie diofantică să fie de fapt demonstrarea corectă a Marii Teoreme a lui Fermat.
Nu te grăbi şi mai anlizează ce am conceput eu!Nu transmite nicăieri demonstraţia aşa cum crezi tu ca să nu te faci cumva de râs!
mai facem "cercetari",
Ideea ca x,y,z trebue sa fie laturile unui triunghi, din cite am zarit prin net, a fost inceputa de un utilizator chiar fiind mai demult pe acest forum, unul Joben am uitat numele si prenumele.
Si nu e de tine inceputa Dacule, termina cu minciunile, ca parca esti "credincios".
A doua la mina, voi se pare ca considerati caci si in cazul x^n,y^n,z^n tot trebue sa avem un triunghi,
de unde ati luat-o, unde e demonstratia [cit de simpla/evidenta nu ar fi pentru voi] ?!
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Precis ca nu poate fi x^n, y^n, z^n triunghi (deoarece indata contrazice egalitatea din enuntul ipotezei), chiar daca x,y,z trebue sa fie triunghi.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Dacule,
părerea mea este că nu ai nevoie de cazuri.
Pentru că aduci ecuația la o exprimare ce permite compararea cu o relație identică ca exprimare, dar despre care știm că e adevărată.
N-ai nevoie de cazuri.
Dar nici raționamentul pe care l-am scris mai sus nu este suficient,
deși concluziile sunt logice.
meteor,
noi analizăm aici ca laturi ale unui triunghi,
valorile x, y și z,
nu x^n, y^n și z^n,
despre care încercăm să stabilim că pentru n diferit de 2,
între laturile triunghiului nu poate exista egalitatea x^n+y^n=z^n.
Repet, părerea mea este că nu ai nevoie de cazuri, Dacule.
Și nu spun asta doar de dragul de a te contrazice,
ci pentru că așa văd eu logic problema în stadiul în care se află,
dar mai trebuie completat ceva în raționament.
Acum fie că este nevoie de cazuri, fie că nu este,
important pentru mine este ca această relaționare cu laturile triunghiului să poată fi considerată un raționament solid și eficient,
în analiza acestei teoreme.
Rușinea la care m-aș expune nu mai reprezintă pentru mine o problemă.
Rușine ar fi ca toți cei în măsură să valideze o asemenea demonstrație, să nu o facă doar pentru că ar fi un raționament prea simplu pentru o problemă care nu s-a putut demonstra atâta timp și de atâția matematicieni.
Mă îndoiesc totuși, că niciunul din marii matematicieni, nu a analizat problema în acest mod și să ajungă la aceste concluzii.
Sunt foarte curios să aflu motivul pentru care acest tip de raționament nu poate fi considerat corect.
Tu fă-i Dacule câte cazuri consideri necesare.
Eu am nevoie doar de unul sau mai multe argumente pentru care logica raționamentului pe care l-am folosit (preluat și prelucrat de la tine) nu este corect și nu poate valida logic demonstrația.
Acum, mai degrabă mă lupt cu logica și încerc să găsesc argumente pentru care raționamentul nu poate fi corect.
Oricum, chiar și în ce am scris mai sus,
doar ideea de bază este interesantă,
însă din punct de vedere elementar demonstrația nu este competă.
În al doilea și al treilea mesaj, de asemenea sunt greșeli pe care nu le-ai observat.
Tu mai degrabă te concentrezi la versiunea ta.
Mult succes.
Eu încă mai caut simplificarea la maxim, dar care să fie suficient pentru a trage concluziile, a raționamentului demonstrației.
Și nu din concurență cu tine, ci pentru mine însumi.
părerea mea este că nu ai nevoie de cazuri.
Pentru că aduci ecuația la o exprimare ce permite compararea cu o relație identică ca exprimare, dar despre care știm că e adevărată.
N-ai nevoie de cazuri.
Dar nici raționamentul pe care l-am scris mai sus nu este suficient,
deși concluziile sunt logice.
meteor,
noi analizăm aici ca laturi ale unui triunghi,
valorile x, y și z,
nu x^n, y^n și z^n,
despre care încercăm să stabilim că pentru n diferit de 2,
între laturile triunghiului nu poate exista egalitatea x^n+y^n=z^n.
Repet, părerea mea este că nu ai nevoie de cazuri, Dacule.
Și nu spun asta doar de dragul de a te contrazice,
ci pentru că așa văd eu logic problema în stadiul în care se află,
dar mai trebuie completat ceva în raționament.
Acum fie că este nevoie de cazuri, fie că nu este,
important pentru mine este ca această relaționare cu laturile triunghiului să poată fi considerată un raționament solid și eficient,
în analiza acestei teoreme.
Rușinea la care m-aș expune nu mai reprezintă pentru mine o problemă.
Rușine ar fi ca toți cei în măsură să valideze o asemenea demonstrație, să nu o facă doar pentru că ar fi un raționament prea simplu pentru o problemă care nu s-a putut demonstra atâta timp și de atâția matematicieni.
Mă îndoiesc totuși, că niciunul din marii matematicieni, nu a analizat problema în acest mod și să ajungă la aceste concluzii.
Sunt foarte curios să aflu motivul pentru care acest tip de raționament nu poate fi considerat corect.
Tu fă-i Dacule câte cazuri consideri necesare.
Eu am nevoie doar de unul sau mai multe argumente pentru care logica raționamentului pe care l-am folosit (preluat și prelucrat de la tine) nu este corect și nu poate valida logic demonstrația.
Acum, mai degrabă mă lupt cu logica și încerc să găsesc argumente pentru care raționamentul nu poate fi corect.
Oricum, chiar și în ce am scris mai sus,
doar ideea de bază este interesantă,
însă din punct de vedere elementar demonstrația nu este competă.
În al doilea și al treilea mesaj, de asemenea sunt greșeli pe care nu le-ai observat.
Tu mai degrabă te concentrezi la versiunea ta.
Mult succes.
Eu încă mai caut simplificarea la maxim, dar care să fie suficient pentru a trage concluziile, a raționamentului demonstrației.
Și nu din concurență cu tine, ci pentru mine însumi.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Înainte de a afirma că eu sunt un mincinos ar trebui să vii cu dovada clară că acel "Joben" a spus ceea ce şi eu am spus.Chiar şi dăcă ar fi aşa nu văd de ce separat faţă de "Joben" am ajuns şi eu la aceiaşi concluzie.Bolyai şi Lobacevski şi se pare că şi Gauss s-au gândit la conceperea unei geometrii neeuclidiene.Eu nu fur nicio idee de la nimeni şi sunt convins că idea mea de raţionament în demonstrarea Marii Teoreme a lui Fermat ar putea fi greşită şi tocmai de aceea îi spuneam şi lui curiosul alias Curi-osul să nu se grăbească a crede că a rezolvat această teoremă.Dacă ai ceva de obiectat privind raţionamentul meu atunci obiectează şi nu arunca cu pietre în mine!Aştept dovada privind acel "Joben"!meteor a scris:Dacu a scris:Curi_osul,
Repet:
O demonstraţie corectă trebuie facută obligatoriu pe baza celor două cazuri 1. şi 2. concepute de mine.De ce ai eliminat cazul 2.?
--------------------------------------
Nu am analizat încă ce-ai scris din lipsă de timp....şi sper să nu fi greşit raţionamentul iarăşi şi nici calculele bazate pe raţionamentul meu.
--------------------------------------------------
Am impresia că nu ai înteles clar ce concluzie rezultă din cazul 1. şi când am să-ţi spun ai să vezi cât de mult greşesti că iei în considerare doar acest caz 1. conceput de mine şi care caz presupune de fapt rezolvarea unei identităţi.Cazul 2. conceput de mine este de fapt rezolvarea unei ecuaţii diofantice şi care s-ar putea ca această ecuaţie diofantică să fie de fapt demonstrarea corectă a Marii Teoreme a lui Fermat.
Nu te grăbi şi mai anlizează ce am conceput eu!Nu transmite nicăieri demonstraţia aşa cum crezi tu ca să nu te faci cumva de râs!
Ideea ca x,y,z trebue sa fie laturile unui triunghi, din cite am zarit prin net, a fost inceputa de un utilizator chiar fiind mai demult pe acest forum, unul Joben am uitat numele si prenumele.
Si nu e de tine inceputa Dacule, termina cu minciunile, ca parca esti "credincios".
A doua la mina, voi se pare ca considerati caci si in cazul x^n,y^n,z^n tot trebue sa avem un triunghi,
de unde ati luat-o, unde e demonstratia [cit de simpla/evidenta nu ar fi pentru voi] ?!
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22433
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
curiosul,
Sper ca azi să-ţi arăt că este greşit să elimini cazul 2. conceput de mine precum şi faptul că este greşit să tragi concluzia că este suficient a analiza doar cazul 1. conceput de mine.
Tu nu ai cum să vezi încă deficienţa considerării numai a cazului 1. conceput de mine în sensul că este incomplet analizat şi de fapt cred că si cazul 2. conceput tot de mine este incomplet analizat şi asta deoarece de fapt acel sistem de două ecuaţii este incomplet atât în cazul 1. cât şi în cazul 2. concepute de mine şi spunând aceste lucruri aproape cred că ţi-am şi sugerat o idee privind greşelile raţionamentului conceput de mine şi preluat de tine fără o analiză corespunzătoare şi profesionistă.Repet,am un alt raţionament de demonstrare a Marii Teoreme a lui Fermat dar pe care nu l-am finalizat încă.....Nu te grăbi!Graba strică treaba!Ne mai învârtim!
Demonstraţia mea dacă este bună atunci meritul este doar al lui Dumnezeu căci eu nu am niciun merit!Daca raţionamentul demonstraţiei mele este greşit (şi înclin să cred tot mai mult că este aşa) atunci eu am fost dus în ispita de a greşi cu voia lui Dumnezeu.

Sper ca azi să-ţi arăt că este greşit să elimini cazul 2. conceput de mine precum şi faptul că este greşit să tragi concluzia că este suficient a analiza doar cazul 1. conceput de mine.
Tu nu ai cum să vezi încă deficienţa considerării numai a cazului 1. conceput de mine în sensul că este incomplet analizat şi de fapt cred că si cazul 2. conceput tot de mine este incomplet analizat şi asta deoarece de fapt acel sistem de două ecuaţii este incomplet atât în cazul 1. cât şi în cazul 2. concepute de mine şi spunând aceste lucruri aproape cred că ţi-am şi sugerat o idee privind greşelile raţionamentului conceput de mine şi preluat de tine fără o analiză corespunzătoare şi profesionistă.Repet,am un alt raţionament de demonstrare a Marii Teoreme a lui Fermat dar pe care nu l-am finalizat încă.....Nu te grăbi!Graba strică treaba!Ne mai învârtim!
Demonstraţia mea dacă este bună atunci meritul este doar al lui Dumnezeu căci eu nu am niciun merit!Daca raţionamentul demonstraţiei mele este greşit (şi înclin să cred tot mai mult că este aşa) atunci eu am fost dus în ispita de a greşi cu voia lui Dumnezeu.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22433
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Chiar te rog .
De fapt chiar asta îmi doresc.
Ca să mă analizez să văd unde sunt scăpările de logică.
Nu-i nicio supărare, dă-i tare.
Renunță la a mai folosi :
"...tot principiul gândit de mine...
...cazul x conceput de mine..."
pentru că știe deja toată lumea că acesta este raționamentul tău.
Nu trebuie să-i mai convingi de asta.
Aștept să-mi explici necesitatea cazurilor (concepute și gândite de tine).
Eu înțeleg ce vrei să spui, dar cred că și cazurile respective sunt ineficiente, așa cum este și raționamentul pe care am încercat (incomplet) să-l simplific.
Sigur, cu siguranță ne mai învârtim pe aici.
Problema ( printr-o demonstrație elementară) nu este nici pe departe terminată.
De fapt chiar asta îmi doresc.
Ca să mă analizez să văd unde sunt scăpările de logică.
Nu-i nicio supărare, dă-i tare.
Renunță la a mai folosi :
"...tot principiul gândit de mine...
...cazul x conceput de mine..."
pentru că știe deja toată lumea că acesta este raționamentul tău.
Nu trebuie să-i mai convingi de asta.
Aștept să-mi explici necesitatea cazurilor (concepute și gândite de tine).
Eu înțeleg ce vrei să spui, dar cred că și cazurile respective sunt ineficiente, așa cum este și raționamentul pe care am încercat (incomplet) să-l simplific.
Sigur, cu siguranță ne mai învârtim pe aici.
Problema ( printr-o demonstrație elementară) nu este nici pe departe terminată.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
https://cercetare.forumgratuit.ro/t13-marea-teorema-a-lui-fermat?highlight=Fermat
Eu nu sunt sigur daca e ok sa incepeti a analiza problema pornind de la sistemul:
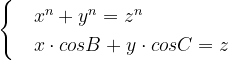
Mai sigur cred ca e daca se analizeaza sistemul:

De fapt inegalitatile din sistem rezulta imediat din egalitate.
@Dacu, nu te mai pune atit alaturi de Gauss, Lobacevski, Boljai, etc. , ca nu ai facut pina ce inca nimic concret in matematica.
, ca nu ai facut pina ce inca nimic concret in matematica.
Eu nu sunt sigur daca e ok sa incepeti a analiza problema pornind de la sistemul:
Mai sigur cred ca e daca se analizeaza sistemul:
De fapt inegalitatile din sistem rezulta imediat din egalitate.
@Dacu, nu te mai pune atit alaturi de Gauss, Lobacevski, Boljai, etc.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25846
Data de inscriere : 19/06/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Nu renunţ la ceea ce Dumnezeu a dorit ca eu să spun!Atât în cazul 1. cât şi în cazul 2. concepute de mine sistemul de ecuaţii aare mai multe ecuaţii şi nu aşa cum am considerat eu iar tu ai preluat ideea mea precum şi raţionamentul fără să vezi eroarea aceasta.Ei bine sistemul de ecuaţi nu este format numai din două ecuaţii ci din mai multe ecuaţii şi ca atare rezultă şi alte cazuri care trebuie analizate pentru a fisiguri că nu existăcuriosul a scris:Chiar te rog .
De fapt chiar asta îmi doresc.
Ca să mă analizez să văd unde sunt scăpările de logică.
Nu-i nicio supărare, dă-i tare.
Renunță la a mai folosi :
"...tot principiul gândit de mine...
...cazul x conceput de mine..."
pentru că știe deja toată lumea că acesta este raționamentul tău.
Nu trebuie să-i mai convingi de asta.
Aștept să-mi explici necesitatea cazurilor (concepute și gândite de tine).
Eu înțeleg ce vrei să spui, dar cred că și cazurile respective sunt ineficiente, așa cum este și raționamentul pe care am încercat (incomplet) să-l simplific.
Sigur, cu siguranță ne mai învârtim pe aici.
Problema ( printr-o demonstrație elementară) nu este nici pe departe terminată.
Ultima editare efectuata de catre Dacu in Lun 25 Mar 2013, 17:39, editata de 2 ori
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22433
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Eu sunt un umil pasionat de matematică şi nu mă pun alături de nicun profesor de matematică de liceu darămite de marii matematicieni ai lumii.Nu văd ce a demonstrat acel "Joben".meteor a scris:https://cercetare.forumgratuit.ro/t13-marea-teorema-a-lui-fermat?highlight=Fermat
Eu nu sunt sigur daca e ok sa incepeti a analiza problema pornind de la sistemul:
Mai sigur cred ca e daca se analizeaza sistemul:
De fapt inegalitatile din sistem rezulta imediat din egalitate.
@Dacu, nu te mai pune atit alaturi de Gauss, Lobacevski, Boljai, etc., ca nu ai facut pina ce inca nimic concret in matematica.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22433
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Dacu a scris:
Dacă promiţi că nu mai preiei ideile mele ca să ţi le însuşeşti ...,atunci voi arăta sistemul de ecuaţii ,zic eu, complet pentru o analiză ulterioară...Nu este bine aşa!!!Nu te mai grăbi!!!
Ai dreptate !
Asta este problema mea, că mă grăbesc și sunt agitat tot timpul.
Acum, după mult mai multe analize, îmi dau seama că nu este deloc completă.
Ideea de bază este bună, dar insuficientă.
Cel puțin pentru moment.
Când am vrut să-mi însușesc ceva pe numele meu, raționamentul folosit nu avea nicio legătură cu triunghiul sau cu sistemul tău de ecuații.
Dar s-a dovedit a fi greșit, nu însușit.
Dacă vrei să scrii, scrie, cei ce vor citi vor știi că ăla este meritul tău, nu trebuie să-ți fie teamă că-ți fură cineva ceva.
De fapt Dacule, asta este teama multora dintre noi, că altul se va folosi și va câștiga de pe urma meritelor noastre.
Dacă am încerca să colaborăm prietenește, fără să ne gândim la merite și la câștiguri, cred că ar fi un mod de lucru mai eficient.
Noi ne-am războit în merite pentru ceva greșit și incomplet.
Să ne fie rușine la amândoi, aș zice.
Oricum, dacă scrii ceva, o să încerc să fiu mai liniștit și să încerc să-mi argumentez bine și corect obiecțiile, dacă sunt, bineînțeles.
Sau poate că iar îmi vine vreo sclipire plecând de la ce vei scrie tu, caz în care vreau să fii conștient că nu-ți însușesc nimic.
Mi-a ajuns. Mi-a trecut dorința de celebritate
Hai să ne concentrăm la ceva ce poate aduce rezultate.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
De ce s-ă-mi fie mie ruşine???curiosul a scris:
Să ne fie rușine la amândoi, aș zice.
Hai să ne concentrăm la ceva ce poate aduce rezultate.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22433
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Ca să ne apropiem o idee mai mult de completarea demonstrației,
ar fi folositoare o demonstrație care arată că dacă un triunghi nu este dreptunghic,
atunci nu pot fi adevărate simultan relațiile din sistemul
 , sau din sistemul
, sau din sistemul 
Dacă triunghiul nu este dreptunghic,
fie , fie
, fie 
Crezi că este adevărată presupunerea Dacule ?
Dacă da cum am putea-o demonstra ?
ar fi folositoare o demonstrație care arată că dacă un triunghi nu este dreptunghic,
atunci nu pot fi adevărate simultan relațiile din sistemul
Dacă triunghiul nu este dreptunghic,
fie
Crezi că este adevărată presupunerea Dacule ?
Dacă da cum am putea-o demonstra ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
curiosul,
Promite-mi că nu mai ştergi mesajele tale şi nu le mai modifici fără să faci referire expresă că ai modificat conform indicaţiei mele sau a unui alt forumist şi să-mi promiţi că nu mai preiei ideile mele sau ale altora fără a specifica clar ale cui sunt!Deasemeni promite-mi că nu vei şterge sau modifica (ca moderator sau altceva) ideile mele sau ale altora din mesajele respective!
-----------------------------------------------------------------------------------------
Nu văd ce rost au acele inegalităţi fără a specifica clar cât de mari pot fi unghiurile mai ales că am stabilit între laturile triunghiului relaţia de ordine
mai ales că am stabilit între laturile triunghiului relaţia de ordine  .În primul rând este absolut necesar ca pentru
.În primul rând este absolut necesar ca pentru  triunghiul să aibă toate unghiurile mai mici ca
triunghiul să aibă toate unghiurile mai mici ca  şi asta se arată foarte uşor.
şi asta se arată foarte uşor.
Cât de mari şi cât de mici pot fi unghiurile triunghiului în cazul în care ?Se poate arăta foarte uşor care sunt valorile posibile ale acestor unghiuri ştiind că latura
?Se poate arăta foarte uşor care sunt valorile posibile ale acestor unghiuri ştiind că latura  este opusă
este opusă  , latura
, latura  este opusă
este opusă  şi respectiv latura
şi respectiv latura  este opusă
este opusă  .Eu zic că
.Eu zic că  şi deci
şi deci  .
.
Se arată deasemeni foarte uşor următoarele inegalităţi:



 .
.

Promite-mi că nu mai ştergi mesajele tale şi nu le mai modifici fără să faci referire expresă că ai modificat conform indicaţiei mele sau a unui alt forumist şi să-mi promiţi că nu mai preiei ideile mele sau ale altora fără a specifica clar ale cui sunt!Deasemeni promite-mi că nu vei şterge sau modifica (ca moderator sau altceva) ideile mele sau ale altora din mesajele respective!
-----------------------------------------------------------------------------------------
Nu văd ce rost au acele inegalităţi fără a specifica clar cât de mari pot fi unghiurile
Cât de mari şi cât de mici pot fi unghiurile triunghiului în cazul în care
Se arată deasemeni foarte uşor următoarele inegalităţi:
Ultima editare efectuata de catre Dacu in Mar 26 Mar 2013, 09:27, editata de 3 ori
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22433
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Dacu a scris:Nu văd ce rost au acele inegalităţi ...
Oricum se pare că presupunerea este greșită, dar ar fi fost folositoare pentru a arăta că dacă ambele relații sunt adevărate în sistemul :
atunci
dacă într-un triunghi care nu este dreptunghic sunt adevărate ambele relații într-unul din sistemele :
Pentru că exprimi atât
în funcție de
Pentru că dacă n>2 atunci sunt adevărate simultan ambele relații din sistemul
În timp ce, dacă triunghiul nu este dreptunghic atunci
Am ajunge deja într-o situație în care am putea stabili cu certitudine că ambele relații din sistemul
sunt adevărate doar dacă
pentru că
Și te-aș ruga să începi să renunți la exprimările tale referitoare la faptul că mi-am însușit ceva și că am șters ceva, pentru că motivul pentru care folosești menționarea lor este doar de a sublinia valoarea ta prin instabilitatea și fragilitatea mea, nu te deranjează pe tine faptul că cititorii nu mai înțeleg nimic.
Dacă vrei să ne concentrăm la dezvoltarea unui raționament corect și complet ne mai jucăm, dacă nu, nu.
Să uităm ce-a fost și să ne focusăm la ce avem de făcut.
Lasă meritele și valoarea ta.
Că deocamdată nu este nimic bine și solid pus la punct, ca să fii îndreptățit să crezi că cineva ți-a furat ceva de valoare sau că cineva ar fi mai bun ca tine.
Te consumi pentru lucruri care nu au deocamdată un suport real valoros.
Deci dacă ai înțeles de ce consider necesar ce am afirmat în mesajul anterior,
crezi că am putea demonstra asta ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
curiosul alias Curi-osul,
Faptul că tu nu poţi sau nu vrei să fii corect şi mai ales faptul că tu ai o problemă de sănătate (hiperexcitabilitate neuronală) mă fac pe mine să iau hotărârea de a ignora de-acum încolo toate mesajele tale de orice fel.
Îţi doresc multă sănatate şi toate cele bune!Dumnezeu să te binecuvânteze!
Faptul că tu nu poţi sau nu vrei să fii corect şi mai ales faptul că tu ai o problemă de sănătate (hiperexcitabilitate neuronală) mă fac pe mine să iau hotărârea de a ignora de-acum încolo toate mesajele tale de orice fel.
Îţi doresc multă sănatate şi toate cele bune!Dumnezeu să te binecuvânteze!
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22433
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
OK, te înțeleg .
Nu-i nicio problemă.
Toate bune
Nu-i nicio problemă.
Toate bune
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Un raționament mai eficient și mai ușor de verificat, plecând tot de la sistemul lui Dacu, ar putea fi analiza de mai jos, în care am folosit în mare parte principiile gândite și concepute de el, cu mici completări :
Așadar, plecând de la sistemul construit de Dacu la nivelul unui triunghi ,
dacă între laturile x, y, z ale acestuia este adevărată egalitatea , ajungem la :
, ajungem la :

Înmulțim a doua relație cu și ajungem la :
și ajungem la :

=y\left ( y^{n-1}-z^{n-1}\cdot cosC \right )})
În continuare, notăm pentru simplificare

și analizăm separat ecuația .
.
Vom stabili în continuare că dacă y>x și , atunci (x+a)<(y+b) :
, atunci (x+a)<(y+b) :
<(y+b)} \end{cases})
<(y+b)} \end{cases}\Leftrightarrow \begin{cases} \mathbf{a=\frac{y\cdot b}{x}} \\ \mathbf{(x+\frac{y\cdot b}{x})<(y+b)} \end{cases}\Leftrightarrow)

<y(x-b)} \end{cases}\Leftrightarrow \begin{cases} \mathbf{a=\frac{y\cdot b}{x}} \\ \mathbf{x<y} \end{cases})
Deci, dacă y>x și , atunci ambele relații din sistemul de mai jos sunt simultan adevărate :
, atunci ambele relații din sistemul de mai jos sunt simultan adevărate :

Din ultimul sistem rezultă că}) și că
și că  .
.
Dacă ambele relații din ultimul sistem de mai sus sunt adevărate, înseamnă că trebuie să fie adevărată și inegalitatea :
})
})
})
<x\cdot (y-x)\Rightarrow {\color{DarkBlue} b<x}})
De aici rezultă că



})
})
})
Prin raționamentul pe care l-a folosit Dacu, se poate arăta ușor că pentru n suficient de mare ( mai mare ca 4) sensul inegalității de mai sus este de fapt invers, iar
})
Aceasta înseamnă că adevărul inegalității de mai sus contrazice una din relațiile sistemului :

Pentru că y>x este o relație adevărată, rezultă că pentru valorile lui n pentru care
})
relația nu este adevărată.
nu este adevărată.
Dacă aceasta nu este adevărată, înlocuind a și b ajungem la a stabili că pentru acele valori ale lui n ,
nu este adevărată egalitatea
Pentru moment nu sunt capabil să găsesc demonstrațiile cazurilor n=3,4,5.
Intervențiile lui Dacu ar fi binevenite.
Nu mai scriu acum în LaTex, însă este suficientă și o demonstrație pentru faptul că dacă n>2, atunci

în cazul în care cineva are vreo idee.
Așadar, plecând de la sistemul construit de Dacu la nivelul unui triunghi ,
dacă între laturile x, y, z ale acestuia este adevărată egalitatea
Înmulțim a doua relație cu
În continuare, notăm pentru simplificare
și analizăm separat ecuația
Vom stabili în continuare că dacă y>x și
Deci, dacă y>x și
Din ultimul sistem rezultă că
Dacă ambele relații din ultimul sistem de mai sus sunt adevărate, înseamnă că trebuie să fie adevărată și inegalitatea :
De aici rezultă că
Prin raționamentul pe care l-a folosit Dacu, se poate arăta ușor că pentru n suficient de mare ( mai mare ca 4) sensul inegalității de mai sus este de fapt invers, iar
Aceasta înseamnă că adevărul inegalității de mai sus contrazice una din relațiile sistemului :
Pentru că y>x este o relație adevărată, rezultă că pentru valorile lui n pentru care
relația
Dacă aceasta nu este adevărată, înlocuind a și b ajungem la a stabili că pentru acele valori ale lui n ,
nu este adevărată egalitatea
Pentru moment nu sunt capabil să găsesc demonstrațiile cazurilor n=3,4,5.
Intervențiile lui Dacu ar fi binevenite.
Nu mai scriu acum în LaTex, însă este suficientă și o demonstrație pentru faptul că dacă n>2, atunci
în cazul în care cineva are vreo idee.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Ori există o incoerență sau vreo greșeală pe undeva, ori analiza de mai jos este o variantă mai bună .
Deci, dacă între laturile unui triunghi este adevărată egalitatea , ajungem la egalitatea
, ajungem la egalitatea
![\dpi{150} \mathbf{x\cdot \left [ cosB-\frac{x^{n-1}}{z^{n-1}} \right ]=y\cdot \left [\frac{y^{n-1}}{z^{n-1}}-cosC \right ]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{x\cdot \left [ cosB-\frac{x^{n-1}}{z^{n-1}} \right ]=y\cdot \left [\frac{y^{n-1}}{z^{n-1}}-cosC \right ]})
Notând pentru simplificare

ajungem să arătăm că dacă y>x și , atunci
, atunci
%3C(y+b)}%20\end{cases})
(Demonstrația este în mesajul anterior)
Dacă în ultimul sistem sunt adevărate ambele relații și înmulțind cu ab ultima relație, obținem :

<ab( b-a)})
b-(yb)a<ab( b-a)})
Pentru că considerăm adevărată prima relație al celui de-al doilea sistem atunci notăm xa=yb=q și înlocuim în inegalitatea de mai sus:
})
<ab( b-a)\Rightarrow q<ab})
Înlocuind necunoscutele ajungem la sistemul de mai jos, în care ambele relații trebuie să fie adevărate :

Ambele inegalități din sistemul de mai sus sunt false , pentru că cei doi termeni din dreapta inegalităților sunt subunitari.
Aceasta contrazice una din relațiile sistemului
%3C(y+b)}%20\end{cases})
și indirect egalitatea
E pe undeva vreo greșeală, Dacule ?
Deci, dacă între laturile unui triunghi este adevărată egalitatea
Notând pentru simplificare
ajungem să arătăm că dacă y>x și
(Demonstrația este în mesajul anterior)
Dacă în ultimul sistem sunt adevărate ambele relații și înmulțind cu ab ultima relație, obținem :
Pentru că considerăm adevărată prima relație al celui de-al doilea sistem atunci notăm xa=yb=q și înlocuim în inegalitatea de mai sus:
Înlocuind necunoscutele ajungem la sistemul de mai jos, în care ambele relații trebuie să fie adevărate :
Ambele inegalități din sistemul de mai sus sunt false , pentru că cei doi termeni din dreapta inegalităților sunt subunitari.
Aceasta contrazice una din relațiile sistemului
și indirect egalitatea
E pe undeva vreo greșeală, Dacule ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
curiosul a scris:
Deci, dacă între laturile unui triunghi este adevărată egalitatea, ajungem la egalitatea
Notând pentru simplificare
ajungem să arătăm că dacă y>x și, atunci
(Demonstrația este în mesajul anterior)
Dacă în ultimul sistem sunt adevărate ambele relații și înmulțind cu ab ultima relație, obținem :
Pentru că considerăm adevărată prima relație al celui de-al doilea sistem atunci notăm xa=yb=q și înlocuim în inegalitatea de mai sus:
Înlocuind necunoscutele ajungem la sistemul de mai jos, în care ambele relații trebuie să fie adevărate :
Ambele inegalități din sistemul de mai sus sunt false , pentru că cei doi termeni din dreapta inegalităților sunt subunitari.
De aici rezultă că ambele relații ale sistemelor
și implicit inegalitatea
sunt adevărate doar dacă
Aceasta este posibil doar dacă
iar
Aceste egalități sunt corecte doar pentru n=2.
Dacule,
repet, m-am folosit de sistemul tău, pe care am încercat să-l dezvolt încât raționamentul să fie corect.
Nu vreau să crezi că ți-am furat ceva, sau că mi-am însușit ceva al tău,
ci doar nu mi-am putut stăpâni tendința de dezvolta mai bine și mai corect cred eu,
ideea de bază a sistemului.
Te-aș ruga să-mi spui eventualele greșeli , pe care să încercăm să le corectăm
și să scriem odată pentru totdeauna demonstrația asta (elementară) completă și corectă.
Lasă problemele mele de sănătate și leagă-te doar de corectitudinea logică a raționamentelor.
Mulțumesc mult și te aștept.
Aici este vorba și de meritul tău și mi-aș dori mult să intervii.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Să punem raționamentul pus cap la cap într-un singur mesaj :
"Pentru n>2, ecuația nu are soluții întregi."
nu are soluții întregi."
Vom demonstra în continuare că pentru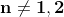 ecuația nu are soluții reale x, y, z, n.
ecuația nu are soluții reale x, y, z, n.
Stabilim în primul rând că valorile x, y, z trebuie să fie laturile unui triunghi.
Dacă ecuația are soluții, atunci (x+y)>z>y.
are soluții, atunci (x+y)>z>y.
Condiția (x+y)>z>y este îndeplinită de laturile x, y, z ale unui triunghi, cu z>y>x.
Deci soluțiile x, y, z ale ecuației pot fi considerate laturile unui triunghi.
pot fi considerate laturile unui triunghi.
Presupunem adevărată egalitatea între laturile unui triunghi și putem așadar, construi sistemul :
între laturile unui triunghi și putem așadar, construi sistemul :
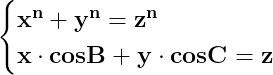
unde unghiurile B și C sunt unghiurile formate de laturile x și z, respectiv y și z.
Înmulțim cu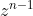 termenii celei de-a doua egalități a sistemului și ajungem la :
termenii celei de-a doua egalități a sistemului și ajungem la :
![\dpi{150} \mathbf{z^{n-1}\left [ x\cdot cosB+y\cdot cosC \right ]=z^n=x^n+y^n}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{z^{n-1}\left [ x\cdot cosB+y\cdot cosC \right ]=z^n=x^n+y^n})
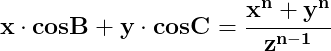
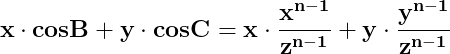
![\dpi{150} \mathbf{ x\cdot \left [ cosB-\frac{x^{n-1}}{z^{n-1}} \right ]=+y\cdot\left [ \frac{y^{n-1}}{z^{n-1}}- cosC\right ] }](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{ x\cdot \left [ cosB-\frac{x^{n-1}}{z^{n-1}} \right ]=+y\cdot\left [ \frac{y^{n-1}}{z^{n-1}}- cosC\right ] })
Notăm pentru simpificare
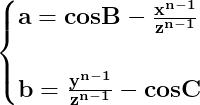
Vom arăta în continuare că dacă y>x și xa=yb, atunci

<y+b} \end{cases})
<y+b} \end{cases}\Leftrightarrow\begin{cases} \mathbf{a=\frac{y\cdot b}{x}} \\ \mathbf{\frac{x^2+y\cdot b}{x}<y+b} \end{cases})


<y(x-b)} \end{cases})
<y(x-b)} \end{cases}\Leftrightarrow\begin{cases} \mathbf{a=\frac{y\cdot b}{x}} \\ \mathbf{x<y} \end{cases})
Deci dacă într-un triunghi sunt adevărate relațiile din primul sistem de mai jos, sunt adevărate și relațiile din al doilea sistem de mai jos :

Dezvoltăm în continuare a doua relație a ultimului sistem :


<a b (b-a)})
 b-(y b) a <a b (b-a)})
Notăm termenii primei egalități din ultimul sistem cu
=(y b)=q})
și înlocuim în ultima inegalitate :
 b-(yb) a <a b (b-a)})
})
<a b (b-a)})
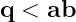
Înlocuind necunoscutele se ajunge ca ambele relații ale sistemelor trebuie să fie adevărate :

În ultimul sistem, termenii din dreapta inegalităților sunt subunitari, iar cei din stânga sunt supraunitari, ceea ce înseamnă că cele două inegalități sunt false.
Revenind la sistemul inițial

rezultă că ambele relații sunt adevărate doar dacă a=b=0, ceea ce înseamnă că
![\dpi{150} \mathbf{\left [ cosB-\frac{x^{n-1}}{z^{n-1}} \right ]= \left [ \frac{y^{n-1}}{z^{n-1}}-cosC \right ]=0} \\](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{\left [ cosB-\frac{x^{n-1}}{z^{n-1}} \right ]= \left [ \frac{y^{n-1}}{z^{n-1}}-cosC \right ]=0} \\)
precum și

Egalitățile de mai sus sunt adevărate doar pentru n=2.
Pentru că laturile x, y, z ale triunghiului pot fi considerate oricare numere reale
care îndeplinesc condițiile x+y>z , x+z>y și y+z>x,
putem afirma că pentru n diferit de 2,
între laturile unui triunghi nu poate fi adevărată egalitatea
și implicit ecuația respectivă nu are soluții reale pentru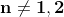 ,
,
deoarece pentru n=1, deși x+y=z, nu pot fi laturile unui triunghi, ecuația are soluții reale.
Observație
Analiza de mai sus este bazată pe observația utilizatorului Dacu, care a stabilit relația dintre laturile triunghiului și soluțiile ecuației din Marea teoremă a lui Fermat.
"Pentru n>2, ecuația
Vom demonstra în continuare că pentru
Stabilim în primul rând că valorile x, y, z trebuie să fie laturile unui triunghi.
Dacă ecuația
Condiția (x+y)>z>y este îndeplinită de laturile x, y, z ale unui triunghi, cu z>y>x.
Deci soluțiile x, y, z ale ecuației
Presupunem adevărată egalitatea
unde unghiurile B și C sunt unghiurile formate de laturile x și z, respectiv y și z.
Înmulțim cu
Notăm pentru simpificare
Vom arăta în continuare că dacă y>x și xa=yb, atunci
Deci dacă într-un triunghi sunt adevărate relațiile din primul sistem de mai jos, sunt adevărate și relațiile din al doilea sistem de mai jos :
Dezvoltăm în continuare a doua relație a ultimului sistem :
Notăm termenii primei egalități din ultimul sistem cu
și înlocuim în ultima inegalitate :
Înlocuind necunoscutele se ajunge ca ambele relații ale sistemelor trebuie să fie adevărate :
În ultimul sistem, termenii din dreapta inegalităților sunt subunitari, iar cei din stânga sunt supraunitari, ceea ce înseamnă că cele două inegalități sunt false.
Revenind la sistemul inițial
rezultă că ambele relații sunt adevărate doar dacă a=b=0, ceea ce înseamnă că
precum și
Egalitățile de mai sus sunt adevărate doar pentru n=2.
Pentru că laturile x, y, z ale triunghiului pot fi considerate oricare numere reale
care îndeplinesc condițiile x+y>z , x+z>y și y+z>x,
putem afirma că pentru n diferit de 2,
între laturile unui triunghi nu poate fi adevărată egalitatea
și implicit ecuația respectivă nu are soluții reale pentru
deoarece pentru n=1, deși x+y=z, nu pot fi laturile unui triunghi, ecuația are soluții reale.
Observație
Analiza de mai sus este bazată pe observația utilizatorului Dacu, care a stabilit relația dintre laturile triunghiului și soluțiile ecuației din Marea teoremă a lui Fermat.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Există o soluție și mai simplă !
Deci,
![\dpi{150} \mathbf{ x\cdot \left [ cosB-\frac{x^{n-1}}{z^{n-1}} \right ]=+y\cdot\left [ \frac{y^{n-1}}{z^{n-1}}- cosC\right ] }](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{ x\cdot \left [ cosB-\frac{x^{n-1}}{z^{n-1}} \right ]=+y\cdot\left [ \frac{y^{n-1}}{z^{n-1}}- cosC\right ] })
Notăm pentru simpificare
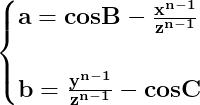
Am arătat în mesajul anterior că dacă y>x și xa=yb, atunci (y+b)>(x+a).
Dar dacă y>x, egalitatea xa=yb este adevărată doar dacă a>b.
Dacă a>b și xa=yb, se arată și că (x+a)>(y+b),
prin același raționament prin care s-a arătat că (y+b)>(x+a).
Și se ajunge la contradicția :
(y+b)>(x+a) și (x+a)>(y+b).
Pentru că știm sigur că y>x, din contradicția de mai sus rezultă că a nu este mai mare ca b, pentru că altfel se ajunge la contradicția respectivă.
Dacă a nu este mai mare ca b, iar y>x, rezultă că yb>xa.
De aici rezultă că egalitatea xa=yb este adevărată doar dacă a=b=0,
de unde rezultă că n nu poate fi diferit de 2,
așa cum am arătat în mesajul anterior.
Mai simplu, nu ?
Deci,
Notăm pentru simpificare
Am arătat în mesajul anterior că dacă y>x și xa=yb, atunci (y+b)>(x+a).
Dar dacă y>x, egalitatea xa=yb este adevărată doar dacă a>b.
Dacă a>b și xa=yb, se arată și că (x+a)>(y+b),
prin același raționament prin care s-a arătat că (y+b)>(x+a).
Și se ajunge la contradicția :
(y+b)>(x+a) și (x+a)>(y+b).
Pentru că știm sigur că y>x, din contradicția de mai sus rezultă că a nu este mai mare ca b, pentru că altfel se ajunge la contradicția respectivă.
Dacă a nu este mai mare ca b, iar y>x, rezultă că yb>xa.
De aici rezultă că egalitatea xa=yb este adevărată doar dacă a=b=0,
de unde rezultă că n nu poate fi diferit de 2,
așa cum am arătat în mesajul anterior.
Mai simplu, nu ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Stați puțin...
ceva nu este în regulă !
Incoerențele de mai sus au legătură și cu conjectura abc !
Pentru că raportăm produsul unor numere la suma lor.
Ia să mai analizăm !
ceva nu este în regulă !
Incoerențele de mai sus au legătură și cu conjectura abc !
Pentru că raportăm produsul unor numere la suma lor.
Ia să mai analizăm !
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Nu sunt suficiente condițiile y>x și ax=yb, pentru a rezulta că :

Condițiile complete sunt :
ax=yb și
y>x>a>b.
Știm că y>x, iar egalitatea
![\dpi{150} \mathbf{ x\cdot \left [ cosB-\frac{x^{n-1}}{z^{n-1}} \right ]=y\cdot\left [ \frac{y^{n-1}}{z^{n-1}}- cosC\right ] }](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{ x\cdot \left [ cosB-\frac{x^{n-1}}{z^{n-1}} \right ]=y\cdot\left [ \frac{y^{n-1}}{z^{n-1}}- cosC\right ] }) .
.
este adevărată doar dacă a>b, atât timp cât y>x, unde
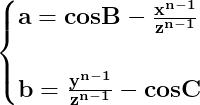
Pentru că x>a, în prima egalitate de mai sus este îndeplinită și condiția y>x>a>b
Luăm un exemplu simplu :
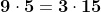
Dacă x este 3 și y este 5 sau 9, nu are loc inegalitatea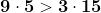 .
.
Dacă x este 5 și y 15 are loc inegalitatea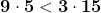 , dar nu se respectă condiția ca 5 >9.
, dar nu se respectă condiția ca 5 >9.
Se pare că aceste cazuri trebuiesc analizate ceva mai profund,
iar pentru a valida demonstrația de mai sus trebuie și o demonstrație pentru faptul că sunt suficiente condițiile
ax=yb și
y>x>a>b
pentru a rezulta sistemul
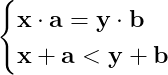
Oricum, aceste exprimări ale unei egalități prin raportarea produsului la sumă pot fi folositoare pentru a ajunge la anumite concluzii în ceea ce privește conjectura abc.
Cred că o voi analiza ceva mai profund după ce mă asigur că demonstrația elementară a teoremei lui Fermat este corectă și completă.
Condițiile complete sunt :
ax=yb și
y>x>a>b.
Știm că y>x, iar egalitatea
este adevărată doar dacă a>b, atât timp cât y>x, unde
Pentru că x>a, în prima egalitate de mai sus este îndeplinită și condiția y>x>a>b
Luăm un exemplu simplu :
Dacă x este 3 și y este 5 sau 9, nu are loc inegalitatea
Dacă x este 5 și y 15 are loc inegalitatea
Se pare că aceste cazuri trebuiesc analizate ceva mai profund,
iar pentru a valida demonstrația de mai sus trebuie și o demonstrație pentru faptul că sunt suficiente condițiile
ax=yb și
y>x>a>b
pentru a rezulta sistemul
Oricum, aceste exprimări ale unei egalități prin raportarea produsului la sumă pot fi folositoare pentru a ajunge la anumite concluzii în ceea ce privește conjectura abc.
Cred că o voi analiza ceva mai profund după ce mă asigur că demonstrația elementară a teoremei lui Fermat este corectă și completă.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
curiosul a scris:
Luăm un exemplu simplu :
Dacă x este 3 și y este 5 sau 9, nu are loc inegalitatea.
Dacă x este 5 și y 15 are loc inegalitatea, dar nu se respectă condiția ca 5 >9.
Am vrut să spun, dar nu am mai avut timp să editez (și aș ruga administratorul dacă poate mări cu vreo 5 minute timpul de editare) :
Luăm un exemplu simplu :
Dacă x este 3 și y este 5 sau 9, nu are loc inegalitatea
Dacă x este 5 și y 15 are loc inegalitatea
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
Pagina 1 din 2 • 1, 2 
 Subiecte similare
Subiecte similare» Greşeli în subiectul : Demonstraţia elementară a Teoremei lui Fermat
» Demonstrațiile cazurilor particulare ale Marii teoreme a lui Fermat
» O demonstrație elementară pentru Marea teoremă a lui Fermat
» Demonstrațiile cazurilor particulare ale Marii teoreme a lui Fermat
» O demonstrație elementară pentru Marea teoremă a lui Fermat
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 1 din 2
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 