Ultimele subiecte
» Grup de cercetare pentru constiintaScris de CAdi Astazi la 05:08
» OZN in Romania
Scris de CAdi Ieri la 20:05
» Fotografia astronomica.
Scris de virgil Ieri la 19:32
» Structura atomului
Scris de virgil Lun 02 Sept 2024, 20:16
» Ce fel de popor suntem
Scris de eugen Lun 02 Sept 2024, 14:54
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Lun 02 Sept 2024, 07:45
» Unde a ajuns stiinta ?
Scris de virgil Mar 27 Aug 2024, 17:55
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de CAdi Lun 26 Aug 2024, 15:08
» URME ALE EXTRATERESTRILOR PE PAMANT. DESCOPERIRI INEXPLICABILE SI FENOMENE OZN 1
Scris de CAdi Dum 25 Aug 2024, 23:21
» PROFILUL CERCETATORULUI...
Scris de eugen Dum 25 Aug 2024, 11:27
» Experimentul Pound Rebka
Scris de virgil Lun 19 Aug 2024, 18:14
» Microundele
Scris de CAdi Vin 16 Aug 2024, 11:11
» Transilvania-pamant stramosesc
Scris de CAdi Mier 14 Aug 2024, 06:55
» Basarabia, Bucovina - pământ românesc
Scris de CAdi Mar 13 Aug 2024, 11:54
» Scrierea dacilor
Scris de CAdi Lun 12 Aug 2024, 19:58
» Sanatate- Diverse
Scris de eugen Sam 10 Aug 2024, 10:01
» Daci nemuritori
Scris de eugen Vin 09 Aug 2024, 22:10
» Suntem indexaţi de motoarele de căutare?
Scris de CAdi Mar 06 Aug 2024, 15:58
» Impulsul elicoidal
Scris de virgil Joi 01 Aug 2024, 21:01
» Constatari
Scris de CAdi Joi 01 Aug 2024, 06:36
» New topic
Scris de ilasus Mier 31 Iul 2024, 20:54
» Globalizarea
Scris de eugen Sam 27 Iul 2024, 12:44
» Fenomene Electromagnetice
Scris de eugen Lun 22 Iul 2024, 21:37
» Sa mai auzim si de bine in Romania :
Scris de virgil Lun 22 Iul 2024, 18:39
» Masina Timpului
Scris de CAdi Lun 22 Iul 2024, 13:17
» Ce este FOIP?
Scris de Abel Cavaşi Vin 19 Iul 2024, 22:02
» Inertia
Scris de virgil Mier 17 Iul 2024, 11:09
» Lucrul mecanic - definitie si exemple (Secţiunea 2)
Scris de CAdi Mar 16 Iul 2024, 05:20
» Laborator-sa construim impreuna
Scris de eugen Lun 15 Iul 2024, 10:17
» Stanley A. Meyer - Hidrogen
Scris de eugen Dum 14 Iul 2024, 20:25
Postări cu cele mai multe reacții ale lunii
» Mesaj de la Razvan în Fotografia astronomica. ( 3 )
» Mesaj de la eugen în Ce fel de popor suntem
( 2 )
» Mesaj de la Razvan în Fotografia astronomica.
( 2 )
» Mesaj de la Abel Cavaşi în TEORIA CONSPIRATIEI NU ESTE UN MIT...
( 1 )
» Mesaj de la eugen în Fotografia astronomica.
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12369) | ||||
| CAdi (12260) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7952) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6170) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3910) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Spune şi altora
Cine este conectat?
În total sunt 34 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 34 Vizitatori :: 2 Motoare de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
5 participanți
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 2 din 2
Pagina 2 din 2 •  1, 2
1, 2
 Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Rezumarea primului mesaj :
Ce nu-ți convine la demonstrația asta Dacule ?
Faptul că este plecată de la sistemul tău ?
Faptul că ai falsa părere că meritele tale nu ar mai fi la fel de mari ?
Greșești.
Acesta este un cont nou.
Vedeți voi (administratorii) care le eliminați.
Dacă vreți, puteți să le eliminați pe amândouă,
n-am nimic împotrivă.
În orice triunghi este adevărată relația :
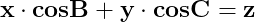
și de asemenea
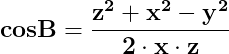
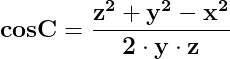
unde x, y, z sunt laturile triunghiului, iar cosB și cosC,
cosinusurile unghiurilor formate de laturile x și z, respectiv y și z.
Deci în orice triunghi este valabilă egalitatea (1):
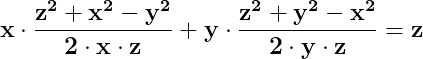
Dacă între laturile x, y, z ale unui triunghi este adevărată și egalitatea :
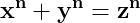
rezultă că este adevărată și egalitatea (2):
![\dpi{150} \mathbf{\frac{z^n}{z^{n-1}}=\frac{x^n+y^n}{z^{n-1}}=\frac{x^n}{z^{n-1}}+\frac{y^n}{z^{n-1}}=\left [ x\cdot \frac{x^{n-1}}{z^{n-1}}+y\cdot \frac{y^{n-1}}{z^{n-1}}=z \right ]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{\frac{z^n}{z^{n-1}}=\frac{x^n+y^n}{z^{n-1}}=\frac{x^n}{z^{n-1}}+\frac{y^n}{z^{n-1}}=\left [ x\cdot \frac{x^{n-1}}{z^{n-1}}+y\cdot \frac{y^{n-1}}{z^{n-1}}=z \right ]})
Pentru că
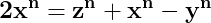
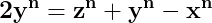
atunci putem scrie
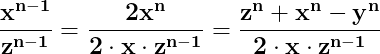
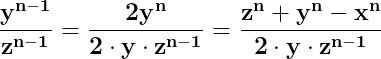
Înlocuind în egalitatea (2), ajungem să stabilim că dacă între laturile x, y, z ale unui triunghi este adevărată
egalitatea ,
,
atunci în acel tiunghi este adevărată egalitatea (3):
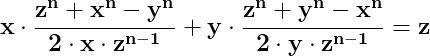
În concluzie, în triunghiul în care are loc și egalitatea , atunci în acel triunghi sunt simultan adevărate egalitățile (1)și
, atunci în acel triunghi sunt simultan adevărate egalitățile (1)și
(3):
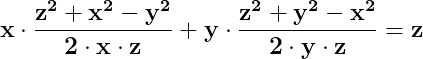
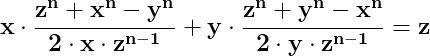
De unde rezultă că :
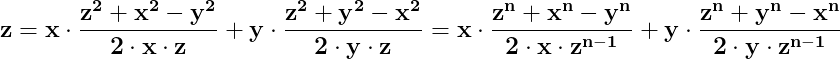
Pentru că din egalitatea de mai sus, în orice triunghi este adevărată relația
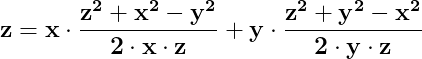
rezultă evident că pentru n diferit de 2, în același triunghi nu poate fi adevărată egalitatea :
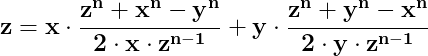
Deși x, y, z nu pot fi laturile unui triunghi dacă x+y=z,
pentru n=1, ecuația are soluții reale.
are soluții reale.
Pentru că laturile x, y, z ale triunghiului pot fi oricare numere reale,
ce îndeplinesc condițiile x+y>z , y+z>x , x+z>y,
ecuația nu are soluții
nu are soluții
reale pentru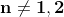 .
.
Q.E.D
Ce nu-ți convine la demonstrația asta Dacule ?
Faptul că este plecată de la sistemul tău ?
Faptul că ai falsa părere că meritele tale nu ar mai fi la fel de mari ?
Greșești.
Acesta este un cont nou.
Vedeți voi (administratorii) care le eliminați.
Dacă vreți, puteți să le eliminați pe amândouă,
n-am nimic împotrivă.
În orice triunghi este adevărată relația :
și de asemenea
unde x, y, z sunt laturile triunghiului, iar cosB și cosC,
cosinusurile unghiurilor formate de laturile x și z, respectiv y și z.
Deci în orice triunghi este valabilă egalitatea (1):
Dacă între laturile x, y, z ale unui triunghi este adevărată și egalitatea :
rezultă că este adevărată și egalitatea (2):
Pentru că
atunci putem scrie
Înlocuind în egalitatea (2), ajungem să stabilim că dacă între laturile x, y, z ale unui triunghi este adevărată
egalitatea
atunci în acel tiunghi este adevărată egalitatea (3):
În concluzie, în triunghiul în care are loc și egalitatea
(3):
De unde rezultă că :
Pentru că din egalitatea de mai sus, în orice triunghi este adevărată relația
rezultă evident că pentru n diferit de 2, în același triunghi nu poate fi adevărată egalitatea :
Deși x, y, z nu pot fi laturile unui triunghi dacă x+y=z,
pentru n=1, ecuația
Pentru că laturile x, y, z ale triunghiului pot fi oricare numere reale,
ce îndeplinesc condițiile x+y>z , y+z>x , x+z>y,
ecuația
reale pentru
Q.E.D
Curi_osul- Mulţumit de forum : Numarul mesajelor : 7




Puncte : 12594
Data de inscriere : 22/03/2013
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Nu sunt suficiente condițiile y>x și ax=yb, pentru a rezulta că :

Condițiile complete sunt :
ax=yb și
y>x>a>b.
Știm că y>x, iar egalitatea
![\dpi{150} \mathbf{ x\cdot \left [ cosB-\frac{x^{n-1}}{z^{n-1}} \right ]=y\cdot\left [ \frac{y^{n-1}}{z^{n-1}}- cosC\right ] }](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{ x\cdot \left [ cosB-\frac{x^{n-1}}{z^{n-1}} \right ]=y\cdot\left [ \frac{y^{n-1}}{z^{n-1}}- cosC\right ] }) .
.
este adevărată doar dacă a>b, atât timp cât y>x, unde
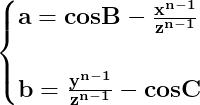
Pentru că x>a, în prima egalitate de mai sus este îndeplinită și condiția y>x>a>b
Luăm un exemplu simplu :
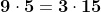
Dacă x este 3 și y este 5 sau 9, nu are loc inegalitatea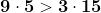 .
.
Dacă x este 5 și y 15 are loc inegalitatea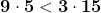 , dar nu se respectă condiția ca 5 >9.
, dar nu se respectă condiția ca 5 >9.
Se pare că aceste cazuri trebuiesc analizate ceva mai profund,
iar pentru a valida demonstrația de mai sus trebuie și o demonstrație pentru faptul că sunt suficiente condițiile
ax=yb și
y>x>a>b
pentru a rezulta sistemul
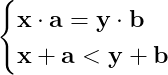
Oricum, aceste exprimări ale unei egalități prin raportarea produsului la sumă pot fi folositoare pentru a ajunge la anumite concluzii în ceea ce privește conjectura abc.
Cred că o voi analiza ceva mai profund după ce mă asigur că demonstrația elementară a teoremei lui Fermat este corectă și completă.
Condițiile complete sunt :
ax=yb și
y>x>a>b.
Știm că y>x, iar egalitatea
este adevărată doar dacă a>b, atât timp cât y>x, unde
Pentru că x>a, în prima egalitate de mai sus este îndeplinită și condiția y>x>a>b
Luăm un exemplu simplu :
Dacă x este 3 și y este 5 sau 9, nu are loc inegalitatea
Dacă x este 5 și y 15 are loc inegalitatea
Se pare că aceste cazuri trebuiesc analizate ceva mai profund,
iar pentru a valida demonstrația de mai sus trebuie și o demonstrație pentru faptul că sunt suficiente condițiile
ax=yb și
y>x>a>b
pentru a rezulta sistemul
Oricum, aceste exprimări ale unei egalități prin raportarea produsului la sumă pot fi folositoare pentru a ajunge la anumite concluzii în ceea ce privește conjectura abc.
Cred că o voi analiza ceva mai profund după ce mă asigur că demonstrația elementară a teoremei lui Fermat este corectă și completă.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Numarul mesajelor : 6790
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
curiosul a scris:
Luăm un exemplu simplu :
Dacă x este 3 și y este 5 sau 9, nu are loc inegalitatea.
Dacă x este 5 și y 15 are loc inegalitatea, dar nu se respectă condiția ca 5 >9.
Am vrut să spun, dar nu am mai avut timp să editez (și aș ruga administratorul dacă poate mări cu vreo 5 minute timpul de editare) :
Luăm un exemplu simplu :
Dacă x este 3 și y este 5 sau 9, nu are loc inegalitatea
Dacă x este 5 și y 15 are loc inegalitatea
curiosul- Banat temporar pentru comportamentul nepotrivit
- Numarul mesajelor : 6790
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Nici aceasta nu este o demonstrație corectă,
pentru că ar însemna că pentru orice x,a,y, b,
dacă y>x, a=b=0, iar acest lucru nu este generalizat pentru orice x, a, y, b.
Deci să vedem cum corectăm greșeala.
pentru că ar însemna că pentru orice x,a,y, b,
dacă y>x, a=b=0, iar acest lucru nu este generalizat pentru orice x, a, y, b.
Deci să vedem cum corectăm greșeala.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41326
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Iar greșeala din demonstrație este cea de mai jos :
Să presupunem că dacă y > x și ax = yb rezultă că y+b > x+a.
După care am separat termenii y și a de o parte și de alta a egalității și am înmulțit cu ab :
b-a > x-y
ab(b-a) > ab(x-y)
Firește, aceasta doar dacă considerăm ab diferit de 0.
Cazul A .
ab > 0
Pentru că y > x , termenul din dreapta este negativ.
Inegalitatea este corectă dacă :
1. b-a > 0
2. 0 > b-a și x-y > b-a
În cazul 2 sunt necesare ambele condiții pentru că valoarea negativă a lui b-a trebuie să fie mai mică în modul ca cea a valorii negative x-y în modul, pentru ca ab(b-a) > ab(x-y).
Dar inegalitatea x-y > b-a contrazice inegalitatea inițială y+b > x+a.
În cazul 1. dacă b-a > 0, atunci pentru că y > x, nu există egalitatea ax = yb.
Cazul B
0 > ab
În această situație situația este inversă celei din cazul A și se ajunge la aceleași concluzii.
Prin urmare trebuiesc analizate doar cazurile care nu contrazic
egalitatea inițială xa = yb și inegalitatea y+b > x+a.
Se pare că în orice demonstrație corectă la prima vedere, pot fi strecurate greșeli aproape insesizabile.
Să presupunem că dacă y > x și ax = yb rezultă că y+b > x+a.
După care am separat termenii y și a de o parte și de alta a egalității și am înmulțit cu ab :
b-a > x-y
ab(b-a) > ab(x-y)
Firește, aceasta doar dacă considerăm ab diferit de 0.
Cazul A .
ab > 0
Pentru că y > x , termenul din dreapta este negativ.
Inegalitatea este corectă dacă :
1. b-a > 0
2. 0 > b-a și x-y > b-a
În cazul 2 sunt necesare ambele condiții pentru că valoarea negativă a lui b-a trebuie să fie mai mică în modul ca cea a valorii negative x-y în modul, pentru ca ab(b-a) > ab(x-y).
Dar inegalitatea x-y > b-a contrazice inegalitatea inițială y+b > x+a.
În cazul 1. dacă b-a > 0, atunci pentru că y > x, nu există egalitatea ax = yb.
Cazul B
0 > ab
În această situație situația este inversă celei din cazul A și se ajunge la aceleași concluzii.
Prin urmare trebuiesc analizate doar cazurile care nu contrazic
egalitatea inițială xa = yb și inegalitatea y+b > x+a.
Se pare că în orice demonstrație corectă la prima vedere, pot fi strecurate greșeli aproape insesizabile.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41326
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Uraaaaa !!!
Gata, am găsit !
Acum se poate demonstra corect și făra greșeală că a=b=0,
pe baza raționamentului de mai sus.
Gata, am găsit !
Acum se poate demonstra corect și făra greșeală că a=b=0,
pe baza raționamentului de mai sus.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41326
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Să mai analizăm o dată demonstrația.
Pentru ceea ce am scris mai jos mai trebuie adăugat ceva.
Corect, dar și cu condiția ca x>b.
Pentru ceea ce am scris mai jos mai trebuie adăugat ceva.
curiosul a scris:
Deci dacă într-un triunghi sunt adevărate relațiile din primul sistem de mai jos, sunt adevărate și relațiile din al doilea sistem de mai jos :
Corect, dar și cu condiția ca x>b.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41326
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Și într-adevăr, există o altă variantă cu un raționament mai eficient și mult mai ușor de verificat.
O mai analizez un pic să fiu sigur și o să o scriu mai târziu.
O mai analizez un pic să fiu sigur și o să o scriu mai târziu.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41326
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Iar greșeala din ultima demonstrație este aici:
Pentru că dacă xa=yb și y>x, atunci a trebuie să fie mai mare ca b (a>b).
În citatul de mai sus, am simplificat cu (b-a), adică cu un număr negativ, iar asta schimbă sensul inegalității.
Aici este greșeala !
Să văd dacă noul raționament are și acest tip de greșeli mai greu de sesizat la prima vedere.
curiosul a scris:
Pentru că dacă xa=yb și y>x, atunci a trebuie să fie mai mare ca b (a>b).
În citatul de mai sus, am simplificat cu (b-a), adică cu un număr negativ, iar asta schimbă sensul inegalității.
Aici este greșeala !
Să văd dacă noul raționament are și acest tip de greșeli mai greu de sesizat la prima vedere.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41326
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Gata, am găsit.
Dar scriu numai concluziile acum și voi scrie demonstrația completă mai târziu sau mâine dimineață.
Vă las până atunci să trageți concluziile :
Deci soluțiile x, y, z ale ecuației pot fi considerate laturile unui triunghi.
pot fi considerate laturile unui triunghi.
Presupunem adevărată egalitatea între laturile unui triunghi și putem așadar, construi sistemul :
între laturile unui triunghi și putem așadar, construi sistemul :
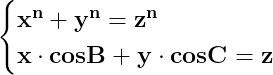
unde unghiurile B și C sunt unghiurile formate de laturile x și z, respectiv y și z.
Înmulțim cu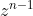 termenii celei de-a doua egalități a sistemului și ajungem la :
termenii celei de-a doua egalități a sistemului și ajungem la :
![\dpi{150} \mathbf{z^{n-1}\left [ x\cdot cosB+y\cdot cosC \right ]=z^n=x^n+y^n}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{z^{n-1}\left [ x\cdot cosB+y\cdot cosC \right ]=z^n=x^n+y^n})
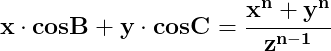
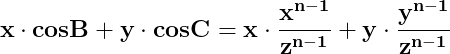
Soluțiile acestei ecuații sunt :
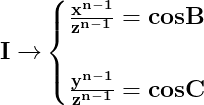
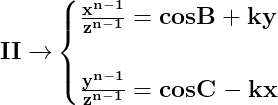
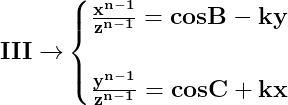
Ecuația nu poate avea alte soluții.
Demonstrația corectă și completă o s-o scriu mai târziu.
În sfârșit !!!
Dar scriu numai concluziile acum și voi scrie demonstrația completă mai târziu sau mâine dimineață.
Vă las până atunci să trageți concluziile :
Deci soluțiile x, y, z ale ecuației
Presupunem adevărată egalitatea
unde unghiurile B și C sunt unghiurile formate de laturile x și z, respectiv y și z.
Înmulțim cu
Soluțiile acestei ecuații sunt :
Ecuația nu poate avea alte soluții.
Demonstrația corectă și completă o s-o scriu mai târziu.
În sfârșit !!!
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41326
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Sa-mi lasi si mie un pm cand te hotarasti in sfarsit care e demonstratia finala.

Forever_Man- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 982




Puncte : 15909
Data de inscriere : 25/11/2012
Obiective curente : https://philpeople.org/profiles/cosmin-visan -

 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
"Pentru n>2, ecuația  nu are soluții întregi."
nu are soluții întregi."
Stabilim în primul rând că valorile x, y, z trebuie să fie laturile unui triunghi.
Dacă ecuația are soluții, atunci (x+y)>z>y.
are soluții, atunci (x+y)>z>y.
Condiția (x+y)>z>y este îndeplinită de laturile x, y, z ale unui triunghi, cu z>y>x.
Deci soluțiile x, y, z ale ecuației pot fi considerate laturile unui triunghi.
pot fi considerate laturile unui triunghi.
Presupunem adevărată egalitatea între laturile unui triunghi și putem așadar, construi sistemul :
între laturile unui triunghi și putem așadar, construi sistemul :
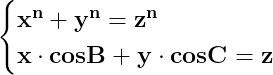
unde unghiurile B și C sunt unghiurile formate de laturile x și z, respectiv y și z.
Înmulțim cu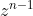 termenii celei de-a doua egalități a sistemului și ajungem la :
termenii celei de-a doua egalități a sistemului și ajungem la :
![\dpi{150} \mathbf{z^{n-1}\left [ x\cdot cosB+y\cdot cosC \right ]=z^n=x^n+y^n}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{z^{n-1}\left [ x\cdot cosB+y\cdot cosC \right ]=z^n=x^n+y^n})
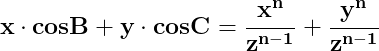
![\dpi{150} \mathbf{ x\cdot\left [ cosB- \frac{x^{n-1}}{z^{n-1}}\right ]= y\cdot\left [ \frac{y^{n-1}}{z^{n-1}}- cosC \right ]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{ x\cdot\left [ cosB- \frac{x^{n-1}}{z^{n-1}}\right ]= y\cdot\left [ \frac{y^{n-1}}{z^{n-1}}- cosC \right ]})
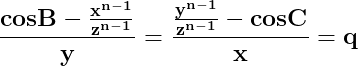
De aici putem forma sistemul :

![\dpi{150} \Leftrightarrow \begin{cases} \mathbf{x\cdot \left [ \frac{ cosB- \frac{x^{n-1}}{z^{n-1}}}{q} \right ]=x\cdot y} \\ \\ \mathbf{y\cdot \left [ \frac{\frac{y^{n-1}}{z^{n-1}}- cosC }{q} \right ] =x\cdot y \end{cases}}\Leftrightarrow \begin{cases} \mathbf{\frac{ x\cdot cosB- x\cdot \frac{x^{n-1}}{z^{n-1}}}{q} =x\cdot y} \\ \\ \mathbf{\frac{y\cdot \frac{y^{n-1}}{z^{n-1}}- y\cdot cosC }{q} =x\cdot y \end{cases}}](http://latex.codecogs.com/gif.latex?\dpi{150} \Leftrightarrow \begin{cases} \mathbf{x\cdot \left [ \frac{ cosB- \frac{x^{n-1}}{z^{n-1}}}{q} \right ]=x\cdot y} \\ \\ \mathbf{y\cdot \left [ \frac{\frac{y^{n-1}}{z^{n-1}}- cosC }{q} \right ] =x\cdot y \end{cases}}\Leftrightarrow \begin{cases} \mathbf{\frac{ x\cdot cosB- x\cdot \frac{x^{n-1}}{z^{n-1}}}{q} =x\cdot y} \\ \\ \mathbf{\frac{y\cdot \frac{y^{n-1}}{z^{n-1}}- y\cdot cosC }{q} =x\cdot y \end{cases}})
Din cele două egalități ale sistemului rezultă egalitatea :
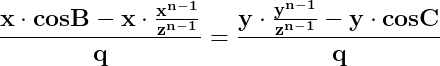
Dar din sistemul inițial rezultă că
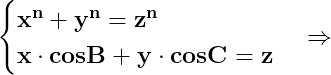
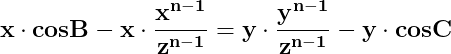
și s-a ajuns la relațiile sistemului :
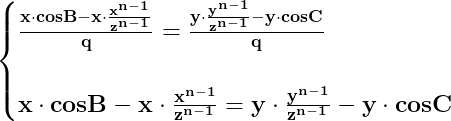
De aici rezultă evident că q este egal cu 1.
Revenind la sistemul soluțiilor ecuației pentru q=1 :

Dacă x , y sunt reale mai mari sau egale cu 1, ar însemna că în dreapta egalităților fie unul din cei doi termeni este negativ, deci și cosinusul respectiv, ceea ce este incorect, fie într-una din relații un termen este supraunitar, iar celălalt subunitar, de unde rezultă că sistemul, și implicit ecuația inițială, admite soluții doar pentru q=0 :


Egalitățile de mai sus sunt adevărate doar pentru n=2.
Dacă laturile x, y, z ale triunghiului sunt considerate oricare numere reale mai mari/egale cu 1
care îndeplinesc condițiile x+y>z , x+z>y și y+z>x,
putem afirma că pentru n diferit de 2,
între laturile unui triunghi nu poate fi adevărată egalitatea
și generalizat ecuația respectivă nu are soluții reale x, y, z, n pentru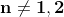 ,
,
deoarece ecuația are soluții reale și pentru n=1, deși x+y=z, nu pot fi laturile unui triunghi .
Observație
Analiza de mai sus este bazată pe observația utilizatorului Dacu, care a stabilit relația dintre laturile triunghiului și soluțiile ecuației din Marea teoremă a lui Fermat.
Stabilim în primul rând că valorile x, y, z trebuie să fie laturile unui triunghi.
Dacă ecuația
Condiția (x+y)>z>y este îndeplinită de laturile x, y, z ale unui triunghi, cu z>y>x.
Deci soluțiile x, y, z ale ecuației
Presupunem adevărată egalitatea
unde unghiurile B și C sunt unghiurile formate de laturile x și z, respectiv y și z.
Înmulțim cu
De aici putem forma sistemul :
Din cele două egalități ale sistemului rezultă egalitatea :
Dar din sistemul inițial rezultă că
și s-a ajuns la relațiile sistemului :
De aici rezultă evident că q este egal cu 1.
Revenind la sistemul soluțiilor ecuației pentru q=1 :
Dacă x , y sunt reale mai mari sau egale cu 1, ar însemna că în dreapta egalităților fie unul din cei doi termeni este negativ, deci și cosinusul respectiv, ceea ce este incorect, fie într-una din relații un termen este supraunitar, iar celălalt subunitar, de unde rezultă că sistemul, și implicit ecuația inițială, admite soluții doar pentru q=0 :
Egalitățile de mai sus sunt adevărate doar pentru n=2.
Dacă laturile x, y, z ale triunghiului sunt considerate oricare numere reale mai mari/egale cu 1
care îndeplinesc condițiile x+y>z , x+z>y și y+z>x,
putem afirma că pentru n diferit de 2,
între laturile unui triunghi nu poate fi adevărată egalitatea
și generalizat ecuația respectivă nu are soluții reale x, y, z, n pentru
deoarece ecuația are soluții reale și pentru n=1, deși x+y=z, nu pot fi laturile unui triunghi .
Observație
Analiza de mai sus este bazată pe observația utilizatorului Dacu, care a stabilit relația dintre laturile triunghiului și soluțiile ecuației din Marea teoremă a lui Fermat.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41326
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Nu e corectă nici asta :
Prima este adevărată dacă a doua este adevărată.
curiosul a scris:
De aici rezultă evident că q este egal cu 1.
Prima este adevărată dacă a doua este adevărată.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41326
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Problema analizată prin prisma laturilor unui triunghi se reduce într-un fel sau altul, la a arăta că nu există niciun număr, chiar și real, astfel încât, adunat sau scăzut la un număr de forma :
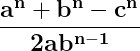
să se obțină tot un număr de aceeași formă, dar la o putere diferită:
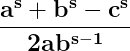
Dacă se arată că nu poate exista un asemenea număr este suficient să demonstreze teorema prin relaționarea soluțiilor ecuației la laturile unui triunghi.
Prin metode elementare de bază nu se poate.
Sau cel puțin eu nu am reușit până acum.
Dar probabil că o să mai încerc.
să se obțină tot un număr de aceeași formă, dar la o putere diferită:
Dacă se arată că nu poate exista un asemenea număr este suficient să demonstreze teorema prin relaționarea soluțiilor ecuației la laturile unui triunghi.
Prin metode elementare de bază nu se poate.
Sau cel puțin eu nu am reușit până acum.
Dar probabil că o să mai încerc.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41326
Data de inscriere : 22/03/2011
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41326
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Citez :
" N-a fost un eșec, am reușit să dezvolt o multitudine de demonstrații greșite."
" N-a fost un eșec, am reușit să dezvolt o multitudine de demonstrații greșite."
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41326
Data de inscriere : 22/03/2011
 Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Re: Cea mai simplă demonstrație elementară a Marii Teoreme a lui Fermat
Mai am o variantă, "corectă", firește.
Dar acum am pățit ca în bancul cu lupul.
Vrea cineva să o scriu ?
Dacă v-ați săturat de atâtea demonstrații "corecte", vă înțeleg.
Dar dacă cineva mai este interesat de o altă versiune, o voi scrie și pe asta.
Are un cu totul alt raționament.
Dar acum am pățit ca în bancul cu lupul.
Vrea cineva să o scriu ?
Dacă v-ați săturat de atâtea demonstrații "corecte", vă înțeleg.
Dar dacă cineva mai este interesat de o altă versiune, o voi scrie și pe asta.
Are un cu totul alt raționament.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41326
Data de inscriere : 22/03/2011
Pagina 2 din 2 •  1, 2
1, 2
 Subiecte similare
Subiecte similare» Greşeli în subiectul : Demonstraţia elementară a Teoremei lui Fermat
» Demonstrațiile cazurilor particulare ale Marii teoreme a lui Fermat
» O demonstrație elementară pentru Marea teoremă a lui Fermat
» Demonstrațiile cazurilor particulare ale Marii teoreme a lui Fermat
» O demonstrație elementară pentru Marea teoremă a lui Fermat
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 2 din 2
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum|
|
|




 Devino fan Forumgratuit
Devino fan Forumgratuit 
