Ultimele subiecte
» Impulsul elicoidalScris de virgil Joi 25 Iul 2024, 17:43
» New topic
Scris de virgil Mier 24 Iul 2024, 07:33
» Ce fel de popor suntem
Scris de CAdi Mar 23 Iul 2024, 22:12
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de CAdi Mar 23 Iul 2024, 06:47
» Fenomene Electromagnetice
Scris de eugen Lun 22 Iul 2024, 21:37
» Sa mai auzim si de bine in Romania :
Scris de virgil Lun 22 Iul 2024, 18:39
» Masina Timpului
Scris de CAdi Lun 22 Iul 2024, 13:17
» Globalizarea
Scris de virgil Dum 21 Iul 2024, 16:46
» Unde a ajuns stiinta ?
Scris de CAdi Dum 21 Iul 2024, 15:20
» Ce este FOIP?
Scris de Abel Cavaşi Vin 19 Iul 2024, 22:02
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de CAdi Joi 18 Iul 2024, 11:51
» Inertia
Scris de virgil Mier 17 Iul 2024, 11:09
» Lucrul mecanic - definitie si exemple (Secţiunea 2)
Scris de CAdi Mar 16 Iul 2024, 05:20
» Laborator-sa construim impreuna
Scris de eugen Lun 15 Iul 2024, 10:17
» Stanley A. Meyer - Hidrogen
Scris de eugen Dum 14 Iul 2024, 20:25
» Despre vise
Scris de CAdi Sam 13 Iul 2024, 15:09
» Constatari
Scris de curiosul Sam 13 Iul 2024, 10:13
» Pendulul
Scris de virgil_48 Lun 08 Iul 2024, 16:18
» Marea teorema a lui Fermat.
Scris de curiosul Sam 06 Iul 2024, 10:23
» Legi de conservare (2)
Scris de Vizitator Vin 05 Iul 2024, 13:24
» PROFILUL CERCETATORULUI...
Scris de virgil Dum 30 Iun 2024, 19:01
» Grup de cercetare pentru constiinta
Scris de curiosul Sam 29 Iun 2024, 16:06
» CURIOZITATI; Motor miniatural functional
Scris de virgil Vin 28 Iun 2024, 20:36
» Fizicieni care au schimbat lumea.
Scris de eugen Vin 28 Iun 2024, 09:58
» O proprietate Black Hole (Gaura Neagra)
Scris de virgil Joi 27 Iun 2024, 17:58
» Cum marim energia atomului ?
Scris de virgil Dum 23 Iun 2024, 19:11
» Bec Tapo L530E 2.0 - Smart Wi-Fi Light Bulb, Multicolor
Scris de Dacu Vin 21 Iun 2024, 18:30
» Caracteristicile tehnice ale motoarelor auto
Scris de CAdi Joi 20 Iun 2024, 12:24
» Concluzii asupra relativității
Scris de curiosul Dum 16 Iun 2024, 11:55
» EMINESCU, Templu National
Scris de eugen Sam 15 Iun 2024, 22:29
Postări cu cele mai multe reacții ale lunii
» Mesaj de la CAdi în TEORIA CONSPIRATIEI NU ESTE UN MIT... ( 2 )
» Mesaj de la eugen în Laborator-sa construim impreuna
( 2 )
» Mesaj de la eugen în Laborator-sa construim impreuna
( 2 )
» Mesaj de la virgil în Sa mai auzim si de bine in Romania :
( 2 )
» Mesaj de la CAdi în TEORIA CONSPIRATIEI NU ESTE UN MIT...
( 2 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12347) | ||||
| CAdi (12205) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7950) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6162) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3889) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Spune şi altora
Cine este conectat?
În total sunt 38 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 38 Vizitatori :: 2 Motoare de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Marea teorema a lui Fermat.
+7
fanel
Syntax
Abel Cavaşi
Dacu
CAdi
curiosul
meteor
11 participanți
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 12 din 13
Pagina 12 din 13 •  1, 2, 3 ... , 11, 12, 13
1, 2, 3 ... , 11, 12, 13 
 Marea teorema a lui Fermat.
Marea teorema a lui Fermat.
Ultima editare efectuata de catre meteor in Vin 15 Mar 2013, 22:53, editata de 1 ori
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25489
Data de inscriere : 19/06/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
N-ai zis rău ce ai zis, dar nu trebuie neapărat rezolvat vreun sistem de ecuații.
S-ar putea să fie nevoie de implicarea exprimării unui cosinus, dar ideea în sine este că dacă x, y, z sunt întregi, iar p^2 rațional, în exprimarea lui p^2 sub formă de fracție ireductibila a/b , a, b, ar trebui să fie pătrate perfecte.
Trebuie arătat că rădăcina pătrată a lui p este un număr rațional, nu irațional.
Revin.
S-ar putea să fie nevoie de implicarea exprimării unui cosinus, dar ideea în sine este că dacă x, y, z sunt întregi, iar p^2 rațional, în exprimarea lui p^2 sub formă de fracție ireductibila a/b , a, b, ar trebui să fie pătrate perfecte.
Trebuie arătat că rădăcina pătrată a lui p este un număr rațional, nu irațional.
Revin.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Numarul mesajelor : 6790
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Dacă îmi demonstrezi asta, eu demonstrez restul.Dacu a scris:Cert este că dacă x mai mic ca y mai mic ca z sunt numere naturale nenule atunci în mod sigur AD este un număr rațional mai mare ca zero.
Dar AD, nu AD^2.
Dacă x, y, z sunt întregi.
Dacă AD este rațional, sub formă de fracție ireductibila a/b, atunci AD^2 trebuie obligatoriu să fie cu numărătorul și numitorul pătrate perfecte.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Numarul mesajelor : 6790
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Deoarece tu ai considerat altă relație de ordine între laturile trunghiului și o altă poziție a punctuluicuriosul a scris:Dacă îmi demonstrezi asta, eu demonstrez restul.Dacu a scris:Cert este că dacă x mai mic ca y mai mic ca z sunt numere naturale nenule atunci în mod sigur AD este un număr rațional mai mare ca zero.
Dar AD, nu AD^2.
Dacă x, y, z sunt întregi.
Dacă AD este rațional, sub formă de fracție ireductibila a/b, atunci AD^2 trebuie obligatoriu să fie cu numărătorul și numitorul pătrate perfecte.
Pentru a analiza coerent propunerea ta privind cazul că
1) - Relația de ordine între numerele naturale este
2) - Există următoarele relații
3) - Punctul
Dacă ești de-acord, atunci îți voi explica de ce am considerat că
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2602




Puncte : 22063
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Relatia asta a ta nu este buna. Nu verifica teorema lui Fermat . Ti-am demonstrat ca relatia mea este buna.Dacu a scris:
2) - Există următoarele relații.
.
CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12205




Puncte : 58171
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
De acord, Dacu.Dacu a scris:Deoarece tu ai considerat altă relație de ordine între laturile trunghiului și o altă poziție a punctuluicuriosul a scris:Dacă îmi demonstrezi asta, eu demonstrez restul.Dacu a scris:Cert este că dacă x mai mic ca y mai mic ca z sunt numere naturale nenule atunci în mod sigur AD este un număr rațional mai mare ca zero.
Dar AD, nu AD^2.
Dacă x, y, z sunt întregi.
Dacă AD este rațional, sub formă de fracție ireductibila a/b, atunci AD^2 trebuie obligatoriu să fie cu numărătorul și numitorul pătrate perfecte.situat în interiorul laturii
, atunci te rog să fii de-acord cu propunerile mele de mai jos.
Pentru a analiza coerent propunerea ta privind cazul căeste un număr natural prim ținând cont de Teorema lui Stewart în triunghiul
unde
, atunci trebuie să stabilim următoarele:
1) - Relația de ordine între numerele naturale este.
2) - Există următoarele relații.
3) - Punctuleste situat în interiorul laturii
unde
Dacă ești de-acord, atunci îți voi explica de ce am considerat căeste reprezentat de un număr natural.
De altfel din inegalitățile respective este suficient de arătat doar prima, x>n, restul rezultă din z>y>x.
Deci, de acord, continuă te rog.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Ca să implicăm și x, y, z ca soluții ale ecuației, eu mă gândeam azi, printre timp, să împărțim latura z în x^n/z^(n-1) și y^n/z^(n-1) aplicând relația lui Stewart, dar nu dă rezultate directe.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
CAdi a scris:Relatia asta a ta nu este buna. Nu verifica teorema lui Fermat . Ti-am demonstrat ca relatia mea este buna.Dacu a scris:
2) - Există următoarele relații.
.
Retrag ce am scris mai sus, si imi cer scuze , si relatiile lui Dacu verifica teorema lui Fermat. Este varianta pentru n= par
CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12205




Puncte : 58171
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Fii atent la o relație interesantă.
Dacă am calculat bine.
Îl extragi pe (p_y)^2 din prima și ar trebui să ajungi la ceva de genul:

După care îl extragi pe (p_x)^2 dintr-a doua relație și ar trebui să ajungi la ceva de genul:
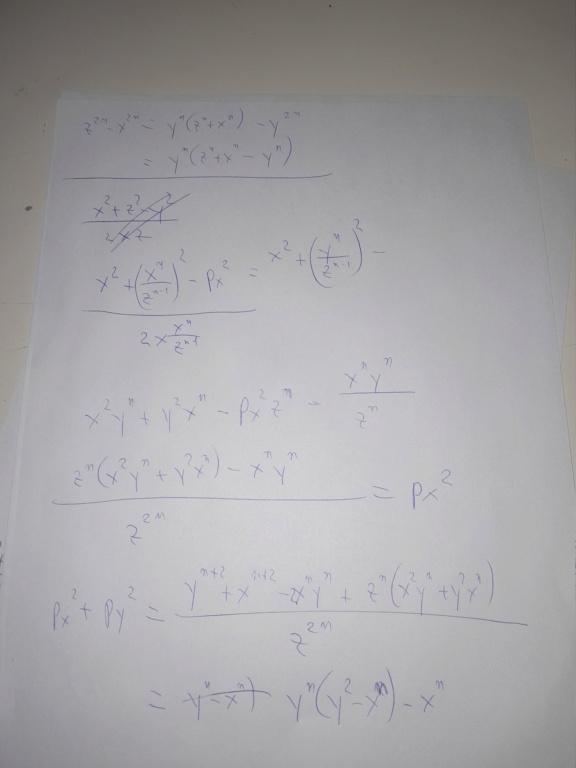
Faci suma lor, o înlocuiești în relația menționată anterior și ar trebuie să ajungi la o relație de genul:

De unde ar rezulta că
y^(n+2)+x^(n+2)- 2x^ny^n trebuie să fie divizibil cu z^2.
Și nu poate fi.
Dar asta doar dacă am calculat corect că n-am verificat.
Dacă am calculat bine.
Îl extragi pe (p_y)^2 din prima și ar trebui să ajungi la ceva de genul:

După care îl extragi pe (p_x)^2 dintr-a doua relație și ar trebui să ajungi la ceva de genul:
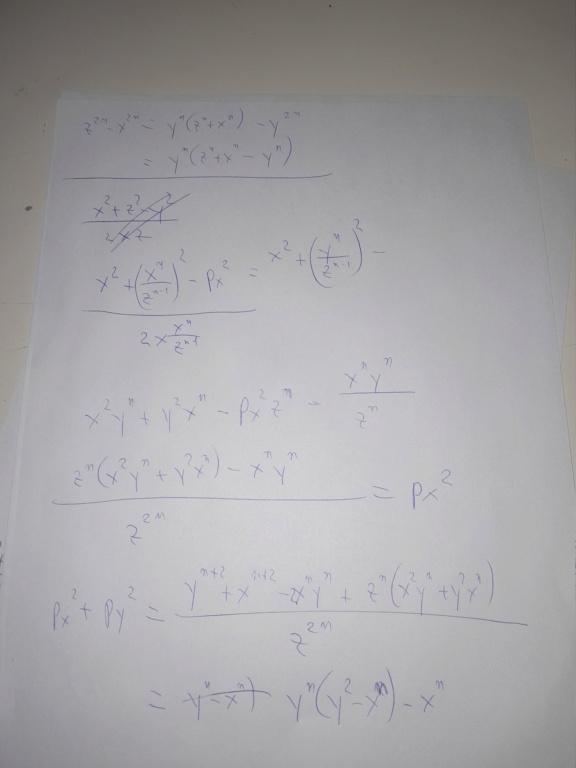
Faci suma lor, o înlocuiești în relația menționată anterior și ar trebuie să ajungi la o relație de genul:

De unde ar rezulta că
y^(n+2)+x^(n+2)- 2x^ny^n trebuie să fie divizibil cu z^2.
Și nu poate fi.
Dar asta doar dacă am calculat corect că n-am verificat.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Dar sigur e greșit ceva pe undeva, nici nu stau să verific, pentru că nu este departajat n de valoarea lui pentru 2 și ar însemna că trebuie să fie adevărat și pentru n=2 și nu este.
Dar oricum, tu poți să prezinți concluzia ta referitoare la AD rațional.
Dar oricum, tu poți să prezinți concluzia ta referitoare la AD rațional.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
N-am verificat, dar dacă în concluzia de mai sus ar fi greșit doar semnul lui 2x^ny^n , se poate arăta că
y^(n+2)+x^(n+2)+2x^ny^n este divizibil cu z^2, doar dacă n=2.
Dar mă îndoiesc că aici este greșeala.
y^(n+2)+x^(n+2)+2x^ny^n este divizibil cu z^2, doar dacă n=2.
Dar mă îndoiesc că aici este greșeala.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
M-am gandit si la o alta abordare a teoremei lui Fermat, dupa cea descrisa cu Binomul lui Newton.
Graficul functiei x^n+y^n este o functie pe care o putem scrie in 2 variante (a mea si a lui Dacu):
f(x)= x^n+(x+1)^n
sau
f(x) =(x+1)^n+ (x+2) ^n
la fel si graficul functiei z^n :
f(x) =(X+2)^n
sau
f(x)= (X+3)^n
Se stie ca functiile cu putere mai mare decat 3 deci n>3 au radacinile ecuatiilor la intersectia cu axele Ox si Oy in multimea numerelor reale si complexe.
Cum graficele celor 2 functii sunt total diferite , ma indoiesc ca vreuna din radacini dintr-o parte si din cealalta sa coincida vreodata in acelasi timp si sa fie si numar natural
Graficul functiei x^n+y^n este o functie pe care o putem scrie in 2 variante (a mea si a lui Dacu):
f(x)= x^n+(x+1)^n
sau
f(x) =(x+1)^n+ (x+2) ^n
la fel si graficul functiei z^n :
f(x) =(X+2)^n
sau
f(x)= (X+3)^n
Se stie ca functiile cu putere mai mare decat 3 deci n>3 au radacinile ecuatiilor la intersectia cu axele Ox si Oy in multimea numerelor reale si complexe.
Cum graficele celor 2 functii sunt total diferite , ma indoiesc ca vreuna din radacini dintr-o parte si din cealalta sa coincida vreodata in acelasi timp si sa fie si numar natural
CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12205




Puncte : 58171
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Deocamdată, CAdi, nu știu ce să zic, eu încerc o abordare cât mai elementară, bazată pe factorizare, atât timp cât x, y, z unt naturale.
Mai am o idee interesantă și o să o expun diseară.
Mai am o idee interesantă și o să o expun diseară.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Este irelevant să analizăm ecuația rezultată din Teorema lui Stewart fără a ține cont și de ecuațiacuriosul a scris:De acord, Dacu.Dacu a scris:Deoarece tu ai considerat altă relație de ordine între laturile trunghiului și o altă poziție a punctuluicuriosul a scris:
Dacă îmi demonstrezi asta, eu demonstrez restul.
Dar AD, nu AD^2.
Dacă x, y, z sunt întregi.
Dacă AD este rațional, sub formă de fracție ireductibila a/b, atunci AD^2 trebuie obligatoriu să fie cu numărătorul și numitorul pătrate perfecte.situat în interiorul laturii
, atunci te rog să fii de-acord cu propunerile mele de mai jos.
Pentru a analiza coerent propunerea ta privind cazul căeste un număr natural prim ținând cont de Teorema lui Stewart în triunghiul
unde
, atunci trebuie să stabilim următoarele:
1) - Relația de ordine între numerele naturale este.
2) - Există următoarele relații.
3) - Punctuleste situat în interiorul laturii
unde
Dacă ești de-acord, atunci îți voi explica de ce am considerat căeste reprezentat de un număr natural.
De altfel din inegalitățile respective este suficient de arătat doar prima, x>n, restul rezultă din z>y>x.
Deci, de acord, continuă te rog.
Să ne aducem aminte că din demonstrația mea din sistemul de ecuații
----------------------------------------------------------------------------------------------------------------
Fie
să aibă cel puțin o soluție
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2602




Puncte : 22063
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Absolut complet de acord cu tine.Dacu a scris:Este irelevant să analizăm ecuația rezultată din Teorema lui Stewart fără a ține cont și de ecuația Marea teorema a lui Fermat. - x^n+y^n=z^n
Poate, să zicem, ne-am putea folosi cumva de faptul că z-y are factor comun cu x, z-x are un factor comun cu y etc, dar nu ajută mai deloc.
Ne învârtim în cerc ajungând la egalități care nu se pot contrazice una pe alta.
Deci este inutil, intr-un final, dacă nu putem demonstra măcar că AD este rațional.
Dacă se poate demonstra că AD este rațional continuarea implicativa cred că știu cum s-o fac și funcționează, dar nu se poate demonstra asta, mai mult, cel mai probabil, AD este irațional.
Mi-am amintit și ce ai mai spus tu în continuare în mesajul tău și atâta le-am socotit azi la muncă în capul meu...doamne, nu mă mai puteam concentra la ce trebuie să fac în cadrul serviciului la un moment dat.
Le-am întors pe toate părțile posibile, nu duce la rezultate concrete, garantat.
Vezi că referitor la y^n-x^n=z^(n-2)(y^2-x^2) nu are cum să rezulte, noi doi am dezbătut mult această relație acum câțiva ani.
Dacă s-ar demonstra egalitatea, e joc de glezne să demonstrezi că nu poate fi valabilă pentru n>2, x, y, z, n naturale.
Adică eu îți pot arăta asta în două propoziții și o ecuație, că la nivel de primalitate, scriind y^n-x^n =z^n-2x^n, de exemplu, sau 2y^n-z^n, egalitatea pentru n>2 implică y și z, sau x și z, după caz, având factori comuni.
Dar nu poate rezulta asta nici din modul în care ai propus tu atunci folosind implicarea cosinusurilor prin relația ta.
Dacă vrei, reluam analiza, dar n-are rost.
Dar dacă, totuși vrei, putem s-o reluam.
În schimb, azi, tot sucindu-mi mintea în toate părțile, am găsit o chestiune interesantă referitoare la "simetria aia binomială" din celălalt subiect.
Încă analizez.
E ciudat de interesantă, dar nu știu încă cum să conectez lucrurile între ele.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
CAdi a scris:M-am gandit si la o alta abordare a teoremei lui Fermat, dupa cea descrisa cu Binomul lui Newton.
Graficul functiei x^n+y^n este o functie pe care o putem scrie in 2 variante (a mea si a lui Dacu):
f(x)= x^n+(x+1)^n
sau
f(x) =(x+1)^n+ (x+2) ^n
la fel si graficul functiei z^n :
f(x) =(X+2)^n
sau
f(x)= (X+3)^n
Se stie ca functiile cu putere mai mare decat 3 deci n>3 au radacinile ecuatiilor la intersectia cu axele Ox si Oy in multimea numerelor reale si complexe.
Cum graficele celor 2 functii sunt total diferite , ma indoiesc ca vreuna din radacini dintr-o parte si din cealalta sa coincida vreodata in acelasi timp si sa fie si numar natural
Si ipoteza mea este corecta , am facut graficele celor 2 functii si se vede ca cele 2 functii rezultate din teorema lui Fermat nu au radacini comune in multimea numerelor naturale ,
pentru puteri ale lui n>3 si deci Teorema lui Fermat:
,,Teorema: Ecuația x^{n}+y^{n}=z^{n} nu are soluții dacă n>2 este număr natural, iar x,y,z sunt numere naturale nenule"
este demonstrata si prin metoda graficelor de functii.

CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12205




Puncte : 58171
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
CAdi a scris:CAdi a scris:M-am gandit si la o alta abordare a teoremei lui Fermat, dupa cea descrisa cu Binomul lui Newton.
Graficul functiei x^n+y^n este o functie pe care o putem scrie in 2 variante (a mea si a lui Dacu):
f(x)= x^n+(x+1)^n
sau
f(x) =(x+1)^n+ (x+2) ^n
la fel si graficul functiei z^n :
f(x) =(X+2)^n
sau
f(x)= (X+3)^n
Se stie ca functiile cu putere mai mare decat 3 deci n>3 au radacinile ecuatiilor la intersectia cu axele Ox si Oy in multimea numerelor reale si complexe.
Cum graficele celor 2 functii sunt total diferite , ma indoiesc ca vreuna din radacini dintr-o parte si din cealalta sa coincida vreodata in acelasi timp si sa fie si numar natural
Si ipoteza mea este corecta , am facut graficele celor 2 functii si se vede ca cele 2 functii rezultate din teorema lui Fermat nu au radacini comune in multimea numerelor naturale ,
pentru puteri ale lui n>3 si deci Teorema lui Fermat:
,,Teorema: Ecuația x^{n}+y^{n}=z^{n} nu are soluții dacă n>2 este număr natural, iar x,y,z sunt numere naturale nenule"
este demonstrata si prin metoda graficelor de functii.
Si am si confirmarea :
Graficele celor doua functii din ecuatia generala care respecta Teorema lui Pitagora :
x^n + (x+1)^n = (x+2)^n
adica mai detaliat :
f(x) = x^n + (x+1)^n
si
g(x)=(x+2)^n
pentru n=2 , devin :
f(x) = x^2 + (x+1)^2
si
g(x)=(x+2)^2
si se intretaie (au radacini comune) in punctele -1 si 3 care sunt solutiile ecuatiei x^2 + (x+1)^2= (x+2)^2 asa cum am demonstrat anterior .

Iata si graficele functiilor corespunzatoare pentru ecuatia lui Dacu (x+1)^n+ (x+2) ^n= (x+3)^n
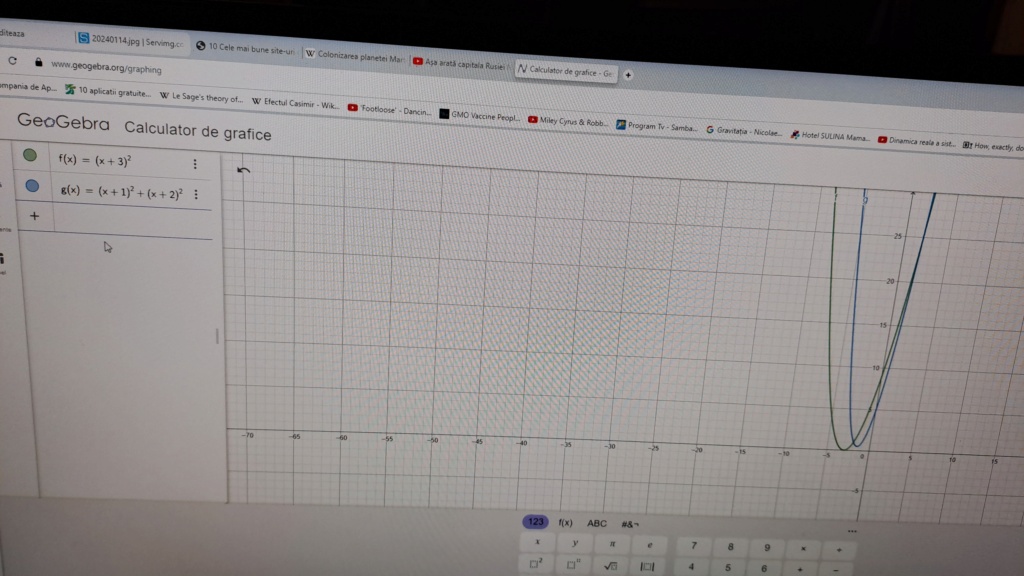
mai sus care are radacina comuna x=2 pentru f(x) =(x+1)^2+ (x+2) ^2 si g(x)= (x+3)^2 care verifica Teorema lui Pitagora.
si mai jos pentru n=4

unde nu exista radacini in multimea numerelor naturale pentru f(x) =(x+1)^4+ (x+2) ^4 si g(x)= (x+3)^4
Mai jos si graficul unor functii pentru n=26 pentru care la fel nu exista solutii in multimea numerelor naturale;

si un grafic curios pentru n= 999

CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12205




Puncte : 58171
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Bun, hai să mai și postez ceva, cel puțin până în locul unde am găsit o inconsistență.
Să vedem dacă poate fi corectată.
M-am chinuit între timp un pic, dar încă nu reușesc și eventual, o să revin cu continuarea ulterior dacă reușesc s-o clarific.
Până atunci prezint cam ce-am gândit și cum am gândit.












Să vedem dacă poate fi corectată.
M-am chinuit între timp un pic, dar încă nu reușesc și eventual, o să revin cu continuarea ulterior dacă reușesc s-o clarific.
Până atunci prezint cam ce-am gândit și cum am gândit.












curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Ideea este că în ambii termeni din egalitățile anterioare de pe ultima pagină am încercat să exprim o legătură de factorizare între modul în care este exprimat un număr de forma a*a1-b*b1=a*a2-b*b2.
Dar am greșit ceva undeva.
Nici nu știu dacă paginile le-am expus în ordine, dar dacă e să pot clarifica le reordonez eu.
Dar am greșit ceva undeva.
Nici nu știu dacă paginile le-am expus în ordine, dar dacă e să pot clarifica le reordonez eu.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Și menționez și asta poate mai da idei cuiva.
Am plecat de la ideea că dacă atât a-b, cât și c-d se divide ambele cu u, atunci ac-bd se divide cu u.
Am plecat de la ideea că dacă atât a-b, cât și c-d se divide ambele cu u, atunci ac-bd se divide cu u.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Urrra!!!!
Am găsit!
In ultima egalitate de pe ultima pagină, valoarea lui u este mai mare ca 1 și trebuie să fie un factor comun pentru (x_2^p + x^(p-1)) și x+z-y de unde rezultă că x_2 si x_1 au un factor comun.
De aici rezultă că x, y, z nu pot fi prime între ele.
Am găsit!
In ultima egalitate de pe ultima pagină, valoarea lui u este mai mare ca 1 și trebuie să fie un factor comun pentru (x_2^p + x^(p-1)) și x+z-y de unde rezultă că x_2 si x_1 au un factor comun.
De aici rezultă că x, y, z nu pot fi prime între ele.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Pentru a putea discuta coerent ceea ce ai scris trebuie să spui cărei mulțimi de numere aparțin numerele x,y,z căci evident n este un număr natural mai mare ca 3.curiosul a scris:Bun, hai să mai și postez ceva, cel puțin până în locul unde am găsit o inconsistență.
Să vedem dacă poate fi corectată.
M-am chinuit între timp un pic, dar încă nu reușesc și eventual, o să revin cu continuarea ulterior dacă reușesc s-o clarific.
Până atunci prezint cam ce-am gândit și cum am gândit.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2602




Puncte : 22063
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Deci, Dacule, ... parcă iar jucăm în filme diferite după cum te-ai exprimat.
Și repet, plecând de la tot ce am expus, se poate arăta că x_1 și x_2 trebuie să aibă un factor comun.
Dar, mă rog, nici nu mă obosesc să îți explic cum dacă asta a fost tot ce ai putut să spui.
Și repet, plecând de la tot ce am expus, se poate arăta că x_1 și x_2 trebuie să aibă un factor comun.
Dar, mă rog, nici nu mă obosesc să îți explic cum dacă asta a fost tot ce ai putut să spui.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Am recitit un pic și înțeleg ce te-a derutat și ce te-a făcut să te exprimi așa.
În multe locuri am folosit exprimarea este "intreg" și nu natural.
Dar este o chestiune personală de percepție și exprimare, întotdeauna asociind "întreg" cu "natural".
Adică un număr și cu mâini, și cu picioare, metaforic vorbind.
Un număr rațional eu îl văd ca pe un număr incomplet, din care lipsește ceva, asociind exprimarea de mai sus, iar un număr irațional îl văd ca pe un număr care nu își găsește niciun loc nicăieri.
Când m-am exprimat întreg, m-am exprimat la un număr din care nu lipsește ceva pentru a fi complet, nu pentru că aș fi vrut să extind în Z.
În sfârșit...
Ignoră exprimarea întreg și folosește natural.
E valabil și pentru p prim egal cu 3, nu doar mai mare ca 3, deși pentru n=3, dintr-o anumită perspectivă de analiză, apare o particularitate care nu se mai regăsește în niciun alt caz.
Este vorba de un fel de simetrie perfectă raportat la ecuația despre care vorbim.
În celelalte, mai apare câte ceva diferit, dar în cazul n=3 apare un fel de simetrie care te învârte în jurul cozii tot timpul în analiza ecuației.
În multe locuri am folosit exprimarea este "intreg" și nu natural.
Dar este o chestiune personală de percepție și exprimare, întotdeauna asociind "întreg" cu "natural".
Adică un număr și cu mâini, și cu picioare, metaforic vorbind.
Un număr rațional eu îl văd ca pe un număr incomplet, din care lipsește ceva, asociind exprimarea de mai sus, iar un număr irațional îl văd ca pe un număr care nu își găsește niciun loc nicăieri.
Când m-am exprimat întreg, m-am exprimat la un număr din care nu lipsește ceva pentru a fi complet, nu pentru că aș fi vrut să extind în Z.
În sfârșit...
Ignoră exprimarea întreg și folosește natural.
E valabil și pentru p prim egal cu 3, nu doar mai mare ca 3, deși pentru n=3, dintr-o anumită perspectivă de analiză, apare o particularitate care nu se mai regăsește în niciun alt caz.
Este vorba de un fel de simetrie perfectă raportat la ecuația despre care vorbim.
În celelalte, mai apare câte ceva diferit, dar în cazul n=3 apare un fel de simetrie care te învârte în jurul cozii tot timpul în analiza ecuației.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Deci x,y,z sunt numere naturale cu x mai mic ca y mai mic ca z și evident n este mai mare ca 2 (scuze că am spus mai mare ca 3).Dacă x și y sunt impare, atunci pot fi x și y simultan numere naturale prime?curiosul a scris:Am recitit un pic și înțeleg ce te-a derutat și ce te-a făcut să te exprimi așa.
În multe locuri am folosit exprimarea este "intreg" și nu natural.
Dar este o chestiune personală de percepție și exprimare, întotdeauna asociind "întreg" cu "natural".
Adică un număr și cu mâini, și cu picioare, metaforic vorbind.
Un număr rațional eu îl văd ca pe un număr incomplet, din care lipsește ceva, asociind exprimarea de mai sus, iar un număr irațional îl văd ca pe un număr care nu își găsește niciun loc nicăieri.
Când m-am exprimat întreg, m-am exprimat la un număr din care nu lipsește ceva pentru a fi complet, nu pentru că aș fi vrut să extind în Z.
În sfârșit...
Ignoră exprimarea întreg și folosește natural.
E valabil și pentru p prim egal cu 3, nu doar mai mare ca 3, deși pentru n=3, dintr-o anumită perspectivă de analiză, apare o particularitate care nu se mai regăsește în niciun alt caz.
Este vorba de un fel de simetrie perfectă raportat la ecuația despre care vorbim.
În celelalte, mai apare câte ceva diferit, dar în cazul n=3 apare un fel de simetrie care te învârte în jurul cozii tot timpul în analiza ecuației.
Vom discuta doar ce ai scris la punctul 1.Apoi vom discuta ce ai scris la punctul 2.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2602




Puncte : 22063
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
O mică corectare în ce ai spus, x și y nu sunt ambele impare, ci una pară, una impară pentru că z trebuie să fie obligatoriu impar.
Nu m-am gândit la asta, dar cred că este imposibil, pentru n prim impar ca una din soluții să fie număr prim.
Aș zice, la repezeală, pentru că x+y-z este nenul, dar nu cred că așa se explică clar de ce niciuna nu poate fi număr prim.
În schimb, analizand acum pe moment, dacă x ar fi prim, z-y=1, sau dacă y ar fi prim, z-x=1, iar ecuația s-ar reduce la x, y, și y+1 sau x, y și x+1.
Dar pentru n prim impar, că despre asta este vorba acum, x+y și y+1 trebuie să aibă un factor comun, factor care trebuie să apară și în x-1.
Dar asta înseamnă că acest factor trebuie să se regăsească și în xy prin dezvoltarea x^p+y^p din factorul din paranteza mare, iar acesta nu poate fi decât p.
Nu știu cât e de corect, că sunt făcute acuma imaginar pe moment, dar nu știu nici câtă relevanță are acum.
Nu m-am gândit la asta, dar cred că este imposibil, pentru n prim impar ca una din soluții să fie număr prim.
Aș zice, la repezeală, pentru că x+y-z este nenul, dar nu cred că așa se explică clar de ce niciuna nu poate fi număr prim.
În schimb, analizand acum pe moment, dacă x ar fi prim, z-y=1, sau dacă y ar fi prim, z-x=1, iar ecuația s-ar reduce la x, y, și y+1 sau x, y și x+1.
Dar pentru n prim impar, că despre asta este vorba acum, x+y și y+1 trebuie să aibă un factor comun, factor care trebuie să apară și în x-1.
Dar asta înseamnă că acest factor trebuie să se regăsească și în xy prin dezvoltarea x^p+y^p din factorul din paranteza mare, iar acesta nu poate fi decât p.
Nu știu cât e de corect, că sunt făcute acuma imaginar pe moment, dar nu știu nici câtă relevanță are acum.
Ultima editare efectuata de catre curiosul in Vin 16 Feb 2024, 21:56, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
În schimb, că nu am fost atent, cu siguranță și certitudine nu pot fi ambele prime.
Tu cred că te referi mai degrabă la cele două soluțiile impare ale ecuației, dar ambele nu pot fi prime în niciun caz.
Poate doar una dintre ele, dar ambele sigur nu.
Și că ambele soluții impare nu pot fi numere prime îți demonstrez lejer că nu este posibil.
Poate doar una dintre ele.
Pentru n număr prim impar.
Tu cred că te referi mai degrabă la cele două soluțiile impare ale ecuației, dar ambele nu pot fi prime în niciun caz.
Poate doar una dintre ele, dar ambele sigur nu.
Și că ambele soluții impare nu pot fi numere prime îți demonstrez lejer că nu este posibil.
Poate doar una dintre ele.
Pentru n număr prim impar.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
De fapt, nu, m-am răzgândit, pentru n prim impar NICIUNA din soluții nu poate fi număr prim.
Demonstrabil.
Dar aici nu folosește acest aspect.
Îți arăt cum se demonstrează doar dacă te ajută pe tine cu ceva.
Aducând ecuația la o formă congruenta mod p.
Demonstrabil.
Dar aici nu folosește acest aspect.
Îți arăt cum se demonstrează doar dacă te ajută pe tine cu ceva.
Aducând ecuația la o formă congruenta mod p.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Și demonstrația e chiar frumoasă.
Ar merita menționată.
Are la bază un aspect menționat în simetria aia binomială.
Ar merita menționată.
Are la bază un aspect menționat în simetria aia binomială.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Uite, Dacule, de exemplu, cum se demonstrează că z nu poate fi un număr prim pentru n număr prim impar de asemenea.




Pentru cazul în care considerăm că una din soluțiile x sau y este un număr prim demonstrația ușor diferită dar mai simplă pentru că se ajunge la arăta că fie z-y=1, fie z-x=1.
Dacă vrei ți-o scriu și pe aceea.




Pentru cazul în care considerăm că una din soluțiile x sau y este un număr prim demonstrația ușor diferită dar mai simplă pentru că se ajunge la arăta că fie z-y=1, fie z-x=1.
Dacă vrei ți-o scriu și pe aceea.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
 Re: Marea teorema a lui Fermat.
Re: Marea teorema a lui Fermat.
Dar, Dacule, uite o altă chestiune interesantă pornind de la modul în care am analizat primalitatea pentru cazul x sau y, reproducând principiul la soluțiile x, y, z ale ecuației.
Cu alte cuvinte, pentru n impar, (x+y) este factorul lui z^n, ceea ce înseamnă că x+y nu poate avea alți factori diferiți de ai lui z.
Îl scriem pe x+y sub formă z+(x+y-z) de unde rezultă că z+(x+y-z) nu poate avea alți factori diferiți de ai lui z.
La fel de bine, x+y poate fi scris sub forma 2z-[z-(x+y-z)] expresie care nu poate avea factori diferiți de cei ai lui z.
În consecință, se ajunge la faptul că
atât z-(x+y-z) cât și z+(x+y-z)
nu pot avea factori diferiți de ai lui z, de unde s-ar putea trage concluzia că x+y-z nu poate avea alți factori diferiți de cei ai lui z.
Dar x+y-z are în factorizare un factor al lui x și un factor al lui y.
În aceeași ordine de idei, ar implica că x, y, z trebuie să conțină fiecare un factor al lui z.
Dar este undeva o chestiune de interpretare în 2z-[z-(x+y-z)] și să văd dacă poate fi fructificată la nivel de factorizare astfel încât să poată duce la această concluzie.
Cu alte cuvinte, pentru n impar, (x+y) este factorul lui z^n, ceea ce înseamnă că x+y nu poate avea alți factori diferiți de ai lui z.
Îl scriem pe x+y sub formă z+(x+y-z) de unde rezultă că z+(x+y-z) nu poate avea alți factori diferiți de ai lui z.
La fel de bine, x+y poate fi scris sub forma 2z-[z-(x+y-z)] expresie care nu poate avea factori diferiți de cei ai lui z.
În consecință, se ajunge la faptul că
atât z-(x+y-z) cât și z+(x+y-z)
nu pot avea factori diferiți de ai lui z, de unde s-ar putea trage concluzia că x+y-z nu poate avea alți factori diferiți de cei ai lui z.
Dar x+y-z are în factorizare un factor al lui x și un factor al lui y.
În aceeași ordine de idei, ar implica că x, y, z trebuie să conțină fiecare un factor al lui z.
Dar este undeva o chestiune de interpretare în 2z-[z-(x+y-z)] și să văd dacă poate fi fructificată la nivel de factorizare astfel încât să poată duce la această concluzie.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41197
Data de inscriere : 22/03/2011
Pagina 12 din 13 •  1, 2, 3 ... , 11, 12, 13
1, 2, 3 ... , 11, 12, 13 
 Subiecte similare
Subiecte similare» Alte aspecte privind teorema lui Fermat
» O demonstrație elementară pentru Marea teoremă a lui Fermat
» Mica teoremă a lui Fermat
» O demonstrație elementară pentru Marea teoremă a lui Fermat
» Mica teoremă a lui Fermat
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 12 din 13
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum|
|
|




 Devino fan Forumgratuit
Devino fan Forumgratuit 

