Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de ilasus Astazi la 19:58
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la No_name în Ce anume "generează" legile fizice?
( 1 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 1 )
» Mesaj de la Abel Cavaşi în Daci nemuritori
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| Dacu2 | ||||
| eugen | ||||
| Forever_Man | ||||
| Abel Cavaşi | ||||
| Meteorr |
Cei mai activi postatori ai saptamanii
| virgil | ||||
| Forever_Man | ||||
| Dacu2 | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Meteorr | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 28 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 28 Vizitatori Nici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Alte aspecte privind teorema lui Fermat
4 participanți
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 1 din 2
Pagina 1 din 2 • 1, 2 
 Alte aspecte privind teorema lui Fermat
Alte aspecte privind teorema lui Fermat
Provine din topicul „O problema de geometrie”.
Da Orakle, frumos demonstrat, felicitări !
Am analizat un pic ce ai scris, am mai citit câte ceva și de prin trigonometrie și am găsit o relație trigonometrică foarte frumoasă care implică Marea teoremă a lui Fermat, relație de implicare ce are de asemenea o demonstrație superbă. Mă refer doar la demonstrația relației de implicare a teoremei, nu a demonstrației teoremei propriu-zise. Nu am timp acum s-o scriu dar o voi face curând pentru că merită și cred că am găsit și niște relații trigonometrice noi între laturile unui triunghi.
Și anume.
Soluțiile x, y, z ale ecuației trebuie să fie întregi pozitive, prime între ele și să fie laturile unui triunghi.
Plecând de la triunghi, relația de implicare este :
Ecuația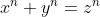 are soluții întregi pozitive, dacă
are soluții întregi pozitive, dacă 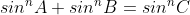 , unde A este unghiul format de x și z, B este unghiul format de y și z, iar C este unghiul format de x și y.
, unde A este unghiul format de x și z, B este unghiul format de y și z, iar C este unghiul format de x și y.
În consecință, putem ajunge la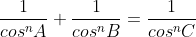 unde putem înlocui valorile cosinusurilor prin valorile determinate de teorema cosinusului și vedem ce rezultă.
unde putem înlocui valorile cosinusurilor prin valorile determinate de teorema cosinusului și vedem ce rezultă.
Nu am mai avut timp aseară să mai continuu, dar cred că o voi face în seara asta și să văd la ce rezultat mai ajung.
Tu ai vreo idee, plecând de aici ?
Voi prezenta și demonstrația relației de implicare.
Este superbă !
Da Orakle, frumos demonstrat, felicitări !
Am analizat un pic ce ai scris, am mai citit câte ceva și de prin trigonometrie și am găsit o relație trigonometrică foarte frumoasă care implică Marea teoremă a lui Fermat, relație de implicare ce are de asemenea o demonstrație superbă. Mă refer doar la demonstrația relației de implicare a teoremei, nu a demonstrației teoremei propriu-zise. Nu am timp acum s-o scriu dar o voi face curând pentru că merită și cred că am găsit și niște relații trigonometrice noi între laturile unui triunghi.
Și anume.
Soluțiile x, y, z ale ecuației trebuie să fie întregi pozitive, prime între ele și să fie laturile unui triunghi.
Plecând de la triunghi, relația de implicare este :
Ecuația
În consecință, putem ajunge la
Nu am mai avut timp aseară să mai continuu, dar cred că o voi face în seara asta și să văd la ce rezultat mai ajung.
Tu ai vreo idee, plecând de aici ?
Voi prezenta și demonstrația relației de implicare.
Este superbă !
Ultima editare efectuata de catre Abel Cavaşi in Mar 26 Aug 2014, 20:37, editata de 1 ori (Motiv : Provine din topicul...)
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Inițial formula la care ajunsesem și relația de implicare cu Marea teoremă a lui Fermat am găsit-o plecând de la formula lui Heron pentru aflarea ariei, dar am găsit una și mai simplă.
Folosind formula sinusului (catetă opusă supra ipotenuză) și cea pentru aflarea ariei într-un triunghi,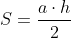 ajungem să stabilim generalizat că aria unui triunghi este :
ajungem să stabilim generalizat că aria unui triunghi este :
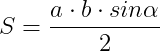
unde alfa este unghiul format de cele două laturi ale triunghiului.
Procedând identic pentru celelalte înălțimi, ajungem la relația :
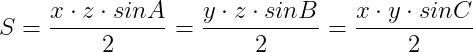
unde A, B, C sunt unghiurile formate de laturile x și z ale triunghiului, y și z și respectiv x și y, ceea ce duce la o constantă între laturile unui triunghi :
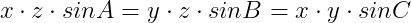
În continuare, putem găsi și o relație între raportul a două laturi ale triunghiului :
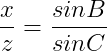
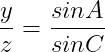
unde unghiurile A,B și C sunt cele menționate mai sus.
Plecând de relația de mai sus și raportat la ecuația lui Fermat, pe care o putem de asemenea scrie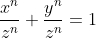 , folosind raporturile determinate mai sus pentru triunghi :
, folosind raporturile determinate mai sus pentru triunghi :
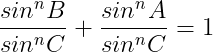
și implicit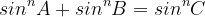
Cum sinusul unui unghi este inversul cosinusului acelui unghi, înlocuind mai sus ajungem la :
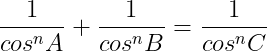
și înlocuind valorile determinate de teorema cosinusului trebuie să găsim soluțiile x, y, z întregi pozitive și prime între ele care satisfac relația :
^n}{\left&space;(z^2+x^2-y^2&space;\right&space;)^n}+&space;\frac{\left&space;(&space;2yz&space;\right&space;)^n}{\left&space;(z^2+y^2-x^2&space;\right&space;)^n}=\frac{\left&space;(&space;2xy&space;\right&space;)^n}{\left&space;(x^2+x^2-z^2&space;\right&space;)^n})
analizat în paralel cu faptul că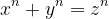
Folosind formula sinusului (catetă opusă supra ipotenuză) și cea pentru aflarea ariei într-un triunghi,
unde alfa este unghiul format de cele două laturi ale triunghiului.
Procedând identic pentru celelalte înălțimi, ajungem la relația :
unde A, B, C sunt unghiurile formate de laturile x și z ale triunghiului, y și z și respectiv x și y, ceea ce duce la o constantă între laturile unui triunghi :
În continuare, putem găsi și o relație între raportul a două laturi ale triunghiului :
unde unghiurile A,B și C sunt cele menționate mai sus.
Plecând de relația de mai sus și raportat la ecuația lui Fermat, pe care o putem de asemenea scrie
și implicit
Cum sinusul unui unghi este inversul cosinusului acelui unghi, înlocuind mai sus ajungem la :
și înlocuind valorile determinate de teorema cosinusului trebuie să găsim soluțiile x, y, z întregi pozitive și prime între ele care satisfac relația :
analizat în paralel cu faptul că
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
In mare nu am ce sa comentez.Asa la prima vedere nu vad nici o problema.Desi la introducerea relatilor in Fermat ar trebui sa intrii un pic in detalii.
Apoi ajung la fraza:
Cum sinusul unui unghi este inversul cosinusului acelui unghi, înlocuind mai sus ajungem la :...
Aici nu imi este clar ce vrei sa spui.
Apoi ajung la fraza:
Cum sinusul unui unghi este inversul cosinusului acelui unghi, înlocuind mai sus ajungem la :...
Aici nu imi este clar ce vrei sa spui.
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
orakle a scris:
Cum sinusul unui unghi este inversul cosinusului acelui unghi, înlocuind mai sus ajungem la :...
Aici nu imi este clar ce vrei sa spui.
Păi, în principiu
Sau mă înșel ?
Dacă mă înșel trebuie să reiau aproape tot, sau să exprimăm sinusul unui unghi doar în funcție de laturile acestuia.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
curiosul a scris:
Sau mă înșel ?
Dacă mă înșel trebuie să reiau aproape tot, sau să exprimăm sinusul unui unghi doar în funcție de laturile acestuia.
Te inseli si inca rau de tot !
Ultima editare efectuata de catre orakle in Dum 24 Aug 2014, 15:49, editata de 1 ori
Vizitator- Vizitator
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
curiosul a scris:
Folosind formula sinusului (catetă opusă supra ipotenuză) și cea pentru aflarea ariei într-un triunghi,ajungem să stabilim generalizat că aria unui triunghi este :
unde alfa este unghiul format de cele două laturi ale triunghiului.
Procedând identic pentru celelalte înălțimi, ajungem la relația :
unde A, B, C sunt unghiurile formate de laturile x și z ale triunghiului, y și z și respectiv x și y, ceea ce duce la o constantă între laturile unui triunghi :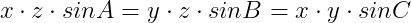
Deja, analizând un pic la repezeală, cred că putem ajunge la o relație între laturile x, y,z ale triunghiului doar plecând de la ultima egalitate la care s-a ajuns, stabilind anumite condiții care trebuie să le satisfacă laturile triunghiului x, y, z, ca să poată fi prime între ele și să vedem ulterior cum se poate folosi aceasta pentru ecuația lui Fermat.
În principiu, Orakle, este corect să exprimăm egalitatea :
plecând de la cea de mai sus ?
Dacă da, înlocuind valoarea pentru sinus obținută din
Dar o să analizez mai bine diseară, cu pixul pe hârtie, ca să nu-mi scape ceva.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Se pot găsi exprimări ale sinusurilor în funcție de laturile triunghiului, dar nu prea mă ajută la ce vreau eu :
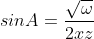 ;
; 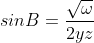 ;
; 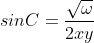
unde omega poate avea trei exprimări diferite, dar egale :
![\omega =\left [ \left ( x+y \right )^2-z^2 \right ]\left [z^2- \left ( y-x \right )^2 \right ]](http://latex.codecogs.com/gif.latex?\omega&space;=\left&space;[&space;\left&space;(&space;x+y&space;\right&space;)^2-z^2&space;\right&space;]\left&space;[z^2-&space;\left&space;(&space;y-x&space;\right&space;)^2&space;\right&space;])
![\omega =\left [ \left ( z+y \right )^2-x^2 \right ]\left [x^2- \left ( z-y \right )^2 \right ]](http://latex.codecogs.com/gif.latex?\omega&space;=\left&space;[&space;\left&space;(&space;z+y&space;\right&space;)^2-x^2&space;\right&space;]\left&space;[x^2-&space;\left&space;(&space;z-y&space;\right&space;)^2&space;\right&space;])
![\omega =\left [ \left ( z+x \right )^2-y^2 \right ]\left [y^2- \left ( z-x \right )^2 \right ]](http://latex.codecogs.com/gif.latex?\omega&space;=\left&space;[&space;\left&space;(&space;z+x&space;\right&space;)^2-y^2&space;\right&space;]\left&space;[y^2-&space;\left&space;(&space;z-x&space;\right&space;)^2&space;\right&space;])
Dar altceva, vis-a-vis de o legătură între x, y, z, întregi cu condiția să fie prime între ele nu pot găsi.
Deocamdată...
unde omega poate avea trei exprimări diferite, dar egale :
Dar altceva, vis-a-vis de o legătură între x, y, z, întregi cu condiția să fie prime între ele nu pot găsi.
Deocamdată...
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
curiosul a scris:Se pot găsi exprimări ale sinusurilor în funcție de laturile triunghiului, dar nu prea mă ajută la ce vreau eu :;
;
unde omega poate avea trei exprimări diferite, dar egale :
Dar altceva, vis-a-vis de o legătură între x, y, z, întregi cu condiția să fie prime între ele nu pot găsi.
Deocamdată...
Și totuși se poate, analizat prin faptul că pentru n impar, dacă
Analizând ecuațiile
cu u real, ceea ce duce la o concluzie interesantă.
Voi detalia diseară.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Nu este nici o graba.Gandeste de doua ori si scrie o singura data.
Pana pe data de 10 sept nu stiu ce net o sa am.Ne mai auzim dupa.
Pana pe data de 10 sept nu stiu ce net o sa am.Ne mai auzim dupa.
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
orakle a scris:Nu este nici o graba.Gandeste de doua ori si scrie o singura data.
Ai dreptate.
Deja, din grabă, am văzut că în a doua ecuație a sistemului apare y, și nu trebuie să apară.
Sistemul corect este
unde x'x"=x, y'y"=y si z'z"=z.
Oricum, o să încerc să analizez bine tot și să scriu o singură dată.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Alte aspecte privind teorema lui Fermat
Alte aspecte privind teorema lui Fermat
Rog un administrator sau moderator dacă poate muta ceea ce am scris eu și nu are relevanță cu problema referitoare la triunghi, ci cu teorema lui Fermat, să mute postările respective într-un alt topic, pentru că voi continua acolo, dacă se consideră cu nu este o chestie geometrică și nu are legătură cu subiectul.
Pentru că, într-adevăr, nu m-am înșelat și aș vrea să continui subiectul, pentru că se ajunge la un aspect interesant printr-o analiză trigonometrică a teoremei lui Fermat.
Pentru că, într-adevăr, nu m-am înșelat și aș vrea să continui subiectul, pentru că se ajunge la un aspect interesant printr-o analiză trigonometrică a teoremei lui Fermat.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Mulțumesc Abel !
Orakle, mai este o chestie asupra căreia vreau să fim amândoi de acord.
Să presupunem că avem egalitatea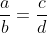
Este adevărat că, de asemenea, este adevărată și egalitatea (?)
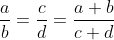
Dacă este corect, atunci trebuie să avem și
^n=\left&space;(\frac{c}{d}&space;\right&space;)^n=\left&space;(\frac{a+b}{c+d}&space;\right&space;)^n=\frac{a^n+b^n}{c^n+d^n})
ultima egalitate^n}{(c+d)^n}=\frac{a^n+b^n}{c^n+d^n}) fiind cea care mă interesează de fapt.
fiind cea care mă interesează de fapt.
Este corect până aici ?
Orakle, mai este o chestie asupra căreia vreau să fim amândoi de acord.
Să presupunem că avem egalitatea
Este adevărat că, de asemenea, este adevărată și egalitatea (?)
Dacă este corect, atunci trebuie să avem și
ultima egalitate
Este corect până aici ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Scuze Orakle, rectific, am încurcat un pic b cu c.
Corectez în citat :
Corectez în citat :
curiosul a scris:
Orakle, mai este o chestie asupra căreia vreau să fim amândoi de acord.
Să presupunem că avem egalitatea.
Este adevărat că, de asemenea, este adevărată și egalitatea?
Dacă este corect, atunci trebuie să avem și
ultima egalitatefiind cea care mă interesează de fapt.
Este corect până aici ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Păi Orakle, eu am gândit așa.
Dacă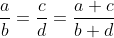
atunci, prin aceeași logică trebuie să avem și
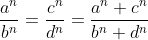
Dar cum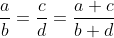 , ridicând fiecare membru la puterea n rezultă că
, ridicând fiecare membru la puterea n rezultă că
^n}{\left&space;(&space;b+d&space;\right&space;)^n})
Înțelegi ce vreau să spun ?
Să nu uităm că întotdeauna avem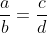
Dacă
atunci, prin aceeași logică trebuie să avem și
Dar cum
Înțelegi ce vreau să spun ?
Să nu uităm că întotdeauna avem
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Vorbim de raport Orakle, nu de egalitate.
Deci nu vorbim de (a+b)^2 egal cu a^2+b^2.
Înțelegi ce vreau să spun ?
Este corectă concluzia :
curiosul a scris:Dacă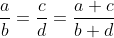
atunci, prin aceeași logică trebuie să avem și
Dar cum, ridicând fiecare membru la puterea n rezultă că
Înțelegi ce vreau să spun ?
Să nu uităm că întotdeauna avem
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Ha ha ha !!
Intradevar asa este cum zici.
Pare ciudat rezultatul dar este corect.


Intradevar asa este cum zici.
Pare ciudat rezultatul dar este corect.
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Ok, mă bucur că am confirmarea ta.
Restul cred că îți explic mâine.
Mai verific o dată, așa cum ai spus, analizează de două ori și scrie o dată.
Rezultatul este destul de interesant, zic eu, dacă calculele sunt corecte.
O seară bună Orakle !
Restul cred că îți explic mâine.
Mai verific o dată, așa cum ai spus, analizează de două ori și scrie o dată.
Rezultatul este destul de interesant, zic eu, dacă calculele sunt corecte.
O seară bună Orakle !
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
curiosul a scris:Ok, mă bucur că am confirmarea ta.
Restul cred că îți explic mâine.
Mai verific o dată, așa cum ai spus, analizează de două ori și scrie o dată.
Rezultatul este destul de interesant, zic eu, dacă calculele sunt corecte.
O seară bună Orakle !
Calculele eu zic ca sunt corecte.Problema este ca egalitatea
Maine daca o sa am net o sa-ti trimit un link cu o demonstratie frumoasa (ceva legat de numere prime) E f frumoasa si poate iti este de ajutor.
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Nu este nimic ciudat!Rezultatul este corect deoarece este o axiomă Este o axiomă că dacăorakle a scris:Ha ha ha !!
Intradevar asa este cum zici.
Pare ciudat rezultatul dar este corect.


Ce cercetare mai e şi asta!!!!????Te ştiu om serios!
Cred că şi tu ar trebui sa mai analizezi de două,trei,patru,etc. ori si după aceea să postezi un răspuns!
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Dacu a scris:Nu este nimic ciudat!Rezultatul este corect deoarece este o axiomă Este o axiomă că dacăorakle a scris:Ha ha ha !!
Intradevar asa este cum zici.
Pare ciudat rezultatul dar este corect.


atunci
şi evident că
.Mare descoperire,mare şi ingenioasă pe care şi un copil de clasa IV-a (sau unul de clasa III-a maiisteţ) o ştie ca pe o axiomă!2=2 şi deci 2x2=2x2 , 2x2x2=2x2x2 şi etc.............



Ce cercetare mai e şi asta!!!!????Te ştiu om serios!
Cred că şi tu ar trebui sa mai analizezi de două,trei,patru,etc. ori si după aceea să postezi un răspuns!
@Dacu

Nu la relatia respectiva m-am referit cand am spus ca este ciudata dar corecta.
Citeste cu atentie.M-am referit la asta:
Vorba ta :
Si care este marea problema? Este "cercetare" la nivelul clasei a III. Cineva trebuie sa o faca si pe asta!
 Fata de alte subiecte de pe acest forum subiectele de matematica deschise ale lui Curiosul pot fi denumite"cercetare fundamentala".Macar au o logica au cap si au coada !
Fata de alte subiecte de pe acest forum subiectele de matematica deschise ale lui Curiosul pot fi denumite"cercetare fundamentala".Macar au o logica au cap si au coada !Mai bine ma distrez cu astea decat sa ma enervez cu visele tampe ale unora. Ce vrei sa tot postez spermatozoizi la posturile lui Abel ?

@Curiosul
Vezi asta:
http://primes.utm.edu/notes/proofs/Theorem2.html
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Nu este nimic ciudat!Tot o axiomă este şi relaţia rezultantă!Ce mare descoperire,mare???!!!orakle a scris:Nu la relatia respectiva m-am referit cand am spus ca este ciudata dar corecta.
Citeste cu atentie.M-am referit la asta:
Vorba ta :


Si care este marea problema? Este "cercetare" la nivelul clasei a III. Cineva trebuie sa o faca si pe asta!Fata de alte subiecte de pe acest forum subiectele de matematica deschise ale lui Curiosul pot fi denumite"cercetare fundamentala".Macar au o logica au cap si au coada !
Mai bine ma distrez cu astea decat sa ma enervez cu visele tampe ale unora. Ce vrei sa tot postez spermatozoizi la posturile lui Abel ?
Mai degrabă postezi la teoria elicoidală a lui Abel decât să vorbeşti ca să vorbeşti despre un şir de rapoarte egale la care există proprietăţi axiomatice ştiute şi de un copil isteţ de clasa III-a...
Îţi doresc multă distracţie la acest subiect tocit...Mai bine te duci pe muntele Tâmpa ca ai ce vedea...
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Multumesc de urari Dacule ! S-a racit vremea nu e loc de excursii in munti.Desi as pleca cu cea mai mare viteza.
Eu personal nu am auzit de axiomele astea poate ma ajuti cu un link.
Nu am auzit din cauza ca pe mine m-au inscris direct in a V-a asa istet am fost.



De ce sa postez la Abel ? Ii vrei raul ?
Vrei sa moara de suparare ?

 Il las o saptamana liber la batut campii .Sincer merita si el atata liniste.
Il las o saptamana liber la batut campii .Sincer merita si el atata liniste.
PS
Cum mai stai cu problema de geometrie de mai jos ?
Cauta o axioma ceva... si rezolva cate ceva la ea. Nu o lasa de izbeliste ca se razbuna!


Eu personal nu am auzit de axiomele astea poate ma ajuti cu un link.
Nu am auzit din cauza ca pe mine m-au inscris direct in a V-a asa istet am fost.
De ce sa postez la Abel ? Ii vrei raul ?
Vrei sa moara de suparare ?
PS
Cum mai stai cu problema de geometrie de mai jos ?
Cauta o axioma ceva... si rezolva cate ceva la ea. Nu o lasa de izbeliste ca se razbuna!
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Caută pe internet sir de rapoarte egale.........orakle a scris:Multumesc de urari Dacule ! S-a racit vremea nu e loc de excursii in munti.Desi as pleca cu cea mai mare viteza.
Eu personal nu am auzit de axiomele astea poate ma ajuti cu un link.
Nu am auzit din cauza ca pe mine m-au inscris direct in a V-a asa istet am fost.

De ce sa postez la Abel ? Ii vrei raul ?
Vrei sa moara de suparare ?

Il las o saptamana liber la batut campii .Sincer merita si el atata liniste.
PS
Cum mai stai cu problema de geometrie de mai jos ?
Cauta o axioma ceva... si rezolva cate ceva la ea. Nu o lasa de izbeliste ca se razbuna!

Teoria elicoidală a universului este o idee şi oricum este posibil să fie adevărată şi deci este mai interesant de discutat această teorie decât alte aşa zise probleme de matematică celebre pe care unii vor să le rezolve fără a cunoaşte axiomele din orice domeniu al matematicii.....
Care problemă de geometrie???Dacă vorbeşti de problema cu triunghiul şi şirul de rapoarte egale atunci aia nu este o problemă pentru că de fapt este o axiomă!!!!De ce nu vrei să fii serios???
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Io zic asahe, Dacii or fost primi care or inventat Teorema lu Fermat si Fermat o fost plagiator.Experienta recenta ne arata ca Romanii, urmashi Dacilor sunt Miezul Pamantului!
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Pacalici a scris:Io zic asahe, Dacii or fost primi care or inventat Teorema lu Fermat si Fermat o fost plagiator.Experienta recenta ne arata ca Romanii, urmashi Dacilor sunt Miezul Pamantului!
Si normal.
Exista si o axioma prin care se sustine asta.Axioma de pe vremea Dacilor.
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Da Dacule, matematică de clasa a treia, nu comentez nimic aici, pentru că mai mult nici nu-mi permite pregătirea pe care o am.
Însă, deși e de clasa a treia, se pare că eu știu să o aplic mai bine ca tine.
Folosind matematica asta de clasa a treia am reușit să arăt că dacă într-un triunghi este adevărat faptul că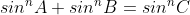 atunci trebuie obligatoriu să fie adevărată și egalitatea
atunci trebuie obligatoriu să fie adevărată și egalitatea ^n) ,
,
bazat în principiu pe faptul că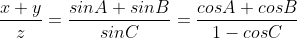
Dar am găsit un raționament și mai simplu, care duce cumva la același rezultat cu acesta de mai sus, dar pentru care ar trebui să scriu ceva mai mult, și care-i este adresat lui Orakle, deoarece nivelul tău superior nu acceptă soluții simple pentru probleme care sunt totuși ceva mai complicate.
Așadar Orakle, spune-mi te rog părerea la mesajul pe care-l voi scrie în continuare. O să încerc să simplific cât pot. Am ajuns la acest rezultat prin mai multe modalități diferite, ceea ce îmi spune că est puțin probabil să fie greșit. Dar oricum, să vedem ce-am mai găsit.
Însă, deși e de clasa a treia, se pare că eu știu să o aplic mai bine ca tine.
Folosind matematica asta de clasa a treia am reușit să arăt că dacă într-un triunghi este adevărat faptul că
bazat în principiu pe faptul că
Dar am găsit un raționament și mai simplu, care duce cumva la același rezultat cu acesta de mai sus, dar pentru care ar trebui să scriu ceva mai mult, și care-i este adresat lui Orakle, deoarece nivelul tău superior nu acceptă soluții simple pentru probleme care sunt totuși ceva mai complicate.
Așadar Orakle, spune-mi te rog părerea la mesajul pe care-l voi scrie în continuare. O să încerc să simplific cât pot. Am ajuns la acest rezultat prin mai multe modalități diferite, ceea ce îmi spune că est puțin probabil să fie greșit. Dar oricum, să vedem ce-am mai găsit.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
Pagina 1 din 2 • 1, 2 
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 1 din 2
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 
