Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Meteorr Ieri la 21:34
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Joi 21 Noi 2024, 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la Abel Cavaşi în ChatGPT este din ce în ce mai receptiv
( 1 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 1 )
» Mesaj de la virgil în Ce anume "generează" legile fizice?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Dacu2 | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Abel Cavaşi |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| virgil | ||||
| Dacu2 | ||||
| CAdi | ||||
| Meteorr | ||||
| ilasus | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 36 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 36 Vizitatori :: 1 Motor de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
O problema de geometrie
5 participanți
Pagina 1 din 1
 O problema de geometrie
O problema de geometrie
Se poate o idee la o problemă căreia nu i-am putut demonstraţia?
Fie ABCD paralelogram, în planul P, astfel încât AB paralelă cu DC si AD paralelă cu BC.
Fie un punct E, în planul P, astfel încât dreapta EC este perpendiculară pe BC în punctul C şi EA perpendiculară pe AB în punctul A.
Să se demonstreze că dreapta ED este perpendiculară pe diagonala AC a paralelogramului.
Se poate o indicaţie, ceva?
Fie ABCD paralelogram, în planul P, astfel încât AB paralelă cu DC si AD paralelă cu BC.
Fie un punct E, în planul P, astfel încât dreapta EC este perpendiculară pe BC în punctul C şi EA perpendiculară pe AB în punctul A.
Să se demonstreze că dreapta ED este perpendiculară pe diagonala AC a paralelogramului.
Se poate o indicaţie, ceva?
_________________
Eşti inteligent atunci când crezi doar jumătate din ceea ce afli; eşti înţelept atunci când ştii care jumătate!

Razvan- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 6183




Puncte : 33836
Data de inscriere : 18/03/2011
 Re: O problema de geometrie
Re: O problema de geometrie
Punctele E, C si A sunt coliniare, deoarece apartin aceleiasi drepte AE, perpendiculare pe laturile AD si BC, ale paralelogramului, care la randul lor sunt paralele.
Daca EA este perpendiculara pe AD in punctul A, unind E cu D se formeaza triunghiul dreptunghic ADE cu unghiul drept in A, iar dreapta ED nu poate fi perpendiculara pe AC, pentru ca ar insemna ca ED sa fie perpend. pe AE, punctul C fiind coliniar cu A,C,E.
Cred ca daca ai atasa un desen ar fi mai graitor.
Daca EA este perpendiculara pe AD in punctul A, unind E cu D se formeaza triunghiul dreptunghic ADE cu unghiul drept in A, iar dreapta ED nu poate fi perpendiculara pe AC, pentru ca ar insemna ca ED sa fie perpend. pe AE, punctul C fiind coliniar cu A,C,E.
Cred ca daca ai atasa un desen ar fi mai graitor.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12459
Puncte : 56976
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: O problema de geometrie
Re: O problema de geometrie
Confuzia generată este că punctul E nu aparţine planului P, în care se află paralelogramul. De fapt, el se află în acelaşi plan cu paralelogramul (din ipoteză). Figura nu este în spaţiu.
E o problemă care i s-a dat fiicei mele, pe lângă altele, ca recapitulare pentru o testare la matematică. Ei bine, în testul dat la clasă nu s-a mai dat şi această problemă, astfel încât nici profa lor nu le-a mai arătat rezolvarea. În schimb, pe mine mă obsedează! Am încercat cu calculul unghiurilor, să caut triunghiuri asemenea, dar se complică prea mult şi nu iese nimic.
Iată figura:
 https://2img.net/r/ihimizer/i/fig1f.jpg/
https://2img.net/r/ihimizer/i/fig1f.jpg/
E o problemă care i s-a dat fiicei mele, pe lângă altele, ca recapitulare pentru o testare la matematică. Ei bine, în testul dat la clasă nu s-a mai dat şi această problemă, astfel încât nici profa lor nu le-a mai arătat rezolvarea. În schimb, pe mine mă obsedează! Am încercat cu calculul unghiurilor, să caut triunghiuri asemenea, dar se complică prea mult şi nu iese nimic.
Iată figura:
 https://2img.net/r/ihimizer/i/fig1f.jpg/
https://2img.net/r/ihimizer/i/fig1f.jpg/_________________
Eşti inteligent atunci când crezi doar jumătate din ceea ce afli; eşti înţelept atunci când ştii care jumătate!

Razvan- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 6183




Puncte : 33836
Data de inscriere : 18/03/2011
 Re: O problema de geometrie
Re: O problema de geometrie
Nu este clar de loc textul problemei. daca figura este in planul P, atunci triunghiul EAC este drept in punctul A, iar triung.ECB este drept in pct.C Deci figura formata din cele doua triunghiuri este un patrat EABC, asta inseamna ca punctul E se suprapune cu punctul D, iar paralelogramul de fapt este un patrat. In acest caz EB este tot una cu DB ca diagonala a patratului ce va fi perpendiculara pe AC care este cealalta diagonala a patratului. (diagonalele unui patrat sunt perpendiculare).
Paralelogramul din problema este de fapt un patrat.
Paralelogramul din problema este de fapt un patrat.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12459
Puncte : 56976
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: O problema de geometrie
Re: O problema de geometrie
Figura EABC de care zici este un patrulater care are două unghiuri drepte opuse. Cum suma măsurilor unghiurilor unui patrulater este 360o, rezultă de aici că suma măsurilor unghiurilor ABC şi AEC este 180o. Asta nu înseamnă că musai ABC şi AEC să aibe câte 90o. Cu ABCD pătrat, ar fi doar un caz particular şi atunci era simplu. Dar, în ipoteză se specifică în mod clar că e vorba de un paralelogram (nici măcar romb).
_________________
Eşti inteligent atunci când crezi doar jumătate din ceea ce afli; eşti înţelept atunci când ştii care jumătate!

Razvan- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 6183




Puncte : 33836
Data de inscriere : 18/03/2011
 Re: O problema de geometrie
Re: O problema de geometrie
Din textul problemei rezulta ca, trebuie demonstrat ca diagonalele sunt perpendiculare. Asta se poate intampla cand figura respectiva este un patrat sau un romb. Atat patratul cat si rombul sunt cazuri particulare ale unui paralelogram. Alta rezolvare nu cred ca este.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12459
Puncte : 56976
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: O problema de geometrie
Re: O problema de geometrie
Hai că i-am dat până la urmă de capăt! E simplă de tot, numai că trebuie să mai desenezi ceva, ca în figura ataşată.

Demonstraţie:
Avem AB paralelă cu DC (din ipoteză – ABCD fiind paralelogram) şi AD paralelă cu BC.
Dacă prelungim AD, până va intersecta EC, în punctul N, atunci AN va fi perpendiculară pe EC în N (deoarece AN paralelă cu BC care este perpendiculară pe EC – din ipoteză).
Prelungim şi CD până va intersecta EA în punctul M; CM va fi şi ea perpendiculară pe EA în M (deoarece CM paralelă cu AB care este perpendiculară pe AE – din ipoteză).
Aşadar avem triunghiul format EAC, unde AN şi CM sunt înălţimi. Punctul D se află la intersecţia a două înălţimi, deci este ortocentru în triunghiul EAC.
Dreapta ED, trece prin ortocentru, deci este la rândul ei înălţime şi deci perpendiculară pe latura opusă, AC.
Oricum, problema e frumoasă, dar e şi cam încurcătoare. Prima dată mă apucasem să calculez unghiuri şi se complica rău de tot. Pe urmă (după îndelungi transpiraţii) m-am gândit să folosesc faptul că ABCD este paralelogram. Şi aşa i-am dat de capăt. Sper că n-am greşit pe undeva, având în vedere că nu am mai rezolvat probleme de j'de ani!
Mulţumesc mult, Virgil, pentru interesul acordat! Chestia cu pătratul mi-a dat idei să folosesc faptul că ABCD este paralelogram.

Demonstraţie:
Avem AB paralelă cu DC (din ipoteză – ABCD fiind paralelogram) şi AD paralelă cu BC.
Dacă prelungim AD, până va intersecta EC, în punctul N, atunci AN va fi perpendiculară pe EC în N (deoarece AN paralelă cu BC care este perpendiculară pe EC – din ipoteză).
Prelungim şi CD până va intersecta EA în punctul M; CM va fi şi ea perpendiculară pe EA în M (deoarece CM paralelă cu AB care este perpendiculară pe AE – din ipoteză).
Aşadar avem triunghiul format EAC, unde AN şi CM sunt înălţimi. Punctul D se află la intersecţia a două înălţimi, deci este ortocentru în triunghiul EAC.
Dreapta ED, trece prin ortocentru, deci este la rândul ei înălţime şi deci perpendiculară pe latura opusă, AC.
Oricum, problema e frumoasă, dar e şi cam încurcătoare. Prima dată mă apucasem să calculez unghiuri şi se complica rău de tot. Pe urmă (după îndelungi transpiraţii) m-am gândit să folosesc faptul că ABCD este paralelogram. Şi aşa i-am dat de capăt. Sper că n-am greşit pe undeva, având în vedere că nu am mai rezolvat probleme de j'de ani!
Mulţumesc mult, Virgil, pentru interesul acordat! Chestia cu pătratul mi-a dat idei să folosesc faptul că ABCD este paralelogram.
_________________
Eşti inteligent atunci când crezi doar jumătate din ceea ce afli; eşti înţelept atunci când ştii care jumătate!

Razvan- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 6183




Puncte : 33836
Data de inscriere : 18/03/2011
 Re: O problema de geometrie
Re: O problema de geometrie
Bine ca ti-ai gasit linistea.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12459
Puncte : 56976
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: O problema de geometrie
Re: O problema de geometrie
Se poate demonstra că într-un triunghi ascuțitunghic, ca cel de mai jos :

unde h și h' sunt înălțimile pe laturile AB și respectiv BC,
există egalitatea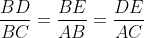
Evident, primele două sunt egale, reprezentând cosinusul unghiului B.
Nu reușesc să demonstrez egalitatea și cu ultimul raport, deși pare să-mi rezulte printr-o implicație...algebrică, să-i spunem.
Asta dacă nu am greșit pe undeva.
Are cineva vreo idee despre cum se poate demonstra dacă este sau nu adevărată egalitatea de mai sus ?

unde h și h' sunt înălțimile pe laturile AB și respectiv BC,
există egalitatea
Evident, primele două sunt egale, reprezentând cosinusul unghiului B.
Nu reușesc să demonstrez egalitatea și cu ultimul raport, deși pare să-mi rezulte printr-o implicație...algebrică, să-i spunem.
Asta dacă nu am greșit pe undeva.
Are cineva vreo idee despre cum se poate demonstra dacă este sau nu adevărată egalitatea de mai sus ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O problema de geometrie
Re: O problema de geometrie
Am încercat, poate insuficient, cine știe...
Oricum, am ajuns la acest rezultat arătând că dacă există un n, și există unul chiar dacă este real, dar nu intru acum în detalii, pentru care^n+(BC)^n=(AC)^n) , atunci rezultă că pentru acel n, în condițiile din triunghiul de mai sus, este adevărat și că
, atunci rezultă că pentru acel n, în condițiile din triunghiul de mai sus, este adevărat și că ^n+(BE)^n=(DE)^n) , dacă este adevărat raportul mai sus menționat.
, dacă este adevărat raportul mai sus menționat.
În fine..., ideea este că geometric, nu am reușit să demonstrez asta și aș fi curios dacă rezultatul obținut în altă parte este corect și verificat geometric, motiv pentru care am deschis întrebarea (problema).
Oricum, am ajuns la acest rezultat arătând că dacă există un n, și există unul chiar dacă este real, dar nu intru acum în detalii, pentru care
În fine..., ideea este că geometric, nu am reușit să demonstrez asta și aș fi curios dacă rezultatul obținut în altă parte este corect și verificat geometric, motiv pentru care am deschis întrebarea (problema).
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O problema de geometrie
Re: O problema de geometrie
curiosul a scris:Se poate demonstra că într-un triunghi ascuțitunghic, ca cel de mai jos :
unde h și h' sunt înălțimile pe laturile AB și respectiv BC,
există egalitatea
Evident, primele două sunt egale, reprezentând cosinusul unghiului B.
Nu reușesc să demonstrez egalitatea și cu ultimul raport, deși pare să-mi rezulte printr-o implicație...algebrică, să-i spunem.
Asta dacă nu am greșit pe undeva.
Are cineva vreo idee despre cum se poate demonstra dacă este sau nu adevărată egalitatea de mai sus ?
Asa la prima vedere eu zic ca nu este corecta a doua egalitate. Egalitatea ar fi corecta daca triunghiul ar fi isoscel.
E multa bataie de cap cu calculele.
Da un exemplu numeric ca este mai simplu,daca da corect merita sa ne batem capul si cu demonstratia analitica.
De exemplu ia laturile 5,6,7.Ca precis este ascutitunghic
Cu Heron gasesti Suprafata
Din suprafata gasesti h si h'
Din h si h' gasesti segmentele ... si asa din aproape in aproape gasesti toate elementele
Faci rapoartele si vezi daca a doua egalitate da corect.
Daca este corecta refacem rationamentul si analitic.Dar inca odata dupa parerea mea slabe sanse.
Vizitator- Vizitator
 Re: O problema de geometrie
Re: O problema de geometrie
Pare să fie adevărată, Orakle.
O să-ți scriu mai târziu cum am gândit, dacă am timp, pentru că într-adevăr, e ceva de scris și n-am timp să redactez în LaTex.
Asta dacă n-am greșit cumva pe undeva.
O să-ți scriu mai târziu cum am gândit, dacă am timp, pentru că într-adevăr, e ceva de scris și n-am timp să redactez în LaTex.
Asta dacă n-am greșit cumva pe undeva.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O problema de geometrie
Re: O problema de geometrie
curiosul a scris:Pare să fie adevărată, Orakle.
O să-ți scriu mai târziu cum am gândit, dacă am timp, pentru că într-adevăr, e ceva de scris și n-am timp să redactez în LaTex.
Asta dacă n-am greșit cumva pe undeva.
Iti fac eu demonstratia ca la carte imediat ce am un pic de timp liber.
Vizitator- Vizitator
 Re: O problema de geometrie
Re: O problema de geometrie
Fie triunghiul ascutitunghic ABC
Pentru a simplifica scrierea renotam:
AB=c
AC=b
BC=a
1-Orice triunghi este unic definit de valorile (abc). Consideram aceste variabile ca fiind variabilele de baza si explicitam restul elementelor in functie de aceste variabile.
2-Din ipoteza triunghiul este ascutitunghic.
Aceasta ipoteza este echivalenta cu conditia ca valoarea unghiurilor A,B,C sa fie intre 0 si 90 de grade,conditie care se poate rescrie ca cosA,cosB,cosC sa fie valori pozitive.
Folosind conditia de mai sus din Teorema lui pitagora generalizata:
a^2=b^2+c^2-2bscosA
rezulta:
b^2+c^2-a^2>0 (1.1)
Efectuand similar calculele si pentru laturile b si c rezulta :
a^2+c^2-b^2>0 (1.2)
a^2+b^2-c^2>0 (1.3)
Cele trei conditii (1.1)-(1.3) sunt conditile necesare pentru ca triunghiul ABC sa fie tr. obtuzunghic.
Pentru a ne verifica calculele vom efectua si un calcul numeric.Calcul in care vom folosi valorile a=5 ,b=6 ,c=7 Valori care verifica conditiile de mai sus.
3.Considerand abc variablele de baza folosind formula lui Heron putem gasi aria triunghiului ABC in functie de aceste variabile.
(p-b)(p-c)})
unde cu p am notat semiperimetrul triunghiului ABC
p=(a+b+c)/2
In cazul exemplului nostru p=9 si S=(9*4*3*2)^0.5=6*6^0.5
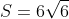
Pentru a simplifica scrierea renotam:
AB=c
AC=b
BC=a
1-Orice triunghi este unic definit de valorile (abc). Consideram aceste variabile ca fiind variabilele de baza si explicitam restul elementelor in functie de aceste variabile.
2-Din ipoteza triunghiul este ascutitunghic.
Aceasta ipoteza este echivalenta cu conditia ca valoarea unghiurilor A,B,C sa fie intre 0 si 90 de grade,conditie care se poate rescrie ca cosA,cosB,cosC sa fie valori pozitive.
Folosind conditia de mai sus din Teorema lui pitagora generalizata:
a^2=b^2+c^2-2bscosA
rezulta:
b^2+c^2-a^2>0 (1.1)
Efectuand similar calculele si pentru laturile b si c rezulta :
a^2+c^2-b^2>0 (1.2)
a^2+b^2-c^2>0 (1.3)
Cele trei conditii (1.1)-(1.3) sunt conditile necesare pentru ca triunghiul ABC sa fie tr. obtuzunghic.
Pentru a ne verifica calculele vom efectua si un calcul numeric.Calcul in care vom folosi valorile a=5 ,b=6 ,c=7 Valori care verifica conditiile de mai sus.
3.Considerand abc variablele de baza folosind formula lui Heron putem gasi aria triunghiului ABC in functie de aceste variabile.
unde cu p am notat semiperimetrul triunghiului ABC
p=(a+b+c)/2
In cazul exemplului nostru p=9 si S=(9*4*3*2)^0.5=6*6^0.5
Vizitator- Vizitator
 Re: O problema de geometrie
Re: O problema de geometrie
Nu Orakle, Abel are dreptate, rezultă prin LUL la asemănare. 
Practic, dacă ai roti triunghiul DBE, aducând D în locul lui E (adică pe BC, că nu cade în același punct cu E) și E în locul lui D (respectiv, adică pe AB) , ED ar fi paralelă cu AC.
Triunghiul nu e desenat corect, dar așa ar trebui să fie.
Practic ai același unghi B, și celelalte două laturi respectând proporționalitatea, ceea ce înseamnă că triunghiurile sunt asemenea și implicit egalitatea menționată inițial se respectă și cu ultimul termen.
E un fel de Thales, dar trebuie privit invers triunghiul din vârf, rotit 180 de grade cu B fixat.
Asta e de bine, îmi confirmă că rezultatul la care am ajuns în cealaltă parte este corect.
O să-ți arăt la ce folosește (în ce am analizat eu, cel puțin), dar într-un alt subiect și mai probabil mâine, că azi nu am timp.
Practic, dacă ai roti triunghiul DBE, aducând D în locul lui E (adică pe BC, că nu cade în același punct cu E) și E în locul lui D (respectiv, adică pe AB) , ED ar fi paralelă cu AC.
Triunghiul nu e desenat corect, dar așa ar trebui să fie.
Practic ai același unghi B, și celelalte două laturi respectând proporționalitatea, ceea ce înseamnă că triunghiurile sunt asemenea și implicit egalitatea menționată inițial se respectă și cu ultimul termen.
E un fel de Thales, dar trebuie privit invers triunghiul din vârf, rotit 180 de grade cu B fixat.
Asta e de bine, îmi confirmă că rezultatul la care am ajuns în cealaltă parte este corect.
O să-ți arăt la ce folosește (în ce am analizat eu, cel puțin), dar într-un alt subiect și mai probabil mâine, că azi nu am timp.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O problema de geometrie
Re: O problema de geometrie
Da! Ai dreptate egalitatea este corecta !
I-am dat de capat !Si este simplu de demonstrat.

I-am dat de capat !Si este simplu de demonstrat.


Vizitator- Vizitator
 Re: O problema de geometrie
Re: O problema de geometrie
In triunghiul mare ABC scriem teorema lui Pitagora generalizata:
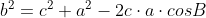
In triunghiul mic DBE scriem teorema lui Pitagora generalizata:

Dar din cele doua triunghiuri dreptunghice rezulta:
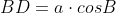
respectiv:
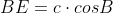
Introducem in T.P. scrisa pentru triunghiul DBE si rezulta:
![DE^2=(c\cdot cosB)^2+(a\cdot cosB)^2-2(c\cdot cosB)(a\cdot cosB)cosB= (cosB)^2\left [ c^2+a^2-2c\cdot a\cdot cosB \right ]](http://latex.codecogs.com/gif.latex?DE^2=(c\cdot&space;cosB)^2+(a\cdot&space;cosB)^2-2(c\cdot&space;cosB)(a\cdot&space;cosB)cosB=&space;(cosB)^2\left&space;[&space;c^2+a^2-2c\cdot&space;a\cdot&space;cosB&space;\right&space;])
paranteza din membrul drept este exact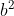 rezulta:
rezulta:
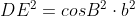
De unde rezulta:
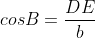 exact egalitatea discutata.
exact egalitatea discutata.
Pentru demonstratia asta nu ai nevoie de valorile lui h si h' asa ca nu are rost sa te complici cu Heron.
E mai simplu asa daca nu ai nevoie si de alte elemente din triunghi.
Demonstratiile pe baza de asemanari nu zic ca nu sunt bune dar pentru siguranta e mai bine sa faci demonstratii folosind calcule analitice
Este urmat de topicul „Alte aspecte privind teorema lui Fermat”.
In triunghiul mic DBE scriem teorema lui Pitagora generalizata:
Dar din cele doua triunghiuri dreptunghice rezulta:
respectiv:
Introducem in T.P. scrisa pentru triunghiul DBE si rezulta:
paranteza din membrul drept este exact
De unde rezulta:
Pentru demonstratia asta nu ai nevoie de valorile lui h si h' asa ca nu are rost sa te complici cu Heron.
E mai simplu asa daca nu ai nevoie si de alte elemente din triunghi.
Demonstratiile pe baza de asemanari nu zic ca nu sunt bune dar pentru siguranta e mai bine sa faci demonstratii folosind calcule analitice
Este urmat de topicul „Alte aspecte privind teorema lui Fermat”.
Ultima editare efectuata de catre Abel Cavaşi in Mar 26 Aug 2014, 20:36, editata de 1 ori (Motiv : Este urmat de topicul...)
Vizitator- Vizitator
 Re: O problema de geometrie
Re: O problema de geometrie
Corect!Triunghiul trebuie să fie un triunghi isoscel cu AB=AC şi nu neapărat ascuţitunghic sau un triunghi echilateral pentru a avea acel şir de trei rapoarte egale.orakle a scris:Asa la prima vedere eu zic ca nu este corecta a doua egalitate. Egalitatea ar fi corecta daca triunghiul ar fi isoscel.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: O problema de geometrie
Re: O problema de geometrie
Dacu a scris:Corect!Triunghiul trebuie să fie un triunghi isoscel cu AB=AC şi nu neapărat ascuţitunghic sau un triunghi echilateral pentru a avea acel şir de trei rapoarte egale.orakle a scris:Asa la prima vedere eu zic ca nu este corecta a doua egalitate. Egalitatea ar fi corecta daca triunghiul ar fi isoscel.
Citește asta :
orakle a scris:In triunghiul mare ABC scriem teorema lui Pitagora generalizata:
In triunghiul mic DBE scriem teorema lui Pitagora generalizata:
Dar din cele doua triunghiuri dreptunghice rezulta:
respectiv:
Introducem in T.P. scrisa pentru triunghiul DBE si rezulta:
paranteza din membrul drept este exactrezulta:
De unde rezulta:exact egalitatea discutata.
Pentru demonstratia asta nu ai nevoie de valorile lui h si h' asa ca nu are rost sa te complici cu Heron.
E mai simplu asa daca nu ai nevoie si de alte elemente din triunghi.
Demonstratiile pe baza de asemanari nu zic ca nu sunt bune dar pentru siguranta e mai bine sa faci demonstratii folosind calcule analitice
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: O problema de geometrie
Re: O problema de geometrie
Repet si corectez (nu am fost atent la notaţiile vârfurilor triunghiului):orakle a scris:Asa la prima vedere eu zic ca nu este corecta a doua egalitate. Egalitatea ar fi corecta daca triunghiul ar fi isoscel.
Triunghiul ABC trebuie să fie isoscel cu AB=BC ascuţitunghic sau obtuzunghic sau isoscel dreptunghic cu unghiul A=90 grade sexagesimale sau trebuie sa fie un triunghi echilateral pentru ca să existe acel sir de trei rapoarte egale.
Mii de scuze!
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: O problema de geometrie
Re: O problema de geometrie
Părerea mea Dacule, este că demonstrația lui Orakle este general valabilă pentru orice triunghi ascuțitunghic. În demonstrația lui Orakle nu apare niciun aspect care să restricționeze situația, fiind valabilă doar pentru triunghiul isoscel, sau pentru genul de triunghiuri pe care le-ai menționat.
Mă înșel ?
Mă înșel ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Subiecte similare
Subiecte similare» [Rezolvat]Problemă cu teoria gravitaţiei? NU. Problema este rezolvată în cazul nerelativist.
» Problemă
» O problema de chimie....
» Problemă
» O problema de chimie....
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 
