Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Meteorr Ieri la 21:34
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Joi 21 Noi 2024, 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la Abel Cavaşi în Daci nemuritori
( 1 )
» Mesaj de la CAdi în Fenomene Electromagnetice
( 1 )
» Mesaj de la virgil în Fiinte deosebite.
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| Dacu2 | ||||
| eugen | ||||
| Forever_Man | ||||
| Abel Cavaşi | ||||
| Meteorr |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| virgil | ||||
| Dacu2 | ||||
| CAdi | ||||
| Meteorr | ||||
| ilasus | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 45 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 45 Vizitatori :: 1 Motor de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Alte aspecte privind teorema lui Fermat
4 participanți
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 2 din 2
Pagina 2 din 2 •  1, 2
1, 2
 Alte aspecte privind teorema lui Fermat
Alte aspecte privind teorema lui Fermat
Rezumarea primului mesaj :
Provine din topicul „O problema de geometrie”.
Da Orakle, frumos demonstrat, felicitări !
Am analizat un pic ce ai scris, am mai citit câte ceva și de prin trigonometrie și am găsit o relație trigonometrică foarte frumoasă care implică Marea teoremă a lui Fermat, relație de implicare ce are de asemenea o demonstrație superbă. Mă refer doar la demonstrația relației de implicare a teoremei, nu a demonstrației teoremei propriu-zise. Nu am timp acum s-o scriu dar o voi face curând pentru că merită și cred că am găsit și niște relații trigonometrice noi între laturile unui triunghi.
Și anume.
Soluțiile x, y, z ale ecuației trebuie să fie întregi pozitive, prime între ele și să fie laturile unui triunghi.
Plecând de la triunghi, relația de implicare este :
Ecuația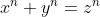 are soluții întregi pozitive, dacă
are soluții întregi pozitive, dacă 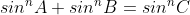 , unde A este unghiul format de x și z, B este unghiul format de y și z, iar C este unghiul format de x și y.
, unde A este unghiul format de x și z, B este unghiul format de y și z, iar C este unghiul format de x și y.
În consecință, putem ajunge la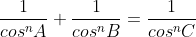 unde putem înlocui valorile cosinusurilor prin valorile determinate de teorema cosinusului și vedem ce rezultă.
unde putem înlocui valorile cosinusurilor prin valorile determinate de teorema cosinusului și vedem ce rezultă.
Nu am mai avut timp aseară să mai continuu, dar cred că o voi face în seara asta și să văd la ce rezultat mai ajung.
Tu ai vreo idee, plecând de aici ?
Voi prezenta și demonstrația relației de implicare.
Este superbă !
Provine din topicul „O problema de geometrie”.
Da Orakle, frumos demonstrat, felicitări !
Am analizat un pic ce ai scris, am mai citit câte ceva și de prin trigonometrie și am găsit o relație trigonometrică foarte frumoasă care implică Marea teoremă a lui Fermat, relație de implicare ce are de asemenea o demonstrație superbă. Mă refer doar la demonstrația relației de implicare a teoremei, nu a demonstrației teoremei propriu-zise. Nu am timp acum s-o scriu dar o voi face curând pentru că merită și cred că am găsit și niște relații trigonometrice noi între laturile unui triunghi.
Și anume.
Soluțiile x, y, z ale ecuației trebuie să fie întregi pozitive, prime între ele și să fie laturile unui triunghi.
Plecând de la triunghi, relația de implicare este :
Ecuația
În consecință, putem ajunge la
Nu am mai avut timp aseară să mai continuu, dar cred că o voi face în seara asta și să văd la ce rezultat mai ajung.
Tu ai vreo idee, plecând de aici ?
Voi prezenta și demonstrația relației de implicare.
Este superbă !
Ultima editare efectuata de catre Abel Cavaşi in Mar 26 Aug 2014, 20:37, editata de 1 ori (Motiv : Provine din topicul...)
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Pacalici a scris:Io zic asahe, Dacii or fost primi care or inventat Teorema lu Fermat si Fermat o fost plagiator.Experienta recenta ne arata ca Romanii, urmashi Dacilor sunt Miezul Pamantului!
Si normal.
Exista si o axioma prin care se sustine asta.Axioma de pe vremea Dacilor.
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Da Dacule, matematică de clasa a treia, nu comentez nimic aici, pentru că mai mult nici nu-mi permite pregătirea pe care o am.
Însă, deși e de clasa a treia, se pare că eu știu să o aplic mai bine ca tine.
Folosind matematica asta de clasa a treia am reușit să arăt că dacă într-un triunghi este adevărat faptul că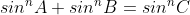 atunci trebuie obligatoriu să fie adevărată și egalitatea
atunci trebuie obligatoriu să fie adevărată și egalitatea ^n) ,
,
bazat în principiu pe faptul că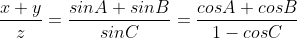
Dar am găsit un raționament și mai simplu, care duce cumva la același rezultat cu acesta de mai sus, dar pentru care ar trebui să scriu ceva mai mult, și care-i este adresat lui Orakle, deoarece nivelul tău superior nu acceptă soluții simple pentru probleme care sunt totuși ceva mai complicate.
Așadar Orakle, spune-mi te rog părerea la mesajul pe care-l voi scrie în continuare. O să încerc să simplific cât pot. Am ajuns la acest rezultat prin mai multe modalități diferite, ceea ce îmi spune că est puțin probabil să fie greșit. Dar oricum, să vedem ce-am mai găsit.
Însă, deși e de clasa a treia, se pare că eu știu să o aplic mai bine ca tine.
Folosind matematica asta de clasa a treia am reușit să arăt că dacă într-un triunghi este adevărat faptul că
bazat în principiu pe faptul că
Dar am găsit un raționament și mai simplu, care duce cumva la același rezultat cu acesta de mai sus, dar pentru care ar trebui să scriu ceva mai mult, și care-i este adresat lui Orakle, deoarece nivelul tău superior nu acceptă soluții simple pentru probleme care sunt totuși ceva mai complicate.
Așadar Orakle, spune-mi te rog părerea la mesajul pe care-l voi scrie în continuare. O să încerc să simplific cât pot. Am ajuns la acest rezultat prin mai multe modalități diferite, ceea ce îmi spune că est puțin probabil să fie greșit. Dar oricum, să vedem ce-am mai găsit.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Numarul mesajelor : 6790
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Păi Orakle, iar vorbim de un raport și nu de o egalitate.
Păi sinA+sinB=cosA+cosB ?
Dar oricum, nu voi folosi asta, deși se poate ajunge și la acest raport.
Mi-a ieșit analizat în mai multe moduri.
Redactez acum varianta mai simplificată.
Păi sinA+sinB=cosA+cosB ?
Dar oricum, nu voi folosi asta, deși se poate ajunge și la acest raport.
Mi-a ieșit analizat în mai multe moduri.
Redactez acum varianta mai simplificată.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Ok.
Intra cat mai mult in detalii sa nu trebuiasca sa le potrivesc eu.Si sa intreb aiurea.
Intra cat mai mult in detalii sa nu trebuiasca sa le potrivesc eu.Si sa intreb aiurea.
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Hai să-ți arăt cum am ajuns la aceea egalitate, prin matematica aia de clasa a treia, deși nu o voi folosi pe aceea, pentru că am găsit o variantă mult mai simplificată.
Oricum, am azi toată ziua la dispoziție și să-ți arăt cât ar trebui scris, numai demonstrând cum se ajunge la această egalitate, trecând peste câțiva mici pași.
Din
se ajunge la
Prin metoda aia ciudată ajungem la și implicit la
și implicit la 
În continuare, folosind teorema cosinusului și egalitatea aia ciudată putem scrie


Analizând ultima parte a egalității (ultimii doi termeni) ajungem la :

\left&space;(&space;1-cosC&space;\right&space;)=z\left&space;(&space;cosA+cosB&space;\right&space;))
de unde rezultă că

De aici mai trebuie dezvoltat încă o căruță de text ca să rezulte că dacă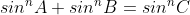 , atunci este adevărat și că
, atunci este adevărat și că ^n) .
.
Dar cum îți spuneam, am ajuns la o variantă simplificată care duce la un rezultat asemănător, dar mult mai simplificat.
În mare, am scris și asta ca să vezi o utilitate a acestei matematici de clasa a treia, deși tu spuneai că este foarte restrictivă.
În mare parte ai dreptate, nu prea o poți folosi pentru numere întregi.
E corect ce-am spus ?
Dacă da, trec mai departe și sper să nu dau de vreo greșeală mică în varianta pe care o consider simplificată, pentru că va trebui să reiau.
Oricum, ca să nu te fac să-ți pierzi timpul degeaba, o să scriu doar ceea ce este corect.
Oricum, am azi toată ziua la dispoziție și să-ți arăt cât ar trebui scris, numai demonstrând cum se ajunge la această egalitate, trecând peste câțiva mici pași.
Din
se ajunge la
Prin metoda aia ciudată ajungem la
În continuare, folosind teorema cosinusului și egalitatea aia ciudată putem scrie
Analizând ultima parte a egalității (ultimii doi termeni) ajungem la :
de unde rezultă că
De aici mai trebuie dezvoltat încă o căruță de text ca să rezulte că dacă
Dar cum îți spuneam, am ajuns la o variantă simplificată care duce la un rezultat asemănător, dar mult mai simplificat.
În mare, am scris și asta ca să vezi o utilitate a acestei matematici de clasa a treia, deși tu spuneai că este foarte restrictivă.
În mare parte ai dreptate, nu prea o poți folosi pentru numere întregi.
E corect ce-am spus ?
Dacă da, trec mai departe și sper să nu dau de vreo greșeală mică în varianta pe care o consider simplificată, pentru că va trebui să reiau.
Oricum, ca să nu te fac să-ți pierzi timpul degeaba, o să scriu doar ceea ce este corect.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
"În continuare, folosind teorema cosinusului și egalitatea aia ciudată putem scrie:...."
La formula asta un pic de explicatii.Pana acolo am prins si pare corect
La formula asta un pic de explicatii.Pana acolo am prins si pare corect
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
orakle a scris:"În continuare, folosind teorema cosinusului și egalitatea aia ciudată putem scrie:...."
La formula asta un pic de explicatii.Pana acolo am prins si pare corect
Îți explic acum.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Prin teorema cosinusului, dacă unghiul C este opus laturii z, unghiul A opus laturi x și unghiul B opus laturii y, avem



Acum să verificăm :


Pare să rezulte exact primul sistem, nu ?
Adică sistemul este corect.
este corect.
În continuare înțelegi ce am făcut ?
Am aplicat exact matematica aia ciudată și simplă.
Acum să verificăm :
Pare să rezulte exact primul sistem, nu ?
Adică sistemul
În continuare înțelegi ce am făcut ?
Am aplicat exact matematica aia ciudată și simplă.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
"Prin teorema cosinusului, dacă unghiul C este opus laturii z, unghiul A opus laturi x și unghiul B opus laturii y, avem"
este gresita dar relatile sunt corecte
A....y
B....x
c....z
Am prins,
nu am verificat sistemul daca este corect dar relatia cu pricina este corecta.
Ridici inaltimile in triunghi si scrii:
Pentru inaltimea ridicata din B :
x=proiectia1 (AD)+proiectia 2(DC)
adica
x=y cosC+zcosA
si asa mai departe
este gresita dar relatile sunt corecte
A....y
B....x
c....z
Am prins,
nu am verificat sistemul daca este corect dar relatia cu pricina este corecta.
Ridici inaltimile in triunghi si scrii:
Pentru inaltimea ridicata din B :
x=proiectia1 (AD)+proiectia 2(DC)
adica
x=y cosC+zcosA
si asa mai departe
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
orakle a scris:"Prin teorema cosinusului, dacă unghiul C este opus laturii z, unghiul A opus laturi x și unghiul B opus laturii y, avem"
este gresita dar relatile sunt corecte
A....y
B....x
c....z
Păi stai un pic, lămurește-mă și cu aspectul acesta, că de multe ori mai fac calcule doar în minte și asociez tot timpul unghiurile cu laturile exact așa cum ți-am spus, iar dacă este greșit aș putea ajunge la relații incorecte.
Este greșit cum am afirmat eu, cum am asociat eu unghiurile cu laturile ?
Ești sigur ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Eu asa zic ca este incorecta fraza.Dar relatiile le ai scrise corect

este teorema sinusului care spune ca rapoartele dintre sinusul unghiului si latura din fata sunt proportionale
http://ro.wikipedia.org/wiki/Teorema_sinusurilor
La teorema cosinusului (Pit.generalizata) unghiul este dintre cele doua laturi pe care le inmultesti in ultima expresie
Cel mai bine este sa retii Teorema cosinusului asa
a^2=b^2+c^2-2bccos(b,c) unghiul b.c sau unghiul fata in fata cu a
b^2=a^2+c^2-2accos(a,c) unghiul a.c sau unghiul fata in fata cu b
respectiv:
c^2=a^2+b^2-2abcos(b,a) unghiul a.b sau unghiul fata in fata cu c
daca careva cos este zero in acel caz reobtii Tr lui Pitagora normala
este teorema sinusului care spune ca rapoartele dintre sinusul unghiului si latura din fata sunt proportionale
http://ro.wikipedia.org/wiki/Teorema_sinusurilor
La teorema cosinusului (Pit.generalizata) unghiul este dintre cele doua laturi pe care le inmultesti in ultima expresie
Cel mai bine este sa retii Teorema cosinusului asa
a^2=b^2+c^2-2bccos(b,c) unghiul b.c sau unghiul fata in fata cu a
b^2=a^2+c^2-2accos(a,c) unghiul a.c sau unghiul fata in fata cu b
respectiv:
c^2=a^2+b^2-2abcos(b,a) unghiul a.b sau unghiul fata in fata cu c
daca careva cos este zero in acel caz reobtii Tr lui Pitagora normala
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Era mai usor de uramrit daca foloseai in loc de x,y,z a,b,c
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Eu, mai primitiv așa, le-am memorat după semn, o dată și după valorile de la numitor.
Spre exemplu, în exprimarea cosinusului, unghiul acelui cosinus este determinat de laturile care apar la numitor și laturile care sunt cu plus la numărător. Dar asta înseamnă că m-am exprimat bine. Nu este greșit cum am spus.
Spre exemplu, dacă C este unghiul format de x și y, atunci pentru exprimarea lui cos C la numărător vom avea x^2+y^2-z^2, iar la numitor vom avea 2xy.
M-am exprimat corect, le-am interpretat corect, pentru ca dacă este unghiul format de x și y, atunci evident, va fi unghiul opus celeilalte laturi, adică unghiul opus laturii Z .
Cu o mică, mică corecție, prin teorema cosinusului, dacă unghiul C este opus laturii z, unghiul A opus laturi y și unghiul B opus laturii x, avem



Spre exemplu, în exprimarea cosinusului, unghiul acelui cosinus este determinat de laturile care apar la numitor și laturile care sunt cu plus la numărător. Dar asta înseamnă că m-am exprimat bine. Nu este greșit cum am spus.
Spre exemplu, dacă C este unghiul format de x și y, atunci pentru exprimarea lui cos C la numărător vom avea x^2+y^2-z^2, iar la numitor vom avea 2xy.
M-am exprimat corect, le-am interpretat corect, pentru ca dacă este unghiul format de x și y, atunci evident, va fi unghiul opus celeilalte laturi, adică unghiul opus laturii Z .
Cu o mică, mică corecție, prin teorema cosinusului, dacă unghiul C este opus laturii z, unghiul A opus laturi y și unghiul B opus laturii x, avem
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Exact asta ziceam si eu
Relatiile erau scrise corect dar exprimarea din fraza respectiva era gresita.
Ai prins idee din postarea mea cu proiectiile alea ?
Relatiile erau scrise corect dar exprimarea din fraza respectiva era gresita.
Ai prins idee din postarea mea cu proiectiile alea ?
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Da, până aici sunt complet de acord cu tine, am analizat un pic dacă diferențele de notații afectează cumva raționamentul ulterior și se pare că nu.
Să trecem la lucrurile mai importante.
Până aici ne-am mai familiarizat puțin cu termenii despre care vom discuta în continuare.
Mai verific o dată și revin cu ceea ce consider că simplifică problema și vom vorbi ulterior.
Până aici mulțumesc pentru micile clarificări.
Să trecem la lucrurile mai importante.
Până aici ne-am mai familiarizat puțin cu termenii despre care vom discuta în continuare.
Mai verific o dată și revin cu ceea ce consider că simplifică problema și vom vorbi ulterior.
Până aici mulțumesc pentru micile clarificări.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Nu afecteaza rationamentul (doamne fereste) dar e mai usor pentru tine si mai usor de urmarit pentru terti
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Măi Orakle, am dat aseară peste o chestie interesantă și m-am oprit de la tot ce analizam și am vrut să scriu în continuare, chestie pe care am analizat-o de aseară continuu și nu găsesc unde apare greșeala.
Evident, ceva este greșit pe undeva, dar nu-mi dau seama unde, deși de aseară o analizez încontinuu.
Analizăm doar certitudinile pe care ne putem baza.
1. Ecuația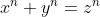 duce indiscutabil la ecuația
duce indiscutabil la ecuația 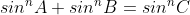
2. Dacă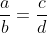 , atunci această egalitate duce la
, atunci această egalitate duce la  , sau, pentru a nu avea probleme de semne, fie analizăm ultimul termen în modul, fie scriem
, sau, pentru a nu avea probleme de semne, fie analizăm ultimul termen în modul, fie scriem  , deși nu asta este important.
, deși nu asta este important.
Acum, prin teorema sinusului avem egalitatea , pe care o putem scrie și la puterea n, adică
, pe care o putem scrie și la puterea n, adică 
Aplicând dezvoltarea prin sumă, de la punctul 2, ajungem la
Dacă aplicăm la ultima egalitate la care s-a ajuns, dezvoltarea prin diferență, tot de la punctul 2, ajungem la

Dar ultimul termen este zero, prin condiția de la punctul 1, ceea ce este imposibil.
Cum explicăm asta ?
Evident, ceva este greșit pe undeva, dar nu-mi dau seama unde, deși de aseară o analizez încontinuu.
Analizăm doar certitudinile pe care ne putem baza.
1. Ecuația
2. Dacă
Acum, prin teorema sinusului avem egalitatea
Aplicând dezvoltarea prin sumă, de la punctul 2, ajungem la
Dacă aplicăm la ultima egalitate la care s-a ajuns, dezvoltarea prin diferență, tot de la punctul 2, ajungem la
Dar ultimul termen este zero, prin condiția de la punctul 1, ceea ce este imposibil.
Cum explicăm asta ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
De fapt e simplu, ce bătut în cap sunt ! 
Mă încurc în lucruri simple de tot.
Acum, că am scris, am văzut unde-i greșeala.a=cși b=d.
Mă încurc în lucruri simple de tot.
Acum, că am scris, am văzut unde-i greșeala.a=cși b=d.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
curiosul a scris:De fapt e simplu, ce bătut în cap sunt !
Mă încurc în lucruri simple de tot.
Acum, că am scris, am văzut unde-i greșeala.a=cși b=d.
Si oricum nu e zero termenul respectiv
e 0/0
Ca sa eviti calculele lungi ulterioare unei gresel foloseste din cand in cand programul
http://www.wolframalpha.com/input/?i=1%3D1
Da valori aiurea la A,B,C (A+B+C=pi) si vezi daca iti confirma daca relatia este adevarata
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Tot de varianta aia mai complicată trebuie să mă folosesc, Orakle.
Mai complicată doar în sensul că e mult de scris.
Mă doare capul numai cât mă gândesc cât am de LaTex-uit.
Cea pe care o credeam simplificată are o greșeală.
Eu o s-o scriu pas cu pas, ca să-ți ușurez cât mai mult munca, iar tu când ai timp citește și analizează.
Oricum, va fi folosită egalitatea
Suntem amândoi de acord că este o egalitate corectă ?
Îți citez din nou mesajul acela :
Mai complicată doar în sensul că e mult de scris.
Mă doare capul numai cât mă gândesc cât am de LaTex-uit.
Cea pe care o credeam simplificată are o greșeală.
Eu o s-o scriu pas cu pas, ca să-ți ușurez cât mai mult munca, iar tu când ai timp citește și analizează.
Oricum, va fi folosită egalitatea
Suntem amândoi de acord că este o egalitate corectă ?
Îți citez din nou mesajul acela :
curiosul a scris:
Din, prin metoda aia ciudată ajungem la
și implicit la
În continuare, folosind teorema cosinusului și egalitatea aia ciudată putem scrie
Analizând ultima parte a egalității (ultimii doi termeni) ajungem la :
de unde rezultă că
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Orakle, dacă tot te consider cenzorul în matematică pe acest forum, am o mică treabă pentru tine.
Te rog să verifici demonstrația trigonometrică a marii teoreme a lui Fermat pe care o voi scrie în altă parte, pentru că o consider corectă.
În principiu este bazată și pe ideile lui Dacu, motiv pentru care îl rog și pe el să-și spună părerea vis-a-vis de această demonstrație.
Vreau asta ca să-mi iau de-o grijă cu teorema asta a lui Fermat și să continuu cu celelalte probleme care mă preocupă.
Deși o să scriu, poate, mai mult decât este necesar, o voi face ca să vă ușurez cât mai mult munca în analiza demonstrației.
Voi redacta în continuare această demonstrație, dar va dura un pic, vreo oră să spunem, până LaTex-uiesc totul.
Oricum, aștept părerea ta, sau a amândurora, sau a oricărui coleg de forum, menționând că se bazează și pe ideile pe care le-a prezentat Dacu pe acest forum, după cum se va vedea.
Eu zic că, în sfârșit, se poate dezvolta pe principii trigonometrice, o demonstrație corectă, indiscutabilă, a teoremei lui Fermat.
Te rog să verifici demonstrația trigonometrică a marii teoreme a lui Fermat pe care o voi scrie în altă parte, pentru că o consider corectă.
În principiu este bazată și pe ideile lui Dacu, motiv pentru care îl rog și pe el să-și spună părerea vis-a-vis de această demonstrație.
Vreau asta ca să-mi iau de-o grijă cu teorema asta a lui Fermat și să continuu cu celelalte probleme care mă preocupă.
Deși o să scriu, poate, mai mult decât este necesar, o voi face ca să vă ușurez cât mai mult munca în analiza demonstrației.
Voi redacta în continuare această demonstrație, dar va dura un pic, vreo oră să spunem, până LaTex-uiesc totul.
Oricum, aștept părerea ta, sau a amândurora, sau a oricărui coleg de forum, menționând că se bazează și pe ideile pe care le-a prezentat Dacu pe acest forum, după cum se va vedea.
Eu zic că, în sfârșit, se poate dezvolta pe principii trigonometrice, o demonstrație corectă, indiscutabilă, a teoremei lui Fermat.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Ok
Dar fi meticulos in demonstratii.Stii ca eu pricep greu si uit repede
Dar fi meticulos in demonstratii.Stii ca eu pricep greu si uit repede
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Promit !
Încerc să-ți ușurez munca în analiză cât mai mult.
Eu zic că-i corectă, să vedem.
Încerc să-ți ușurez munca în analiză cât mai mult.
Eu zic că-i corectă, să vedem.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Numai că s-ar putea să dureze mai mult de o oră, așa cum estimam inițial, ca să fiu atât de meticulos precum o ceri.
Oricum, bănuiesc că nu-i grabă.
Eu, cel puțin, îmi permit să stau mai mult în seara asta ca s-o scriu.
Oricum, bănuiesc că nu-i grabă.
Eu, cel puțin, îmi permit să stau mai mult în seara asta ca s-o scriu.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Nu-i corect Orakle, am găsit o mică greșeală strecurată, care-i demonstrează și lui Dacu că nu este adevărat ceea ce susținea el la un moment dat.
Dacule,
dacă x, y, z sunt laturile unui triunghi, folosind teorema cosinusului, tu erai convins, chiar și eu la un moment dat, că și
și 
Nu poate fi adevărat !
Și avem o problemă destul de consistentă, pentru că ecuația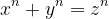 are soluții reale.
are soluții reale.
În primul rând, cu cât cosinusul unui unghi este mai mare, cu atât unghiul este mai mic.
Ecuația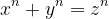 poate fi scrisă
poate fi scrisă ^2+\left&space;(y^{\frac{n}{2}}&space;\right&space;)^2=\left&space;(z^{\frac{n}{2}}&space;\right&space;)^2) , ceea ce înseamnă că dacă ecuația are, algebric, soluții atunci există un triunghi dreptunghic de laturi
, ceea ce înseamnă că dacă ecuația are, algebric, soluții atunci există un triunghi dreptunghic de laturi  ,
,  și
și  , unde cosinusurile unghiurilor a căror sumă este 90 de grade sunt, evident,
, unde cosinusurile unghiurilor a căror sumă este 90 de grade sunt, evident,  și respectiv
și respectiv  .
.
Dacă x, y, z ca și soluții ale ecuației sunt laturile unui triunghi, iar și
și  , atunci înseamnă că cosinusurile acelor unghiuri sunt mai mari decât cele ale triunghiului dreptunghic de laturi
, atunci înseamnă că cosinusurile acelor unghiuri sunt mai mari decât cele ale triunghiului dreptunghic de laturi  ,
,  și
și  .
.
Iar asta înseamnă că dacă cosinusurile unghiurilor triunghiului de laturi x, y, z sunt mai mari ca ale triunghiului dreptunghic, acele unghiuri ale triunghiului de laturi x, y, z sunt mai mici decât ale triunghiului dreptunghic, ceea ce înseamnă că suma acelor două unghiuri ale triunghiului de laturi x, y, z este mai mică de 90 de grade, ceea ce înseamnă că celălalt unghi va fi unul obtuz.
Imposibil !
Pentru că dacă ecuația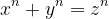 are soluții, ce sunt laturile unui triunghi, se poate demonstra că toate unghiurile trebuie să fie ascuțite.
are soluții, ce sunt laturile unui triunghi, se poate demonstra că toate unghiurile trebuie să fie ascuțite.
Deci undeva avem o problemă !
Sunt două explicații, dar mai întâi vreau să mă asigur că înțelegi ce spun.
Dacule,
dacă x, y, z sunt laturile unui triunghi, folosind teorema cosinusului, tu erai convins, chiar și eu la un moment dat, că
Nu poate fi adevărat !
Și avem o problemă destul de consistentă, pentru că ecuația
În primul rând, cu cât cosinusul unui unghi este mai mare, cu atât unghiul este mai mic.
Ecuația
Dacă x, y, z ca și soluții ale ecuației sunt laturile unui triunghi, iar
Iar asta înseamnă că dacă cosinusurile unghiurilor triunghiului de laturi x, y, z sunt mai mari ca ale triunghiului dreptunghic, acele unghiuri ale triunghiului de laturi x, y, z sunt mai mici decât ale triunghiului dreptunghic, ceea ce înseamnă că suma acelor două unghiuri ale triunghiului de laturi x, y, z este mai mică de 90 de grade, ceea ce înseamnă că celălalt unghi va fi unul obtuz.
Imposibil !
Pentru că dacă ecuația
Deci undeva avem o problemă !
Sunt două explicații, dar mai întâi vreau să mă asigur că înțelegi ce spun.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
O descoperire interesanta legata de numerele prime
http://www.slate.com/articles/health_and_science/do_the_math/2013/05/yitang_zhang_twin_primes_conjecture_a_huge_discovery_about_prime_numbers.html?wpsrc=sh_all_dt_tw_top
Curiosule vezi poate descifrezi ceva.
http://www.slate.com/articles/health_and_science/do_the_math/2013/05/yitang_zhang_twin_primes_conjecture_a_huge_discovery_about_prime_numbers.html?wpsrc=sh_all_dt_tw_top
Curiosule vezi poate descifrezi ceva.
Vizitator- Vizitator
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
orakle a scris:O descoperire interesanta legata de numerele prime
http://www.slate.com/articles/health_and_science/do_the_math/2013/05/yitang_zhang_twin_primes_conjecture_a_huge_discovery_about_prime_numbers.html?wpsrc=sh_all_dt_tw_top
Curiosule vezi poate descifrezi ceva.
Nu spune mare lucru, Orakle.
Chestii comune despre numere și într-un final un pic despre numere prime și cumva despre congruența mod 3.
Dar nimic interesant sau cel puțin ceva care să-mi folosească.
Mai mult, din informațiile pe care le am de pe net, nu s-au mai prea găsit aspecte noi și interesante privind numerele prime.
Din păcate nici eu, deși în ultima perioadă am lucrat ceva mai mult la conjectura lui Goldbach.
Și oricum, deși în documentarul din link se vorbește că distribuția numerelor prime nu este aleatoare, ce-i drept de altfel, nu există și nici nu poate exista vreo formulă de determinare exactă a numerelor prime într-o manieră consecutivă, care să poată fi folosită pentru demonstrarea anumitor ipoteze.
Multe ipoteze privind numerele prime vor rămâne fără demonstrație pentru foarte mult timp de acum încolo.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Plecând de la ideea lui Dacu, adică faptul că soluțiile x, y, z ale ecuației  pot fi considerate laturile unui triunghi deoarece (x+y)>z, (z+x)>y , (z+y)>x, putem stabili alte câteva relații trigonometrice în acel triunghi în raport cu laturi x, y, z.
pot fi considerate laturile unui triunghi deoarece (x+y)>z, (z+x)>y , (z+y)>x, putem stabili alte câteva relații trigonometrice în acel triunghi în raport cu laturi x, y, z.
Dacă , atunci
, atunci  , unde unghiurile A, B și C sunt unghiurile formate de laturile x și z, y și z, respectiv x și y. Să notăm pentru simplificare cu
, unde unghiurile A, B și C sunt unghiurile formate de laturile x și z, y și z, respectiv x și y. Să notăm pentru simplificare cu ,\hat{B}(y,z),\hat{C}(x,y)&space;\right&space;)&space;}) .
.
Dacă , atunci
, atunci ^{n}}+\frac{1}{\left&space;(h_{y}&space;\right&space;)^{n}}=\frac{1}{\left&space;(h_{z}&space;\right&space;)^{n}}&space;}) , unde
, unde  sunt înălțimile pe laturile x, y și respectiv z.
sunt înălțimile pe laturile x, y și respectiv z.
O relație ceva mai interesantă poate fi stabilită cu ajutorul cosinusurilor.
Pentru,\hat{B}(y,z),\hat{C}(x,y)}) , într-un triunghi avem :
, într-un triunghi avem :
+\left&space;(&space;y-z\cdot&space;cos\hat{B}&space;\right&space;)=\left&space;(&space;x+y&space;\right&space;)cos\hat{C}})
iar dacă în triunghiul de laturi x, y, z există relația , atunci avem de asemenea :
, atunci avem de asemenea :
^n+\left&space;(&space;y-z\cdot&space;cos\hat{B}&space;\right&space;)^n=\left&space;(z\cdot&space;cos\hat{C}&space;\right&space;)^n})
Deci am avea două egalități de forma :
+\left&space;(&space;y-&space;{y}'\right&space;)=\left&space;(x+y&space;\right&space;)\cdot&space;{z}'&space;}&space;\\&space;\mathbf{\left&space;(&space;x-{x}'&space;\right&space;)^n+\left&space;(&space;y-&space;{y}'\right&space;)^n=\left&space;(z&space;\right&space;)^n\cdot&space;{z}'^n}&space;\end{cases})
Ce soluții x', y', z' poate avea sistemul ?
Poate avea sistemul de mai sus soluții pentru x' și y' diferite de x'=x(1-z') și y'=y(1-z') ?
Dacă
Dacă
O relație ceva mai interesantă poate fi stabilită cu ajutorul cosinusurilor.
Pentru
iar dacă în triunghiul de laturi x, y, z există relația
Deci am avea două egalități de forma :
Ce soluții x', y', z' poate avea sistemul ?
Poate avea sistemul de mai sus soluții pentru x' și y' diferite de x'=x(1-z') și y'=y(1-z') ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Alte aspecte privind teorema lui Fermat
Re: Alte aspecte privind teorema lui Fermat
Sau, mai general, dacă pentru x, y, z naturale avem egalitățile :
c}&space;\\&space;\mathbf{a^n+b^n=z^nc^n}&space;\end{cases})
ce condiții putem stabili pentru a, b, c naturale ?
Dar raționale pozitive ?
Putem avea alte soluții pentru a și b diferite de a=xc, b=yc ?
ce condiții putem stabili pentru a, b, c naturale ?
Dar raționale pozitive ?
Putem avea alte soluții pentru a și b diferite de a=xc, b=yc ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
Pagina 2 din 2 •  1, 2
1, 2
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 2 din 2
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 