Ultimele subiecte
» În ce tip de dovezi aveţi încredere deplină?Scris de Forever_Man Ieri la 21:41
» Ce anume "generează" legile fizice?
Scris de Forever_Man Ieri la 21:38
» Dovezi ce atestă existența lui DUMNEZEU și că EL este UNICUL CREATOR al Universului
Scris de Forever_Man Ieri la 21:37
» Unde a ajuns stiinta ?
Scris de virgil Ieri la 18:02
» Ce fel de popor suntem
Scris de virgil Ieri la 17:40
» Eu sunt Dumnezeu - viitoarea mea carte in limba romana
Scris de Forever_Man Dum 24 Noi 2024, 09:16
» ChatGPT este din ce în ce mai receptiv
Scris de Meteorr Sam 23 Noi 2024, 21:12
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la CAdi în ChatGPT este din ce în ce mai receptiv
( 1 )
» Mesaj de la CAdi în Ce anume "generează" legile fizice?
( 1 )
» Mesaj de la CAdi în OZN in Romania
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12466) | ||||
| CAdi (12400) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7964) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3970) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Dacu2 | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 19 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 19 Vizitatori :: 2 Motoare de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Pagina 1 din 1
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Empty](https://2img.net/i/empty.gif) Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Ultima editare efectuata de catre meteor in Mier 27 Feb 2013, 21:57, editata de 1 ori
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Empty](https://2img.net/i/empty.gif) Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
-=Introducere=-
Ce importanta are in geometrie, si in restul matematicii fara geometrie, in fizica, etc. teorema lui Pitagora ?!
Ok, raspunsul e clar si a sa imi tiue urechile cind am sa va aud in cor spunind.
Eu altceva vreau sa spun, ca, cine poate rezolva problema de mai sus, acela poate rezolva oorriiccee problema pe care voi le rezolvati cu ajutorul teoremei lui Pitagora(fara a apela la aceasta teorema) + inca o infinitate de alte probleme pe care voi cei ce cunoasteti teorema lui Pitagora nu le veti putea rezolva.
Acest studiu cica ar face parte din capitolul- trigonometrie, eu cred ca e mai ceva, adica apar alte legaturi.
Aproape toata trigonometria, acele formule a unghiurilor: dublu, suma, etc. toate ar cadea, ca ar deveni inutile.
Triunghiul in geometrie, dar si nu numai, este "atomul". Daca am putea diviza la asa dimensiuni si cunoaste perfect de bine structura lui, atunci noi stim si despre restul intreg care e format din acesti "atomi".
De ce triunghiul dreptunghic?!
Deoarece el e componenta principala a "atomului", orice alt triunghi e compus din triunghiuri dreptunghice, orice figura regulata/neregulata e compusa din triunghiuri.
Problema de mai sus mai face "legatura" cu cercul, din care deriva aproape totul.
Adesea asa suna intrebarea:
-Stiinduse valorile unui unghi si a doua laturi se poate de determinat valoarea celeilalte laturi (teorema lui Pitagora)
-Stiinduse valorile a doua unghiuri si o latora se poate de determinat: celelalte doua laturi si celalalt unghi.
Teorema lui Pitagora se include in problema mileniilor, deoarece: cu ajutorul functiilor trigonometrice inverse (arcsin,arcos,..) din cele doua laturi care se dau putem determina cealalta latura si celelalte doua unghiuri.
La fel, va ajuta la calculul functiilor trigonometrice inverse care au o importanta mare.
Despre importanta in restul matematicii si restul fizicii, nu mai vorbesc.
Da, in ziua de azi s-au ajuns la rezultate mari, adica s-a gasit o cale prin care rezultatul este scris sub forma de serie.
Aici e problema, ca nu este comod a se lucra cu aceasta serie (in general cu seriile). Se doreste calculul valorii acestei serii, orice nu ar contine valoarea totala, fie si numere transcendente, orice.
Cine va calcula valoarea sumei seriei, aceala va calcula problema mileniilor, si merita mari aprecieri.
Insa, voi incerca, doar voi incerca nimic in rest, sa incep a rezolva problema pe alte drumuri.
Ce importanta are in geometrie, si in restul matematicii fara geometrie, in fizica, etc. teorema lui Pitagora ?!
Ok, raspunsul e clar si a sa imi tiue urechile cind am sa va aud in cor spunind.
Eu altceva vreau sa spun, ca, cine poate rezolva problema de mai sus, acela poate rezolva oorriiccee problema pe care voi le rezolvati cu ajutorul teoremei lui Pitagora(fara a apela la aceasta teorema) + inca o infinitate de alte probleme pe care voi cei ce cunoasteti teorema lui Pitagora nu le veti putea rezolva.
Acest studiu cica ar face parte din capitolul- trigonometrie, eu cred ca e mai ceva, adica apar alte legaturi.
Aproape toata trigonometria, acele formule a unghiurilor: dublu, suma, etc. toate ar cadea, ca ar deveni inutile.
Triunghiul in geometrie, dar si nu numai, este "atomul". Daca am putea diviza la asa dimensiuni si cunoaste perfect de bine structura lui, atunci noi stim si despre restul intreg care e format din acesti "atomi".
De ce triunghiul dreptunghic?!
Deoarece el e componenta principala a "atomului", orice alt triunghi e compus din triunghiuri dreptunghice, orice figura regulata/neregulata e compusa din triunghiuri.
Problema de mai sus mai face "legatura" cu cercul, din care deriva aproape totul.
Adesea asa suna intrebarea:
-Stiinduse valorile unui unghi si a doua laturi se poate de determinat valoarea celeilalte laturi (teorema lui Pitagora)
-Stiinduse valorile a doua unghiuri si o latora se poate de determinat: celelalte doua laturi si celalalt unghi.
Teorema lui Pitagora se include in problema mileniilor, deoarece: cu ajutorul functiilor trigonometrice inverse (arcsin,arcos,..) din cele doua laturi care se dau putem determina cealalta latura si celelalte doua unghiuri.
La fel, va ajuta la calculul functiilor trigonometrice inverse care au o importanta mare.
Despre importanta in restul matematicii si restul fizicii, nu mai vorbesc.
Da, in ziua de azi s-au ajuns la rezultate mari, adica s-a gasit o cale prin care rezultatul este scris sub forma de serie.
Aici e problema, ca nu este comod a se lucra cu aceasta serie (in general cu seriile). Se doreste calculul valorii acestei serii, orice nu ar contine valoarea totala, fie si numere transcendente, orice.
Cine va calcula valoarea sumei seriei, aceala va calcula problema mileniilor, si merita mari aprecieri.
Insa, voi incerca, doar voi incerca nimic in rest, sa incep a rezolva problema pe alte drumuri.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Empty](https://2img.net/i/empty.gif) Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Conform istoriei spuse din ziua de azi, furat din wikipedia:
INSA, fiti foarte atenti ce se spune in ultima propozitie: " Teorema este valabilă doar în geometria euclidiană, de aceea orice demonstrație foloseste (uneori indirect sau mai puțin vizibil) axioma lui Euclid. "
Cu parere de rau nu am vazut nimic sa se fi spus ceva despre Teorema lui Thales (despre asemanarea triunghiurilor).
Pare ca va spun o abureala, insa teorema(axioma) lui Thales este si ea importanta teorema din geometrie [daca nu am sti nimic de axioma lui Euclid, trebue sa stim ca dupa importanta teorema (axioma) lui Thales este cea mai importanta].
Fara teorema lui Thales, teorema lui Pitagora si problema mileniilor este un nimic.
Dupa cum stiti eu sunt de ideologia ca nici o demonstratie nu e pina la capat facut-a (adica toate coboara pina la axiome), darimite demonstratiile fundamentale ca teorema(axioma) lui Thales - http://ro.wikipedia.org/wiki/Teorema_lui_Thales
Nu prea inteleg din care cauza nu se spune ca exista o legatura strinsa intre axioma lui Thales si teorema lui Pitagora.
Deci trebue de stiut (inclusiv) ca fara omotetie [cred ca omotetia e prezenta peste tot {adica la toategeometriile} doar ca trebue bine batuta la cap, ce si cum e traba acolo cu omotetia..] nu are nici un sens teorema lui Pitagora si problema mileniilor.
Redetaliez.. aceasta din cauza ca aceste teoreme arata ca daca ai un "model" si ai un coeficient de proportionalitate prin modelare determini necunoscutele care doresti sa le afli din problema.
Dupa ce ati citit povestea, cine nu a stiut-o sau a uitat-o, nu cred ca e rau o asa recapitulare.Wikipedia a scris:
Deși teorema se atribuie astăzi filozofului și matematicianului grec antic Pitagora, care a trăit în secolul al șaselea, îdC, se știe cu siguranță că a fost cunoscută de mai toate civilizațiile Pământului de-a lungul timpului: indienii antici, asiro-babilonieni, egiptenii antici, chinezii antici și alții.[1] Subiectul acesta poate fi împărțit în trei: cunoașterea tripletelor pitagoreice (seturi de câte trei numere întregi care reprezintă lungimile laturilor unui triunghi dreptunghic), cunoașterea teoremei propriu-zise, și cunoașterea unei demonstrații.
Tripletele pitagoreice sunt cunoscute de foarte mult timp, ele fiind folosite pentru construirea unui unghi drept în condiții practice: o sfoară este marcată cu noduri aflate la anumite distanțe; formând din ea un triunghi (de exemplu de laturi 3, 4 și 5), acel triunghi va fi dreptunghic - metoda poate fi folosită de exemplu pentru a monta vertical catargul unui vas pe mare.
Monumente megalitice de acum 6000 de ani (în Egipt) sau 4500 de ani (în Insulele Britanice) conțin triunghiuri dreptunghice cu laturi de lungimi numere întregi[2], dar aceasta nu înseamnă neapărat că cei care le-au construit cunoșteau teorema. De asemenea, scrieri vechi din Regatul Mijlociu Egiptean și din Mesopotamia menționează triplete pitagoreice.
Sulba Sutra lui Baudhayana, scrisă în secolul 8 î.e.n. în India, conține o listă de triplete pitagoreice descoperite algebric, un enunț al teoremei, precum și o demonstrație pentru un triunghi dreptunghic isoscel.
Sulba Sutra lui Apastamba (circa 600 î.e.n.) conține o demonstrație numerică a cazului general, calculând arii. Unii cercetători susțin că de aici s-ar fi putut inspira Pitagora, în timpul călătoriei sale în India.
Pitagora (aproximativ 569 - 475 î.e.n.) a folosit metode algebrice pentru a construi triplete pitagoreice, conform lui Proclus. Acesta a scris însă între anii 410 și 485 e.n., adică 9 secole mai târziu. După Sir Thomas L. Heath, teorema nu i-a fost atribuită lui Pitagora timp de cinci secole după perioada în care acesta a trăit. Totuși, atunci când autori cum ar fi Plutarh și Cicero au vorbit despre teoremă ca fiind „a lui Pitagora”, au făcut-o ca și cum acesta era un lucru binecunoscut și de necontestat.
În jurul anului 400 î.e.n., conform lui Proclus, Platon a dat o metodă de a determina triplete pitagoreice care combina algebra și geometria.Există o infinitate de astfel de triplete,forma lor generală fiind x=2uv,y=u2-v2, z=u2+v2,unde u și v sunt numere naturale oarecare,cu u>v. După aproximativ 100 de ani, Euclid a dat în cadrul lucrării Elemente prima demonstrație axiomatică a teoremei.
Scris între 500 î.e.n. și 200 e.n., textul chinezesc Chou Pei Suan Ching (周髀算经) conține o demonstrație vizuală a teoremei.
De fapt, nu numai că nu se poate ști cine a descoperit teorema, dar cercetătorii nu se pot pune de acord nici în privința întrebării dacă a fost descoperită o singură dată, ori independent în istorie de către mai multe civilizații.
Teorema este valabilă doar în geometria euclidiană, de aceea orice demonstrație foloseste (uneori indirect sau mai puțin vizibil) axioma lui Euclid.
INSA, fiti foarte atenti ce se spune in ultima propozitie: " Teorema este valabilă doar în geometria euclidiană, de aceea orice demonstrație foloseste (uneori indirect sau mai puțin vizibil) axioma lui Euclid. "
Cu parere de rau nu am vazut nimic sa se fi spus ceva despre Teorema lui Thales (despre asemanarea triunghiurilor).
Pare ca va spun o abureala, insa teorema(axioma) lui Thales este si ea importanta teorema din geometrie [daca nu am sti nimic de axioma lui Euclid, trebue sa stim ca dupa importanta teorema (axioma) lui Thales este cea mai importanta].
Fara teorema lui Thales, teorema lui Pitagora si problema mileniilor este un nimic.
Dupa cum stiti eu sunt de ideologia ca nici o demonstratie nu e pina la capat facut-a (adica toate coboara pina la axiome), darimite demonstratiile fundamentale ca teorema(axioma) lui Thales - http://ro.wikipedia.org/wiki/Teorema_lui_Thales
Nu prea inteleg din care cauza nu se spune ca exista o legatura strinsa intre axioma lui Thales si teorema lui Pitagora.
Deci trebue de stiut (inclusiv) ca fara omotetie [cred ca omotetia e prezenta peste tot {adica la toategeometriile} doar ca trebue bine batuta la cap, ce si cum e traba acolo cu omotetia..] nu are nici un sens teorema lui Pitagora si problema mileniilor.
Redetaliez.. aceasta din cauza ca aceste teoreme arata ca daca ai un "model" si ai un coeficient de proportionalitate prin modelare determini necunoscutele care doresti sa le afli din problema.
Ultima editare efectuata de catre meteor in Sam 16 Feb 2013, 17:23, editata de 1 ori (Motiv : am reparat ceva exprimari)
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Empty](https://2img.net/i/empty.gif) Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
-=Cuprins=-
Voi mai reveni la Introducere daca vor aparea ceva informatii importante, doar prin editare, nu vreau sa fac subiectul insirat si haustic.
Nus' ce sa fac, deoarece rezolvarea (doar incerc) sa o atac prin 3 cararuse diferite. A scrie prima, apoi a doua, apoi cite un mesaj la prima si apoi la adoua cale deja inseamna un haos, deaceea presupun ca e mai bine sa se "rupa" pe bucatele, macar prin subtitluri.
Voi mai reveni la Introducere daca vor aparea ceva informatii importante, doar prin editare, nu vreau sa fac subiectul insirat si haustic.
Nus' ce sa fac, deoarece rezolvarea (doar incerc) sa o atac prin 3 cararuse diferite. A scrie prima, apoi a doua, apoi cite un mesaj la prima si apoi la adoua cale deja inseamna un haos, deaceea presupun ca e mai bine sa se "rupa" pe bucatele, macar prin subtitluri.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Empty](https://2img.net/i/empty.gif) I. Aplicarea seriilor Taylor
I. Aplicarea seriilor Taylor
Sau poate mai corect spus Maclaurin.
Daca vom calcula o functie trigonometrica, fie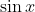 , atunci vom putea determina practic pe toate restul (am in vedere inclusiv si de cele inverse).
, atunci vom putea determina practic pe toate restul (am in vedere inclusiv si de cele inverse).
Avem deci:
^{i}\cdot x^{2i+1}}{(2i+1)!})
Cine calculeaza aceasta valoarea acestei serii aceala rezolva problema.
Pornind de la aceasta conjectura https://cercetare.forumgratuit.ro/t923-factorialul#26548, si "rupind" deoparte sumele negative de cele pozitive, vom avea:
^{4i+1}- \left ( \sum_{j=0}^{4i+3}C_{4i+3}^{2j+1}(4i-2j+5)^{4i+3}\right ) }- \left ( \sum_{i=0}^{\infty } \frac{x^{4i+3}}{\sum_{j=0}^{4i+3}C_{4i+3}^{2j}(4i-2j+5)^{4i+3}-\left ( \sum_{j=0}^{4i+3}C_{4i+3}^{2j+1}(4i-2j+4)^{4i+3} \right )} \right ))
Daca pe cineva l-a ajutat asemenea scriere cu ceva e bine sa ne destainue.
In aceasta scriere problema ramine in combinari, ar fi bine daca am gasi o alta modalitate de a le exprima [a le exprima iarasi prin factorial nu are sens, insa combinarile se pot "descompune" in alte sume de combinari la care bazele sunt diferite], si in sfirsit a calcula intreaga diochenie.
De remarcat, caci in acest caz am determina momentan [se poate si asa prin functia Gama, dar nu vreau ca e si ea strasnica] de determinat aproximativ din o lovitura valoarea lui sinus de x [aplicind integrala] , insa, cine stimeaza matematica e o tilharie si rusine sa lucreze cu aproximatii.
Daca vom calcula o functie trigonometrica, fie
Avem deci:
Cine calculeaza aceasta valoarea acestei serii aceala rezolva problema.
Pornind de la aceasta conjectura https://cercetare.forumgratuit.ro/t923-factorialul#26548, si "rupind" deoparte sumele negative de cele pozitive, vom avea:
Daca pe cineva l-a ajutat asemenea scriere cu ceva e bine sa ne destainue.
In aceasta scriere problema ramine in combinari, ar fi bine daca am gasi o alta modalitate de a le exprima [a le exprima iarasi prin factorial nu are sens, insa combinarile se pot "descompune" in alte sume de combinari la care bazele sunt diferite], si in sfirsit a calcula intreaga diochenie.
De remarcat, caci in acest caz am determina momentan [se poate si asa prin functia Gama, dar nu vreau ca e si ea strasnica] de determinat aproximativ din o lovitura valoarea lui sinus de x [aplicind integrala] , insa, cine stimeaza matematica e o tilharie si rusine sa lucreze cu aproximatii.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Empty](https://2img.net/i/empty.gif) Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Haz de necaz...
Raspuns problema aceasta splendida are, CULMEA, raspunsul e dat deja [din mers] de oameni sfinti de citeva sute de ani in urma.
breeei brei brei..
Are solutia la fel de splendida, presupun insa ca putini[ma tem ca nimeni] nu o pot aprofunda.
Mda.. "cercetator"... zeci de ori am trecut eu (cred ca si voi totii) cu vederea, insa ioc.
Numerele astea complexe is d racul adevarat.
Atit cit is de neplacute atit si misterioase.
Multe minuni au sa ne mai faca ele.
Raspuns problema aceasta splendida are, CULMEA, raspunsul e dat deja [din mers] de oameni sfinti de citeva sute de ani in urma.
breeei brei brei..
Are solutia la fel de splendida, presupun insa ca putini[ma tem ca nimeni] nu o pot aprofunda.
Mda.. "cercetator"... zeci de ori am trecut eu (cred ca si voi totii) cu vederea, insa ioc.
Numerele astea complexe is d racul adevarat.
Atit cit is de neplacute atit si misterioase.
Multe minuni au sa ne mai faca ele.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Empty](https://2img.net/i/empty.gif) Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Faimoasa problema este rezolvata de mult timp in urma.
CULMEA este ca are o rezolvare simpla de vreo chiteva propozitii.
Nu pot sa inteleg din care cauza maretul L. Euler nimic nu a comentat.
[Un alt mister frumos este ca, inainte de Euler, barocul ne-a lasat o piesa la fel de extraordinara:
"Formula lui Euler a fost demonstrată pentru prima dată de Roger Cotes în 1714 sub forma:
=ix) "
"
Eu nu inteleg cum Roger Cotes a put fi sa scrie aceasta piesa extraordinara, daca ea contine elemente, care noi in ziua de ai stim ca ele au fost definite deci si atribuite lui Euler?!
Constanta , unitatea imaginara
, unitatea imaginara  ]
]
Intii de toate a lucrat Taylor, apoi MacLaurin la elaborarea unor serii.
Apoi maretul L.Euler avind aceste rezultate, tot el avind de catre tot el deja dezvoltat suficient studiul cu numerele complexe, si de catre tot el definita mai bine mareata constanta .
.
Iata care e rezolvarea, 0:100 in defavoarea mea..
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Etoix](https://2img.net/r/ihimizer/img842/4419/etoix.png)
sau
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Eix](https://2img.net/r/ihimizer/img836/3304/eix.png)
Si avutia:
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Gsed000100290img9051](https://2img.net/r/ihimizer/img688/9397/gsed000100290img9051.png)
Este ffoarte mult de vorbit despre formula lui Euler, si noile exprimari ale functiilor trigonometrice.
E splendida si are aplicatii infinite.
Am auzit ca si functiile trigonometrice hiperbolice [care joaca ceva roluri in alte geometrii] de aici pornesc de la o simpla inlocuire a lui x cu ix.
In fizica are aplicatii, si aplicatii, cum era lesne de prezis, e si normal.
E fantastica, contine mareata constanta a lui Euler, unitatea imaginara tot de Euler conceputa, este extrem de compacta.
E miraculos cum partea imaginarea in anumite relatii da doar valori reale (pe [-1;1]).
CULMEA este ca are o rezolvare simpla de vreo chiteva propozitii.
Nu pot sa inteleg din care cauza maretul L. Euler nimic nu a comentat.
[Un alt mister frumos este ca, inainte de Euler, barocul ne-a lasat o piesa la fel de extraordinara:
"Formula lui Euler a fost demonstrată pentru prima dată de Roger Cotes în 1714 sub forma:
Eu nu inteleg cum Roger Cotes a put fi sa scrie aceasta piesa extraordinara, daca ea contine elemente, care noi in ziua de ai stim ca ele au fost definite deci si atribuite lui Euler?!
Constanta
Intii de toate a lucrat Taylor, apoi MacLaurin la elaborarea unor serii.
Apoi maretul L.Euler avind aceste rezultate, tot el avind de catre tot el deja dezvoltat suficient studiul cu numerele complexe, si de catre tot el definita mai bine mareata constanta
Iata care e rezolvarea, 0:100 in defavoarea mea..
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Etoix](https://2img.net/r/ihimizer/img842/4419/etoix.png)
sau
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Eix](https://2img.net/r/ihimizer/img836/3304/eix.png)
Si avutia:
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Gsed000100290img9051](https://2img.net/r/ihimizer/img688/9397/gsed000100290img9051.png)
Este ffoarte mult de vorbit despre formula lui Euler, si noile exprimari ale functiilor trigonometrice.
E splendida si are aplicatii infinite.
Am auzit ca si functiile trigonometrice hiperbolice [care joaca ceva roluri in alte geometrii] de aici pornesc de la o simpla inlocuire a lui x cu ix.
In fizica are aplicatii, si aplicatii, cum era lesne de prezis, e si normal.
E fantastica, contine mareata constanta a lui Euler, unitatea imaginara tot de Euler conceputa, este extrem de compacta.
E miraculos cum partea imaginarea in anumite relatii da doar valori reale (pe [-1;1]).
Ultima editare efectuata de catre meteor in Joi 28 Feb 2013, 22:11, editata de 2 ori
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Empty](https://2img.net/i/empty.gif) Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Da si cel mai important am uitat sa va indic, ceea ce trebuia de la inceput, cum rasuna faimoasele rezultate obtinute de sfinti (Taylor, MacLaurin si, in special Euler):
https://www.youtube.com/watch?v=4BDzbKqjW7o
https://www.youtube.com/watch?v=4BDzbKqjW7o
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Empty](https://2img.net/i/empty.gif) Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Aplicind teorema lui Pitagora:
Neaplicind teorema lui Pitagora:
*Acum cred ca problema ramine in unitatea imaginara, cred ca acum omul inca nu e capabil sa il perceapa perfect de bine (macar mediocru) astfel incit sa poata lucra cu asa rezultat compact si formidabil.
Aceasta exprimare a lui
Nu ne-am invatat inca sa putem veadea partea imaginara.
Poateca sa incercam a explica prin exprimarea functiei trigonometrice in modul [stiind un anumit minim interval se poate afla pentru restul], sau cea mai plauzibila idee (care am auzit-o mai demult) cred ca e a incerca sa lucram cu numerele complexe ca fiind matrici bidimensionale, si sa aprofundam studiile in aceasta teorie.
Ultima editare efectuata de catre meteor in Mar 26 Feb 2013, 21:02, editata de 1 ori
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Empty](https://2img.net/i/empty.gif) Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Trebue de retinut faimoasa formula:
+i\sin (x))
Ca importanta in intreaga stiinta eu o consider mult mai importanta ca teorema lui Pitagora, adica ceea ce poate face teorema lui Pitagora, aceasta o face ba si mult mai mult.
Problema cred ca ramine in incapacitatea noastra la moment sa prelucram mai bine numerele complexe, care sunt un mare si frumos mister.
Daca sa aruncam o privire in viitor, am putea doar presupune.
Matematica e infinita in mistere si frumusete, in aplicatii si fascinatii.
Mai departe.. apar alte numere si mai ciudate si faimoase, sa spunem hipercomplexele, care le cuprind pe cele complexe, si care la fel presupun ca ar avea fascinanta lor proprie.
Si apoi ar mai fi si alte numere care ar cuprinde pe cele hipercomplexe si asa mai departe, si cine stie ce minuni mai sunt.
Ca importanta in intreaga stiinta eu o consider mult mai importanta ca teorema lui Pitagora, adica ceea ce poate face teorema lui Pitagora, aceasta o face ba si mult mai mult.
Problema cred ca ramine in incapacitatea noastra la moment sa prelucram mai bine numerele complexe, care sunt un mare si frumos mister.
Daca sa aruncam o privire in viitor, am putea doar presupune.
Matematica e infinita in mistere si frumusete, in aplicatii si fascinatii.
Mai departe.. apar alte numere si mai ciudate si faimoase, sa spunem hipercomplexele, care le cuprind pe cele complexe, si care la fel presupun ca ar avea fascinanta lor proprie.
Si apoi ar mai fi si alte numere care ar cuprinde pe cele hipercomplexe si asa mai departe, si cine stie ce minuni mai sunt.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Empty](https://2img.net/i/empty.gif) Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
--==Rezumat==--
In G.E., cred ca triunghiul este un "atom" important al G.E.
Triunghiul dreptunghic e "mama" acestui "atom".
Ipotetic, eu cred ca, triunghiul dreptunghic este indivizibil.
In G.E. un triunghi este definit complet daca se prezinta un minim de date din cele 3 variante posibile:
1. LUL
2. ULU
3. LLL
Scopul meu este, ca cunoscind acest minim de date, sa le aflam pe restul [ceea ce cred ca e posibil].
Adica, spre exemplu, stii lungimile a doua laturi su un unghi, poftim determinane care este a treea latura si care sunt celelalte doua unghiuri.
1. Primul punct este aproape totalment rezolvat de asa numita teorema a lui Pitagora, care spune caci cunoscind valorile a doua laturi si un unghi in un triunghi [dreptunghic, insa s-a generalizat si este formula si pentru oarecare triunghi] se poate de determinat cealalta latura.
Celelalte unghiuri se pot determina aproximativ din functiile trigonometrice inverse {acest subpunct are strinse legaturi cu punctul 3. altfel spus, cine rezolva acest subpunct acela si rezolva punctul 3. complet}.
Buba e ca eu nu sufar si nu accept aproximarile, deci, cred ca acest subpunct al punctului 1. ramine nerezolvat.
2. ULU. Mi se pare cel mai frumos punct.
Stiinduse lungimile a 2 unghiuri si o latura sa se afle celalt unghi si celelalte 2 laturi.
Euclid, se pare, a gasit o teorema care spune ca in un oarecare triunghi masura unghiurilor este fix 180*.
Deci, celalalt unghi este 180-U1+U2.
Problema: Cum sa aflam celelalte laturi?!
E deajuns sa aflam o latura, caci mai departe aplicam teorema lui Pitagora si poftim ajungem la solutie.
Cum sa o aflam?!
O varianta este: https://cercetare.forumgratuit.ro/t940-problema-mileniilor-una-din-cele-mai-importante-probleme-din-stiinta#27299
Problema e ca pare cam ciudata pentru noi asa o formula compacta si frumoasa, deaceea voi mai incerca putin sa dezvolt subiectul cu alte cararuse incepute mai demult.
Dacu https://cercetare.forumgratuit.ro/t955-problema-mileniilor-in-viziunea-lui-meteor#27375 a propus sa aplicam identitatea lui Euler, cred insa ca aceasta e doar inceputul de drum, mai este de lucru pina cind acele formule frumoase vor fi usor de priceput mie si altora ca mine.
3. Problema consta in a determina masurile unghiurilor triunghiului stiinduse lungimile tuturor laturilor lui.
In ziua de azi, cred ca, aplicind [cel putin] rezultatele lui Taylor-MacLaurin aproximativ se poate de determinat, sau io' stiu sa gasim sau sa facem o analogie cum a facut maretul Euler in calculele sale simple si frumoase.
Calculul aproximativ in sfinta matematica eu cred ca este de neacceptat.
In G.E., cred ca triunghiul este un "atom" important al G.E.
Triunghiul dreptunghic e "mama" acestui "atom".
Ipotetic, eu cred ca, triunghiul dreptunghic este indivizibil.
In G.E. un triunghi este definit complet daca se prezinta un minim de date din cele 3 variante posibile:
1. LUL
2. ULU
3. LLL
Scopul meu este, ca cunoscind acest minim de date, sa le aflam pe restul [ceea ce cred ca e posibil].
Adica, spre exemplu, stii lungimile a doua laturi su un unghi, poftim determinane care este a treea latura si care sunt celelalte doua unghiuri.
1. Primul punct este aproape totalment rezolvat de asa numita teorema a lui Pitagora, care spune caci cunoscind valorile a doua laturi si un unghi in un triunghi [dreptunghic, insa s-a generalizat si este formula si pentru oarecare triunghi] se poate de determinat cealalta latura.
Celelalte unghiuri se pot determina aproximativ din functiile trigonometrice inverse {acest subpunct are strinse legaturi cu punctul 3. altfel spus, cine rezolva acest subpunct acela si rezolva punctul 3. complet}.
Buba e ca eu nu sufar si nu accept aproximarile, deci, cred ca acest subpunct al punctului 1. ramine nerezolvat.
2. ULU. Mi se pare cel mai frumos punct.
Stiinduse lungimile a 2 unghiuri si o latura sa se afle celalt unghi si celelalte 2 laturi.
Euclid, se pare, a gasit o teorema care spune ca in un oarecare triunghi masura unghiurilor este fix 180*.
Deci, celalalt unghi este 180-U1+U2.
Problema: Cum sa aflam celelalte laturi?!
E deajuns sa aflam o latura, caci mai departe aplicam teorema lui Pitagora si poftim ajungem la solutie.
Cum sa o aflam?!
O varianta este: https://cercetare.forumgratuit.ro/t940-problema-mileniilor-una-din-cele-mai-importante-probleme-din-stiinta#27299
Problema e ca pare cam ciudata pentru noi asa o formula compacta si frumoasa, deaceea voi mai incerca putin sa dezvolt subiectul cu alte cararuse incepute mai demult.
Dacu https://cercetare.forumgratuit.ro/t955-problema-mileniilor-in-viziunea-lui-meteor#27375 a propus sa aplicam identitatea lui Euler, cred insa ca aceasta e doar inceputul de drum, mai este de lucru pina cind acele formule frumoase vor fi usor de priceput mie si altora ca mine.
3. Problema consta in a determina masurile unghiurilor triunghiului stiinduse lungimile tuturor laturilor lui.
In ziua de azi, cred ca, aplicind [cel putin] rezultatele lui Taylor-MacLaurin aproximativ se poate de determinat, sau io' stiu sa gasim sau sa facem o analogie cum a facut maretul Euler in calculele sale simple si frumoase.
Calculul aproximativ in sfinta matematica eu cred ca este de neacceptat.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Empty](https://2img.net/i/empty.gif) II. Aplicarea limetelor.
II. Aplicarea limetelor.
[Ne inchipuim ca nu stim nimic de rezultatele lui Euler]
Metodele astea constau in aceea ca sa exprimam o valoare deja cunoscuta (lungime, arie, etc.) prin necunoscuta pe care dorim sa o aflam, ajungem la o egalitate, din care ar trebui sa scoatem necunoscuta.
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Milii](https://2img.net/r/ihimizer/img826/144/milii.png)
Metoda cutare consta in aceea a exprima lungimea arcului (care deja cunoastem), prin functii trigonometrice.
Introducem elementul necunoscut: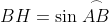 .
.
Raza eu am luat ca fiind 1, caci merge daca raportam mai departe la cerc cu lungime de orice alta lungime.
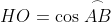
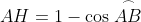
})
} {2}}})
} {2}}})
} {2}}}\right )^{2}+AD_{1}^{2}})
Acesta e primul "ciclu", deci vom avea la primul ciclu:
} {2}}}\right )^{2}+AD_{1}^{2}})
Urmeaza al doilea "ciclu", la care rezultatele sunt mai diochete, acolo deja vom avea o valoare si mai precisa de forma:
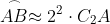
La altreilea "cilcu" o valoare si mai apropiata:
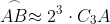
In final ajunjem la:
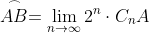
Si dupa ce calculam limita, din aceasta egalitate determinam necunoscuta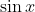 .
.

Metodele astea constau in aceea ca sa exprimam o valoare deja cunoscuta (lungime, arie, etc.) prin necunoscuta pe care dorim sa o aflam, ajungem la o egalitate, din care ar trebui sa scoatem necunoscuta.
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Milii](https://2img.net/r/ihimizer/img826/144/milii.png)
Metoda cutare consta in aceea a exprima lungimea arcului (care deja cunoastem), prin functii trigonometrice.
Introducem elementul necunoscut:
Raza eu am luat ca fiind 1, caci merge daca raportam mai departe la cerc cu lungime de orice alta lungime.
Acesta e primul "ciclu", deci vom avea la primul ciclu:
Urmeaza al doilea "ciclu", la care rezultatele sunt mai diochete, acolo deja vom avea o valoare si mai precisa de forma:
La altreilea "cilcu" o valoare si mai apropiata:
In final ajunjem la:
Si dupa ce calculam limita, din aceasta egalitate determinam necunoscuta
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Empty](https://2img.net/i/empty.gif) III. Aplicarea ruletelor
III. Aplicarea ruletelor
[Ne imaginam ca nimic nu stim de celelalte rezultate obtinute de dinainte]
Aceasta metoda mi se pare cea mai frumoasa metoda din toate.
Ideea consta in aceea ca in urma traectoriilor (si multe alte artificii) obtinute la miscarea unor corpuri rotunde sa aflam rezulatele.
Primul de unde se incepe e de la analiza cicloidei.
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Cycloidf1](https://2img.net/r/ihimizer/img16/7082/cycloidf1.gif)
Apare prima intrebare:
Cicloida este un sector de arc de cerc cu raza mai mare ca cercul initial?!
Eu cred ca da, si sint convins ca are o demonstratie foarte simpla.
Pentru o inchipuire mai buna:
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) 36865490](https://2img.net/r/ihimizer/img35/64/36865490.png)
Urmatorul pas e sa se analizeze trahoida exterioara si cea interioara:
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Trochoid1000](https://2img.net/r/ihimizer/img138/4585/trochoid1000.gif)
La fel si aici eu presupun ca pe deasupra axei OX traectoria trahoidei interioara reprezinta lungimea unui arc de cerc cu o raza mai mare, insa cu un unghi ce nu depaseste ~140*.
Invers este la trahoida exterioara, care inseamna lungimea unui arc de cerc cu o raza mai mare ca cercul din care se obtine trahoida exterioara.
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Writeup42](https://2img.net/r/ihimizer/img7/4129/writeup42.gif)
Sectorul albastru-cicloida [putin e gresit in desen].
Sectorul verde- trahoida exterioara.
Sectorul roz- trahoida interioara.
Se poate de lucrat atit cu trahoida interioara cit si exterioara.
Eu cred ca nu e nevoe sa ne complicam cu ambele, ci sa ne oprim la cea mai comoda varianta- trahoida interioara.
Si aici incepe problemita , caci stiind lungimea unui arc si raza cercului (mare) sa determinam: lungimea proectie trahoidei sau raza cercului din care s-a obtinut trahoida.
, caci stiind lungimea unui arc si raza cercului (mare) sa determinam: lungimea proectie trahoidei sau raza cercului din care s-a obtinut trahoida.
Iat' desenu care spune care e treaba:
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Trochoid1](https://2img.net/r/ihimizer/img40/575/trochoid1.gif)
Aceasta metoda mi se pare cea mai frumoasa metoda din toate.
Ideea consta in aceea ca in urma traectoriilor (si multe alte artificii) obtinute la miscarea unor corpuri rotunde sa aflam rezulatele.
Primul de unde se incepe e de la analiza cicloidei.
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Cycloidf1](https://2img.net/r/ihimizer/img16/7082/cycloidf1.gif)
Apare prima intrebare:
Cicloida este un sector de arc de cerc cu raza mai mare ca cercul initial?!
Eu cred ca da, si sint convins ca are o demonstratie foarte simpla.
Pentru o inchipuire mai buna:
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) 36865490](https://2img.net/r/ihimizer/img35/64/36865490.png)
Urmatorul pas e sa se analizeze trahoida exterioara si cea interioara:
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Trochoid1000](https://2img.net/r/ihimizer/img138/4585/trochoid1000.gif)
La fel si aici eu presupun ca pe deasupra axei OX traectoria trahoidei interioara reprezinta lungimea unui arc de cerc cu o raza mai mare, insa cu un unghi ce nu depaseste ~140*.
Invers este la trahoida exterioara, care inseamna lungimea unui arc de cerc cu o raza mai mare ca cercul din care se obtine trahoida exterioara.
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Writeup42](https://2img.net/r/ihimizer/img7/4129/writeup42.gif)
Sectorul albastru-cicloida [putin e gresit in desen].
Sectorul verde- trahoida exterioara.
Sectorul roz- trahoida interioara.
Se poate de lucrat atit cu trahoida interioara cit si exterioara.
Eu cred ca nu e nevoe sa ne complicam cu ambele, ci sa ne oprim la cea mai comoda varianta- trahoida interioara.
Si aici incepe problemita
Iat' desenu care spune care e treaba:
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Trochoid1](https://2img.net/r/ihimizer/img40/575/trochoid1.gif)
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Empty](https://2img.net/i/empty.gif) Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Re: Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta)
Dupa cum am mai spus, in plan sunt cel putin (se pare ca mai mult nici nu poate fi) 3 tipuri de sisteme de coordonate:
1) biaxalunghiular (cartezian); LUL... distanta dintre 2 puncte<=teorema lui Pitagora...
2) axalunghiular (coordonate polare);
3) segmentbiunghiular (un fel de paralaxa..).
Din toate cele 3 sisteme eu prefer pe al treilea.
Mai toata astronomia cu masurarile ei strict sta sub piciorul celei de a treia categorie de sisteme de coordonate.
Nimeni se va apuca de masurat distanta intre 2 puncte folosind prima categorie, caci aici nene trebue sa zbori pina in un colt de galactica- sa masiri distanta, si apoi in alt colt de galactica, si in sfirsit sa aplici teorema lui Pitagora.
Coordonatele polare nu sunt nici ele mai buna, aici trebue sa zbori numai in o directiem adica sa faci cel putin o masuratoare de asta negheoaba, si una mai breaza (masurarea unghiului..).
Cind vine vorba de coordonatele segmentbiunghiular, lucrurile se schimba.
Ai nevoe sa iti ei pe plac un segment cu o anumita lungime, si apoi sa faci 2 masuratori pe loc la capetele lui.
Aici cert ca nimic nu mai faci cu teorema lui Pitagora, si ai nevoe de cunoasterea bine si pina la capat a functiilor trigonometrice.
1) biaxalunghiular (cartezian); LUL... distanta dintre 2 puncte<=teorema lui Pitagora...
2) axalunghiular (coordonate polare);
3) segmentbiunghiular (un fel de paralaxa..).
Din toate cele 3 sisteme eu prefer pe al treilea.
Mai toata astronomia cu masurarile ei strict sta sub piciorul celei de a treia categorie de sisteme de coordonate.
Nimeni se va apuca de masurat distanta intre 2 puncte folosind prima categorie, caci aici nene trebue sa zbori pina in un colt de galactica- sa masiri distanta, si apoi in alt colt de galactica, si in sfirsit sa aplici teorema lui Pitagora.
Coordonatele polare nu sunt nici ele mai buna, aici trebue sa zbori numai in o directiem adica sa faci cel putin o masuratoare de asta negheoaba, si una mai breaza (masurarea unghiului..).
Cind vine vorba de coordonatele segmentbiunghiular, lucrurile se schimba.
Ai nevoe sa iti ei pe plac un segment cu o anumita lungime, si apoi sa faci 2 masuratori pe loc la capetele lui.
Aici cert ca nimic nu mai faci cu teorema lui Pitagora, si ai nevoe de cunoasterea bine si pina la capat a functiilor trigonometrice.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Left_bar_bleue](https://2img.net/i/fa/i/left_bar_bleue.jpg)


![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Right_bar_bleue](https://2img.net/i/fa/i/right_bar_bleue.jpg)
Puncte : 25855
Data de inscriere : 19/06/2011
 Subiecte similare
Subiecte similare» Dupa parerea mea.
» [Rezolvat]Problemă cu teoria gravitaţiei? NU. Problema este rezolvată în cazul nerelativist.
» Stiinta oficiala si stiinta neoficiala
» [Rezolvat]Problemă cu teoria gravitaţiei? NU. Problema este rezolvată în cazul nerelativist.
» Stiinta oficiala si stiinta neoficiala
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Facebook](https://2img.net/i/fa/social_bookmarking/facebook.gif) Devino fan Forumgratuit
Devino fan Forumgratuit ![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Probmil](https://2img.net/r/ihimizer/img6/4645/probmil.png)
![Problema mileniilor[dupa parerea mea] (una din cele mai importante probleme din stiinta) Egvha2rrmtiodigitalsign](https://2img.net/r/ihimizer/img708/6905/egvha2rrmtiodigitalsign.jpg)
