Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Forever_Man Ieri la 22:56
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la eugen în Global warming is happening?
( 1 )
» Mesaj de la CAdi în TEORIA CONSPIRATIEI NU ESTE UN MIT...
( 1 )
» Mesaj de la CAdi în Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12458) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Spune şi altora
Cine este conectat?
În total sunt 31 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 31 Vizitatori :: 1 Motor de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Cât de asemănătoare poate fi o elice circulară cu o dreaptă
4 participanți
Pagina 1 din 2
Pagina 1 din 2 • 1, 2 
 Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Elicea circulară este singura curbă care are curbura şi torsiunea constante. Ea se înfăşoară în jurul unui cilindru drept caracterizat de o anumită circumferinţă şi o anumită înălţime. În funcţie de aceşti doi parametri, elicea este mai mult sau mai puţin alungită, mai mult sau mai puţin groasă. O elice foarte alungită se înfăşoară în jurul unui cilindru de înălţime mare, iar o elice foarte groasă se înfăşoară în jurul unui cilindru de circumferinţă foarte mare.
Desigur, elicea circulară este o curbă nelimitată şi tocmai de aceea şi cilindrul pe care se înfăşoară ea va fi de asemenea nelimitat. Cu toate acestea, putem defini fără probleme înălţimea cilindrului ca fiind distanţa dintre două spire consecutive ale elicei circulare. Asta în ipoteza în care ştim ce este o spiră a elicei circulare. Dacă totuşi avem nevoie de o definiţie mai precisă a spirei elicei, atunci putem spune riguros că spira elicei circulare este porţiunea dintre cele mai apropiate două puncte de pe curbă în care tangentele la elice sunt paralele.
Aşadar, ştim ce este o spiră şi ştim că elicea circulară se înfăşoară în jurul unui cilindru drept de o anumită circumferinţă şi o anumită înălţime. Vrem acum să vedem ce se întâmplă cu elicea circulară dacă modificăm parametrii cilindrului pe care ea se înfăşoară. Mai exact, am vrea să ştim cam cum ar trebui să modificăm aceşti parametri astfel încât elicea circulară să se apropie cât mai mult de o dreaptă, să semene cât mai mult cu o dreaptă.
Pentru aceasta să acţionăm independent întâi asupra circumferinţei cilindrului, apoi asupra înălţimii sale. Haideţi, pentru început, să mărim foarte mult circumferinţa cilindrului. Ce se va întâmpla cu elicea circulară dacă mărim foarte mult circumferinţa? Dacă mărim foarte mult circumferinţa cilindrului, atunci un orice porţiune de pe suprafaţa cilindrului va începe să semene din ce în ce mai mult cu o porţiune dintr-un plan, curbura cilindrului şi implicit a elicei devenind din ce în ce mai mică. Prin urmare, mărind circumferinţa cilindrului, forma elicei se apropie din ce în ce mai mult de forma unei drepte. Iată deci un prim caz în care elicea seamănă foarte mult cu o dreaptă. Cât de mult? Oricât de mult vrem. Ba chiar atât de mult, încât să nu avem la dispoziţie nici un mijloc prin care să putem distinge elicea de o dreaptă. Altfel spus, există o limită superioară pentru circumferinţa cilindrului elicei dincolo de care elicea circulară poate fi considerată o dreaptă. Dar şi reciproc, orice dreaptă poate fi considerată astfel o elice circulară de circumferinţă suficient de mare, neexistând niciun criteriu practic prin care să putem distinge fără dubiu între o dreaptă şi o elice circulară de circumferinţă suficient de mare.
Oare mai există asemenea cazuri în care elicea circulară seamănă foarte mult cu o dreaptă? Da, mai există asemenea cazuri. Bunăoară, să analizăm acum cazul în care circumferinţa cilindrului elicei este de data aceasta extrem de mică. Ce se întâmplă în acest caz? Păi, în acest caz cilindrul devine extrem de subţire, atât de subţire, încât elicea circulară ce se înfăşoară în jurul unui asemenea cilindru începe să semene din ce în ce mai mult cu axa cilindrului respectiv, care este evident o dreaptă. Practic, există o limită inferioară a circumferinţei sub care nu mai putem face distincţie clară între elicea circulară şi axa cilindrului şi ajungem să le confundăm datorită apropierii dintre ele.
Ambele cazuri analizate mai sus au fost independente de valoarea înălţimii cilindrului elicei. Indiferent ce valoare fixată (foarte mică sau foarte mare) ar avea înălţimea cilindrului, există o limită superioară şi una inferioară pentru valoarea circumferinţei, dincolo de care elicea circulară nu poate fi deosebită de o dreaptă. Reciproc, tot ceea ce pare a fi o dreaptă ar putea fi la fel de bine de fapt o elice circulară înfăşurată pe un cilindru de rază extrem de mare sau extrem de mică.
În fine, mai există un caz în care nu putem spune dacă este vorba despre o elice circulară sau despre o dreaptă: cazul în care înălţimea cilindrului este enormă. În acest caz, orice valoare ar avea circumferinţa cilindrului, elicea circulară face un unghi foarte mic cu axa cilindrului şi putem alege o valoare atât de mare pentru înălţimea cilindrului, încât practic să nu mai putem observa vreo valoare nenulă pentru unghiul elicei şi în consecinţă să nu mai putem distinge dacă privim o elice sau privim o dreaptă.
Cazul elicei de înălţime foarte mică este irelevant, căci nu putem confunda o asemenea elice cu o dreaptă în toate cazurile. Mai exact, chiar dacă înălţimea elicei este nulă, pentru circumferinţe mici se observă deosebirea clară dintre elicea circulară (devenită tocmai cerc) şi o dreaptă.
De altfel, toate raţionamentele noastre anterioare sunt sintetizate în formula care ne dă expresia curburii elicei circulare în funcţie de raza a a cilindrului şi pasul (barat) b al acestuia.
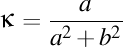 .
.
Mai exact, ştiind că o dreaptă are curbura nulă, este suficient să observăm că pentru valorile foarte mari sau foarte mici ale circumferinţei, respectiv, pentru valori foarte mari ale înălţimii, curbura elicei circulare tinde spre zero.
Astfel, avem cele trei cazuri relevante:
-1). Cazul circumferinţei foarte mari, deci cazul în care a tinde la infinit. Numesc acest caz, cazul elicei groase.
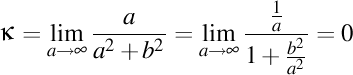 .
.
-2). Cazul circumferinţei foarte mici, deci cazul în care a tinde la zero. Vorbim astfel despre elicea subţire.
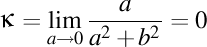 .
.
-3). Cazul înălţimii foarte mari, deci cazul în care b tinde la infinit. În acest caz spun că este vorba despre elicea înaltă (lăsând loc pentru a numi elice scurtă pe aceea a cărei spiră este scurtă şi elice scundă pe aceea a cărei înălţime este mică, cele două tipuri de elice posibile nefiind identice (elicea scundă nu este neapărat şi elice scurtă)).
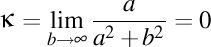 .
.
Aşadar, dragii mei cititori, elicea foarte groasă sau foarte subţire sau foarte înaltă poate fi confundată uşor cu o dreaptă. Şi reciproc, pentru orice presupusă dreaptă trebuie să fim conştienţi de posibilitatea noastră de a ne înşela în privinţa ei, având mereu prezent în minte dubiul că s-ar putea ca "dreapta" din faţa noastră să fie de fapt tocmai o elice circulară (foarte groasă, foarte subţire sau foarte înaltă). Şi atunci, dragi cititori, cât de justificat vi se mai pare principiul actual al inerţiei care spune că un corp liber se deplasează rectiliniu? Cât de siguri putem fi pe extrapolarea făcută de Galilei când a studiat corpuri aruncate pe suprafeţe din ce în ce mai netede, extrapolare pe care o mai menţinem încă şi astăzi fără rezerve? Nu cumva corpurile lui se deplasau de fapt mai degrabă pe elice circulare (foarte groase sau foarte subţiri sau foarte înalte) decât strict, strict rectiliniu?
Desigur, elicea circulară este o curbă nelimitată şi tocmai de aceea şi cilindrul pe care se înfăşoară ea va fi de asemenea nelimitat. Cu toate acestea, putem defini fără probleme înălţimea cilindrului ca fiind distanţa dintre două spire consecutive ale elicei circulare. Asta în ipoteza în care ştim ce este o spiră a elicei circulare. Dacă totuşi avem nevoie de o definiţie mai precisă a spirei elicei, atunci putem spune riguros că spira elicei circulare este porţiunea dintre cele mai apropiate două puncte de pe curbă în care tangentele la elice sunt paralele.
Aşadar, ştim ce este o spiră şi ştim că elicea circulară se înfăşoară în jurul unui cilindru drept de o anumită circumferinţă şi o anumită înălţime. Vrem acum să vedem ce se întâmplă cu elicea circulară dacă modificăm parametrii cilindrului pe care ea se înfăşoară. Mai exact, am vrea să ştim cam cum ar trebui să modificăm aceşti parametri astfel încât elicea circulară să se apropie cât mai mult de o dreaptă, să semene cât mai mult cu o dreaptă.
Pentru aceasta să acţionăm independent întâi asupra circumferinţei cilindrului, apoi asupra înălţimii sale. Haideţi, pentru început, să mărim foarte mult circumferinţa cilindrului. Ce se va întâmpla cu elicea circulară dacă mărim foarte mult circumferinţa? Dacă mărim foarte mult circumferinţa cilindrului, atunci un orice porţiune de pe suprafaţa cilindrului va începe să semene din ce în ce mai mult cu o porţiune dintr-un plan, curbura cilindrului şi implicit a elicei devenind din ce în ce mai mică. Prin urmare, mărind circumferinţa cilindrului, forma elicei se apropie din ce în ce mai mult de forma unei drepte. Iată deci un prim caz în care elicea seamănă foarte mult cu o dreaptă. Cât de mult? Oricât de mult vrem. Ba chiar atât de mult, încât să nu avem la dispoziţie nici un mijloc prin care să putem distinge elicea de o dreaptă. Altfel spus, există o limită superioară pentru circumferinţa cilindrului elicei dincolo de care elicea circulară poate fi considerată o dreaptă. Dar şi reciproc, orice dreaptă poate fi considerată astfel o elice circulară de circumferinţă suficient de mare, neexistând niciun criteriu practic prin care să putem distinge fără dubiu între o dreaptă şi o elice circulară de circumferinţă suficient de mare.
Oare mai există asemenea cazuri în care elicea circulară seamănă foarte mult cu o dreaptă? Da, mai există asemenea cazuri. Bunăoară, să analizăm acum cazul în care circumferinţa cilindrului elicei este de data aceasta extrem de mică. Ce se întâmplă în acest caz? Păi, în acest caz cilindrul devine extrem de subţire, atât de subţire, încât elicea circulară ce se înfăşoară în jurul unui asemenea cilindru începe să semene din ce în ce mai mult cu axa cilindrului respectiv, care este evident o dreaptă. Practic, există o limită inferioară a circumferinţei sub care nu mai putem face distincţie clară între elicea circulară şi axa cilindrului şi ajungem să le confundăm datorită apropierii dintre ele.
Ambele cazuri analizate mai sus au fost independente de valoarea înălţimii cilindrului elicei. Indiferent ce valoare fixată (foarte mică sau foarte mare) ar avea înălţimea cilindrului, există o limită superioară şi una inferioară pentru valoarea circumferinţei, dincolo de care elicea circulară nu poate fi deosebită de o dreaptă. Reciproc, tot ceea ce pare a fi o dreaptă ar putea fi la fel de bine de fapt o elice circulară înfăşurată pe un cilindru de rază extrem de mare sau extrem de mică.
În fine, mai există un caz în care nu putem spune dacă este vorba despre o elice circulară sau despre o dreaptă: cazul în care înălţimea cilindrului este enormă. În acest caz, orice valoare ar avea circumferinţa cilindrului, elicea circulară face un unghi foarte mic cu axa cilindrului şi putem alege o valoare atât de mare pentru înălţimea cilindrului, încât practic să nu mai putem observa vreo valoare nenulă pentru unghiul elicei şi în consecinţă să nu mai putem distinge dacă privim o elice sau privim o dreaptă.
Cazul elicei de înălţime foarte mică este irelevant, căci nu putem confunda o asemenea elice cu o dreaptă în toate cazurile. Mai exact, chiar dacă înălţimea elicei este nulă, pentru circumferinţe mici se observă deosebirea clară dintre elicea circulară (devenită tocmai cerc) şi o dreaptă.
De altfel, toate raţionamentele noastre anterioare sunt sintetizate în formula care ne dă expresia curburii elicei circulare în funcţie de raza a a cilindrului şi pasul (barat) b al acestuia.
Mai exact, ştiind că o dreaptă are curbura nulă, este suficient să observăm că pentru valorile foarte mari sau foarte mici ale circumferinţei, respectiv, pentru valori foarte mari ale înălţimii, curbura elicei circulare tinde spre zero.
Astfel, avem cele trei cazuri relevante:
-1). Cazul circumferinţei foarte mari, deci cazul în care a tinde la infinit. Numesc acest caz, cazul elicei groase.
-2). Cazul circumferinţei foarte mici, deci cazul în care a tinde la zero. Vorbim astfel despre elicea subţire.
-3). Cazul înălţimii foarte mari, deci cazul în care b tinde la infinit. În acest caz spun că este vorba despre elicea înaltă (lăsând loc pentru a numi elice scurtă pe aceea a cărei spiră este scurtă şi elice scundă pe aceea a cărei înălţime este mică, cele două tipuri de elice posibile nefiind identice (elicea scundă nu este neapărat şi elice scurtă)).
Aşadar, dragii mei cititori, elicea foarte groasă sau foarte subţire sau foarte înaltă poate fi confundată uşor cu o dreaptă. Şi reciproc, pentru orice presupusă dreaptă trebuie să fim conştienţi de posibilitatea noastră de a ne înşela în privinţa ei, având mereu prezent în minte dubiul că s-ar putea ca "dreapta" din faţa noastră să fie de fapt tocmai o elice circulară (foarte groasă, foarte subţire sau foarte înaltă). Şi atunci, dragi cititori, cât de justificat vi se mai pare principiul actual al inerţiei care spune că un corp liber se deplasează rectiliniu? Cât de siguri putem fi pe extrapolarea făcută de Galilei când a studiat corpuri aruncate pe suprafeţe din ce în ce mai netede, extrapolare pe care o mai menţinem încă şi astăzi fără rezerve? Nu cumva corpurile lui se deplasau de fapt mai degrabă pe elice circulare (foarte groase sau foarte subţiri sau foarte înalte) decât strict, strict rectiliniu?
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Lumina strabate miliarde de ani, de la marginile universului pana la noi, pastrand nealterate imaginile stelelor si ale galaxiilor cele mai indepartate. Asadar nu degeaba se spune ca traiectoria luminii este o linie dreapta, atunci cand nu este perturbata de campuri. Orice corp a carui traiectorie se suprapune cu cea a luminii se spune ca are o traiectorie rectilinie. Cum corpurile sunt puternic influientate de campuri, traiectoria acestora poate lua orice forma in functie de configuratia campurilor, si a miscarii surselor acestora.Şi atunci, dragi cititori, cât de justificat vi se mai pare principiul actual al inerţiei care spune că un corp liber se deplasează rectiliniu?
Demonstratia degenerarii elicei in cercuri sau drepte, este evidenta si nimeni nu se indoieste de aceasta. Indoiala provine din utilitatea aplicarii in fizica a acestor transformari, din moment ce se ajunge la acelasi lucru pornind de la elipsa sau dreapta. Cand se va ajunge la navigatii intergalactice, probabil vom fi interesati de traiectorii cicloidale mai mult decat elicoidale, deoarece evolutia stelelor se produce in planul ecuatorial al galaxiei, stelele descriind niste cicloide si nicidecum elicoide. Insa in lumea submicrocosmica cred ca se aplica traiectoria elicoidala descrisa de punctele materiale asociate particulelor.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Virgil, n-ai luat în calcul posibilitatea ca lumina să se deplaseze pe o elice foarte subţire. În acest caz, oricâte miliarde de ani ar merge ea, tot asemănătoare cu axa elicei va fi, deci tot dreaptă ţi se va părea.
Dacă n-ai înţeles încă elicea subţire, mai apleacă-ţi o dată mintea asupra primului mesaj.
Dacă n-ai înţeles încă elicea subţire, mai apleacă-ţi o dată mintea asupra primului mesaj.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Ce crezi ca asa mare filozofie este? Lumina polarizata isi pastreaza planul de polarizare mult si bine, ori daca ar fi mers pe o elice si-ar fi rotit planul de polarizare in timp. Am mai specificat acest lucru si cu alte ocazii. Cel mult fiecare "luxon" din lumea subcuantica care creaza fluidul stringurilor, sa aiba o miscare elicoidala asa cum rezulta din justificarea masei relativiste pe care am aratat-o de cateva ori.Abel Cavaşi a scris:Virgil, n-ai luat în calcul posibilitatea ca lumina să se deplaseze pe o elice foarte subţire. În acest caz, oricâte miliarde de ani ar merge ea, tot asemănătoare cu axa elicei va fi, deci tot dreaptă ţi se va părea.
Dacă n-ai înţeles încă elicea subţire, mai apleacă-ţi o dată mintea asupra primului mesaj.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Poţi să demonstrezi această afirmaţie? Arată-mi legătura dintre mişcarea pe elice şi planul de polarizare.virgil a scris:Lumina polarizata isi pastreaza planul de polarizare mult si bine, ori daca ar fi mers pe o elice si-ar fi rotit planul de polarizare in timp.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Daca de exemplu am polarizat vertical raza de lumina, pe ecran apare o dunga verticala. Daca lumina are o axa de rotatie dealungul traiectoriei, atunci dupa un parcurs dunga verticala ar trebui sa devina o dunga inclinata fata de vericala. ori acest lucru nu se intampla. De altfel si la undele TV care sunt polarizate intr-un plan isi pastreaza planul de polarizare in timp.Abel Cavaşi a scris:Poţi să demonstrezi această afirmaţie? Arată-mi legătura dintre mişcarea pe elice şi planul de polarizare.virgil a scris:Lumina polarizata isi pastreaza planul de polarizare mult si bine, ori daca ar fi mers pe o elice si-ar fi rotit planul de polarizare in timp.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Arată-mi mecanismul prin care se întâmplă asta, ca să nu rămână doar o vorbă goală.virgil a scris:Daca lumina are o axa de rotatie dealungul traiectoriei, atunci dupa un parcurs dunga verticala ar trebui sa devina o dunga inclinata fata de vericala.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Hai mai întâi să înțelegem la ce ne referim când vorbim de curbura elicei.
S-o luăm băbește, că așa înțelege toată lumea.
Oricum, din modul în care te-ai exprimat și te exprimi, curbura elicei nu poate fi curbura cilindrului, din notațiile tale.
N-ar mai avea sens atâta analiză.
Avem un arc pe care-l ținem de capetele sale cu ambele mâini.
Acel arc este o elice.
Dacă spirele arcului sunt lipite una de alta, am putea spune că pasul, b din notațiile tale, este 0.
Dacă tragem de arc, spirele se depărtează una de alta, uniform presupunem, iar pasul elicei, valoarea b, va crește.
Ceea ce vom vedea 2D în fața noastră este o sinusoidă, mai alungită sau mai strânsă.
Această sinusoidă este curbura elicei (?) :

unde distanța dintre două vârfuri consecutive pe orizontală este pasul b, iar distanța dintre linia centrală și un vârf este raza a.
S-o luăm băbește, că așa înțelege toată lumea.
Oricum, din modul în care te-ai exprimat și te exprimi, curbura elicei nu poate fi curbura cilindrului, din notațiile tale.
N-ar mai avea sens atâta analiză.
Avem un arc pe care-l ținem de capetele sale cu ambele mâini.
Acel arc este o elice.
Dacă spirele arcului sunt lipite una de alta, am putea spune că pasul, b din notațiile tale, este 0.
Dacă tragem de arc, spirele se depărtează una de alta, uniform presupunem, iar pasul elicei, valoarea b, va crește.
Ceea ce vom vedea 2D în fața noastră este o sinusoidă, mai alungită sau mai strânsă.
Această sinusoidă este curbura elicei (?) :

unde distanța dintre două vârfuri consecutive pe orizontală este pasul b, iar distanța dintre linia centrală și un vârf este raza a.
Ultima editare efectuata de catre curiosul in Lun 12 Aug 2013, 21:03, editata de 1 ori (Motiv : corectat raza a- in curbura cilindrului.)
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Ce mecanism vrei? nu stii cum se face polarizarea luminii?Abel Cavaşi a scris:Arată-mi mecanismul prin care se întâmplă asta, ca să nu rămână doar o vorbă goală.virgil a scris:Daca lumina are o axa de rotatie dealungul traiectoriei, atunci dupa un parcurs dunga verticala ar trebui sa devina o dunga inclinata fata de vericala.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
De acord, dar nici n-am susţinut egalitatea lor. În ultimă instanţă, curbura totală a suprafeţei cilindrului este mereu nulă, indiferent de raza cilindrului. Distincţia o facem între curbura bazei cilindrului (care este un cerc) şi curbura elicei. Oricum, curbura elicei este cea dată de formulă, deci intervenţia ta nu a contestat încă posibilitatea de care vorbesc, de a face confuzie între elicea circulară şi dreaptă.curiosul a scris:curbura elicei nu poate fi curbura cilindrului
Virgil, nu ţi-am cerut mecanismul polarizării, ci ţi-am cerut să descrii cum depinde "dunga" de mişcarea elicoidală. Ia gândeşte-te la următorul aspect: dunga depinde de proiecţia traiectoriei pe un plan longitudinal. Şi mai ţine seamă de faptul că nu există polarizare perfect verticală, ci doar mai mult sau mai puţin eliptică.virgil a scris:Ce mecanism vrei? nu stii cum se face polarizarea luminii?Abel Cavaşi a scris:Arată-mi mecanismul prin care se întâmplă asta, ca să nu rămână doar o vorbă goală.virgil a scris:Daca lumina are o axa de rotatie dealungul traiectoriei, atunci dupa un parcurs dunga verticala ar trebui sa devina o dunga inclinata fata de vericala.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă


Sa presupunem ca asa arata o elicoida polarizata vertical. Daca raza de lumina ar continua sa se roteasca in jurul axei, atunci liniile verticale ce indica maximul campului electromagnetic, ar trebui sa iese din planul vertical si sa se incline. In aceasta situatie lumina ar putea fi polarizata intr-un plan care sufera mereu o rotatie dealungul axei, ceia ce nu se constata indiferent la ce distanta punem un ecran perpendicular pe raza.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Vezi ce iese dacă faci confuzie între elice şi elicoidă? Faci tot felul de supoziţii care ies în evidenţă după discuţii îndelungate.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Explica-mi tu cum se face ca in urma polarizarii, apare o dunga verticala?Abel Cavaşi a scris:Vezi ce iese dacă faci confuzie între elice şi elicoidă? Faci tot felul de supoziţii care ies în evidenţă după discuţii îndelungate.
Cred ca tu nu-ti imaginezi cum variaza vectorul camp magnetic si camp electric. Daca ar fi o elice, atunci campul s-ar reduce la un punct, deoarece fiind o unda plana intersectia dintre un plan perpendicular pe elice, si elice, este doar un punct. In acest caz ce s-ar mai polariza, in loc de o dunga vericala, ar aparea un punct sus si unul jos.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Noa, aşa îmi place! Când începi să aprofundezi lucrurile îmi place. Lumina liberă nu este polarizată, Virgile. Sau nu în sensul actual al polarizării. Lumina se polarizează doar când se izbeşte de ceva, dar aia nu mai este lumină liberă, deci nu mai merge pe o elice circulară cum spune principiul elicoidal al inerţiei. Cel puţin, aşa îmi imaginez eu acum.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Nu se izbeste, doar se strecoara, una din metodele de polarizare este trecerea luminii printr-o retea de fante, precum o pana de porumbel. Insa raspunsul tau nu este bun, trebuie sa mai faci sapaturi.Lumina se polarizează doar când se izbeşte de ceva, dar aia nu mai este lumină liberă,
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Crezi ce vrei. Eu am demonstrat ce am vrut să demonstrez: că ne putem înşela atunci când credem că o traiectorie este dreaptă.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Nu ai demonstrat nimic, doar ai postulat. Ai zis; sa fie elicoidal, de parca ai fi D-zeu sa zici; sa fie lumina...Abel Cavaşi a scris:Crezi ce vrei. Eu am demonstrat ce am vrut să demonstrez: că ne putem înşela atunci când credem că o traiectorie este dreaptă.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Nici măcar asta n-ai înţeles? În acest topic am demonstrat, cu formule chiar, că putem face foarte uşor confuzie între o dreaptă şi o elice. Într-adevăr, în alt topic am formulat postulatul elicoidal al inerţiei, dar aia e altă mâncare de peşte.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Am inteles ca dupa parerea ta, daca traiectoriile in extremis se pot confunda, inseamna ca musai nu este o confuzie, ci chiar asa este. Dar acest lucru nu inseamna demonstratie, atat timp cat nici un experiment fizic nu confirma acest lucru.Abel Cavaşi a scris:Nici măcar asta n-ai înţeles? În acest topic am demonstrat, cu formule chiar, că putem face foarte uşor confuzie între o dreaptă şi o elice. Într-adevăr, în alt topic am formulat postulatul elicoidal al inerţiei, dar aia e altă mâncare de peşte.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Ba dimpotrivă, orice experiment ai face, tot nu poţi extrapola că o curbă este cu certitudine o dreaptă. Întotdeauna poţi avea dubiul că un experiment mai precis ar putea revela curbura nenulă a curbei.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Dar poti demonstra daca traiectoria unei pietre este o elice sau o parabola.Abel Cavaşi a scris:Ba dimpotrivă, orice experiment ai face, tot nu poţi extrapola că o curbă este cu certitudine o dreaptă. Întotdeauna poţi avea dubiul că un experiment mai precis ar putea revela curbura nenulă a curbei.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Sfatul meu este să încetezi să mai crezi că natura mişcă vreun corp pe o traiectorie ciudată, fără torsiune. Dimpotrivă, toate corpurile se mişcă pe traiectorii regulate, care au torsiunea nenulă.
În Fizica viitorului torsiunea va fi un termen foarte des utilizat. Neglijarea torsiunii este cel mai mare handicap al Ştiinţei contemporane.
În Fizica viitorului torsiunea va fi un termen foarte des utilizat. Neglijarea torsiunii este cel mai mare handicap al Ştiinţei contemporane.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Datorita neglijarii torsiunii, nu functioneaza bine internetul, navetele spatiale, GPS-ul, telescopul Huble, si cele peste 40 de sonde spatiale trimise in misiuni de cercetare.În Fizica viitorului torsiunea va fi un termen foarte des utilizat. Neglijarea torsiunii este cel mai mare handicap al Ştiinţei contemporane.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Avansul tehnologic nu probează veridicitatea unei teorii. Deşi oamenii primitivi foloseau de zor focul, habar n-aveau ce este acesta. Virgil, Virgil...
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Abel, din moment ce cazurile particulare de elicii apar ca şi drepte, cu ce ne ajută faptul că generalizarea unor traiectorii, care, până la urmă se dovedesc a fi tot drepte, le luăm orginal ca elicoidale? Nu că n-ar fi corect, dar nu ţi se pare un calcul în plus, o complicaţie a fizicii, care, până la urmă, se rezumă tot la principiile actuale?
_________________
Eşti inteligent atunci când crezi doar jumătate din ceea ce afli; eşti înţelept atunci când ştii care jumătate!

Razvan- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 6183




Puncte : 33836
Data de inscriere : 18/03/2011
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Dar tocmai asta este, Răzvane, că nu se dovedesc a fi drepte!
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Ce "nu se dovedesc a fi drepte", din moment ce geodezicele spaţiului nostru, ale universului, sun tocmai drepte?
_________________
Eşti inteligent atunci când crezi doar jumătate din ceea ce afli; eşti înţelept atunci când ştii care jumătate!

Razvan- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 6183




Puncte : 33836
Data de inscriere : 18/03/2011
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Cum dovedeşti că "sunt tocmai drepte", din moment ce poţi confunda uşor trei tipuri de elice circulară cu o dreaptă?
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Cosmologic, bazat pe interpretările datelor observaţionale, s-a ajuns la concluzia că raza de curbură a universului este zero, deci metrica lui este cea a unui spaţiu euclidian plat. Fapt ce rezultă ca şi caz particular al fizicii elicoidale.
Şi o altă întrebare: cum apare principiul minimei acţiuni prin prisma fizicii elicoidale? Nu cumva se reduce tot la o line dreaptă?
Atunci, de ce să ne complicăm? Eu nu văd rostul.
Ah! Că vrei tu să generalizezi ecuaţiile mişcării, care, până la urmă, se reduc tot la ecuaţia unei drepte? Sau, cum a mai spus, dacă într-adevăr ţinând cont de influenţele locale gravitaţionale, pot exista traiectorii elicoidale, acestea în nici un caz nu-şi vor păstra constantă curbura şi torsiunea, ele variind în funcţie de potenţialul gravitaţional respectiv.
Şi o altă întrebare: cum apare principiul minimei acţiuni prin prisma fizicii elicoidale? Nu cumva se reduce tot la o line dreaptă?
Atunci, de ce să ne complicăm? Eu nu văd rostul.
Ah! Că vrei tu să generalizezi ecuaţiile mişcării, care, până la urmă, se reduc tot la ecuaţia unei drepte? Sau, cum a mai spus, dacă într-adevăr ţinând cont de influenţele locale gravitaţionale, pot exista traiectorii elicoidale, acestea în nici un caz nu-şi vor păstra constantă curbura şi torsiunea, ele variind în funcţie de potenţialul gravitaţional respectiv.
_________________
Eşti inteligent atunci când crezi doar jumătate din ceea ce afli; eşti înţelept atunci când ştii care jumătate!

Razvan- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 6183




Puncte : 33836
Data de inscriere : 18/03/2011
 Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Re: Cât de asemănătoare poate fi o elice circulară cu o dreaptă
Tu vrei să-mi impui cu forţa "demonstraţia" asta? Care interpretări? Şi cât de justificate sunt ele, din moment ce nu putem distinge clar o dreaptă de o elice?Razvan a scris:bazat pe interpretările datelor observaţionale, s-a ajuns la concluzia că raza de curbură a universului este zero
Întrebarea e atât de bună, încât merită un topic separat. Dar deocamdată vreau să înţelegeţi în mod clar că putem să ne înşelăm amarnic atunci când credem că traiectoria unui corp este tocmai o dreaptă. Singurul lucru care merge în linie dreaptă este lumina în vid (lancretianul traiectoriei sale este nul).Şi o altă întrebare: cum apare principiul minimei acţiuni prin prisma fizicii elicoidale? Nu cumva se reduce tot la o line dreaptă?
Pagina 1 din 2 • 1, 2 
 Subiecte similare
Subiecte similare» Mai bine porțiuni de elice circulară decât segmente de dreaptă
» Transformări care invariază o elice circulară
» Cum se măsoară pasul unei elice?
» Transformări care invariază o elice circulară
» Cum se măsoară pasul unei elice?
Pagina 1 din 2
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 
