Mai bine porțiuni de elice circulară decât segmente de dreaptă

Știm că astăzi se aproximează curbele prin segmente de dreaptă. Adică, se presupune că pe porțiuni suficient de mici, curbele pot fi aproximate prin segmente de dreaptă. Dar se știe că dreapta este o curbă ciudată, având curbura nulă și torsiunea nedeterminată.

   Dar eu vă propun acum altceva. Cum orice curbă obișnuită (netedă) are curbură și torsiune, ar fi mai eficient să presupunem că pe porțiuni suficient de mici curbura și torsiunea curbelor respective este constantă. Și cum o curbă având curbura și torsiunea constante este o elice circulară, rezultă că pe porțiuni suficient de mici putem aproxima o curbă cu o elice circulară.

   Așadar, putem admite că o particulă care se mișcă pe o curbă oarecare se mișcă, de fapt, pe o elice circulară un interval scurt de timp, după care „suferă o ciocnire” care ciocnire modifică parametrii elicei circulare pe care urmează să se deplaseze. Și procesul se repetă oricât de des dorim noi. Cu cât vom alege o diviziune mai fină a curbei, deci cu cât o vom separa în mai multe bucățele, cu atât aproximarea curbei prin elice circulare va fi mai eficientă.

   Și cum o elice circulară este determinată de două numere reale (curbura și torsiunea) putem admite că aceste două numere reale constituie tocmai un număr complex. Asta înseamnă atunci că unei porțiuni mici a unei curbe îi putem asocia un număr complex, asocierea fiind cu atât mai precisă cu cât divizăm curba în mai multe porțiuni.

   Oare ce salt în cunoaștere ar reprezenta trecerea de la aproximarea curbelor prin segmente de dreaptă la aproximarea curbelor prin elice circulare?

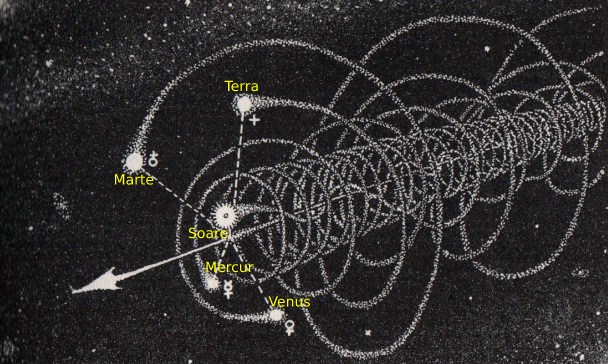
Problema miscarii elicoidale presupune existenta a doua campuri suprapuse. Odata este campul gravitational al Soarelui in jurul caruia se invart planetele descriind orbite plane care au torsiunea zero, apoi urmeaza miscarea Soarelui in jurul Galaxiei, care transforma orbitele planetelor in traiectorii elicoidale introducand torsiunea diferita de zero. De fapt aceiasi traiectorie a planetelor privita dintr-un sistem de observare legat de sistemul solar, constata ca planetele se misca pe orbite curbe plane, in timp ce un alt sistem de observare legat de galaxie constata ca planetele se misca pe traiectorii elicoidale avand torsiunea diferita de zero.

Așa este. Există mărimi fizice care depind de observator. La fel este și cu curbura și torsiunea. Mai mult, trecerea de la un observator la altul poate fi descrisă frumos, matematic și nu se desfășoară haotic.

Abel Cavaşi a scris:Știm că astăzi se aproximează curbele prin segmente de dreaptă. Adică, se presupune că pe porțiuni suficient de mici, curbele pot fi aproximate prin segmente de dreaptă. Dar se știe că dreapta este o curbă ciudată, având curbura nulă și torsiunea nedeterminată.

Daca nu dorim sa facem la limita aproximatia cu segmentele de
dreapta, putem aproxima curba prin segmente de curba(cerc).

   Dar eu vă propun acum altceva. Cum orice curbă obișnuită (netedă) are curbură și torsiune, ar fi mai eficient să presupunem că pe porțiuni suficient de mici curbura și torsiunea curbelor respective este constantă. Și cum o curbă având curbura și torsiunea constante este o elice circulară, rezultă că pe porțiuni suficient de mici putem aproxima o curbă cu o elice circulară.

(neteda) inseamna plana ? Cine a spus ca o curba plana
are torsiune ? Acolo unde introduci un postulat(axioma?)
in cercetarea ta, trebuie sa anunti daca esti serios!

 Așadar, putem admite că o particulă care se mișcă pe o curbă oarecare se mișcă, de fapt, pe o elice circulară un interval scurt de timp, după care „suferă o ciocnire” care ciocnire modifică parametrii elicei circulare pe care urmează să se deplaseze. Și procesul se repetă oricât de des dorim noi. Cu cât vom alege o diviziune mai fină a curbei, deci cu cât o vom separa în mai multe bucățele, cu atât aproximarea curbei prin elice circulare va fi mai eficientă.

Fiindca contextul este foarte fragil, ar trebui sa precizezi mereu
daca este vorba de o curba plana sau una in spatiu.

  Și cum o elice circulară este determinată de două numere reale (curbura și torsiunea) putem admite că aceste două numere reale constituie tocmai un număr complex. Asta înseamnă atunci că unei porțiuni mici a unei curbe] îi putem asocia un număr complex, asocierea fiind cu atât mai precisă cu cât divizăm curba în mai multe porțiuni.

Plana sau spatiala ?

 Oare ce salt în cunoaștere ar reprezenta trecerea de la aproximarea curbelor prin segmente de dreaptă la aproximarea curbelor prin elice circulare?

Care dintre curbe?
Iar discutam mult despre geometrie ca sa tragem concluzii despre
miscare ?

Hello, what an amazing observation. I do not know the exact answer. When a charged particle enters a magnetic field at an angle other than 90 degrees, one component of its velocity causes it to move in a linear direction, while the other causes it to move in a circular direction, resulting in a helical motion. A helical route is formed when the particle's velocity has components that are parallel and perpendicular to the uniform magnetic field. There is no force on the particle in the parallel case, but there is a centripetal acceleration toward the center in the perpendicular case. There are physical quantities that are subject to the observer's perspective. Curvature and torsion are the same way.

Abel Wells a scris:Hello, what an amazing observation....
There are physical quantities that are subject to the observer's perspective

Nu e niciun fel de "amazing observation", ci doar de "observer's perspective"!

Abel Wells a scris:Hello, what an amazing observation. I do not know the exact answer. When a charged particle enters a magnetic field at an angle other than 90 degrees, one component of its velocity causes it to move in a linear direction, while the other causes it to move in a circular direction, resulting in a helical motion. A helical route is formed when the particle's velocity has components that are parallel and perpendicular to the uniform magnetic field. There is no force on the particle in the parallel case, but there is a centripetal acceleration toward the center in the perpendicular case. There are physical quantities that are subject to the observer's perspective. Curvature and torsion are the same way.

Combinatia aceasta de ABEL (CAVASI) si (H.G.) WELLS ma face
sa cred ca utilizatorul este un compatriot de-al nostru de origine
maghiara, care nu are la el toata limba romana. Altfel dece s-ar
stradui sa ne obstructioneze ?
Nu ne-am supara noi pentru cate o greseala gramaticala, fiindca
n-ar fi singurul. Poate n-a citit cum scrie Meteor !
Curiosule, ai un bun prilej cu utilizatorul "x" ! Ii poti acorda o nota
buna la limba engleza ? Sau la asta si tu esti cam... maghiar ?
Cat despre portiunile cu care asimilezi o curba, in domeniul
infinitesimal cu cat devin mai mici, toate se apropie de punct si
trebuie sa obtii acelasi rezultat.