Cazul n=p, p prim impar al teoremei lui Fermat

O demonstrație completă a teoremei lui Fermat impune doar demonstrarea cazurilor pentru care n este egal cu 4 și n este un număr prim impar. Vis-a-vis de acest caz, unde n este un număr prim impar, cred că pot aduce ecuația la o formă interesantă, care ar putea aduce ceva în plus în încercarea unei demonstrații generale a acestui caz.

Putrem să scriem pe rând ecuația în trei moduri, deoarece p este prim impar :







În continuare putem demonstra că dezvoltarea celor două diferențe și a sumei prin această metodă, factorii produsului reprezentați de cele două paranteze din dreapta pot avea ca și factor comun doar p. În cazul diferențelor, demonstrația a fost făcută foarte frumos de Mezei Geza prin teorema împărțirii cu rest a polinoamelor, care poate fi folosită și pentru a demonstra acest lucru în cazul sumei.
Există și o altă modalitate prin care putem demonstra acest aspect, prin scrierea diferită a dezvoltării sumei și diferențelor respective.
Voi scrie mai întâi cazurile simple pentru a se înțelege mai bine.
n=3







În toate cazurile, în paranteza mai mare din dreapta poate fi scos factor comun paranteza mică. În toate cazurile, în paranteza mare, termenul care rămâne și termenul care are ca factor de paranteza mică, pot avea unic factor comun doar 3, deoarece x, y, z sunt considerate toate prime între ele. Dacă y și (z-y) au un factor comun spre exemplu, atunci z îl va avea de asemenea, iar asta este imposibil dacă z și y sunt prime între ele. Deci singurul factor comun al celor două paranteze poate fi doar 3.

cazul n=5



identic pentru cealaltă diferență și



În mod similar se demonstrează că singurul factor al celor două paranteze poate fi doar 5, precum și pentru orice p impar, dezvoltând în acest fel sumele sau diferențele, observând că, coeficienții termenilor sunt coeficienții care apar din dezvoltarea binomului lui Newton prin formula combinărilor, caz în care ridicând binomul la puterea p, toți termenii se vor divide cu p.
Desigur, demonstrația dată de Geza este mult mai simplă și mai frumoasă, pe care o să-l rog când are timp s-o scrie complet și corect redactată în LaTex, pentru că aceasta ar putea fi formulată ca și lemă într-o eventuală demonstrație, reprezentând un pas important în demonstrație.

Revenim la







de unde rezultă că (x+y), (z-x), (z-y) sunt fie toate numere întregi la puterea p, fie doar una dintre ele îl conține factor pe deoarece cealaltă paranteză îl mai conține pe p factor la puterea întâi, în cazul în care soluția respectivă se divide cu p.

Avem așadar sistemele de soluții :



Din primul sistem putem obține soluțiile :



Din al doilea, același tip de soluții cu diferența că apare în plus factorul lângă , pentru al doilea înmulțit cu și tot așa.

Trebui menționat și faptul că x+y, z-y, z-x sunt prime între ele, deoarece aceste valori sunt factorii lui z, x, y, care nu pot avea factori comuni, ceea ce înseamnă că a, b, c sunt deasemenea prime între ele, nedivizibile cu p, din care unul dintre a, b, c este un număr par.
Ecuația nu admite trei soluții impare, nici toate pare, nici două pare și unul impar, ci doar situația în care două sunt impare, iar unul par, ca și soluții primitive ale ecuației, de un de rezultă de asemenea că una din soluțiile a, b sau c este o soluție pară.

Indiferent dacă în exprimarea uneia din soluții apare sau nu factorul p, vom scrie soluțiile sub forma



și putem aduce ecuația inițială la o ecuație de forma :



situație, care personal, mi se pare un pas înainte în demonstrarea acestui caz.
Voi încerca în continuare să analizez pe rând, cazul p=3,5,7,..să vedem la ce se ajunge plecând de la acest aspect și dacă putem generaliza ceva.
Sugestiile voastre sunt binevenite.

Cred că s-ar putea ajunge la ceva concret demonstrând că dacă u, v sunt prime între ele, iar uu'+vv' se divide cu u+v, atunci u'=v'.
Voi reveni mai târziu cu explicația.
Mai verific o idee concluziile și eventual și o demonstrație pentru concluzia de mai sus.

Apropos, are cineva vreo idee despre cum am putea demonstra că dacă u și v sunt prime între ele, iar  u(u')-v(v') se divide cu u-v, atunci fie u'=v', fie u', v' au un factor comun ?
De asemenea și pentru cazul în care  dacă u(u')+v(v') se divide cu u+v, atunci  fie u'=v', fie u', v' au un factor comun.

curiosul a scris:Apropos, are cineva vreo idee despre cum am putea demonstra că dacă u și v sunt prime între ele, iar  u(u')-v(v') se divide cu u-v, atunci fie u'=v', fie u', v' au un factor comun ?
De asemenea și pentru cazul în care  dacă u(u')+v(v') se divide cu u+v, atunci  fie u'=v',  fie u', v' au un factor comun.

Nu vă mai obosiți să verificați pentru că nu este universal valabil, acestea sunt doar cazuri particulare.
Era minunat să fi fost așa.
Dar...trebuie să găsim altceva.

Plecând de la tot ce este demonstrat în primul mesaj, explicația care demonstrează teorema în acest caz este alta.
Voi relua câteva pasaje din primul mesaj, cu mici modificări.
Așadar,

curiosul a scris:Putrem să scriem pe rând ecuația în trei moduri, deoarece p este prim impar :







În continuare putem demonstra că dezvoltarea celor două diferențe și a sumei prin această metodă, cele două paranteze din dreapta  pot avea ca și factor comun doar p. În cazul diferențelor, demonstrația a fost făcută foarte frumos de Mezei Geza prin teorema împărțirii cu rest a polinoamelor, care poate fi folosită și pentru a demonstra acest lucru în cazul sumei.


De aici putem deduce că (x+y), (z-x), (z-y) sunt fie toate numere întregi la puterea p, fie doar una dintre ele îl conține factor și pe deoarece cealaltă paranteză îl mai conține pe p factor la puterea întâi, în cazul în care soluția respectivă se divide cu p.

Avem așadar, sistemele de soluții :



Din primul sistem putem obține soluțiile :



Din al doilea, același tip de soluții cu diferența că apare în plus factorul înmulțit cu , pentru al treilea înmulțit cu și tot așa.

Trebui menționat și faptul că x+y, z-y, z-x sunt prime între ele, deoarece aceste valori sunt factorii lui z, x, y, soluțiile primitive ale ecuației care nu pot avea factori comuni, ceea ce înseamnă că a, b, c sunt deasemenea prime între ele, nedivizibile cu p, din care unul dintre a, b, c este un număr par.
Ecuația nu admite trei soluții primitive impare, nici toate pare, nici două pare și unul impar, ci doar situația în care două sunt impare, iar unul par,  de unde rezultă de asemenea că una din soluțiile a, b sau c este o soluție pară.

Indiferent dacă în exprimarea uneia din soluții apare sau nu factorul p, în situația în care una din soluțiile x, y, z se divide cu p, vom scrie soluțiile sub forma



și putem aduce ecuația inițială la o ecuație de forma :

Demonstrația se bazează pe faptul că toate soluțiile a', b', c' se divid cu 2, în caz contrar ultima egalitate din citat nu poate fi posibilă.
a', b', c' sunt de fapt soluțiile a, b, c toate la puterea p, sau cazul în care una dintre ele se divide și cu p la puterea pk-1, k natural nenul, dar pentru simplificare, indiferent dacă una dintre ele se divide sau nu și cu p, vom folosi notațiile a', b', c', pentru că nu schimbă concluziile întrucât p este impar și implicit, doar una dintre valorile a', b', c' este un număr par.
Pentru că p este impar, putem scrie ultima egalitate în toate cele trei forme menționate la început, în citat.
În oricare mod am scrie

sau


parantezele mari din dreapta sunt numere impare, indiferent că sunt u, v sunt ambele impare, sau unul par și unul impar, pentru că paranteza respectivă conține un număr impar de termeni.

Dezvoltând asemănător ultima egalitate

și notând pentru simplificare paranteza mare cu 2q+1, ajungem la



În membrul din stânga trebuie să-l avem pe 2 la o putere de p, ceea ce înseamnă că a' se divide cu 2 (mai exact la o putere de p-1, sau pk-1).
Dar putem aduce egalitatea și în celelalte forme, unde va rezulta că





de unde, prin același raționament rezultă că b' se divide și el cu 2.
În mod similar, rezultă că c' trebuie de asemenea să se dividă cu 2, altfel egalitatea nu este posibilă.

Carevasăzică, am ajuns la a arăta, revenind în punctul din care s-a plecat, că (x+y), (z-y), (z-x) se divid toate cu 2, de unde rezultă că și că x, y, z trebuie să fie toate divizibile cu 2.
Dar ecuația trebuie să aibă soluții x, y, z prime între ele.

E vreo greșeală pe undeva ?
Mă bazez pe tine Geza !
Desigur, voi analiza oricare alt răspuns.

Salut !
Nu te grabi cu analiza ca nu se intelege absolut nimic.Atentie la detalii.Incearca sa explici babeste ca pentru tolomaci.Stiind tot rationamentul si toti pasii esti tentat sa sari peste anumite elemente care pentru un cititor din exterior nu sunt cunoscute(aceasi greseala am facut-o si eu cazul TG si nu se mai intelege absolut nimic.Trebuie sa refac tot).Explicand babeste si in amanunt te autoajuti ca iti clarifici si toate nedumeririle.

Pe mine m-ai pierdut de la prima fraza:
"Putrem să scriem pe rând ecuația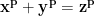 în trei moduri, deoarece p este prim impar"
1-pentru orice p putem scrie relatile respective nu ?
2-nu am inteles ! putem avea p prim si par ? Ce rost are precizarea respectiva in acest context?

La primul punct am gresit eu dar nu am mai putut corecta. Cred ca m-am prins ce ai vrut sa zici si la a doua,oricum fi mai explicit.
Este deja tarziu si nu judec corect.

Domnu Abel.
De ce nu se poate corecta un mesaj si dupa 1000 de ani dupa ce a fost scris ? Sau chiar sterge daca autorul considera ca este o eroare sau pur si simplu si-a schimbat punctul de vedere.
Sa fiu rau te intreb:Se incearca a se face o colectie de "perle" ?

Și în ultimul mesaj e o greșeală.
Deși într-adevăr, a', b', c', sunt două impare și unul par, suma lor, diferența lor sau orice combinație de sumă sau diferență între ele va fi un număr par, situație în care paranteza aceea mare se va divide cu 2, chiar cu 2 la puterea p-1 (sau la pk-1).
Și ai dreptate, trebuie scris pas cu pas, băbește, cum zici tu.
Mai ales că nu mulți au răbdare să stea să deducă ceea ce nu reiese evident.
Voi reveni cu un mesaj, dar în celălalt topic pentru cazul n=4, păstrând același raționament, scriindu-l însă complet, pas cu pas.