Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Meteorr Ieri la 21:34
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Joi 21 Noi 2024, 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la CAdi în Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
( 1 )
» Mesaj de la CAdi în OZN in Romania
( 1 )
» Mesaj de la virgil în Carti sau documente de care avem nevoie
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| Dacu2 | ||||
| eugen | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Abel Cavaşi |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| virgil | ||||
| Dacu2 | ||||
| CAdi | ||||
| Meteorr | ||||
| ilasus | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 30 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 30 Vizitatori :: 1 Motor de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Cazul n=4 al Teoremei lui Fermat
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 1 din 1
 Cazul n=4 al Teoremei lui Fermat
Cazul n=4 al Teoremei lui Fermat
Mi-am permis să deschid un subiect separat plecând de la ultimele 3 mesaje din alt topic pentru că o analiză mai amănunțită ar putea demonstra cazul particular al acestei teoreme.
Mă bazez, în limita timpului său disponibil, pe părerile și observațiile lui Geza, pentru care îi mulțumesc.
În subiectul respectiv
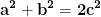 , a, b, c impare, prime între ele.
, a, b, c impare, prime între ele.
Am analizat pentru început situația în care una din valorile a sau b este 1.
Am dat, cel puțin în partea de început a soluțiilor consecutive peste o constantă, într-un fel sau altul.
Iată prime valori numerice care respectă condițiile :
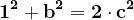
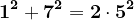
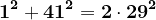

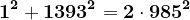
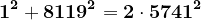
...
Dacă am nota valorile 7, 41, 239, 1393, 8119,...cu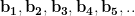 observăm că relația de recurență este
observăm că relația de recurență este 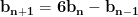 , iar în mod similar pentru c,
, iar în mod similar pentru c,  .
.
Întrebarea mea acum este dacă în acest caz, pentru a=1, toate soluțiile ecuației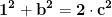 pot fi obținute prin relația de recurență de mai sus.
pot fi obținute prin relația de recurență de mai sus.
Deocamdată doar am calculat, fără să încerc să stabilesc prin ecuații algebrice dacă rezultă acest lucru.
Cum am spus, pentru moment voi face doar calcule numerice, pentru a verifica constantele care apar, urmând să încerc să generalizez o exprimare prin care se pot găsi soluțiile ecuației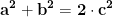 pentru a, b, c impare, prime între ele.
pentru a, b, c impare, prime între ele.
Dacă ai timp, orice părere mi-ar fi utilă, iar în continuare voi încerca să găsesc constante între soluțiile ecuației pentru a=3,5,7,9..., încercând ulterior să observ dacă există și dacă poate fi formulată o relație de recurență generală.
Mă bazez, în limita timpului său disponibil, pe părerile și observațiile lui Geza, pentru care îi mulțumesc.
În subiectul respectiv
șicuriosul a scris:Ecuațiaare alte soluții cu excepția soluțiilor
?
Dacă da, pot fi generalizate soluțiile întregi ale acestei ecuații după o anumită exprimare generală a lor ?
Geza, am luat-o băbește, prin calcul numeric, încercând ca apoi, pe baza constantelor pe care le pot observa să încerc să generalizez o modalitate de exprimare a soluțiilor ecuațieicuriosul a scris:OK, mersi Geza.
Întrebarea a apărut analizândși aducând egalitatea la forma unei ecuații pitagorice
, unde
,
,
cu soluțiile
cu u, v impare prime între ele.
Am analizat pentru început situația în care una din valorile a sau b este 1.
Am dat, cel puțin în partea de început a soluțiilor consecutive peste o constantă, într-un fel sau altul.
Iată prime valori numerice care respectă condițiile :
...
Dacă am nota valorile 7, 41, 239, 1393, 8119,...cu
Întrebarea mea acum este dacă în acest caz, pentru a=1, toate soluțiile ecuației
Deocamdată doar am calculat, fără să încerc să stabilesc prin ecuații algebrice dacă rezultă acest lucru.
Cum am spus, pentru moment voi face doar calcule numerice, pentru a verifica constantele care apar, urmând să încerc să generalizez o exprimare prin care se pot găsi soluțiile ecuației
Dacă ai timp, orice părere mi-ar fi utilă, iar în continuare voi încerca să găsesc constante între soluțiile ecuației pentru a=3,5,7,9..., încercând ulterior să observ dacă există și dacă poate fi formulată o relație de recurență generală.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cazul n=4 al Teoremei lui Fermat
Re: Cazul n=4 al Teoremei lui Fermat
Geza, se pare că dacă valorile a, b, c sunt toate mai mari ca 1, ca și soluții ale ecuației 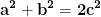 , atunci ele au un factor comun.
, atunci ele au un factor comun.
Dacă una dintre valorile a sau b este egală cu 1, a să spunem, ecuația are soluții prime între ele, impare, așa cum rezultă de mai sus.
Dacă a este mai mare ca 1, soluțiile ecuației sunt soluțiile pentru a=1 înmulțite toate cu un număr impar.
Spre exemplu, dacă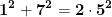 , atunci
, atunci ^2=2\cdot&space;(3\cdot&space;5)^2}) , precum și pentru toate celelalte cazuri.
, precum și pentru toate celelalte cazuri.
Evident prin simplificarea ecuației cu factorul comun impar respectiv la puterea 2.
Dacă a, b, c sunt mai mari ca 1, atunci ecuația nu admite soluții a, b, c impare, toate prime între ele.
Rămâne să demonstrăm asta.
Prin calcul numeric se verifică, cel puțin pentru valorile pe care le-am încercat, dar trebuie o demonstrație.
Dacă una dintre valorile a sau b este egală cu 1, a să spunem, ecuația are soluții prime între ele, impare, așa cum rezultă de mai sus.
Dacă a este mai mare ca 1, soluțiile ecuației sunt soluțiile pentru a=1 înmulțite toate cu un număr impar.
Spre exemplu, dacă
Evident prin simplificarea ecuației cu factorul comun impar respectiv la puterea 2.
Dacă a, b, c sunt mai mari ca 1, atunci ecuația nu admite soluții a, b, c impare, toate prime între ele.
Rămâne să demonstrăm asta.
Prin calcul numeric se verifică, cel puțin pentru valorile pe care le-am încercat, dar trebuie o demonstrație.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Re: Cazul n=4 al Teoremei lui Fermat
Re: Cazul n=4 al Teoremei lui Fermat
Să-ți arăt, Geza, pentru început, cea mai simplă demonstrație a faptului că soluțiile întregi ale ecuației 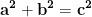 trebuie să poată fi exprimate
trebuie să poată fi exprimate
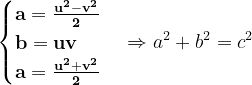
Ecuația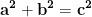 admite soluții întregi prime între ele. Una din soluțiile a sau b este o soluție impară, altfel, dacă ambele ar fi pare, atunci c ar fi de asemenea o soluție pară, iar ecuația nu ar avea soluții prime întyre ele, caz în care toate s-ar divide cu 2. Deci una din soluțiile a sau b este un întreg impar. Fie b soluția impară.
admite soluții întregi prime între ele. Una din soluțiile a sau b este o soluție impară, altfel, dacă ambele ar fi pare, atunci c ar fi de asemenea o soluție pară, iar ecuația nu ar avea soluții prime întyre ele, caz în care toate s-ar divide cu 2. Deci una din soluțiile a sau b este un întreg impar. Fie b soluția impară.
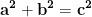
(c+a)}) , unde c si a au paritate diferită, în același timp nefiind divizibile de un număr prim impar, de unde rezultă că atât c-a, cât și c+a sunt prime între ele, iar din egalitatea
, unde c si a au paritate diferită, în același timp nefiind divizibile de un număr prim impar, de unde rezultă că atât c-a, cât și c+a sunt prime între ele, iar din egalitatea (c+a)}) rezultă că ambele sunt pătrate perfecte.
rezultă că ambele sunt pătrate perfecte.
Fie b=uv, ceea ce înseamnă că=v^2}) , iar
, iar =u^2}) .
.
Atunci+(c+a)=u^2+v^2}) , deci
, deci 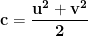 , iar
, iar -(c-a)=u^2-v^2}) unde
unde 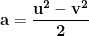 .
.
Deci soluțiile a, b, c primitive ale ecuației trebuie obligatoriu să poată fi exprimate în acest fel.
În cazul ecuației^2+(y^2)^2=(z^2)^2}) , cum rezultă de mai sus, avem soluțiile pentru y impar :
, cum rezultă de mai sus, avem soluțiile pentru y impar :
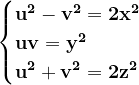
cu uv impare prime între ele.
Dacă, am presupune că observațiile mele din mesajele mele sunt adevărate, iar ecuația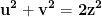 nu admite soluții u, v, z impare prime între ele, mai mari ca 1, ci doar cazul în care una din valorile u sau v este egal cu 1, atunci din a doua relație a sistemului rezultă că
nu admite soluții u, v, z impare prime între ele, mai mari ca 1, ci doar cazul în care una din valorile u sau v este egal cu 1, atunci din a doua relație a sistemului rezultă că  și înlocuind în prima relație a sistemului ar rezulta că
și înlocuind în prima relație a sistemului ar rezulta că
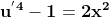
({u}^{'2}+1)=2x^2}) , unde cele două paranteze sunt două numere pare consecutive, singurul lor factor comun putând fi doar 2.
, unde cele două paranteze sunt două numere pare consecutive, singurul lor factor comun putând fi doar 2.
Putem demonstra că z este obligatoriu impar pentru soluțiile x, y, z ca fiind soluții primitive ale ecuației^2+(y^2)^2=(z^2)^2}) , aducând ecuația la forma
, aducând ecuația la forma
(x^2+y^2+z^2)=2x^2y^2}) , unde dacă am presupune că x și y sunt impare, atunci membrul din stânga se divide cu 4 în timp ce acela din dreapta doar cu 2.
, unde dacă am presupune că x și y sunt impare, atunci membrul din stânga se divide cu 4 în timp ce acela din dreapta doar cu 2.
Deci dacă y este impar atunci x este par și notăm(({u}^{'2}+1)=2(2^n{x}'{x}'')^2}) , iar dacă singurul factor comun al celor două paranteze din stânga este doi, una dintre ele va fi
, iar dacă singurul factor comun al celor două paranteze din stânga este doi, una dintre ele va fi =2{x}''^2}) , iar cealaltă va fi
, iar cealaltă va fi =2^{2n}{x}'^2}) , sau invers.
, sau invers.
Pentru oricare situație, una din valorile}) sau
sau }) va fi un pătrat perfect, situație imposibilă în ambele cazuri.
va fi un pătrat perfect, situație imposibilă în ambele cazuri.
Cu alte cuvinte, nu există întregi s, t astfel încât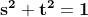 , sau
, sau 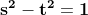 .
.
Deci trebuie demonstrat că ecuația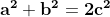 nu are soluții a, b, c impare, prime între ele, toate mai mari ca 1, ci doar cazul în care una din soluțiile a sau b este egală cu 1.
nu are soluții a, b, c impare, prime între ele, toate mai mari ca 1, ci doar cazul în care una din soluțiile a sau b este egală cu 1.
Ecuația
Fie b=uv, ceea ce înseamnă că
Atunci
Deci soluțiile a, b, c primitive ale ecuației trebuie obligatoriu să poată fi exprimate în acest fel.
În cazul ecuației
cu uv impare prime între ele.
Dacă, am presupune că observațiile mele din mesajele mele sunt adevărate, iar ecuația
Putem demonstra că z este obligatoriu impar pentru soluțiile x, y, z ca fiind soluții primitive ale ecuației
Deci dacă y este impar atunci x este par și notăm
Pentru oricare situație, una din valorile
Cu alte cuvinte, nu există întregi s, t astfel încât
Deci trebuie demonstrat că ecuația
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41554
Data de inscriere : 22/03/2011
 Subiecte similare
Subiecte similare» Cazul n=p, p prim impar al teoremei lui Fermat
» Marea teorema a lui Fermat.
» Mica teoremă a lui Fermat
» Marea teorema a lui Fermat.
» Mica teoremă a lui Fermat
Forum pentru cercetare :: Cercetări în Matematică :: Aritmetica şi Teoria numerelor :: Teoremele lui Fermat
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 