Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Forever_Man Ieri la 22:56
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la Razvan în Global warming is happening?
( 1 )
» Mesaj de la Abel Cavaşi în ChatGPT este din ce în ce mai receptiv
( 1 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12458) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Spune şi altora
Cine este conectat?
În total sunt 32 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 32 Vizitatori Nici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
2 participanți
Pagina 1 din 1
 Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Ştim că, dată fiind o traiectorie oarecare netedă şi continuă, putem defini un triedru drept format cu versorii tangentă (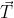 ), normală (
), normală (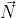 ) şi binormală (
) şi binormală (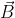 ), care triedru să satisfacă următoarele formule, stabilite de Frenet:
), care triedru să satisfacă următoarele formule, stabilite de Frenet:
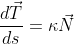 ,
,
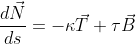 ,
,
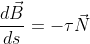 ,
,
unde şi
şi 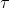 sunt curbura şi, respectiv, torsiunea traiectoriei date.
sunt curbura şi, respectiv, torsiunea traiectoriei date.
Să arătăm acum că, alături de triedrul lui Frenet asociat unei traiectorii, mai putem construi un alt triedru special asociat traiectoriei date, format tot cu versorii triedrului lui Frenet, astfel încât şi noul triedru să satisfacă formulele lui Frenet.
Pentru aceasta, vom demonstra următoarea
Teoremă:
Triedrul drept format cu versorii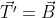 ,
, 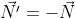 şi
şi 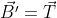 satisface şi el formulele lui Frenet corespunzătoare
satisface şi el formulele lui Frenet corespunzătoare
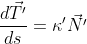 ,
,
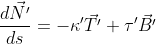 ,
,
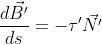 ,
,
unde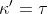 şi
şi 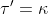 .
.
Demonstraţie.
Făcând înlocuirile necesare şi folosindu-ne de formulele lui Frenet asociate triedrului (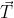 ,
, 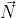 ,
, 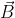 ), obţinem
), obţinem
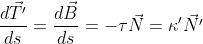 ,
,
=\kappa\vec{T}-\tau\vec{B}=-\kappa'\vec{T'}+\tau'\vec{B'}) ,
,
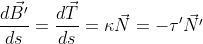 ,
,
ceea ce trebuia demonstrat.
Definiţia 1. Numim triedru ortogonal al lui Frenet, triedrul (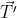 ,
, 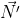 ,
, 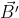 ) .
) .
Definiţia 2. Numim traiectorie ortogonală, acea traiectorie care ar fi parcursă de un mobil aflat în originea triedrului ortogonal al lui Frenet.
Să vă fie cu folos!
unde
Să arătăm acum că, alături de triedrul lui Frenet asociat unei traiectorii, mai putem construi un alt triedru special asociat traiectoriei date, format tot cu versorii triedrului lui Frenet, astfel încât şi noul triedru să satisfacă formulele lui Frenet.
Pentru aceasta, vom demonstra următoarea
Teoremă:
Triedrul drept format cu versorii
unde
Demonstraţie.
Făcând înlocuirile necesare şi folosindu-ne de formulele lui Frenet asociate triedrului (
ceea ce trebuia demonstrat.
Definiţia 1. Numim triedru ortogonal al lui Frenet, triedrul (
Definiţia 2. Numim traiectorie ortogonală, acea traiectorie care ar fi parcursă de un mobil aflat în originea triedrului ortogonal al lui Frenet.
Să vă fie cu folos!
 Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Mult mai simplu, dar de unde-ți rezultă:
Abel Cavaşi a scris:
undeşi
.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Da, din modul în care sunt exprimate formulele precedente, inițiale.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Și totuși, de unde-ți rezultă:
Abel Cavaşi a scris:
undeşi
.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Făcând această alegere, putem demonstra teorema. Altfel spus, aceste relaţii nu „rezultă” din altele, ci ele implică demonstraţia teoremei. Ele nu sunt un efect, ci o cauză.curiosul a scris:Și totuși, de unde-ți rezultă:Abel Cavaşi a scris:
undeşi
.
 Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Abel, din punct de vedere logic și ținând cont de ce ai afirmat :
În linii mari, dacă identitățile
Plecând de la triedrul inițial format cu versorii tangentă (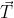 ), normală (
), normală (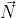 ) şi binormală (
) şi binormală (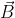 ), care satisface următoarele formule, stabilite de Frenet:
), care satisface următoarele formule, stabilite de Frenet:
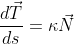 ,
,
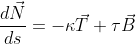 ,
,
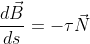 ,
,
putem construi triedrul drept format cu versorii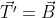 ,
, 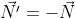 şi
şi 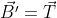 .
.
Acesta din urmă satisface la rândul lui formulele lui Frenet (și acum apare cauza), dacă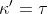 şi
şi 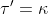 .
.
După cum vezi, am evidențiat dacă.
În această situație, concluzia, implicația este adevărată dacă identitățile cauzei implicării sunt adevărate.
Deci satisfacerea formulelor lui Frenet pentru triedrul ortogonal depinde de aceea cauză,
iar valoarea de adevăr a concluziei este determinată de valoarea de adevăr a ipotezei presupuse, a cauzei.
Cauza adevărată, concluzie adevărată ; cauza falsă - concluzia falsă.
Deci trebuie stabilită valoarea de adevăr a cauzei.
această afirmație schimbă raționamentul demonstrației.Abel Cavaşi a scris:Făcând această alegere, putem demonstra teorema. Altfel spus, aceste relaţii nu „rezultă” din altele, ci ele implică demonstraţia teoremei. Ele nu sunt un efect, ci o cauză.
În linii mari, dacă identitățile
nu sunt demonstrate, ele reprezentând o cauză, atunci din analiza primei postări rezultă că :Abel Cavaşi a scris:
şi
.
Plecând de la triedrul inițial format cu versorii tangentă (
putem construi triedrul drept format cu versorii
Acesta din urmă satisface la rândul lui formulele lui Frenet (și acum apare cauza), dacă
După cum vezi, am evidențiat dacă.
În această situație, concluzia, implicația este adevărată dacă identitățile cauzei implicării sunt adevărate.
Deci satisfacerea formulelor lui Frenet pentru triedrul ortogonal depinde de aceea cauză,
iar valoarea de adevăr a concluziei este determinată de valoarea de adevăr a ipotezei presupuse, a cauzei.
Cauza adevărată, concluzie adevărată ; cauza falsă - concluzia falsă.
Deci trebuie stabilită valoarea de adevăr a cauzei.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Sau altfel, schimbând ordinea de implicare parametrizând-o prin logica
DACĂ -> ATUNCI
putem verifica corectitudinea implicării în alt mod.
DACĂ atât triedrul inițial, cât și triedrul ortogonal satisfac formulele lui Frenet, ATUNCI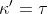 şi
şi 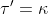 .
.
În funcție de ce vrei să demonstrezi, stabilești cauza DACĂ și concluzia ATUNCI.
În oricare situație, cauza trebuie să fie adevărată ca să implice concluzia.
DACĂ -> ATUNCI
putem verifica corectitudinea implicării în alt mod.
DACĂ atât triedrul inițial, cât și triedrul ortogonal satisfac formulele lui Frenet, ATUNCI
În funcție de ce vrei să demonstrezi, stabilești cauza DACĂ și concluzia ATUNCI.
În oricare situație, cauza trebuie să fie adevărată ca să implice concluzia.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Păi, în orice teoremă este valabil acest lucru. Nu se pune problema falsității premiselor, ci se pune problema aplicabilității teoremei respective.
 Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Dacă premisele sunt false, sau nedemonstrate, atunci demonstrația nu este corectă sau completă, ceea ce face ca aplicabilitatea teoremei să fie cel puțin discutabilă din punctul meu de vedere.
Dar o să-i las pe alții mai experimentați să-și spună părerea.
Dar o să-i las pe alții mai experimentați să-și spună părerea.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Propoziția "Dacă P atunci Q" poate fi adevărată chiar dacă P este falsă.
 Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Foarte adevărat !Abel Cavaşi a scris:Propoziția "Dacă P atunci Q" poate fi adevărată chiar dacă P este falsă.
Propoziția "Dacă P atunci Q", în esența ei ca și propoziție este adevărată indiferent de valoarea de adevăr a lui P.
Însă propoziția, nu implicarea Q.
Dacă P este fals, Q este fals, atât timp cât Q este implicată de P fals, iar cel puțin în ce privește teorema ta P trebuie să fie adevărat.
Ori tu consideri că ai demonstrat că Q este adevărat.
Din păcate, din punctul meu de vedere nu rezultă.
Dar cine știe, s-ar putea să mă înșel, deși mă îndoiesc.
Chiar dacă părerile mele deranjează, îți sunt mai utile decât o susținere fără rost.
Eu știu că ai muncit mult cu teorema asta și ți-ai făcut multe speranțe, dar s-ar putea să nu fie chiar așa cum susții.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
De fapt nu, chiar ai dreptate.
Din propoziția dacă P, atunci Q, Q poate fi adevărat chiar dacă P este fals.
Scuze că m-am răzvrătit așa.
Dar în cazul demonstrației tale P trebuie să fie adevărat, pentru că implică direct și în același fel valoarea de adevăr a lui Q, dar trebuie să găsești valoarea de adevăr a lui P, ca să stabilești valoarea de adevăr a lui Q.
Ori tu ai considerat ca fiind adevărată din start.
De unde rezultă ?
Din propoziția dacă P, atunci Q, Q poate fi adevărat chiar dacă P este fals.
Scuze că m-am răzvrătit așa.
Dar în cazul demonstrației tale P trebuie să fie adevărat, pentru că implică direct și în același fel valoarea de adevăr a lui Q, dar trebuie să găsești valoarea de adevăr a lui P, ca să stabilești valoarea de adevăr a lui Q.
Ori tu ai considerat ca fiind adevărată din start.
De unde rezultă ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
P este adevărată deoarece formulele lui Frenet sunt adevărate. Restul au fost doar înlocuiri.
 Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Re: Triedrul ortogonal al lui Frenet şi traiectoria ortogonală
Dacă 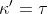 şi
şi 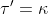 asta ar însemna că torsiunea triedrului 1 este curbura triedrului 2 și curbura triedrului 1 este torsiunea triedrului 2, nu ?
asta ar însemna că torsiunea triedrului 1 este curbura triedrului 2 și curbura triedrului 1 este torsiunea triedrului 2, nu ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Subiecte similare
Subiecte similare» Legi de conservare (2)
» Orice vector are un triedru Frenet
» Traiectoria unui corp este reala sau virtuala?
» Orice vector are un triedru Frenet
» Traiectoria unui corp este reala sau virtuala?
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 
