Ultimele subiecte
» Dovezi ce atestă existența lui DUMNEZEU și că EL este UNICUL CREATOR al UniversuluiScris de CAdi Astazi la 12:25
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de CAdi Astazi la 12:13
» Ce anume "generează" legile fizice?
Scris de CAdi Astazi la 12:07
» În ce tip de dovezi aveţi încredere deplină?
Scris de Forever_Man Ieri la 21:41
» Unde a ajuns stiinta ?
Scris de virgil Ieri la 18:02
» Ce fel de popor suntem
Scris de virgil Ieri la 17:40
» Eu sunt Dumnezeu - viitoarea mea carte in limba romana
Scris de Forever_Man Dum 24 Noi 2024, 09:16
» ChatGPT este din ce în ce mai receptiv
Scris de Meteorr Sam 23 Noi 2024, 21:12
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 1 )
» Mesaj de la virgil în Ce anume "generează" legile fizice?
( 1 )
» Mesaj de la CAdi în ChatGPT este din ce în ce mai receptiv
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12466) | ||||
| CAdi (12403) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7964) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3970) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Dacu2 | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 12 utilizatori conectați: 1 Înregistrați, 0 Invizibil și 11 Vizitatori :: 2 Motoare de căutareDacu2
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Are cineva vreo idee ?
2 participanți
Pagina 1 din 1
 Are cineva vreo idee ?
Are cineva vreo idee ?
Fie  un oarecare număr prim impar și un număr prim
un oarecare număr prim impar și un număr prim ) .
.
S-ar putea demonstra că pentru orice număr par 2k , există cel puțin un număr prim P, , astfel încât P+2k nu se divide cu niciun număr prim mai mic sau egal cu
, astfel încât P+2k nu se divide cu niciun număr prim mai mic sau egal cu  ?
?
Orakle, ai vreo idee de pornire măcar ?
Sau oricine altcineva ?
S-ar putea demonstra că pentru orice număr par 2k , există cel puțin un număr prim P,
Orakle, ai vreo idee de pornire măcar ?
Sau oricine altcineva ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
Orakle, dacă se poate generalizat demonstra asta, am împușcat cel puțin trei iepuri dintr-un foc.
În funcție de cum mai ricoșează glonțul, poate mai nimeresc vreun iepure.
Eu am analizat-o pentru început așa.
Am considerat că orice număr par 2k l-am putea scrie sub forma

Pentru v=0, orice P+2k, , este un număr care nu se divide cu niciun număr prim mai mic sau egal cu
, este un număr care nu se divide cu niciun număr prim mai mic sau egal cu  .
.
Spre exemplu, pentru v=k, este suficient să existe o pereche de numere prime între care există o diferență de 2k,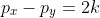 ,
,  ca afirmația să fie adevărată.
ca afirmația să fie adevărată.
Situația devine ceva mai complicată când v are o valoare nenulă ce nu respectă condițiile de mai sus și este nevoie de generalizarea situației.
Ai vreo idee ?
În funcție de cum mai ricoșează glonțul, poate mai nimeresc vreun iepure.
Eu am analizat-o pentru început așa.
Am considerat că orice număr par 2k l-am putea scrie sub forma
Pentru v=0, orice P+2k,
Spre exemplu, pentru v=k, este suficient să existe o pereche de numere prime între care există o diferență de 2k,
Situația devine ceva mai complicată când v are o valoare nenulă ce nu respectă condițiile de mai sus și este nevoie de generalizarea situației.
Ai vreo idee ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
curiosul a scris:Orakle, dacă se poate generalizat demonstra asta, am împușcat cel puțin trei iepuri dintr-un foc.
În funcție de cum mai ricoșează glonțul, poate mai nimeresc vreun iepure.
Primul iepure, și cel mai important pentru mine, este conjectura lui Goldbach.
Dacă s-ar putea demonstra că :
prin condițiacuriosul a scris: pentru orice număr par 2k , există cel puțin un număr prim P,, astfel încât P+2k nu se divide cu niciun număr prim mai mic sau egal cu

rezultă că există P astfel încât
unde
Aceasta este adevărat doar dacă 2m-P este un număr care nu se divide cu niciun număr prim mai mic sau egal cu
Înțelegi ce vreau să spun ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
Deci, cu alte cuvinte, putem reduce demonstrația enunțului conjecturii lui Goldbach, la a demonstra că există un număr prim impar P,  , astfel încât P+2k nu se divide cu niciun număr prim mai mic sau egal cu
, astfel încât P+2k nu se divide cu niciun număr prim mai mic sau egal cu  , pentru orice k natural.
, pentru orice k natural.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
Cred că enunțul de mai sus se poate demonstra.
Dacă raționamentul pe care l-am folosit nu are nicio greșeală, sper să pot scrie demonstrația diseară.
Îl mai analizez un pic, poate îmi scapă ceva ce nu am luat în calcul.
Dacă raționamentul pe care l-am folosit nu are nicio greșeală, sper să pot scrie demonstrația diseară.
Îl mai analizez un pic, poate îmi scapă ceva ce nu am luat în calcul.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
Păi meteor, se pare că Chen n-a demonstrat că orice număr par este diferența a două numere prime, ci aceasta este încă o întrebare deschisă, din câte am citit pe net.
Există cumva vreo demonstrație a faptului că orice număr par este diferența a două numere prime ?
Pentru că ceea ce am afirmat mai sus :
Tu tot vorbești de Chen și Vinogradov, dar ai acces la acele demonstrații ?
Dacă da, mi le poți trimite și mie ?
Sau vorbești doar din ce ai citit și tu pe net ?
Există cumva vreo demonstrație a faptului că orice număr par este diferența a două numere prime ?
Pentru că ceea ce am afirmat mai sus :
se poate demonstra dacă există o demonstrație a faptului că orice număr par este diferența a două numere prime.curiosul a scris: există un număr prim impar P,, astfel încât P+2k nu se divide cu niciun număr prim mai mic sau egal cu
, pentru orice k natural nenul.
Tu tot vorbești de Chen și Vinogradov, dar ai acces la acele demonstrații ?
Dacă da, mi le poți trimite și mie ?
Sau vorbești doar din ce ai citit și tu pe net ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
Nu am raspuns ca am fost ocupat.
Nu pricep mimic din acele demonstration, CEA a lui Vinogradov am gasit chindva ceva pe niste siteuri rusesti. Din chute am inteles, idea AIA a sa sau a lui Levin, she socot originale.
Nu pricep mimic din acele demonstration, CEA a lui Vinogradov am gasit chindva ceva pe niste siteuri rusesti. Din chute am inteles, idea AIA a sa sau a lui Levin, she socot originale.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25855
Data de inscriere : 19/06/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
OK meteor.
Deci mai am un pic.
Dar nu mă las până nu-i dau de capăt.
Deci mai am un pic.
Dar nu mă las până nu-i dau de capăt.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
Orakle, am nevoie să mă ajuți la ceva.
Trebuie să demonstrez că dacă rația unei progresii aritmetice de P(n)-1 termeni nu se divide cu P(n), atunci există un termen al progresiei care se divide cu P(n).
Ca să înțelegi mai bine, îți dau un exemplu.
Să luăm numărul prim P(n)=11, spre exemplu, și alegem o rație nedivizibilă cu 11, să zicem 18.
Atunci oricare ar fi a, unul din termenii
a, a+18, a+2*18, a+3*18,...a+10*18
se divide cu P(n).
Pentru a=2 spre exemplu, 2+6*18=110 este divizibil cu 11.
Pentru a=23 spre exemplu, 23+3*18=77 este divizibil cu 11.
Și așa mai departe, indiferent de ce rație nedivizibilă cu P(n) folosim.
Evident, dacă primul termen este divizibil cu p(n) enunțul se verifică, deci ar trebui calculat pentru rația și primul termen nedivizibili cu P(n), ai unei progresii aritmetice de P(n)-1 termeni.
Înțelegi ce vreau să spun ?
N-ar fi greu, dar m-am cam obosit astăzi și nu mai am idei.
Dacă se demonstrează asta, am găsit un raționament care demonstrează o serie de alte ipoteze.
Deci ai vreo idee despre cum am putea demonstra că dacă rația unei progresii aritmetice de P(n)-1 termeni nu se divide cu P(n), atunci există un termen al progresiei care se divide cu P(n) ?
Mulțumesc mult !
Trebuie să demonstrez că dacă rația unei progresii aritmetice de P(n)-1 termeni nu se divide cu P(n), atunci există un termen al progresiei care se divide cu P(n).
Ca să înțelegi mai bine, îți dau un exemplu.
Să luăm numărul prim P(n)=11, spre exemplu, și alegem o rație nedivizibilă cu 11, să zicem 18.
Atunci oricare ar fi a, unul din termenii
a, a+18, a+2*18, a+3*18,...a+10*18
se divide cu P(n).
Pentru a=2 spre exemplu, 2+6*18=110 este divizibil cu 11.
Pentru a=23 spre exemplu, 23+3*18=77 este divizibil cu 11.
Și așa mai departe, indiferent de ce rație nedivizibilă cu P(n) folosim.
Evident, dacă primul termen este divizibil cu p(n) enunțul se verifică, deci ar trebui calculat pentru rația și primul termen nedivizibili cu P(n), ai unei progresii aritmetice de P(n)-1 termeni.
Înțelegi ce vreau să spun ?
N-ar fi greu, dar m-am cam obosit astăzi și nu mai am idei.
Dacă se demonstrează asta, am găsit un raționament care demonstrează o serie de alte ipoteze.
Deci ai vreo idee despre cum am putea demonstra că dacă rația unei progresii aritmetice de P(n)-1 termeni nu se divide cu P(n), atunci există un termen al progresiei care se divide cu P(n) ?
Mulțumesc mult !
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
curiosul a scris:Orakle, am nevoie să mă ajuți la ceva.
Trebuie să demonstrez că dacă rația unei progresii aritmetice de P(n)-1 termeni nu se divide cu P(n), atunci există un termen al progresiei care se divide cu P(n).
Ar ajuta cu ceva faptul că 1+2+3+4+...+ P(n)-1 este divizibil cu P(n) ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
Gata Orakle, i-am dat de capăt !
Urrra !
În mare, principiul demonstrației se bazează pe faptul că la un moment dat, se ajunge ca diferența a două numere care au același rest prin împărțirea la p, nu este un număr divizibil cu p.
Există un raționament prin care se ajunge la asta.
Este foarte interesantă modalitatea prin care se poate demonstra enunțul :
Nu știu dacă am timp să redactez astăzi, dar să urmărești mâine topicul și să-mi spui te rog părerea ta.
Asta demonstrează o grămadă de lucruri, printre care, și cele mai importante, conjectura lui Goldbach și infinitatea numerelor prime gemene.
Poate totuși am timp astăzi.
Urrra !
În mare, principiul demonstrației se bazează pe faptul că la un moment dat, se ajunge ca diferența a două numere care au același rest prin împărțirea la p, nu este un număr divizibil cu p.
Există un raționament prin care se ajunge la asta.
Este foarte interesantă modalitatea prin care se poate demonstra enunțul :
curiosul a scris: există un număr prim impar P,, astfel încât P+2k nu se divide cu niciun număr prim mai mic sau egal cu
, pentru orice k natural nenul.
Nu știu dacă am timp să redactez astăzi, dar să urmărești mâine topicul și să-mi spui te rog părerea ta.
Asta demonstrează o grămadă de lucruri, printre care, și cele mai importante, conjectura lui Goldbach și infinitatea numerelor prime gemene.
Poate totuși am timp astăzi.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
Deci...să vedem !
Pentru orice număr par 2k există un număr prim P, , astfel încât P+2k este un număr care nu se divide cu niciun număr prim mai mic sau egal cu
, astfel încât P+2k este un număr care nu se divide cu niciun număr prim mai mic sau egal cu 
Putem verifica afirmația pentru primele câteva numere prime .
.
Dacă vom considera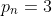 observăm că orice număr par este diferența dintre un număr impar care nu se divide cu 3 și unul din numerele prime 3, 5 sau 7, acestea din urmă fiind numerele prime impare mai mici ca pătratul lui 3.
observăm că orice număr par este diferența dintre un număr impar care nu se divide cu 3 și unul din numerele prime 3, 5 sau 7, acestea din urmă fiind numerele prime impare mai mici ca pătratul lui 3.
2=7-5
4=11-7=7-3
...
20=23-3=25-5
Am dat exemplul cu 5+20 =25 pentru că trebuie să fie vorba de un număr impar nedivizibil cu 2 sau 3, nu neapărat prim, așa cum cere și enunțul.
Deci observăm că pentru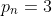 , există un număr prim P, mai mic ca
, există un număr prim P, mai mic ca  astfel încât oricare ar fi un număr par 2k, P+2k este un număr care nu se divide cu 2 și 3.
astfel încât oricare ar fi un număr par 2k, P+2k este un număr care nu se divide cu 2 și 3.
La fel de bine, afirmația se verifică ușor prin calcul și pentru numerele prime .
.
Voi încerca să demonstrez prin inducție, considerând că dacă oricare ar fi numărul par 2k și există un număr prim , atunci există
, atunci există  astfel încât oricare ar fi numărul par 2k, P+2k este un număr care nu se divide cu niciun număr prim mai mic sau egal cu
astfel încât oricare ar fi numărul par 2k, P+2k este un număr care nu se divide cu niciun număr prim mai mic sau egal cu  .
.
Considerăm un număr par oarecare 2k.
Acest număr par îl putem scrie ca fiind
Știm că există un număr prim astfel încât
astfel încât  nu este divizibil cu niciun număr prim mai mic sau egal cu
nu este divizibil cu niciun număr prim mai mic sau egal cu 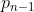 , însă acesta s-ar putea divide cu
, însă acesta s-ar putea divide cu  .
.
Dacă numărul nu se divide cu niciun număr prim mai mic sau egal cu
nu se divide cu niciun număr prim mai mic sau egal cu 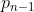 atunci înseamnă p-2m nu se divide cu niciun număr prim mai mic sau egal cu
atunci înseamnă p-2m nu se divide cu niciun număr prim mai mic sau egal cu 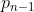 . Altfel, dacă s-ar divide, s-ar putea scoate factor comun acel număr prim mai mic sau egal cu
. Altfel, dacă s-ar divide, s-ar putea scoate factor comun acel număr prim mai mic sau egal cu 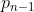 , iar numărul
, iar numărul  nu se divide cu niciun număr prim mai mic sau egal cu
nu se divide cu niciun număr prim mai mic sau egal cu 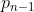 .
.
Putem scrie numărul în mai multe moduri :
în mai multe moduri :

+\left&space;(&space;p_n-1&space;\right&space;)\prod_{i=1}^{n-1}p_i&space;=)
+\left&space;(&space;p_n-2&space;\right&space;)\prod_{i=1}^{n-1}p_i&space;=)
+\left&space;(&space;p_n-3&space;\right&space;)\prod_{i=1}^{n-1}p_i&space;=)
...
\cdot&space;\prod_{i=1}^{n-1}p_i-&space;2m&space;\right&space;)+k\prod_{i=1}^{n-1}p_i)
unde![k\in \left [ 1,\left ( p_n-1 \right ) \right ]](http://latex.codecogs.com/gif.latex?\dpi{110}&space;k\in&space;\left&space;[&space;1,\left&space;(&space;p_n-1&space;\right&space;)&space;\right&space;])
Dacă oricare din termenii scriși în parantezele din stânga ai seriei de mai sus este un număr care se divide cu , atunci numărul
, atunci numărul  nu se divide cu nici cu
nu se divide cu nici cu  ,
,
pentru că dacă\cdot&space;\prod_{i=1}^{n-1}p_i-&space;2m&space;\right&space;)) se divide cu
se divide cu  ,
,
atunci numărul\cdot&space;\prod_{i=1}^{n-1}p_i-&space;2m&space;\right&space;)+k\prod_{i=1}^{n-1}p_i)
nu se divide cu , pentru că k este mai mic decât
, pentru că k este mai mic decât  ,
,
deci nici numărul .
.
La fel de bine, putem scrie numărul într-o altă serie :
într-o altă serie :

+\left&space;(&space;p_n\cdot&space;p_{n-1}-1&space;\right&space;)\prod_{i=1}^{n-1}p_i&space;=)
+\left&space;(&space;p_n\cdot&space;p_{n-1}-2&space;\right&space;)\prod_{i=1}^{n-1}p_i&space;=)
+\left&space;(&space;p_n\cdot&space;p_{n-1}-3&space;\right&space;)\prod_{i=1}^{n-1}p_i&space;=)
...
\cdot&space;\prod_{i=1}^{n-2}p_i-&space;2m&space;\right&space;)+\left&space;(&space;p_n\cdot&space;p_{n-1}-\left&space;(&space;p_n-k&space;\right&space;)&space;\right&space;)\prod_{i=1}^{n-2}p_i)
unde![k\in \left [ 1,\left ( p_n-1 \right ) \right ]](http://latex.codecogs.com/gif.latex?\dpi{110}&space;k\in&space;\left&space;[&space;1,\left&space;(&space;p_n-1&space;\right&space;)&space;\right&space;])
Ca și în situația anterioară, dacă oricare dintre parantezele din stânga seriei de mai sus se divid cu ,
,
atunci numărul nu se divide cu
nu se divide cu  .
.
Explicația este aceeași ca în cazul primei serii prin care am dezvoltat numărul ,
,
constând de altfel în faptul că suma sau diferența a două numere prime între ele nu se divide cu niciun număr prim care divide oricare dintre termenii sumei sau diferenței.
Deci rămâne de analizat situația în care niciuna din parantezele respective, cele din stânga seriilor respective nu se divide cu , fiind posibil în acest fel ca numărul
, fiind posibil în acest fel ca numărul  să poată fi divizibil cu
să poată fi divizibil cu  .
.
Observăm de asemenea, că în ambele serii termenii din paranteze sunt termenii unor progresii aritmetice de rație în prima serie și
în prima serie și  în a doua serie, progresii aritmetice ce conțin ambele
în a doua serie, progresii aritmetice ce conțin ambele  termeni,
termeni,
unde primii termeni ai acestor progresii aritmetice sunt) în prima serie și
în prima serie și ) în a doua serie.
în a doua serie.
Dacă niciun termen\prod_{i=1}^{n-1}p_i-&space;2m&space;\right&space;)) și respectiv
și respectiv \prod_{i=1}^{n-2}p_i-&space;2m&space;\right&space;)) nu se divid cu
nu se divid cu  , atunci vom obține
, atunci vom obține  resturi, în fiecare serie, la împărțirea fiecărui termen
resturi, în fiecare serie, la împărțirea fiecărui termen \prod_{i=1}^{n-1}p_i-&space;2m&space;\right&space;)) și respectiv
și respectiv \prod_{i=1}^{n-2}p_i-&space;2m&space;\right&space;)) prin
prin  .
.
În ambele cazuri, în fiecare serie separat, nu pot exista doi termeni\prod_{i=1}^{n-1}p_i-&space;2m&space;\right&space;)) și
și \prod_{i=1}^{n-1}p_i-&space;2m&space;\right&space;)) astfel încât să aibă amândoi termeni același rest prin împărțirea la
astfel încât să aibă amândoi termeni același rest prin împărțirea la  , pentru că altfel, diferența lor ar trebui să fie divizibilă cu
, pentru că altfel, diferența lor ar trebui să fie divizibilă cu  , în timp ce nu este :
, în timp ce nu este :
\prod_{i=1}^{n-1}p_i-&space;2m&space;\right&space;)-\left&space;(P+\left&space;(&space;p_n-{k}'&space;\right&space;)\prod_{i=1}^{n-1}p_i-&space;2m&space;\right&space;)=)
\prod_{i=1}^{n-1}p_i)
Pentru că atât k', cât și k" sunt mai mici decât înseamnă că diferența lor nu se poate divide cu
înseamnă că diferența lor nu se poate divide cu  și evident, celălalt produs nu-l conține pe
și evident, celălalt produs nu-l conține pe  factor.
factor.
Aceasta înseamnă că în fiecare serie vom obține prin împărțirea parantezelor respective la toate resturile mai mici ca
toate resturile mai mici ca  .
.
Considerăm r fiind restul împărțirii lui) la
la  .
.
În a doua serie există u mai mic ca astfel încât prin împărțirea lui
astfel încât prin împărțirea lui ) la
la  se obține același rest r.
se obține același rest r.
Aceasta înseamnă că diferența
-\left&space;(P+&space;u\cdot&space;\prod_{i=1}^{n-2}p_i-&space;2m&space;\right&space;))
trebuie să fie divizibilă cu pentru că ambele numere au același rest prin împărțirea la
pentru că ambele numere au același rest prin împărțirea la  .
.
Dar diferența de mai sus este\prod_{i=1}^{n-2}p_i) , diferență care nu poate fi divizibilă cu
, diferență care nu poate fi divizibilă cu 
Aceasta înseamnă că unul din cei doi termeni ai diferenței se divide cu , iar de aici rezultă că numărul inițial nu se divide nici cu
, iar de aici rezultă că numărul inițial nu se divide nici cu  .
.
Ce zici Orakle, cum ți se pare ?
Pentru orice număr par 2k există un număr prim P,
Putem verifica afirmația pentru primele câteva numere prime
Dacă vom considera
2=7-5
4=11-7=7-3
...
20=23-3=25-5
Am dat exemplul cu 5+20 =25 pentru că trebuie să fie vorba de un număr impar nedivizibil cu 2 sau 3, nu neapărat prim, așa cum cere și enunțul.
Deci observăm că pentru
La fel de bine, afirmația se verifică ușor prin calcul și pentru numerele prime
Voi încerca să demonstrez prin inducție, considerând că dacă oricare ar fi numărul par 2k și există un număr prim
Considerăm un număr par oarecare 2k.
Acest număr par îl putem scrie ca fiind
Știm că există un număr prim
Dacă numărul
Putem scrie numărul
...
unde
Dacă oricare din termenii scriși în parantezele din stânga ai seriei de mai sus este un număr care se divide cu
pentru că dacă
atunci numărul
nu se divide cu
deci nici numărul
La fel de bine, putem scrie numărul
...
unde
Ca și în situația anterioară, dacă oricare dintre parantezele din stânga seriei de mai sus se divid cu
atunci numărul
Explicația este aceeași ca în cazul primei serii prin care am dezvoltat numărul
constând de altfel în faptul că suma sau diferența a două numere prime între ele nu se divide cu niciun număr prim care divide oricare dintre termenii sumei sau diferenței.
Deci rămâne de analizat situația în care niciuna din parantezele respective, cele din stânga seriilor respective nu se divide cu
Observăm de asemenea, că în ambele serii termenii din paranteze sunt termenii unor progresii aritmetice de rație
unde primii termeni ai acestor progresii aritmetice sunt
Dacă niciun termen
În ambele cazuri, în fiecare serie separat, nu pot exista doi termeni
Pentru că atât k', cât și k" sunt mai mici decât
Aceasta înseamnă că în fiecare serie vom obține prin împărțirea parantezelor respective la
Considerăm r fiind restul împărțirii lui
În a doua serie există u mai mic ca
Aceasta înseamnă că diferența
trebuie să fie divizibilă cu
Dar diferența de mai sus este
Aceasta înseamnă că unul din cei doi termeni ai diferenței se divide cu
Ce zici Orakle, cum ți se pare ?
Ultima editare efectuata de catre curiosul in Vin 18 Iul 2014, 16:11, editata de 1 ori (Motiv : Am modificat concluzia. Cea initiala era greșita)
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
Dacă demonstrația de mai sus este corectă, atunci conjectura lui Goldbach rezultă direct.
La fel și faptul că există o infinitate de numere prime gemene.
Despre aceste implicații voi vorbi mâine, acum nu mai am timp și să lămurim mai întâi corectitudinea acesteia.
La fel și faptul că există o infinitate de numere prime gemene.
Despre aceste implicații voi vorbi mâine, acum nu mai am timp și să lămurim mai întâi corectitudinea acesteia.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
În partea de început am scris :
Însă a fost o greșeală de redactare scrisă în grabă, eram stresat de timp.
Am vrut să spun că numărul par 2k îl putem scrie ca și desigur P+2k sub forma
și desigur P+2k sub forma  .
.
Însă aseară m-am tot gândit și analizat ceea ce am scris aici.
Raționamentul este corect din punct de vedere matematic, însă am un mic dubiu vis-a-vis de o anumită situație raportată la completitudinea demonstrației, ceea ce m-a determinat să încerc să găsesc completarea necesară, dacă este nevoie.
Dar înainte de toate aș vrea să știu dacă are cineva nedumeriri și/sau nevoie de explicații suplimentare.
Poate pe alocuri nu m-am exprimat suficient de clar și detaliat.
Aseară, dacă tot n-am putut să dorm, am găsit raționamentul care demonstrează și conjectura lui Andrica, dacă demonstrația de mai sus este corectă.
Însă s-o validăm pe aceasta scrisă mai sus, mai întâi.
Intuitiv, cred că o mare parte din ipotezele formulate pentru numerele prime se pot demonstra cu ajutorul acesteia.
Deci, are cineva ceva de întrebat referitor la anumite aspecte și nu înțelege exact cum rezultă anumite concluzii din demonstrația de mai sus ?
Pentru că într-adevăr, mie însumi mi se pare că pe alocuri nu este explicat complet cum rezultă anumite deducții și impune un efort suplimentar și din partea cititorului.
curiosul a scris:Considerăm un număr par oarecare 2k.
Acest număr par îl putem scrie ca fiind
Însă a fost o greșeală de redactare scrisă în grabă, eram stresat de timp.
Am vrut să spun că numărul par 2k îl putem scrie ca
Însă aseară m-am tot gândit și analizat ceea ce am scris aici.
Raționamentul este corect din punct de vedere matematic, însă am un mic dubiu vis-a-vis de o anumită situație raportată la completitudinea demonstrației, ceea ce m-a determinat să încerc să găsesc completarea necesară, dacă este nevoie.
Dar înainte de toate aș vrea să știu dacă are cineva nedumeriri și/sau nevoie de explicații suplimentare.
Poate pe alocuri nu m-am exprimat suficient de clar și detaliat.
Aseară, dacă tot n-am putut să dorm, am găsit raționamentul care demonstrează și conjectura lui Andrica, dacă demonstrația de mai sus este corectă.
Însă s-o validăm pe aceasta scrisă mai sus, mai întâi.
Intuitiv, cred că o mare parte din ipotezele formulate pentru numerele prime se pot demonstra cu ajutorul acesteia.
Deci, are cineva ceva de întrebat referitor la anumite aspecte și nu înțelege exact cum rezultă anumite concluzii din demonstrația de mai sus ?
Pentru că într-adevăr, mie însumi mi se pare că pe alocuri nu este explicat complet cum rezultă anumite deducții și impune un efort suplimentar și din partea cititorului.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
Am mai găsit o greșeală de redactare pentru că am postat stresat de timp :
Evident, în al doilea termen al sumelor respective este vorba despre produsul tuturor numerelor prime până la și nu până la
și nu până la 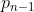 .
.
Deci corect ar fi fost :
La fel de bine, putem scrie numărul într-o altă serie :
într-o altă serie :

+\left&space;(&space;p_n\cdot&space;p_{n-1}-1&space;\right&space;)\prod_{i=1}^{n-2}p_i&space;=)
+\left&space;(&space;p_n\cdot&space;p_{n-1}-2&space;\right&space;)\prod_{i=1}^{n-2}p_i&space;=)
+\left&space;(&space;p_n\cdot&space;p_{n-1}-3&space;\right&space;)\prod_{i=1}^{n-2}p_i&space;=)
...
\cdot&space;\prod_{i=1}^{n-2}p_i-&space;2m&space;\right&space;)+\left&space;(&space;p_n\cdot&space;p_{n-1}-\left&space;(&space;p_n-k&space;\right&space;)&space;\right&space;)\prod_{i=1}^{n-2}p_i)
unde![k\in \left [ 1,\left ( p_n-1 \right ) \right ]](http://latex.codecogs.com/gif.latex?\dpi{110}&space;k\in&space;\left&space;[&space;1,\left&space;(&space;p_n-1&space;\right&space;)&space;\right&space;])
curiosul a scris:La fel de bine, putem scrie numărulîntr-o altă serie :
...
unde
Evident, în al doilea termen al sumelor respective este vorba despre produsul tuturor numerelor prime până la
Deci corect ar fi fost :
La fel de bine, putem scrie numărul
...
unde
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
În rest, totul pare să fie corect redactat matematic.
Oricum, dacă mai există vreo greșeală aceea este de redactare, pentru că în mintea mea raționamentul trebuie să fie corect cap-coadă.
Deci, are cineva nevoie de explicații suplimentare ?
Orakle, mă bazez pe tine, pe părerile tale !
Tu mi-ai cam înțeles tiparul, și noi am mai avut discuții care urmează o linie logică asemănătoare.
Sincer, am nevoie de măcar părerea ta.
O să-ți spun și unde am dubiul de incoerență logică referitor la completitudinea matematică a demonstrației, dar cred că am găsit și raționamentul care o completează, dacă cumva este nevoie de ceva în plus în demonstrație, deși mă îndoiesc, dar totuși, eu am mici, mici dubii undeva.
Și le am pentru că vreau ceva perfect, fără niciun fel de dubii.
Oricum, dacă mai există vreo greșeală aceea este de redactare, pentru că în mintea mea raționamentul trebuie să fie corect cap-coadă.
Deci, are cineva nevoie de explicații suplimentare ?
Orakle, mă bazez pe tine, pe părerile tale !
Tu mi-ai cam înțeles tiparul, și noi am mai avut discuții care urmează o linie logică asemănătoare.
Sincer, am nevoie de măcar părerea ta.
O să-ți spun și unde am dubiul de incoerență logică referitor la completitudinea matematică a demonstrației, dar cred că am găsit și raționamentul care o completează, dacă cumva este nevoie de ceva în plus în demonstrație, deși mă îndoiesc, dar totuși, eu am mici, mici dubii undeva.
Și le am pentru că vreau ceva perfect, fără niciun fel de dubii.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
Curiosule !
Din capul locului nu pricep mare lucru din ce iti propui tu aici.Lasa-mi ceva timp sa vad despre ce este vorba
Din capul locului nu pricep mare lucru din ce iti propui tu aici.Lasa-mi ceva timp sa vad despre ce este vorba
Vizitator- Vizitator
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
Bine ai revenit orakle !
Nu-i corectă demonstrația, dar n-am mai scris nimic pentru că nu mă băga nimeni în seamă.
Dar încearcă să înțelegi ceva pentru că o să-ți scriu ceva ce poate fi dezvoltat în continuare pe baza a ceea ce am scris mai sus.
Nu-i corectă demonstrația, dar n-am mai scris nimic pentru că nu mă băga nimeni în seamă.
Dar încearcă să înțelegi ceva pentru că o să-ți scriu ceva ce poate fi dezvoltat în continuare pe baza a ceea ce am scris mai sus.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
De fapt, Orakle, recitind-o, demonstrația nu este tocmai greșită, dar este o chestie despre care nu sunt sigur că poate conduce la un raționament complet.
Și este un aspect din partea de început, ceva referitor la numărul prim P ales.
Nu satisface o condiție anume și încă nu-mi dau seama dacă este sau nu este un aspect care să invalideze concluzia.
Așa, în mare, ea este bine gândită, dar, când ai timp, mai vorbim despre ea.
Și este un aspect din partea de început, ceva referitor la numărul prim P ales.
Nu satisface o condiție anume și încă nu-mi dau seama dacă este sau nu este un aspect care să invalideze concluzia.
Așa, în mare, ea este bine gândită, dar, când ai timp, mai vorbim despre ea.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
Nu ezita să pui vreo întrebare.
Ca să te scutesc de redactare inutilă, citează doar ceea ce nu înțelegi cum este dedus exact și o să încerc să-ți detaliez cât de complet și ușor de înțeles se poate, sau pot eu.
Ca să te scutesc de redactare inutilă, citează doar ceea ce nu înțelegi cum este dedus exact și o să încerc să-ți detaliez cât de complet și ușor de înțeles se poate, sau pot eu.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41563
Data de inscriere : 22/03/2011
 Re: Are cineva vreo idee ?
Re: Are cineva vreo idee ?
curiosul a scris:Nu ezita să pui vreo întrebare.
Ca să te scutesc de redactare inutilă, citează doar ceea ce nu înțelegi cum este dedus exact și o să încerc să-ți detaliez cât de complet și ușor de înțeles se poate, sau pot eu.
Ok.Saptamana asta sunt cam prins cu alte treburi dar saptamana viitoare promit ca imi rup timp si discutam.
Vizitator- Vizitator
 Subiecte similare
Subiecte similare» Mecanica FOIP si actiunea acestuia asupra corpurilor. (secţiunea 2)
» A incercat cineva dintre noi?
» Au vreo valoare teoriile lui sandokhan?
» A incercat cineva dintre noi?
» Au vreo valoare teoriile lui sandokhan?
Pagina 1 din 1
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 