Ultimele subiecte
» Dovezi ce atestă existența lui DUMNEZEU și că EL este UNICUL CREATOR al UniversuluiScris de virgil Astazi la 18:06
» Unde a ajuns stiinta ?
Scris de virgil Astazi la 18:02
» Ce anume "generează" legile fizice?
Scris de virgil Astazi la 17:45
» Ce fel de popor suntem
Scris de virgil Astazi la 17:40
» Eu sunt Dumnezeu - viitoarea mea carte in limba romana
Scris de Forever_Man Ieri la 09:16
» ChatGPT este din ce în ce mai receptiv
Scris de Meteorr Sam 23 Noi 2024, 21:12
» În ce tip de dovezi aveţi încredere deplină?
Scris de Dacu2 Sam 23 Noi 2024, 15:18
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la CAdi în OZN in Romania
( 1 )
» Mesaj de la CAdi în OZN in Romania
( 1 )
» Mesaj de la CAdi în TEORIA CONSPIRATIEI NU ESTE UN MIT...
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12466) | ||||
| CAdi (12400) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7964) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3970) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Dacu2 | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 15 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 15 Vizitatori :: 1 Motor de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
– Geometria fractala a universului –
+2
CAdi
Razvan
6 participanți
Pagina 3 din 3
Pagina 3 din 3 •  1, 2, 3
1, 2, 3
 – Geometria fractala a universului –
– Geometria fractala a universului –
Rezumarea primului mesaj :
Această teorie, mai bine zis „Ipoteză de lucru”, pleacă de la observaţia existenţei unor similitudini între Universul mare şi cel mic, mai exact a existenţei unui anumit tipar al formelor de manifestare a materiei, de tip fractal.
Există 3 mărimi „fundamentale”, timp, spatiu, masă, în funcţie de care noi suntem obişnuiţi să raportăm tot ceea ce există. Ei bine, voi încerca să verific dacă poate fi găsită o altfel de relaţie între aceste mărimi, o transformare de tip fractal a uneia în alta.
Din start, voi defini câteva dintre noţiunile folosite mai departe:
Numim „dimensiuni” acele caracteristici geometrice pe care le poate avea un obiect; respectiv, dispunerea sa după 3 axe ortogonale, x, y, z. (lungime, lăţime, înălţime).
Numim „scară de mărime” poziţia relativă la care se raportează un observator faţă de unul din celelalte sisteme considerate la un moment dat de referinţă, respectiv al timpului, spaţiului sau al masei.
În fizica de până acum suntem obişnuiţi să alocăm oricărui sistem de referinţă 3 dimensiuni spaţiale şi una temporală. Asta conduce, în anumite situaţii, la apariţia unor nedeterminări, cum sunt singularităţile, sau chiar mai mult, la necesitatea introducerii unor dimensiuni suplimentare. Tot odată mai ştim că nimic nu poate fi divizat la infinit, ci acest lucru este limitat de aşa-numitele „cuante ale lui Planck” (timpul Planck -tp, spaţiul Planck -sp, masa Planck –mp). Sub acest aspect nu putem defini ce se află sub valori mai mici ale acestor constante pentru nici una din mărimile pe care le reprezintă.
Pentru a fi mai intuitiv voi folosi exemplul următor: Un melc se deplasează rectiliniu, urmând să parcurgă o anumită distanţă. Noi dispunem de o unitate de măsură etalon egală cu 1 metru. Ei bine, dacă viteza melcului este de, să zicem, 1 m/oră, noi vom putea să ştim unde se află melcul doar după ce acesta parcurge 1 metru, 2 metri, respectiv 3, 4 şi aşa mai departe. Nu vom putea stabili unde se află melcul după, de exemplu, 1 oră şi 30 de minute. Ştim doar că după 1 oră a parcurs primul metru şi că în decursul celor 30 de minute se află undeva în cel de-al doi-lea metru, dar nu vom putea măsura precis unde se află, deoarece nu dispunem de o unitate de măsură mai mică de 1 metru. Asta înseamnă, în exemplul dat, că ne situăm la o „scară de mărime” la nivelul metrului. Pentru a putea aprecia poziţia melcului mai precis, va trebui să ne raportăm la o altă scară de mărime, respectiv a centimetrului sau milimetrului.
Tot astfel, de la „scara noastră de mărime”, noi percepem spaţiul, timpul şi masa.
Ce s-ar întâmpla însă cu un observator situat la nivelul spaţiului Planck ? Ar percepe ca spaţiu ceea ce noi percepem ca timp ? Şi ca timp (pentru el) ceva ce noi nu avem încă definit, fiind situat sub ordinul de mărime al timpului Planck ? Mai mult, ceea ce pentru noi reprezintă o cuantă de masă (masa Planck) pentru el ar putea reprezenta tot universul ?
Pentru a putea răspunde la aceste întrebări va trebui să vedem dacă putem stabili o relaţie de transformare între aceste mărimi fundamentale (tp, sp, mp).
Adică:
Deci ce avem de făcut este să vedem dacă putem găsi o relaţie între x , y, respectiv 1, astfel încăt aceştia să fie termenii unei progresii. Dacă vom demonstra asta vom putea implicit stabili şi care este raţia acelei progresii, deci vom putea determina orice alt termen al ei, mai mic decât timpul Planck sau mai mare decât masa Planck.
Valorile constantelor lui Planck:

Din aceste valori ne dăm seama că exponenţii x, respectiv y, nu pot fi numere întregi, deci transformările pot fi considerate a fi de tip fractal. Ceea ce, de altfel, observăm şi în natură şi anume că mai nimic nu este definit de numere întregi.
Pentru a exemplifica mai bine voi da exemplu de un fractal: fulgul de zăpadă.
O caracteristică cheie a fractalilor este un parametru matematic numit dimensiunea fractală. Spre deosebire de dimensiunea euclideană, dimensiunea fractală este în general exprimată de un număr fracţionar. Dimensiunea fractală poate fi ilustrată considerând un exemplu specific: curba fulgului de zăpadă definită de Helge von Koch în 1904. Este o figură pur matematică cu o simetrie pe şase axe, ca aceea a fulgului de zăpadă natural. Este autosimilar deoarece este alcătuit din trei părţi identice, iar fiecare din ele se dovedeşte a fi făcută din patru părţi care sunt exact versiuni la scară a întregului. Iar fiecare din cele patru părţi, conţin, la rândul lor, patru părţi ce exprimă miniaturi ale întregului. Pentru curba fulgului de zăpadă, factorul de scară la fiecare nivel este trei. Dimensiunea fractală, D, denotă puterea la care trebuie ridicat 3 pentru a rezulta 4 (3D=4). Dimensiunea curbei fulgului de zăpadă este deci:
D = log 4/log 3
În cazul nostru avem:

Pentru ca ideea mea să fie bine înţeleasă să ne imaginăm în felul următor: mai multe cuante de timp determină apariţia (percepţia din punct de vedere al unui observator) a unei cuante de spaţiu. Mai multe cuante de spaţiu (care include fiecare mai multe cuante de timp) determină apariţia (percepţia) unei cuante de masă. Sau, altfel spus, un număr de cuante de timp capătă „calitatea” de spaţiu şi, la rândul său, un număr de cuante de spaţiu capătă „calitatea” de masă. Am folosit termenul de „calitate” pentru a ilustra percepţia pe care o are observatorul situat la o anumită scară de mărime.
Din nou, pentru a fi intuitiv, voi folosi un exemplu: imaginaţi-vă apa dintr-un ocean: dacă avem un microscop suficient de puternic putem să-i percepem structura moleculară; dacă ne aflăm la nivelul suprafeţei oceanului, observăm valurile, dar nu vom putea discerne structura sa moleculară; dacă suntem situaţi suficient de sus deasupra apei o vom percepe ca pe o suprafaţă plană. Aceaşi apă, se manifestă diferit, în funcţie de scara noastră de percepţie.
În aceaşi ordine de idei, un observator situat la scara de mărime a spaţiului Planck va percepe timpul Planck în mod similar cum percepem noi spaţiul. Deci se va putea deplasa prin ceea ce noi definim ca timp la fel cum o facem noi prin spaţiu, adică în 3 direcţii. Probabil că va percepe simultan atât big-bang-ul cât şi Pământul nostru actual, acestea părându-i-se două entităţi situate la o anumită distanţă în ceea ce el percepe ca spaţiu (pentru noi fiind percepută ca timp).
Câteva din implicaţiile acestei teorii ar fi:
1. Nu s-ar mai defini viteza luminii ca fiind o viteză limită decât pentru scara noastră de mărime, fiecare dintre celelalte scări având propria sa viteză limită similară c, dar de valori diferite raportate la noi.
2. Toate celelalte legi fizice rămân valabile, raportate fiind la scara de mărime respectivă.
3. Nu mai este necesară introducerea de tot felul de dimensiuni suplimentare, a altor noţiuni precum „materie întunecată” şi chiar presupusa existenţă a bozonului Higgs nu mai este necesară.
4. Însăşi big-bang-ul nu mai trebuie privit ca o creaţie a universului ci ca pe un punct limită privit doar din postura scării noastre de mărime. Altfel spus, un observator situat la altă scară de mărime ar experimenta big-bang-ul său, diferit de al nostru prin scara de mărime la care acesta l-ar percepe, dar totuşi similar.
De fapt, big-bang-ul reprezintă o „împingere” către limita percepţiei a datelor noastre despre universul în care ne aflăm. Poate că o reprezentare grafică a universului perceput s-ar apropia mai mult de forma asta:

Ei bine, până să trec la analiza mai detaliată a ecuaţiei de mai sus, respectiv

şi până să găsesc raţia progresiei dintre x şi y, aş fi curios să aflu şi alte păreri cu privire la aspectele expuse până acum.
Şi ca o ultimă paranteză, teoria de ultimă oră, cum că universul a avut la început una, apoi două, apoi trei dimensiuni, vine să confirme cele afirmate de mine până acum, şi anume transformarea de tip fractal a unui număr de cuante fundamentale în altă cuantă fundamentală, dar asta doar din punct de vedere al percepţiei asupra scării de mărime respective.
Există 3 mărimi „fundamentale”, timp, spatiu, masă, în funcţie de care noi suntem obişnuiţi să raportăm tot ceea ce există. Ei bine, voi încerca să verific dacă poate fi găsită o altfel de relaţie între aceste mărimi, o transformare de tip fractal a uneia în alta.
Din start, voi defini câteva dintre noţiunile folosite mai departe:
Numim „dimensiuni” acele caracteristici geometrice pe care le poate avea un obiect; respectiv, dispunerea sa după 3 axe ortogonale, x, y, z. (lungime, lăţime, înălţime).
Numim „scară de mărime” poziţia relativă la care se raportează un observator faţă de unul din celelalte sisteme considerate la un moment dat de referinţă, respectiv al timpului, spaţiului sau al masei.
În fizica de până acum suntem obişnuiţi să alocăm oricărui sistem de referinţă 3 dimensiuni spaţiale şi una temporală. Asta conduce, în anumite situaţii, la apariţia unor nedeterminări, cum sunt singularităţile, sau chiar mai mult, la necesitatea introducerii unor dimensiuni suplimentare. Tot odată mai ştim că nimic nu poate fi divizat la infinit, ci acest lucru este limitat de aşa-numitele „cuante ale lui Planck” (timpul Planck -tp, spaţiul Planck -sp, masa Planck –mp). Sub acest aspect nu putem defini ce se află sub valori mai mici ale acestor constante pentru nici una din mărimile pe care le reprezintă.
Pentru a fi mai intuitiv voi folosi exemplul următor: Un melc se deplasează rectiliniu, urmând să parcurgă o anumită distanţă. Noi dispunem de o unitate de măsură etalon egală cu 1 metru. Ei bine, dacă viteza melcului este de, să zicem, 1 m/oră, noi vom putea să ştim unde se află melcul doar după ce acesta parcurge 1 metru, 2 metri, respectiv 3, 4 şi aşa mai departe. Nu vom putea stabili unde se află melcul după, de exemplu, 1 oră şi 30 de minute. Ştim doar că după 1 oră a parcurs primul metru şi că în decursul celor 30 de minute se află undeva în cel de-al doi-lea metru, dar nu vom putea măsura precis unde se află, deoarece nu dispunem de o unitate de măsură mai mică de 1 metru. Asta înseamnă, în exemplul dat, că ne situăm la o „scară de mărime” la nivelul metrului. Pentru a putea aprecia poziţia melcului mai precis, va trebui să ne raportăm la o altă scară de mărime, respectiv a centimetrului sau milimetrului.
Tot astfel, de la „scara noastră de mărime”, noi percepem spaţiul, timpul şi masa.
Ce s-ar întâmpla însă cu un observator situat la nivelul spaţiului Planck ? Ar percepe ca spaţiu ceea ce noi percepem ca timp ? Şi ca timp (pentru el) ceva ce noi nu avem încă definit, fiind situat sub ordinul de mărime al timpului Planck ? Mai mult, ceea ce pentru noi reprezintă o cuantă de masă (masa Planck) pentru el ar putea reprezenta tot universul ?
Pentru a putea răspunde la aceste întrebări va trebui să vedem dacă putem stabili o relaţie de transformare între aceste mărimi fundamentale (tp, sp, mp).
Adică:

Deci ce avem de făcut este să vedem dacă putem găsi o relaţie între x , y, respectiv 1, astfel încăt aceştia să fie termenii unei progresii. Dacă vom demonstra asta vom putea implicit stabili şi care este raţia acelei progresii, deci vom putea determina orice alt termen al ei, mai mic decât timpul Planck sau mai mare decât masa Planck.
Valorile constantelor lui Planck:

Din aceste valori ne dăm seama că exponenţii x, respectiv y, nu pot fi numere întregi, deci transformările pot fi considerate a fi de tip fractal. Ceea ce, de altfel, observăm şi în natură şi anume că mai nimic nu este definit de numere întregi.
Pentru a exemplifica mai bine voi da exemplu de un fractal: fulgul de zăpadă.
O caracteristică cheie a fractalilor este un parametru matematic numit dimensiunea fractală. Spre deosebire de dimensiunea euclideană, dimensiunea fractală este în general exprimată de un număr fracţionar. Dimensiunea fractală poate fi ilustrată considerând un exemplu specific: curba fulgului de zăpadă definită de Helge von Koch în 1904. Este o figură pur matematică cu o simetrie pe şase axe, ca aceea a fulgului de zăpadă natural. Este autosimilar deoarece este alcătuit din trei părţi identice, iar fiecare din ele se dovedeşte a fi făcută din patru părţi care sunt exact versiuni la scară a întregului. Iar fiecare din cele patru părţi, conţin, la rândul lor, patru părţi ce exprimă miniaturi ale întregului. Pentru curba fulgului de zăpadă, factorul de scară la fiecare nivel este trei. Dimensiunea fractală, D, denotă puterea la care trebuie ridicat 3 pentru a rezulta 4 (3D=4). Dimensiunea curbei fulgului de zăpadă este deci:
D = log 4/log 3
În cazul nostru avem:

Pentru ca ideea mea să fie bine înţeleasă să ne imaginăm în felul următor: mai multe cuante de timp determină apariţia (percepţia din punct de vedere al unui observator) a unei cuante de spaţiu. Mai multe cuante de spaţiu (care include fiecare mai multe cuante de timp) determină apariţia (percepţia) unei cuante de masă. Sau, altfel spus, un număr de cuante de timp capătă „calitatea” de spaţiu şi, la rândul său, un număr de cuante de spaţiu capătă „calitatea” de masă. Am folosit termenul de „calitate” pentru a ilustra percepţia pe care o are observatorul situat la o anumită scară de mărime.
Din nou, pentru a fi intuitiv, voi folosi un exemplu: imaginaţi-vă apa dintr-un ocean: dacă avem un microscop suficient de puternic putem să-i percepem structura moleculară; dacă ne aflăm la nivelul suprafeţei oceanului, observăm valurile, dar nu vom putea discerne structura sa moleculară; dacă suntem situaţi suficient de sus deasupra apei o vom percepe ca pe o suprafaţă plană. Aceaşi apă, se manifestă diferit, în funcţie de scara noastră de percepţie.
În aceaşi ordine de idei, un observator situat la scara de mărime a spaţiului Planck va percepe timpul Planck în mod similar cum percepem noi spaţiul. Deci se va putea deplasa prin ceea ce noi definim ca timp la fel cum o facem noi prin spaţiu, adică în 3 direcţii. Probabil că va percepe simultan atât big-bang-ul cât şi Pământul nostru actual, acestea părându-i-se două entităţi situate la o anumită distanţă în ceea ce el percepe ca spaţiu (pentru noi fiind percepută ca timp).
Câteva din implicaţiile acestei teorii ar fi:
1. Nu s-ar mai defini viteza luminii ca fiind o viteză limită decât pentru scara noastră de mărime, fiecare dintre celelalte scări având propria sa viteză limită similară c, dar de valori diferite raportate la noi.
2. Toate celelalte legi fizice rămân valabile, raportate fiind la scara de mărime respectivă.
3. Nu mai este necesară introducerea de tot felul de dimensiuni suplimentare, a altor noţiuni precum „materie întunecată” şi chiar presupusa existenţă a bozonului Higgs nu mai este necesară.
4. Însăşi big-bang-ul nu mai trebuie privit ca o creaţie a universului ci ca pe un punct limită privit doar din postura scării noastre de mărime. Altfel spus, un observator situat la altă scară de mărime ar experimenta big-bang-ul său, diferit de al nostru prin scara de mărime la care acesta l-ar percepe, dar totuşi similar.
De fapt, big-bang-ul reprezintă o „împingere” către limita percepţiei a datelor noastre despre universul în care ne aflăm. Poate că o reprezentare grafică a universului perceput s-ar apropia mai mult de forma asta:

Ei bine, până să trec la analiza mai detaliată a ecuaţiei de mai sus, respectiv

şi până să găsesc raţia progresiei dintre x şi y, aş fi curios să aflu şi alte păreri cu privire la aspectele expuse până acum.
Şi ca o ultimă paranteză, teoria de ultimă oră, cum că universul a avut la început una, apoi două, apoi trei dimensiuni, vine să confirme cele afirmate de mine până acum, şi anume transformarea de tip fractal a unui număr de cuante fundamentale în altă cuantă fundamentală, dar asta doar din punct de vedere al percepţiei asupra scării de mărime respective.
_________________
Eşti inteligent atunci când crezi doar jumătate din ceea ce afli; eşti înţelept atunci când ştii care jumătate!

Razvan- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 6183




Puncte : 33845
Data de inscriere : 18/03/2011
 Re: – Geometria fractala a universului –
Re: – Geometria fractala a universului –
Ar fi frumos sa fie asa ,dar nu cred ca s-a inspirat cineva de pe forumul nostru.
Pur si simplu este o coincidenta de studiu!
Nu a colaborat nimeni si de altfel cei care au deschis subiectele respective si-au dat numele si au avut pareri
oarecum diferite desi modul lor de analiza are lacune ,pentru ca in studiul fractalitatii nu se porneste de la
curbe ci de la linia franta. Cum a fost exemplul cu fulgul...
Linia perfect curba reprezinta idealul, dar nu exista in Univers !
Daca vroiau sa se inspire puteau lua ca model curba Koch :
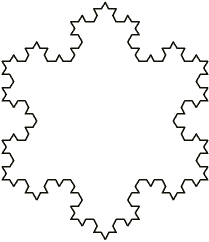
Pur si simplu este o coincidenta de studiu!
Nu a colaborat nimeni si de altfel cei care au deschis subiectele respective si-au dat numele si au avut pareri
oarecum diferite desi modul lor de analiza are lacune ,pentru ca in studiul fractalitatii nu se porneste de la
curbe ci de la linia franta. Cum a fost exemplul cu fulgul...
Linia perfect curba reprezinta idealul, dar nu exista in Univers !
Daca vroiau sa se inspire puteau lua ca model curba Koch :
CAdi- Foarte activ

- Numarul mesajelor : 12400
Data de inscriere : 16/02/2011
 Re: – Geometria fractala a universului –
Re: – Geometria fractala a universului –
5 dimensiuni? 4? 100? 15 mici 25 mari? e inutil să ne dăm cu părerea astfel, ghicind cîte ar trebui să fie, batem pasul pe loc!
cît timp nu știm de ce neapărat 3 dimensiuni și, cel puțin eu, nu suntem convinși de necesitatea axiomei « avem 3 dimensiuni spațiale » , de ce trei și nu două sau una!?, nu n-avem cum demonstra că sunt 5 sau 6, ceea ce eu oricum mă îndoiesc!
orice extra-dimensiune, înțeleasă ca o libertate de mișcare suplimentară, maximul la care a ajuns matematica contemporană cît am putut-o pricepe eu, poate fi redusă la una mai mică!
exemplu banal, pretenția că spinul face o mișcare de rotație de 720⁰ și de aici afirmația că e o rotație în mai multe dimensiuni poate fi demonstrat că e o concluzie falsă și inutilă, de care nu e nevoie
să ne imaginăm o sferă goală, M, cu o altă sferă în interiorul ei, N, cu același punct ca centru, care se vor roti una în jurul celeilalte cu viteze diferite ... prima sferă, M, se rotește cu viteza 2A în jurul axei verticale, Y, cealaltă, N, cu viteza A, jumătate din cealaltă viteză ...
cît încă sferele nu se mișcă una față de cealaltă marcăm un punct oarecare pe suprafața sferei M, T, altul decît polii nord și sud prin care trece axa de rotație, și punctul corespunzător, K, pe sfera N care e determinat de linia care unește T cu centrul celor două sfere și care înțeapă suprafața sferei N
sferele stau nemișcate => starea A
rotim cele două sfere, una cu viteza 2V cealaltă doar V
cînd sfera M a făcut o rotație de 360⁰ sfera interioară, N, face o rotație de doar 180⁰ => starea B
cînd sfera M ajunge la 720⁰, două rotații complete, sfera N face și ea una completă, de 360⁰ => starea C
se poate demonstra ușor, logic și rațional ca să priceapă oricine, că A≢C în timp și A≡C în spațiu și din asta deducem că A=C, aceeași stare, în timp ce B≠A deci B≠C și în timp și în spațiu ceea ce ne determină să spunem că avem o stare diferită ...
și pentru o astfel de rotație, de 720⁰, în spațiul 3D al ansamblului format din cele două sfere care îl putem considera un mecanism, un obiect distinct, n-avem nevoie de nici un fel de dimensiune suplimentară!
deștepții fizicii moderne insistă că electronul se rotește în mai multe dimensiuni pentru ca ei pretind în mod nejustificat că electronul ar fi o particulă elementară, fără părți independente care să se miște autonom, în plus și fără dimensiuni, un simplu punct în spațiu!
și deaia pentru că spinul se rotește 720⁰ n-are cum se roti altfel decît în mai multe dimensiuni!
ete scîrț! și dacă nu e particulă elementară?! dacă sfera M în cazul electronului, care devine sfera N, e întregul univers!?
e explicație mai simplă? mie așa îmi pare! mai logică și mai rațională? parcă!
briciul lui occam intră în acțiune și taie cu poftă:
concluzie: n-avem nevoie de nici o extradimensiune, mai mică sau mai mare, ca să putem descrie în mod logic și rațional mișcarea de spin a electronului cu 720⁰ în jurul lui însuși! e inutilă și nenaturală!
există explicații mult mai simple și mai naturale!
cît despre dimensiunile fractale, asta e cu totul altceva! pare interesantă direcția, ar putea să ne ajute să definim mai clar ideea de spațiu și dimensiuni, și astfel să înțelegem de ce spațiul 3 3D și cu 2D sau 1D sau 4D și de ce aparent timpul e doar 1D și în plus și ca orientare doar dinspre trecut spre viitor ...
nasul meu miroase că e o direcție corectă de cercetat pentru că o dimensiune fractală ia în calcul și relația dintre parte și întreg, ceea ce nu se întîmplă în spațiul 3D clasic în care raportul parte|întreg e inrelevant dpdv al definirii și înțelegerii clasice a ce e un spațiu 3D ... e 3D că așa a vrut mușchiul lui decartes și că matematica și fizica de la el pînă în zilele noastre n-a reușit decît să spună că are dreptate, aparent în spațiu ne putem mișca 3D ...
cît timp nu știm de ce neapărat 3 dimensiuni și, cel puțin eu, nu suntem convinși de necesitatea axiomei « avem 3 dimensiuni spațiale » , de ce trei și nu două sau una!?, nu n-avem cum demonstra că sunt 5 sau 6, ceea ce eu oricum mă îndoiesc!
orice extra-dimensiune, înțeleasă ca o libertate de mișcare suplimentară, maximul la care a ajuns matematica contemporană cît am putut-o pricepe eu, poate fi redusă la una mai mică!
exemplu banal, pretenția că spinul face o mișcare de rotație de 720⁰ și de aici afirmația că e o rotație în mai multe dimensiuni poate fi demonstrat că e o concluzie falsă și inutilă, de care nu e nevoie
să ne imaginăm o sferă goală, M, cu o altă sferă în interiorul ei, N, cu același punct ca centru, care se vor roti una în jurul celeilalte cu viteze diferite ... prima sferă, M, se rotește cu viteza 2A în jurul axei verticale, Y, cealaltă, N, cu viteza A, jumătate din cealaltă viteză ...
cît încă sferele nu se mișcă una față de cealaltă marcăm un punct oarecare pe suprafața sferei M, T, altul decît polii nord și sud prin care trece axa de rotație, și punctul corespunzător, K, pe sfera N care e determinat de linia care unește T cu centrul celor două sfere și care înțeapă suprafața sferei N
sferele stau nemișcate => starea A
rotim cele două sfere, una cu viteza 2V cealaltă doar V
cînd sfera M a făcut o rotație de 360⁰ sfera interioară, N, face o rotație de doar 180⁰ => starea B
cînd sfera M ajunge la 720⁰, două rotații complete, sfera N face și ea una completă, de 360⁰ => starea C
se poate demonstra ușor, logic și rațional ca să priceapă oricine, că A≢C în timp și A≡C în spațiu și din asta deducem că A=C, aceeași stare, în timp ce B≠A deci B≠C și în timp și în spațiu ceea ce ne determină să spunem că avem o stare diferită ...
și pentru o astfel de rotație, de 720⁰, în spațiul 3D al ansamblului format din cele două sfere care îl putem considera un mecanism, un obiect distinct, n-avem nevoie de nici un fel de dimensiune suplimentară!
deștepții fizicii moderne insistă că electronul se rotește în mai multe dimensiuni pentru ca ei pretind în mod nejustificat că electronul ar fi o particulă elementară, fără părți independente care să se miște autonom, în plus și fără dimensiuni, un simplu punct în spațiu!
și deaia pentru că spinul se rotește 720⁰ n-are cum se roti altfel decît în mai multe dimensiuni!
ete scîrț! și dacă nu e particulă elementară?! dacă sfera M în cazul electronului, care devine sfera N, e întregul univers!?
e explicație mai simplă? mie așa îmi pare! mai logică și mai rațională? parcă!
briciul lui occam intră în acțiune și taie cu poftă:
concluzie: n-avem nevoie de nici o extradimensiune, mai mică sau mai mare, ca să putem descrie în mod logic și rațional mișcarea de spin a electronului cu 720⁰ în jurul lui însuși! e inutilă și nenaturală!
există explicații mult mai simple și mai naturale!
cît despre dimensiunile fractale, asta e cu totul altceva! pare interesantă direcția, ar putea să ne ajute să definim mai clar ideea de spațiu și dimensiuni, și astfel să înțelegem de ce spațiul 3 3D și cu 2D sau 1D sau 4D și de ce aparent timpul e doar 1D și în plus și ca orientare doar dinspre trecut spre viitor ...
nasul meu miroase că e o direcție corectă de cercetat pentru că o dimensiune fractală ia în calcul și relația dintre parte și întreg, ceea ce nu se întîmplă în spațiul 3D clasic în care raportul parte|întreg e inrelevant dpdv al definirii și înțelegerii clasice a ce e un spațiu 3D ... e 3D că așa a vrut mușchiul lui decartes și că matematica și fizica de la el pînă în zilele noastre n-a reușit decît să spună că are dreptate, aparent în spațiu ne putem mișca 3D ...
 Re: – Geometria fractala a universului –
Re: – Geometria fractala a universului –
Razvan a scris:Tot căutând pe internet, după anumite cuvinte cheie, am dat peste ceva: două site-uri, pe care văd că a fost preluată
săi tragem de urechi pe năzdrăvani, jmecheri micii drăcușori, cu drepturile de autori nu te joci!
Pagina 3 din 3 •  1, 2, 3
1, 2, 3
 Subiecte similare
Subiecte similare» Geometria numerelor prime
» Inventie romaneasca – Turbina gravitationala
» O altă perspectivă asupra transformărilor relativiste – posibile implicaţii
» Inventie romaneasca – Turbina gravitationala
» O altă perspectivă asupra transformărilor relativiste – posibile implicaţii
Pagina 3 din 3
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 