Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Meteorr Astazi la 17:13
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 1 )
» Mesaj de la Abel Cavaşi în Daci nemuritori
( 1 )
» Mesaj de la CAdi în Fenomene Electromagnetice
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12458) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Dacu2 | ||||
| Forever_Man | ||||
| Abel Cavaşi | ||||
| Meteorr |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| Dacu2 | ||||
| virgil | ||||
| CAdi | ||||
| eugen | ||||
| ilasus | ||||
| Abel Cavaşi | ||||
| Meteorr |
Spune şi altora
Cine este conectat?
În total sunt 39 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 39 Vizitatori Nici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Reprezentarea grafica a numerelor complexe
+2
negativ
meteor
6 participanți
Pagina 1 din 3
Pagina 1 din 3 • 1, 2, 3 
 Reprezentarea grafica a numerelor complexe
Reprezentarea grafica a numerelor complexe
Nu prea pricep, si chiar nu sunt de acord, ca reprexentarea cutare https://www.youtube.com/watch?v=_7pjdy9BvH0 , spre exemplu, ar fi corecta.
Fie am dori sa reprezentam in planul complex numarul i.
Si ce avem ?!
Ca i se afla pe axa imaginara cu lungimea =1, axa reala ia valori 0.
In loc a scrie Axa Imaginara foarte ok merge sa scriem si dreapta reala y.
Nu pricep.
Fie am dori sa reprezentam in planul complex numarul i.
Si ce avem ?!
Ca i se afla pe axa imaginara cu lungimea =1, axa reala ia valori 0.
In loc a scrie Axa Imaginara foarte ok merge sa scriem si dreapta reala y.
Nu pricep.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Eu nu pricep ce nu pricepi ! 
Exprima-te mai clar poate mai impusc un zece
Exprima-te mai clar poate mai impusc un zece
Vizitator- Vizitator
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Mezei Geza a scris:
Exprima-te mai clar poate mai impusc un zece
Se stie ca numerele imaginare sunt in afara numerelor reale.
ok fie avem axa numerelor reale.
ok se stie ce numerele cu partea imaginara nenula vor fi in afara axei numerelor reale.
insa, nu stim cert cum sa reprezentam un anumit numar.
Lumea cica, cam asa ar arata: https://www.google.md/search?q=complex+plane&tbm=isch&tbo=u&source=univ&sa=X&ei=5lCRUZ2IHMHUswar3YGgDA&ved=0CDUQsAQ&biw=1366&bih=587#imgrc=4SeRiJSc12QyVM%3A%3ByEfxCNFv5Q4MLM%3Bhttp%253A%252F%252Fwww.clarku.edu%252F~djoyce%252Fcomplex%252Fplane.gif%3Bhttp%253A%252F%252Fwww.clarku.edu%252F~djoyce%252Fcomplex%252Fplane.html%3B570%3B402 .
Intrebare: Daca pe axa acea Imaginara, vom pune numai numere reale, si din titlul "Axa cu numere imaginare" vom pune " y ", ce e mare noutate aici ?!
Numarul i cin il reprezentam e ok asa ?!
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Daca bine am inteles ce te doare:
Practic nu este nici o noutate doar ca atunci esti in R^2 si nu in C
In acest caz esti in R^2 si multimea este formata din elemente de forma:
S^2=v ori v =a^2+b^2
In multimea numerelor complexe ai elemente de forma:
z=1a+ib
Norma in C este z z*=(a+ib)(a-ib)=a^2+b^2
si nu mai definesti nimic in plus
Norma lui i este 1 o putem reprezenta cu usurinta pe y in locul vectorasului j
Orice numar complex este o combinatie de reale +imaginare si respecta intrutotul algebra unui spatiu vectorial
Sper ca te-am nimerit cu raspunsul
Practic nu este nici o noutate doar ca atunci esti in R^2 si nu in C
In acest caz esti in R^2 si multimea este formata din elemente de forma:
v=ivector ori a +jvector orib
Esti obligat sa definesti produsul scalar sau norma euclidiana S^2=v ori v =a^2+b^2
In multimea numerelor complexe ai elemente de forma:
z=1a+ib
Norma in C este z z*=(a+ib)(a-ib)=a^2+b^2
si nu mai definesti nimic in plus
Norma lui i este 1 o putem reprezenta cu usurinta pe y in locul vectorasului j
Orice numar complex este o combinatie de reale +imaginare si respecta intrutotul algebra unui spatiu vectorial
Sper ca te-am nimerit cu raspunsul
Ultima editare efectuata de catre Mezei Geza in Mar 14 Mai 2013, 00:43, editata de 1 ori (Motiv : -)
Vizitator- Vizitator
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Mezei, daca ma lamuresti cu urmatoarea intrebare, atunci jos palaria.
Intii au fost definite numerele naturale, fiecare le stim, si, cel mai important avem o gramada uriasa de intrebari care imediat se explica in mod practic.
Apoi negative, rationale, irationale, transcendente.
Ca sa ne putem imagina cum ar arata un numar irational sau transcendent, putem construi un patrat cu latura o valoare fiind nepatrat perfect, si poftim diagonala patratului este un numar irational.
Daca vrem sa "vedem" un numar transcendent, spre exemplu putem lua urmatorul caz: Luam pe rigla o lungime oarecare naturala (spre exemplu), construim un cerc cu aceasta lungime, lungimea cercului are o valoare irationala.
Ce exemplu simplu, clar, poti sa imi aduci, astfel incit in el sa fie pus in aplicatie numerele complexe cu partea imaginara nenula ?!
Ada una, cinci, zece exeple practice (ca in cazul de mai sus), de care stii si is mai simple, de care tis mai comode.
Intii au fost definite numerele naturale, fiecare le stim, si, cel mai important avem o gramada uriasa de intrebari care imediat se explica in mod practic.
Apoi negative, rationale, irationale, transcendente.
Ca sa ne putem imagina cum ar arata un numar irational sau transcendent, putem construi un patrat cu latura o valoare fiind nepatrat perfect, si poftim diagonala patratului este un numar irational.
Daca vrem sa "vedem" un numar transcendent, spre exemplu putem lua urmatorul caz: Luam pe rigla o lungime oarecare naturala (spre exemplu), construim un cerc cu aceasta lungime, lungimea cercului are o valoare irationala.
Ce exemplu simplu, clar, poti sa imi aduci, astfel incit in el sa fie pus in aplicatie numerele complexe cu partea imaginara nenula ?!
Ada una, cinci, zece exeple practice (ca in cazul de mai sus), de care stii si is mai simple, de care tis mai comode.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Sa ne intelegem:
Vrei un exemplu practic in care "problema" se rezolva cu ajutorul numerelor complexe?
Cam asta am inteles eu
Vrei un exemplu practic in care "problema" se rezolva cu ajutorul numerelor complexe?
Cam asta am inteles eu
Vizitator- Vizitator
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Da-mi un exemplu din viata (care se poate pune in practica, aplicatie, care se poate verifica, experimenta), in care in joc sunt numerele imaginare.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
In linii mari orice problema plana se poate rezolva si cu ajutorul numerelor complexe.
Teoria numerelor complexe e una vasta,dar rezumand aplicatile la un nivel mediu ramanem doar cu aplicatia geometrica ca reprezentare de un punct(asa numitul plan complex) sau ca spatiu afin de vectori mult mai apropiat de notiunile din fizica caracterizate vectorial.
Orice reprezentare grafica a unei oscilatii,camp magnetic sau gravitational si altele pot fi vazute ca valori complexe intrucat majoritatea evenimentelor fizice de acest gen au loc intr-un plan.
Cele mai simple exemple sunt:
1-miscarea circurara si miscarea oscilatorie armonica:
http://ro.math.wikia.com/wiki/Mi%C8%99care_oscilatorie_armonic%C4%83
2- analiza complexa a circuitelor electrice:
http://www.regentsprep.org/Regents/math/algtrig/ATO6/electricalresouce.htm
In principiu numerele complexe ne conduc la rezultate mult mai elegante
Pacat ca nu ti-am gasit niste linkuri mai explicite (stiu sigur ca sunt pagini si cu explicatii mai bune dar ghinion vad ca acuma nu dau de ele)
Teoria numerelor complexe e una vasta,dar rezumand aplicatile la un nivel mediu ramanem doar cu aplicatia geometrica ca reprezentare de un punct(asa numitul plan complex) sau ca spatiu afin de vectori mult mai apropiat de notiunile din fizica caracterizate vectorial.
Orice reprezentare grafica a unei oscilatii,camp magnetic sau gravitational si altele pot fi vazute ca valori complexe intrucat majoritatea evenimentelor fizice de acest gen au loc intr-un plan.
Cele mai simple exemple sunt:
1-miscarea circurara si miscarea oscilatorie armonica:
http://ro.math.wikia.com/wiki/Mi%C8%99care_oscilatorie_armonic%C4%83
2- analiza complexa a circuitelor electrice:
http://www.regentsprep.org/Regents/math/algtrig/ATO6/electricalresouce.htm
In principiu numerele complexe ne conduc la rezultate mult mai elegante
Pacat ca nu ti-am gasit niste linkuri mai explicite (stiu sigur ca sunt pagini si cu explicatii mai bune dar ghinion vad ca acuma nu dau de ele)
Ultima editare efectuata de catre Mezei Geza in Mar 14 Mai 2013, 14:54, editata de 1 ori (Motiv : corectie)
Vizitator- Vizitator
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
- Axa de anumita multime, sau plan sau spatiu de reprezentare a anumitor multimi de numere, care sa fie curb (aceasta venind desigur din proprietatile acestor numere care le respecta), cum crezi are sens, sau e o gogoasa ?! Daca pot fi da niste exemple.
- Se stie, spre exemplu, ca sin x = cu raportul a doua numere reale.
Daca spui ca ai priceput cit de cit numerele complexe, atunci spune cit va fi (desigur poate ca lucrul ar putea sa-ti usureze cea mai inportanta formula din stiinta- formula lui Euler):
sin x; arcsin x (aceasta la caz general);
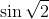 ;
; 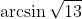 (niste cazuri particulare).
(niste cazuri particulare).
Daca se poate da raspuns la intrebarile astea din urma, atunci cred ca nu mai este ce de rezolvat in stiinta.
- Se stie, spre exemplu, ca sin x = cu raportul a doua numere reale.
Daca spui ca ai priceput cit de cit numerele complexe, atunci spune cit va fi (desigur poate ca lucrul ar putea sa-ti usureze cea mai inportanta formula din stiinta- formula lui Euler):
sin x; arcsin x (aceasta la caz general);
Daca se poate da raspuns la intrebarile astea din urma, atunci cred ca nu mai este ce de rezolvat in stiinta.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
1-Se poate si pe multimi "curbe" dar nu are nici un sens.Multimea "curba" o poti descrie usor cu o multime "dreapta" plus o functie care face legatura.
O multime cum zici tu ar fi o complicatie inutila.
De fapt daca nu gresesc prin schimbarii de variabile cam asta faci definesti axe"curbe"
2-la aceasta intrebare ti-ai dat singur raspunsul
(Formula lui Euler)
Nu stiu daca este ce amai importanta formula dar sigur este cea mai frumoasa !!
O singura observatie:
"Se stie, spre exemplu, ca sin x = cu raportul a doua numere reale"
Sau raportul a doua numere complexe cu partea reala zero (ia/ia")
Nu de alta dar sa nu te incurci in :
sinx=(e^ix-e^-ix)/2i
O multime cum zici tu ar fi o complicatie inutila.
De fapt daca nu gresesc prin schimbarii de variabile cam asta faci definesti axe"curbe"
2-la aceasta intrebare ti-ai dat singur raspunsul
(Formula lui Euler)
Nu stiu daca este ce amai importanta formula dar sigur este cea mai frumoasa !!
O singura observatie:
"Se stie, spre exemplu, ca sin x = cu raportul a doua numere reale"
Sau raportul a doua numere complexe cu partea reala zero (ia/ia")
Nu de alta dar sa nu te incurci in :
sinx=(e^ix-e^-ix)/2i
Vizitator- Vizitator
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Nu inteleg, de ce cu partea reala zero ?!Mezei Geza a scris:
O singura observatie:
"Se stie, spre exemplu, ca sin x = cu raportul a doua numere reale"
Sau raportul a doua numere complexe cu partea reala zero (ia/ia")
Nu de alta dar sa nu te incurci in :
sinx=(e^ix-e^-ix)/2i
Ce cind ai un triunghi dreptunghic, laturile lui sunt numere reale cu partea reala zero?!
Sinusul este raportul catetei catre ipotenuza, sau raportul a doua numere complexe cu partea imaginara nula, la care nuitorul permament e mai mare sau egal ca numaratorul.
De ce zici ca sa nu ma incurc cu formula aia?!
In fine, daca stii cum sa calculezi cu o functie trigonometrica, le stii pe restul.
Adica daca nu iti place sinus, si poti lucra cu cosinus, atunci ajungi si la sinus prin transformari.
In fine, care este raspunsul?!
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
1-cu -intre euri este imaginar
cu + este real
Rezulta din formula lui Euler
2
Vrei sin (radical din 2)
grade sexazecimale ?
Treci valoarea unghiului in valori adimensionale (in radiani )
(radical de 2) grade corespunde la
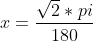
si aplici formula de mai sus
Pentru arcsin si arccos asa retin ca ai o formula similara simpluta (dedusa tot din formula lui Euler -ceva cu un logaritm natural)
Vad ca acuma nu dau de ea daca te interesaza foarte tare pot maine sa o dau de ea sau sa o deduc ca nu este mare branza
Arcsin radical din 13 ?
Arcsin are argumentul intre -1 si 1 nu vad de unde ai inventat valoarea asta
Celalalt arcsin este in regula
cu + este real
Rezulta din formula lui Euler
2
Vrei sin (radical din 2)
grade sexazecimale ?
Treci valoarea unghiului in valori adimensionale (in radiani )
(radical de 2) grade corespunde la
si aplici formula de mai sus
Pentru arcsin si arccos asa retin ca ai o formula similara simpluta (dedusa tot din formula lui Euler -ceva cu un logaritm natural)
Vad ca acuma nu dau de ea daca te interesaza foarte tare pot maine sa o dau de ea sau sa o deduc ca nu este mare branza
Arcsin radical din 13 ?
Arcsin are argumentul intre -1 si 1 nu vad de unde ai inventat valoarea asta
Celalalt arcsin este in regula
Vizitator- Vizitator
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Si inca m-ai luat la 11m cand am zis ca "scriem pe forum si nu analizam inainte ce scriem"
Sper ca nu ai si gradele sub radical ?
Vizitator- Vizitator
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Odata si odata, valori concrete la raspuns poti sa aduci, sau nu ?
Vrei sa te obosesti sa scrii solutia sau nu ?
Grade hexazecimale, centizecimale, radiani etc. acestea is fleacuri (de trecut din una in alta nu e problema, da se poate spune ca e mai bine de lucrat cu radiani), pur si simplu sunt anumite notatii comode in anumite conditii.
Raspunsuri similare ca: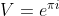 nu ma intereseaza, vreau sa vad asa:
nu ma intereseaza, vreau sa vad asa: 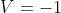
Vrei sa te obosesti sa scrii solutia sau nu ?
Grade hexazecimale, centizecimale, radiani etc. acestea is fleacuri (de trecut din una in alta nu e problema, da se poate spune ca e mai bine de lucrat cu radiani), pur si simplu sunt anumite notatii comode in anumite conditii.
Raspunsuri similare ca:
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Valorile functiilor trigonometrice, in zia de azi, din cite vad, se cunoasc DOAR pe anumite puncte particulare, NU si in cazul orecarui punct luat la caz general.
Se stie de formula lui Euler, ea este extrem importanta (insa e prea compacta ca sa fie inteleasa deplin)
Insa din cauza ca nu poate inca nici un om de pe planeta aceasta sa inteleaga pina la capat (profund) numerele imaginare [dupa parerea mea], se scrie sau nu, in forma bruta ce valoare are functia trigonometrica in un anumit punct.
Exemple/ probleme:
1.) ;
;
2.) ;
;
3.)
etc.
Spre exemplu la punctul 3. putem deduce raspunsul, exact el fiind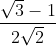 , aceasta e bine, este un raspuns normal, se poate de lucrat, nu e reprezentat ca fiind o aproximatie.
, aceasta e bine, este un raspuns normal, se poate de lucrat, nu e reprezentat ca fiind o aproximatie.
Da se poate intimpla ca solutia sa fie un numar transcendent, ce nu poate fi scris asa compact, insa sa se specifice, ca doar nu o fi in restul punctelor doar numere transcendente.
Se stie de formula lui Euler, ea este extrem importanta (insa e prea compacta ca sa fie inteleasa deplin)
Insa din cauza ca nu poate inca nici un om de pe planeta aceasta sa inteleaga pina la capat (profund) numerele imaginare [dupa parerea mea], se scrie sau nu, in forma bruta ce valoare are functia trigonometrica in un anumit punct.
Exemple/ probleme:
1.
2.
3.
etc.
Spre exemplu la punctul 3. putem deduce raspunsul, exact el fiind
Da se poate intimpla ca solutia sa fie un numar transcendent, ce nu poate fi scris asa compact, insa sa se specifice, ca doar nu o fi in restul punctelor doar numere transcendente.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Este inpropriu spus ca nu se cunosc.Mai exact formele analitice ale unor valori sunt complicate sau inca neexplicitate.
1-Pentru arcsin vezi:
http://www.math.ethz.ch/education/bachelor/lectures/fs2012/other/ka_itet/TrigHypFunktionen.pdf
O sa ma documentez si eu ca par interesante.
2-Ce m-a surprins insa din discututia noastra (asa din vorba in vorba) si m-a facut sa ma aplec mai mult asupra numerelor complexe este scrierea parametrica a spiralei logaritmice.
Chiar daca pare ceva banal forma parametrica a spiralei:
=Ae^{bt}cos(t))
=Ae^{bt}sin(t))
Aplicand formula lui Euler va fi:
=A\frac{\left (e^{bt+it}+e^{bt-it} \right )}{2i})
=A\frac{\left (e^{bt+it}-e^{bt-it} \right )}{2i})
Eventual notam=iz)
Respectiv conjugatul lui :=-iz^{^{\star }})
rezulta:
=A\frac{\left (e^{iz}+e^{-iz^{\star }} \right )}{2})
=A\frac{\left (e^{iz}-e^{-iz^{\star }} \right )}{2i})
Solutii frumoase pline de caracter care posibil candva sa ne fie de ajutor
care posibil candva sa ne fie de ajutor 
1-Pentru arcsin vezi:
http://www.math.ethz.ch/education/bachelor/lectures/fs2012/other/ka_itet/TrigHypFunktionen.pdf
O sa ma documentez si eu ca par interesante.
2-Ce m-a surprins insa din discututia noastra (asa din vorba in vorba) si m-a facut sa ma aplec mai mult asupra numerelor complexe este scrierea parametrica a spiralei logaritmice.
Chiar daca pare ceva banal forma parametrica a spiralei:
Aplicand formula lui Euler va fi:
Eventual notam
Respectiv conjugatul lui :
rezulta:
Solutii frumoase pline de caracter
Vizitator- Vizitator
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Aceasta deja e cutotul alta vorba.Mezei Geza a scris:Este inpropriu spus ca nu se cunosc.Mai exact formele analitice ale unor valori sunt complicate sau inca neexplicitate.
Neintelegerea acelor formule, eu cred, ca vine de la aceea ca nu este inteles perfect pina la capat ce inseamna unitatea imaginara.
Se lucreaza mai mult orbeste.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
meteor a scris:
Neintelegerea acelor formule, eu cred, ca vine de la aceea ca nu este inteles perfect pina la capat ce inseamna unitatea imaginara.
Se lucreaza mai mult orbeste.
Corect
Si asta asa va si ramane.Sintem incapabili sa percepem prin analogie intrutotul aceste numere.
Facem o analogie cu un plan real bidimensional dar asta nu ne rezolva decat "varful eisbergului"
Vizitator- Vizitator
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
meteor a scris:Insa din cauza ca nu poate inca nici un om de pe planeta aceasta sa inteleaga pina la capat (profund) numerele imaginare [dupa parerea mea], se scrie sau nu, in forma bruta ce valoare are functia trigonometrica in un anumit punct.
Planul complex reprezintã toate relaţiile care privesc un punct material, referitoare la starea trecutã si viitoare, care îi determinã evolutia în spaţiul real, adicã spaţiul realitãtii fizice, înafara transformãrilor geometrice impuse de referentialul ortogonal ales, deci planul Argand constituie spaţiul unde se manifestã si se exprimã concomitent cu planul real, diverse proprietãţi ale punctului material
.meteor a scris:Da se poate întîmpla ca solutia sa fie un numar transcendent, ce nu poate fi scris asa compact, insa sa se specifice, ca doar nu o fi in restul punctelor doar numere transcendente.
Pe axa realã poti stabili numere transcendente oriunde doresti , cu exceptia întregilor si a valorii zero, adãugînd un numãr infinit de zecimale aleatoare la unitate. Între valoarea de 3,2 si 3,3 poti obtine o infinitate de puncte, la fel ca si în cazul valorilor 2 si 3. Radical din 3 e transcendent ?
Asta e cam cît pot sã explic eu, dar mie cel putin mi se pare clar.
Asta e cam cît pot sã explic eu, dar mie cel putin mi se pare clar.
_________________
N∃GATIV
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Eu ridic alta problema :
De ce la partea reala a numerelor este nevoie si de o parte imaginara ?
Partea reala nu este suficienta ? Ce aduce in plus un numar complex?
De ce la partea reala a numerelor este nevoie si de o parte imaginara ?
Partea reala nu este suficienta ? Ce aduce in plus un numar complex?
CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12397




Puncte : 59038
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Nu inteleg ce ai lamuritnegativ a scris:meteor a scris:Da se poate întîmpla ca solutia sa fie un numar transcendent, ce nu poate fi scris asa compact, insa sa se specifice, ca doar nu o fi in restul punctelor doar numere transcendente.Pe axa realã poti stabili numere transcendente oriunde doresti , cu exceptia întregilor si a valorii zero, adãugînd un numãr infinit de zecimale aleatoare la unitate. Între valoarea de 3,2 si 3,3 poti obtine o infinitate de puncte, la fel ca si în cazul valorilor 2 si 3. Radical din 3 e transcendent ?
Asta e cam cît pot sã explic eu, dar mie cel putin mi se pare clar.
Valorile functiilor trigonomice (sin, cos, spre exemplu), sunt in intervalul [-1,1].
Care era problema ridicata de mine ?!
Era aceea caci din formula lui Euler sa aducem solutia la un mod normal, inteligibil (adica fara unitatea ceea imaginara).
Insa, se stie ca nu toate numerele se pot aduce la asaforma, spre exemplu: e, PI, 1/e, 1/PI, etc.
Intradevar asa numere is infinite.
Dar, daca am avea ca in anumit punct functia are un numar transcendent sa se specifice ca asa este, daca nu, sa se aduca la forma normala.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Cadi, eu nu inteleg problema ta.CAdi a scris:Eu ridic alta problema :
De ce la partea reala a numerelor este nevoie si de o parte imaginara ?
Partea reala nu este suficienta ? Ce aduce in plus un numar complex?
Poate trebue ceva sa mai recapitulezi din acest curs de matematematica.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
meteor a scris:Cadi, eu nu inteleg problema ta.CAdi a scris:Eu ridic alta problema :
De ce la partea reala a numerelor este nevoie si de o parte imaginara ?
Partea reala nu este suficienta ? Ce aduce in plus un numar complex?
Poate trebue ceva sa mai recapitulezi din acest curs de matematematica.
Poate...poate ar trebui sa raspunda altcineva.(Eu am pus problema asa cum o pui si tu la inceputul topicului
dar din alt punct de vedere.)
Se stie ca matematica are corespondenta in realitate si tot ceea ce a fost conceput de om (in afara de coliba
care a fost ridicata de omul din Neanderthal si de uneltele si armele lui primitive) a fost construit si fabricat pe baza unor principii fizice si calcule matematice precise ....Mezei Geza a dat niste exemple...
CAdi- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 12397




Puncte : 59038
Data de inscriere : 16/02/2011
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
meteor a scris:Care era problema ridicata de mine ?!
Era aceea caci din formula lui Euler sa aducem solutia la un mod normal, inteligibil (adica fara unitatea ceea imaginara).
Dar, daca am avea ca in anumit punct functia are un numar transcendent sa se specifice ca asa este, daca nu, sa se aduca la forma normala.
Matematica pe care o înveti în primii ani de scoalã este o simplificare pentru a întelege cum functioneazã aparatul matematic. Dacã nu întelegi cã în realitate toate numerele sunt complexe, inclusiv multimea numerelor naturale, iar numerele asa-zis reale sunt niste numere complexe cu coeficienti zero la partea complexã, sã încerc altceva : daca spargi o piatrã ce obtii ? Douã pietre sau douã jumãtãti de piatrã ? Rãspunsul corect ar fi cã în mod natural obtii douã pietre si în mod real, ai douã jumãtãti . Dacã extrapolezi asta si la numerele complexe, e perfect !
Concluzia e cã în mod fizic, 1=0*1+0*i . Matematica desparte cele douã multimi, C si R, doar pentru simplificare.
Concluzia e cã în mod fizic, 1=0*1+0*i . Matematica desparte cele douã multimi, C si R, doar pentru simplificare.
_________________
N∃GATIV
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
Eu stiam ca orice numar inmultit cu zero, da tot zero, asa ca suma de mai sus are ca rezultat tot zero si nu unu, iar zero nu inseamna un numar, ci lipsa oricarui numar.1=0*1+0*i
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Reprezentarea grafica a numerelor complexe
Re: Reprezentarea grafica a numerelor complexe
virgil a scris:Eu stiam ca orice numar inmultit cu zero, da tot zero, asa ca suma de mai sus are ca rezultat tot zero si nu unu, iar zero nu inseamna un numar, ci lipsa oricarui numar.1=0*1+0*i
Scuze, 1+0*i, iar 0 poate însemna rezultatul unei expresii în zona complexã. Si 0 nu stiu dacã este un numãr sau o valoare a unui numãr. Din punct de vedere matematic, 0 este un loc în plan, ca si în spatiul fizic. Mã voi gîndi. Important e cã orice punct din spatiul real (nu matematic), are o valoare imaginarã, suprapusã peste cea realã, observabilã. Cu sistemul matematic... e mai greu, dar el se vede cã respectã exact relatiile fizice, fiind de fapt construit pe baza acestora, de-a lungul timpului, pe bazã de observatii.
_________________
N∃GATIV
Pagina 1 din 3 • 1, 2, 3 
Pagina 1 din 3
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 