Forum pentru cercetare
Doriți să reacționați la acest mesaj? Creați un cont în câteva clickuri sau conectați-vă pentru a continua.
Forum pentru cercetare

O platformă românească pentru schimbul de idei necesar descoperirilor importante. Construim aici un loc potrivit pentru toţi vorbitorii de limba română pasionaţi de cercetare. Lăsaţi orice prejudecată, cei ce intraţi aici!

„Prostul nu e prost destul dacă nu e și fudul.” (proverb românesc)
„Adevărul nu învinge niciodată; pier doar adversarii lui.” (Max Planck)
„Lumea nu e a celor care pot, ci a celor care vor.” (Johann Wolfgang von Goethe)
„Toate faptele și gândurile mari au un început ridicol.” (Albert Camus)
„Cinismul de orice fel este o mască pentru neputinţa de adaptare.” (John Fowles)
„Prefer de departe cele mai aprigi critici ale unui om inteligent decât aprobarea nechibzuită a maselor.” (Johannes Kepler)
„Șiretenia și perfidia sunt resursele oamenilor care nu au destulă minte pentru a fi cinstiți.” (Benjamin Franklin)
„A nu fi sigur este, cred, unul dintre lucrurile esenţiale ale raţionalităţii.” (Bertrand Russell)
„Ştiinţa este încrederea în ignoranţa experţilor.” (Richard Feynman)
„Nu te atinge de cercurile mele!” (Arhimede)
„Fie vom găsi o cale, fie vom face una.” (Hannibal)
„Voi lupta până la ultima mea picătură de sânge ca să ai dreptul să nu fii de acord cu mine!” (Ion Rațiu)
„Nu recunosc alt semn al superiorităţii decât bunătatea.” (Ludwig van Beethoven)
„Minţile ilustre discută idei; minţile mediocre discută evenimente; minţile mici discută oamenii.” (Socrate)
„Violenţa este ultimul refugiu al incompetenţei.” (Isaac Asimov)
„Trebuie să supui îndoielii tot ce poate fi pus la îndoială, doar astfel se poate descoperi ce nu poate fi pus la îndoială.” (Tadeusz Kotarbiński)
„Un vapor este în siguranţă în port, dar vapoarele nu sunt făcute ca să zacă în porturi.” (William Shedd)
„Uneori oamenii nu vor să audă adevărul, deoarece nu vor să le fie distruse iluziile.” (Friedrich Nietzsche)
„Prea des noi ne bucurăm de confortul unei opinii fără disconfortul cugetării.” (John F. Kennedy)
„Nu e obligatoriu să fii de acord cu mine. Dar ar fi mai rapid aşa.” (Albert Einstein)
„Dacă nu poţi explica un lucru unui copil de şase ani, atunci nici tu nu îl înţelegi.” (Albert Einstein)
Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romana
Scris de Forever_Man Ieri la 22:56

» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31

» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57

» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07

» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00

» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26

» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50

» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30

» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44

» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05

» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06

» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14

» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59

» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56

» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06

» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04

» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11

» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43

» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01

» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51

» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34

» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59

» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01

» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06

» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03

» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57

» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50

» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37

» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49

» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37

Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină?
( 2 )


» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )


» Mesaj de la CAdi în Ce anume "generează" legile fizice?
( 1 )


» Mesaj de la CAdi în OZN in Romania
( 1 )


» Mesaj de la eugen în Global warming is happening?
( 1 )


Subiectele cele mai vizionate
Ce este FOIP?
Legi de conservare (1)
Bancuri......
Legi de conservare (2)
Lucrul mecanic - definitie si exemple
Mecanica FOIP si actiunea acestuia asupra corpurilor.(secţiunea 4)
Lucrul mecanic - definitie si exemple (Secţiunea 2)
TEORIA CONSPIRATIEI NU ESTE UN MIT...
Laborator-sa construim impreuna
Eterul, eterul

Subiectele cele mai active
Mecanica FOIP si actiunea acestuia asupra corpurilor.(secţiunea 3)
Bancuri......
Legi de conservare (2)
Despre credinţă şi religie
propuneri ...
Eterul, eterul
Lucrul mecanic - definitie si exemple
Ce a fost inainte de Big-Bang? Alte aspecte in Univers
Urme ale extraterestrilor pe Pamant; Descoperiri inexplicabile (in cache)
Ce fel de popor suntem

Top postatori
virgil (12458)
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
CAdi (12397)
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
virgil_48 (11380)
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
Abel Cavaşi (7963)
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
gafiteanu (7617)
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
curiosul (6790)
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
Razvan (6183)
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
Pacalici (5571)
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
scanteitudorel (4989)
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
eugen (3969)
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 

Cei care creeaza cel mai des subiecte noi
Abel Cavaşi
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
Pacalici
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
CAdi
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
curiosul
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
Dacu
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
Razvan
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
virgil
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
meteor
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
gafiteanu
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
scanteitudorel
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 

Cei mai activi postatori ai lunii
virgil
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
No_name
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
CAdi
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
ilasus
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
eugen
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
Dacu2
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
Forever_Man
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
Abel Cavaşi
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 

Cei mai activi postatori ai saptamanii
Forever_Man
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
Dacu2
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
virgil
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
CAdi
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
ilasus
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
eugen
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 
Abel Cavaşi
Modalități de demonstrare a conjecturii lui Goldbach Vote_lcapModalități de demonstrare a conjecturii lui Goldbach Voting_barModalități de demonstrare a conjecturii lui Goldbach Vote_rcap 

Cuvinte-cheie

Inventatori  7  suntem  daci  bancuri  sondaj  Propuneri  mecanic  este  sanatate  68  PROTEST  2  popor  Fenomene  Tesla  EMdrive  stiinta  foip  teoria  Eterul  Newton  Maxwell  timp  timpul  lucrul  

Flux RSS


Yahoo! 
MSN 
AOL 
Netvibes 
Bloglines 


Parteneri
forum gratuit
free counters
Spune şi altora
Cine este conectat?
În total sunt 40 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 40 Vizitatori :: 1 Motor de căutare

Nici unul

Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare

Modalități de demonstrare a conjecturii lui Goldbach

Forum pentru cercetare :: Cercetări în Matematică :: Probleme nerezolvate în Matematică

In jos

Modalități de demonstrare a conjecturii lui Goldbach Empty Modalități de demonstrare a conjecturii lui Goldbach

Mesaj Scris de curiosul Mier 18 Feb 2015, 17:19

O modalitate interesantă și ceva mai utilă pentru demonstrarea conjecturii lui Goldbach este cea prezentată mai jos.

Conjectura lui Goldbach presupune că orice număr par este suma a două numere prime.
Se poate verifica adevărul acestei presupuneri pentu numere pare destul de mari.
Fie


Dacă presupunem că numărul par 2n, suficient de mare, este considerat că nu se poate scrie ca sumă de două numere prime, atunci putem stabili că produsele    și   sunt numere prime între ele.
Pentru că dacă 2n nu se scrie ca sumă două numere prime, atunci primul produs se va divide doar cu numere prime mai mici decât n, în timp ce al doilea produs se divide doar cu numerele prime cuprinse între n și 2n.
Factorii primului produs, fiind diferențele dintre 2n și orice număr prim impar mai mic ca n, iar 2n nu este suma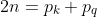 ,   nu poate conține în factorizare niciun număr prim mai mare ca n, pentru că altfel, dacă se divide cu un număr prim mai mare ca n, atunci este mai mare ca 2n, ceea ce este imposibil.

Deci dacă numărul par 2n nu poate fi scris ca sumă de două numere prime, atunci cele două produse sunt prime între ele.

De aici putem deduce că diferența



este o diferență care nu se divide cu niciun prim mai mic ca 2n.
Dacă există două numere prime între ele, să spunem u și v, astfel încât ambii termeni ai diferenței de mai jos sunt numere prime între ele



înseamnă că numărul par 2n se scrie ca sumă de două numere prime.

Pentru că diferența, fiind un număr mai mic decât , înseamnă că trebuie să se dividă obligatoriu cu un număr prim mai mic decât .
Iar aceasta este adevărat doar dacă unul din factorii produsului se divide cu un număr prim mai mic ca , iar acel număr prim este conținut și în celălalt produs , iar de aici rezultă că 2n se scrie ca sumă de două numere prime.

Deci, generalizat, ar trebui demonstrat că oricare ar fi a și b prime între ele, există c și d prime între ele, astfel încât ac-bd să fie cuprins într-un anumit interval, în cazul nostru, într-un interval cuprins între 2n și cu ac și bd prime între ele.

curiosul
Banat temporar pentru comportamentul nepotrivit

Mulţumit de forum :
Modalități de demonstrare a conjecturii lui Goldbach Left_bar_bleue10 / 1010 / 10Modalități de demonstrare a conjecturii lui Goldbach Right_bar_bleue
Numarul mesajelor : 6790
Puncte : 41551
Data de inscriere : 22/03/2011

Sus In jos

Sus

- Subiecte similare

Forum pentru cercetare :: Cercetări în Matematică :: Probleme nerezolvate în Matematică

 
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum