Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Forever_Man Ieri la 22:56
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la eugen în Global warming is happening?
( 1 )
» Mesaj de la CAdi în TEORIA CONSPIRATIEI NU ESTE UN MIT...
( 1 )
» Mesaj de la CAdi în Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12458) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Spune şi altora
Cine este conectat?
În total sunt 19 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 19 Vizitatori Nici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Conjectura Beal
2 participanți
Pagina 2 din 3
Pagina 2 din 3 •  1, 2, 3
1, 2, 3 
 Conjectura Beal
Conjectura Beal
Rezumarea primului mesaj :
Enunțul acestei conjecturi afirmă faptul că ecuația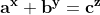 are soluții pentru x, y, z mai mari ca 2, doar dacă a, b, c au un divizor comun.
are soluții pentru x, y, z mai mari ca 2, doar dacă a, b, c au un divizor comun.
Să încercăm să dezvoltăm în acest subiect modalități de demonstrare a acestei conjecturi.
În primul rând, ceea ce este evident și rezultă direct este faptul că dacă această ecuație are soluții care nu sunt prime între ele, deci au un divizor comun, atunci prin simplificare cu acel divizor, ecuația ajunge să aibă și soluții prime între ele, pentru acele valori x, y, z.
Deci ar trebui analizate soluțiile primitive ale ecuației.
Problema care se ridică în această situație este alta.
Este suficient să demonstrăm că ecuația nu are soluții primitive, pentru ca să rezulte că dacă ea are soluții, atunci acestea nu sunt prime între ele ?
Pentru că aceasta cere de fapt enunțul conjecturii.
Trebuie arătat că dacă ecuația are soluții, atunci soluțiile a, b, c au un divizor comun.
Din punctul meu de vedere, conjectura se rezumă doar la a demonstra că ecuația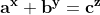 nu are soluții a, b, c prime între ele.
nu are soluții a, b, c prime între ele.
Dacă nu are soluții primitive, atunci fie ecuația nu are soluții, fie ecuația are soluții a, b, c, dar acestea nu sunt prime între ele, ci au un divizor comun.
Dar apare imposibilitatea prin faptul că dacă ecuația are soluții a, b, c care au un divizor comun, atunci are și soluții prime între ele.
Cu alte cuvinte, demonstrația este făcută doar prin menționarea aspectului de mai sus.
Dacă ecuația are soluții, are obligatoriu soluții prime între ele.
Așa cum rezultă din raționamentul de mai jos :
Considerăm x, y, z diferite, fără să aibă importanță care dintre ele este mai mare ca oricare alta.
Considerăm numărul p divizorul comun al acestora.
Ecuația devine :
^x+(p{b}')^y=(p{c}')^z})
Simplificăm prin divizorul comun p la cea mai mică putere (presupunem că această putere este x prin condiția pusă (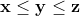 ) iar ecuația devine :
) iar ecuația devine :
^x+p^{y-x}({b}')^y=p^{z-x}({c}')^z})
Ecuație care deasemenea poate fi scrisă
^x=p^{z-x}({c}')^z-p^{y-x}({b}')^y})
Dacă z este mai mare ca y, de aici rezultă că în termenul din dreapta egalității mai poate fi scos factorul comun p , pentru că z-x>y-x :
![\dpi{150} \mathbf{({a}')^x=p^{y-x}[p^{z-y}({c}')^z-({b}')^y]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{({a}')^x=p^{y-x}[p^{z-y}({c}')^z-({b}')^y]})
De aici rezultă că egalitatea de mai sus este adevărată doar dacă termenul din stânga se divide cu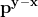 .
.
Dar de asemenea rezultă că a' se divide cu p și nu numai, din egalitatea la care sa ajuns, rezultă că p trebuie să fie cel puțin la puterea x în factorizarea lui^x}) .
.
Din condiția pusă,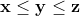 , rezultă că
, rezultă că
^x=p^{y-x}p^s({a}'')^x})
unde y-x+s=x.
Înlocuind în ecuația la care s-a ajuns valoarea de mai sus, egalitatea devine :
![\dpi{150} \mathbf{({a}')^x=p^{y-x}[p^{z-y}({c}')^z-({b}')^y]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{({a}')^x=p^{y-x}[p^{z-y}({c}')^z-({b}')^y]})
![\dpi{150} \mathbf{p^{y-x}p^s({a}'')^x=p^{y-x}[p^{z-y}({c}')^z-({b}')^y]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{p^{y-x}p^s({a}'')^x=p^{y-x}[p^{z-y}({c}')^z-({b}')^y]})
^x=p^{z-y}({c}')^z-({b}')^y})
Egalitate pe care o putem aduce la forma
^y=p^{z-y}({c}')^z-p^s({a}'')^x})
Din egalitatea de mai sus putem scoate în termenul din dreapta factorul comun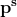 iar egalitatea devine
iar egalitatea devine
![\dpi{150} \mathbf{({b}')^y=p^s[p^{z-y-s}({c}')^z-({a}'')^x]}](http://latex.codecogs.com/gif.latex?\dpi{150} \mathbf{({b}')^y=p^s[p^{z-y-s}({c}')^z-({a}'')^x]})
de unde rezultă că b' trebuie să se dividă din nou cu p.
Se pare că am ajuns în situația anterioară și vom ajunge în aceeași situație ori de câte ori vom continua raționamentul pe același principiu.
Dar continuând în același mod raționamentul vom ajunge să arătăm că una din valorile a, b este exact divizorul comun al soluțiilor a, b, c.
Carevasăzică, forma ecuației inițiale, plecând de la presupunerea că soluțiile a, b, c au divizorul comun p, va deveni
^y=(a\cdot c)^z})
Simplificând ecuația prin a la puterea x , aceasta devine
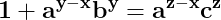
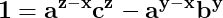
Dacă z este mai mare ca y, atunci în partea dreaptă a egalității îl putem scoate factor comun pe a, ceea ce ar însemna că 1 se divide cu a. Evident fals, dacă a este mai mare ca 1, egalitatea de mai sus neavând, de altfel, niciun fel de soluții netriviale.
Pentru că soluțiile triviale ale ecuației de mai sus sunt de altfel și soluțiile triviale ale ecuației inițiale, acestea ies din calcul.
În consecință, am arătat că plecând de la ipoteza că ecuația ar avea soluții a, b, c, având toate un divizor comun p, se ajunge la a arăta că ecuația nu are soluții.
Ecuația ar putea avea soluții dacă soluțiile a, b, c sunt soluții primitive și prime între ele.
Deci vis-a-vis de acestă conjectura am arătat exact inversul.
Ea poate avea soluții doar dacă a, b, c sunt prime între ele, nicidecum că ele trebuie să aibă proprietatea că au un divizor comun.
Ciudată întorsătură de situație.
Raționamentul prezentat mai sus este dezvoltat așa la repezeală și s-ar putea să nu fie corect, dar sper să dea idei și altora care știu cum să fructifice concluziile mele.
Aștept oricum, feedback-urile voastre, să vedem ce putem corecta.
Enunțul acestei conjecturi afirmă faptul că ecuația
Să încercăm să dezvoltăm în acest subiect modalități de demonstrare a acestei conjecturi.
În primul rând, ceea ce este evident și rezultă direct este faptul că dacă această ecuație are soluții care nu sunt prime între ele, deci au un divizor comun, atunci prin simplificare cu acel divizor, ecuația ajunge să aibă și soluții prime între ele, pentru acele valori x, y, z.
Deci ar trebui analizate soluțiile primitive ale ecuației.
Problema care se ridică în această situație este alta.
Este suficient să demonstrăm că ecuația nu are soluții primitive, pentru ca să rezulte că dacă ea are soluții, atunci acestea nu sunt prime între ele ?
Pentru că aceasta cere de fapt enunțul conjecturii.
Trebuie arătat că dacă ecuația are soluții, atunci soluțiile a, b, c au un divizor comun.
Din punctul meu de vedere, conjectura se rezumă doar la a demonstra că ecuația
Dacă nu are soluții primitive, atunci fie ecuația nu are soluții, fie ecuația are soluții a, b, c, dar acestea nu sunt prime între ele, ci au un divizor comun.
Dar apare imposibilitatea prin faptul că dacă ecuația are soluții a, b, c care au un divizor comun, atunci are și soluții prime între ele.
Cu alte cuvinte, demonstrația este făcută doar prin menționarea aspectului de mai sus.
Dacă ecuația are soluții, are obligatoriu soluții prime între ele.
Așa cum rezultă din raționamentul de mai jos :
Considerăm x, y, z diferite, fără să aibă importanță care dintre ele este mai mare ca oricare alta.
Considerăm numărul p divizorul comun al acestora.
Ecuația devine :
Simplificăm prin divizorul comun p la cea mai mică putere (presupunem că această putere este x prin condiția pusă (
Ecuație care deasemenea poate fi scrisă
Dacă z este mai mare ca y, de aici rezultă că în termenul din dreapta egalității mai poate fi scos factorul comun p , pentru că z-x>y-x :
De aici rezultă că egalitatea de mai sus este adevărată doar dacă termenul din stânga se divide cu
Dar de asemenea rezultă că a' se divide cu p și nu numai, din egalitatea la care sa ajuns, rezultă că p trebuie să fie cel puțin la puterea x în factorizarea lui
Din condiția pusă,
unde y-x+s=x.
Înlocuind în ecuația la care s-a ajuns valoarea de mai sus, egalitatea devine :
Egalitate pe care o putem aduce la forma
Din egalitatea de mai sus putem scoate în termenul din dreapta factorul comun
de unde rezultă că b' trebuie să se dividă din nou cu p.
Se pare că am ajuns în situația anterioară și vom ajunge în aceeași situație ori de câte ori vom continua raționamentul pe același principiu.
Dar continuând în același mod raționamentul vom ajunge să arătăm că una din valorile a, b este exact divizorul comun al soluțiilor a, b, c.
Carevasăzică, forma ecuației inițiale, plecând de la presupunerea că soluțiile a, b, c au divizorul comun p, va deveni
Simplificând ecuația prin a la puterea x , aceasta devine
Dacă z este mai mare ca y, atunci în partea dreaptă a egalității îl putem scoate factor comun pe a, ceea ce ar însemna că 1 se divide cu a. Evident fals, dacă a este mai mare ca 1, egalitatea de mai sus neavând, de altfel, niciun fel de soluții netriviale.
Pentru că soluțiile triviale ale ecuației de mai sus sunt de altfel și soluțiile triviale ale ecuației inițiale, acestea ies din calcul.
În consecință, am arătat că plecând de la ipoteza că ecuația ar avea soluții a, b, c, având toate un divizor comun p, se ajunge la a arăta că ecuația nu are soluții.
Ecuația ar putea avea soluții dacă soluțiile a, b, c sunt soluții primitive și prime între ele.
Deci vis-a-vis de acestă conjectura am arătat exact inversul.
Ea poate avea soluții doar dacă a, b, c sunt prime între ele, nicidecum că ele trebuie să aibă proprietatea că au un divizor comun.
Ciudată întorsătură de situație.
Raționamentul prezentat mai sus este dezvoltat așa la repezeală și s-ar putea să nu fie corect, dar sper să dea idei și altora care știu cum să fructifice concluziile mele.
Aștept oricum, feedback-urile voastre, să vedem ce putem corecta.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
Geza,
când ai timp, aruncă o privire aici.
Sau mai detaliat aici.
Hai să discutăm "oleacă" despre aceste analize.
Părerile oricui vrea să se implice sunt binevenite.
când ai timp, aruncă o privire aici.
Sau mai detaliat aici.
Hai să discutăm "oleacă" despre aceste analize.
Părerile oricui vrea să se implice sunt binevenite.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Numarul mesajelor : 6790
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
Din punctul meu de vedere, demonstrația nu urmează o linie de implicare directă.
Tu ce părere ai ?
Tu ce părere ai ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Numarul mesajelor : 6790
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
curiosul a scris:Geza,
când ai timp, aruncă o privire aici.
Sau mai detaliat aici.
Hai să discutăm "oleacă" despre aceste analize.
Părerile oricui vrea să se implice sunt binevenite.
Ideea prin care analizează autorul egalitatea, mi se pare totuși interesantă.
Se observă că termenul din dreapta egalității poate fi scris în funcție de celelalte, într-o formă asemănătoare expresiei lui delta din gradul 2.
Cum ar fi oare, dacă plecând de la această idee, am aduce egalitatea conjecturii lui Beal la o ecuație de gradul 2 ?
Tu ce zici ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
curiosul a scris:curiosul a scris:Geza,
când ai timp, aruncă o privire aici.
Sau mai detaliat aici.
Hai să discutăm "oleacă" despre aceste analize.
Părerile oricui vrea să se implice sunt binevenite.
Ideea prin care analizează autorul egalitatea, mi se pare totuși interesantă.
Se observă că termenul din dreapta egalității poate fi scris în funcție de celelalte, într-o formă asemănătoare expresiei lui delta din gradul 2.
Cum ar fi oare, dacă plecând de la această idee, am aduce egalitatea conjecturii lui Beal la o ecuație de gradul 2 ?
Tu ce zici ?
Pe mine m-a depasit de la relatia notata cu (5) dar stilul pompos deja da de banuit
Am dat o cautare dupa numele lui nu am gasit rezultate foarte optimiste.Parerea mea este ca tipul este un Woddy american cu un pic mai multa scoala ca si al nostru.
Vezi mesajul 1485 din Forum de aici rezulta ca tipul este total in aer si din cate am inteles eu din discutie tind sa le dau drepate.
Vizitator- Vizitator
 Re: Conjectura Beal
Re: Conjectura Beal
Pare că da !
Oricum, merită aprofundată, cel puțin de către mine, să înțeleg mai bine anumite lucruri și cine știe, poate-mi mai dă idei.
Aia cu ecuația de gradul 2 nu are sorți de izbândă.
Le-am amestecat un pic pe hârtie, dar tot la a demonstra ecuația inițială se ajunge.
Dacă mai găsești astfel de demonstrații faimoase, pune-le aici să le analizăm.
Oricum, merită aprofundată, cel puțin de către mine, să înțeleg mai bine anumite lucruri și cine știe, poate-mi mai dă idei.
Aia cu ecuația de gradul 2 nu are sorți de izbândă.
Le-am amestecat un pic pe hârtie, dar tot la a demonstra ecuația inițială se ajunge.
Dacă mai găsești astfel de demonstrații faimoase, pune-le aici să le analizăm.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
În primul rând Geza, în demonstrația propriu zisă, este analizată doar valoarea c^z.
Este menționat un pic la început egalitatea ecuației, după care ceea ce este analizat în continuare nu mai are nicio treabă cu valorile a^x și b^y.
Este analizată strict, și izolat, doar valoarea c^z, valoare pentru care nu este menționată și implicată direct faptul că ea este suma a^x+b^y, ele putând fi orice fel de valori, pentru că nu mai sunt luate în calcul.
Situație în care nu implică în niciun fel adevărul conjecturii.
Nu există o relație directă care să implice egalitatea ecuației.
Peste tot pe unde a folosit c, ar fi trebuit să folosească suma respectivă, sub radical sau nu, să ajungă la concluzia că ele au un divizor comun. Dar iară nu e o implicație directă, pentru că poate alege oricare valori, fie că au sau nu un divizor comun.
În concluzie, analiză trebuie făcută prin egalitatea respectivă și nu separat, iar demonstrația autorului se rezumă la ceea ce nu poate implica și demonstra conjectura, oricât de corecte ar fi celelalte dezvoltări.
Cu alte cuvinte, nu poți demonstra o afirmație matematică prin ea însăși.
Trebuie să te folosești de ceva care să implice adevărul afirmației.
Este menționat un pic la început egalitatea ecuației, după care ceea ce este analizat în continuare nu mai are nicio treabă cu valorile a^x și b^y.
Este analizată strict, și izolat, doar valoarea c^z, valoare pentru care nu este menționată și implicată direct faptul că ea este suma a^x+b^y, ele putând fi orice fel de valori, pentru că nu mai sunt luate în calcul.
Situație în care nu implică în niciun fel adevărul conjecturii.
Nu există o relație directă care să implice egalitatea ecuației.
Peste tot pe unde a folosit c, ar fi trebuit să folosească suma respectivă, sub radical sau nu, să ajungă la concluzia că ele au un divizor comun. Dar iară nu e o implicație directă, pentru că poate alege oricare valori, fie că au sau nu un divizor comun.
În concluzie, analiză trebuie făcută prin egalitatea respectivă și nu separat, iar demonstrația autorului se rezumă la ceea ce nu poate implica și demonstra conjectura, oricât de corecte ar fi celelalte dezvoltări.
Cu alte cuvinte, nu poți demonstra o afirmație matematică prin ea însăși.
Trebuie să te folosești de ceva care să implice adevărul afirmației.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
curiosul a scris:În primul rând Geza, în demonstrația propriu zisă, este analizată doar valoarea c^z.
Corect!
Exact asta ii reproseaza si tipul din mesajul respectiv (printre multe altele) si intradevar pe buna dreptate
Ai reusit sa-ti dai seama de unde si pana unde formula aia (5) cu logaritmul ?
Vizitator- Vizitator
 Re: Conjectura Beal
Re: Conjectura Beal
Nu.Mezei Geza a scris:
Ai reusit sa-ti dai seama de unde si pana unde formula aia (5) cu logaritmul ?
Analizând-o, s-ar ajunge la exponentul ln(c)(z-1).
Dar...mister.
Tu cum crezi că a ajuns la acel exponent ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
De fapt, nu.
Exponentul ar fi o altă fracție.
Ia s-o mai analizez un pic.
Exponentul ar fi o altă fracție.
Ia s-o mai analizez un pic.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
De fapt, egalând exprimarea exponentului prin logaritmul natural în forma în care este cu numărul z, pentru că egalitatea ar trebui să fie adevărată, ea este falsă.
Dacă nu cumva îmi scapă ceva.
Dacă nu cumva îmi scapă ceva.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
În primul caz pe care l-a considerat, egalând valoarea exponenților se ajunge la :
}{ln(T)}-1&space;\right&space;)=\left&space;(&space;\frac{(z)ln(c)}{ln(T)}-1&space;\right&space;)})
Cam fals, după părerea mea.
Cam fals, după părerea mea.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
De fapt nu prea, pentru că el a ridicat la aceea putere și valoarea T de la numitor, aleasă arbitrar.
Se schimbă situația.
După cum e scris, valoarea c/T este toată ridicată la aceea putere.
Dar chiar și așa, dacă ridicăm la aceea putere separat, atât numărătorul, cât și numitorul,
ar trebui să obținem la numitor T și la numărător c^z,
deci putem egala valoarea aceea atât cu z, cât și cu 1 simultan.
Se schimbă situația.
După cum e scris, valoarea c/T este toată ridicată la aceea putere.
Dar chiar și așa, dacă ridicăm la aceea putere separat, atât numărătorul, cât și numitorul,
ar trebui să obținem la numitor T și la numărător c^z,
deci putem egala valoarea aceea atât cu z, cât și cu 1 simultan.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
În al doilea caz, cu z/2 , se vede că el ridică toată valoarea la acel exponent, iar așa se verifică și se înțelege că așa a vrut să procedeze și în primul caz, dar oricum, valoarea aceea trebuie și ne putem permite s-o egalăm cu z, în primul caz și cu z/2 în al doilea caz.
Greșesc Geza ?
Greșesc Geza ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
Ar trebui să luăm în calcul și ce spune autorul exact înainte :
and its newly discovered logarithmic
consequences are actually represented.
La ce fel de nouă descoperire se referă ?
and its newly discovered logarithmic
consequences are actually represented.
La ce fel de nouă descoperire se referă ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
Relatia ma depaseste cum ti-am spus.curiosul a scris:Ar trebui să luăm în calcul și ce spune autorul exact înainte :
and its newly discovered logarithmic
consequences are actually represented.
La ce fel de nouă descoperire se referă ?
Nu imi dau seama ce vrea sa fie zica,asa pentru orice valori ea este falsa speram sa fie ceva legat de numere prime sau ceva ce nu cunosc.
Nu mi-am batut capul cu ea si nici pe tine nu vad cu ce te-ar ajuta chiar daca este corecta si nu pricepem noi exact ce vrea sa zica
Vizitator- Vizitator
 Re: Conjectura Beal
Re: Conjectura Beal
Ai dreptate !
Trebuie s-o iau eu așa în stilul meu băbește, că înțeleg și mai bine ce fac.
Trebuie s-o iau eu așa în stilul meu băbește, că înțeleg și mai bine ce fac.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
Daca am gasii undeva expresia data de el demonstrata poate ar fi utila.
Dar asa pe "uscat" eu nu pricep ce face
Dar asa pe "uscat" eu nu pricep ce face
Vizitator- Vizitator
 Re: Conjectura Beal
Re: Conjectura Beal
Am găsit ceva undeva de unde reiese că el a egalat T cu c. Dar tot nu-i corect.
Oricum, la o căutare mai profundă, duduie internetul de demonstrații ale acestei conjecturi.
Una mai simplă ca alta.
Am ajuns la concluzia că există un raport direct proporțional între simplitatea demonstrației și a gândirii autorului.
 valabil și pentru mine
valabil și pentru mine 
Fără ceva nou, pur creativ, niciuna din infinitatea de demonstrații simple care există, nu va fi în veci validată sau recunoscută.
Mai ales pentru asemenea probleme.
Odată astea spuse, dacă e să mă raportez la mine însumi, eu pot doar să le analizez pentru a le înțelege mai bine, dar în niciun caz pentru a ajunge la o asemenea demonstrație, dacă e să fim realiști.
Asta e, măcar îmi ocup timpul cu ceva ce-mi place.
Oricum, la o căutare mai profundă, duduie internetul de demonstrații ale acestei conjecturi.
Una mai simplă ca alta.
Am ajuns la concluzia că există un raport direct proporțional între simplitatea demonstrației și a gândirii autorului.
Fără ceva nou, pur creativ, niciuna din infinitatea de demonstrații simple care există, nu va fi în veci validată sau recunoscută.
Mai ales pentru asemenea probleme.
Odată astea spuse, dacă e să mă raportez la mine însumi, eu pot doar să le analizez pentru a le înțelege mai bine, dar în niciun caz pentru a ajunge la o asemenea demonstrație, dacă e să fim realiști.
Asta e, măcar îmi ocup timpul cu ceva ce-mi place.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
curiosul a scris:
Fără ceva nou, pur creativ, niciuna din infinitatea de demonstrații simple care există, nu va fi în veci validată sau recunoscută.
Mai ales pentru asemenea probleme.
Asta e, măcar îmi ocup timpul cu ceva ce-mi place.
Perfect deacord !
Este f complexa problema.Incearca eventual doar pentru cazuri particulare:
x=2,y=2,z=3
Vizitator- Vizitator
 Re: Conjectura Beal
Re: Conjectura Beal
Geza, sau oricine altcineva,
cum credeți că am putea demonstra faptul că, oricare ar fi numerele naturale
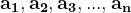
dacă ele nu au toate un divizor comun, atunci fracția de mai jos este ireductibilă :
^2+(a_2)^2+(a_3)^2+...+(a_n)^2}{a_1+a_2+a_3+...+a_n}})
Sau cel puțin, ce condiții ar trebui îndeplinite ca fracția de mai sus să fie una ireductibilă ?
Este suficientă cea menționată, adică să nu aibă toate un divizor comun ?
Vă mulțumesc pentru vreo idee măcar.
cum credeți că am putea demonstra faptul că, oricare ar fi numerele naturale
dacă ele nu au toate un divizor comun, atunci fracția de mai jos este ireductibilă :
Sau cel puțin, ce condiții ar trebui îndeplinite ca fracția de mai sus să fie una ireductibilă ?
Este suficientă cea menționată, adică să nu aibă toate un divizor comun ?
Vă mulțumesc pentru vreo idee măcar.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
O singura idee imi trece prin cap dar nu este rumegata
ai incercat sa-l scrii pe
a1^2+a2^2+a3^2+...=
(a1+a2++a3)^2-2(+a1a2+a1a3+...a2a3+...)
si sa intorci a doua fractie ?
ai incercat sa-l scrii pe
a1^2+a2^2+a3^2+...=
(a1+a2++a3)^2-2(+a1a2+a1a3+...a2a3+...)
si sa intorci a doua fractie ?
Vizitator- Vizitator
 Re: Conjectura Beal
Re: Conjectura Beal
Nu, dar mi se pare o idee bună.Mezei Geza a scris:O singura idee imi trece prin cap dar nu este rumegata
ai incercat sa-l scrii pe
a1^2+a2^2+a3^2+...=
(a1+a2++a3)^2-2(+a1a2+a1a3+...a2a3+...)
si sa intorci a doua fractie ?
Mersi mult.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
Chiar acuma iti scriam ca nu prea vad cu ce te-ar putea ajuta.
Am facut cazul pe trei componente si nu vad sensul sa intorci fractia mai repede asa cum am scris-o in mesajul anterior s-ar putea sa te ajute
Am facut cazul pe trei componente si nu vad sensul sa intorci fractia mai repede asa cum am scris-o in mesajul anterior s-ar putea sa te ajute
Vizitator- Vizitator
 Re: Conjectura Beal
Re: Conjectura Beal
Ceva de genul:
(a^2+b^2+c^2)/(a+b+c)=
(a+b+c)-2(ab+ac+bc)/(a+b+c)=
(a+b+c)-2/((a+b+c)/(ab+ac+bc))
Acuma vad ca nu rezolvi mare lucru

(a^2+b^2+c^2)/(a+b+c)=
(a+b+c)-2(ab+ac+bc)/(a+b+c)=
(a+b+c)-2/((a+b+c)/(ab+ac+bc))
Acuma vad ca nu rezolvi mare lucru
Vizitator- Vizitator
 Re: Conjectura Beal
Re: Conjectura Beal
Și am să-ți arat Geza și la ce folosește.
Dacă nu mă pripesc în afirmație, teorema lui Fermat se poate demonstra extrem de simplu.
Și am reluat-o o idee gândindu-mă că dacă nu pot demonstra teorema lui Fermat, cu siguranță nu pot demonstra nici conjectura lui Beal.
Și cred că ceea ce ai scris tu este deja destul de folositor.
O să scriu mesajul din care rezultă asta în următoarele minute (sau zeci de minute, că e un pic de scris.)
Eventual să-mi spui părerea ta despre ce voi scrie.
Mie mi se pare destul de interesant și suficient de ingenios raționamentul, dar este nevoie de demonstrația afirmației de mai sus.
Sau poate că nu mai este necesară generalizarea ei prin fracția de mai sus, odată ce vezi la ce mă refer.
Ies la o țigară și după aia mă apuc de scris.
Cu siguranță o să ți se pară și ție destul de interesant.
Dacă nu mă pripesc în afirmație, teorema lui Fermat se poate demonstra extrem de simplu.
Și am reluat-o o idee gândindu-mă că dacă nu pot demonstra teorema lui Fermat, cu siguranță nu pot demonstra nici conjectura lui Beal.
Și cred că ceea ce ai scris tu este deja destul de folositor.
O să scriu mesajul din care rezultă asta în următoarele minute (sau zeci de minute, că e un pic de scris.)
Eventual să-mi spui părerea ta despre ce voi scrie.
Mie mi se pare destul de interesant și suficient de ingenios raționamentul, dar este nevoie de demonstrația afirmației de mai sus.
Sau poate că nu mai este necesară generalizarea ei prin fracția de mai sus, odată ce vezi la ce mă refer.
Ies la o țigară și după aia mă apuc de scris.
Cu siguranță o să ți se pară și ție destul de interesant.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
Mezei Geza a scris:Ceva de genul:
(a^2+b^2+c^2)/(a+b+c)=
(a+b+c)-2(ab+ac+bc)/(a+b+c)=
(a+b+c)-2/((a+b+c)/(ab+ac+bc))
Acuma vad ca nu rezolvi mare lucru
(a^2+b^2+c^2)/(a+b+c)=
(a+b+c)-2(ab+ac+bc)/(a+b+c)=
(a+b+c)-2(ab+ac+aa-aa+bc)/(a+b+c)=
(a+b+c)-2(ab+ac+aa)/(a+b+c)-2(-aa+bc)/(a+b+c)=
(a+b+c)-2a-2(-aa+bc)/(a+b+c)=
Vizitator- Vizitator
 Re: Conjectura Beal
Re: Conjectura Beal
Deci,
pentru teorema lui Fermat trebuie să demonstrăm că pentru n mai mare ca 2, ecuația nu are soluții întregi.
Scriem mai întâi x din ecuație sub forma :
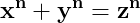
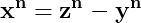
\left&space;\{&space;z^{n-1}+z^{n-2}y+...+zy^{n-2}+y^{n-1}&space;\right&space;\}})
Egalitate care ne este suficient de cunoscută amândurora pentru că am mai analizat-o în alt subiect amândoi.
Aduce ecuația inițială la o altă formă :
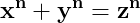
^2=\left&space;(z^n&space;\right&space;)^2})
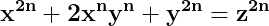
=z^{2n}-y^{2n}})
=\left&space;(z^2&space;\right&space;)^n-\left&space;(y^2&space;\right&space;)^n})
=\left&space;(&space;z^2-y^2&space;\right&space;)\left&space;\{&space;\left&space;(&space;z^2&space;\right&space;)^{n-1}+\left&space;(&space;z^2&space;\right&space;)^{n-2}y^2+...+z^2\left&space;(&space;y^2&space;\right&space;)^{n-2}+\left&space;(&space;y^2&space;\right&space;)^{n-1}&space;\right&space;\}})
Înlocuim în partea stângă valoarea lui x la puterea n obținută anterior și obținem :
\left&space;\{&space;z^{n-1}+z^{n-2}y+...+zy^{n-2}+y^{n-1}&space;\right&space;\}\left&space;(&space;x^n+2y^n&space;\right&space;)=})
\left&space;(&space;z+y&space;\right&space;)\left&space;\{&space;\left&space;(&space;z^{n-1}&space;\right&space;)^{2}+\left&space;(&space;z^{n-2}y&space;\right&space;)^{2}+...+\left&space;(z&space;y^{n-2}&space;\right&space;)^{2}+\left&space;(&space;y^{n-1}&space;\right&space;)^{2}&space;\right&space;\}})
Simplificăm prin z-y, iar acoladele celor doi termeni care rămân ar fi cumva numărătorul și numitorul fracției din mesajele anterioare despre care vorbeam. Dacă fracția este ireductibilă, atunci cele două acolade sunt numere prime între ele. În egalitatea de mai sus, dacă cele două acolade sunt numere prime între ele, înseamnă că doar celălalt factor al termenului din dreapta, adică z+x, se poate divide cu acolada termenului din stânga egalității, ceea ce înseamnă că :
\geq&space;\left&space;\{&space;z^{n-1}+z^{n-2}y+...+zy^{n-2}+y^{n-1}&space;\right&space;\}})
Evident, pentru n mai mare ca 2, inegalitatea de mai sus nu este posibilă.
Menționăm și faptul că z și y sunt prime între ele, deci în cele două acolade nu toți termenii se divid cu un același divizor.
Dar trebuie demonstrat că cele două acolade sunt numere prime între ele și nu au niciun divizor comun.
Putem alege convenabil una din valorile x sau y, pentru care putem aduce ecuația la exprimarea de mai sus ca să eliminăm situația în care 2 ar putea fi factorul comun al lor.
Ce zici Geza, cum ți se pare ?
pentru teorema lui Fermat trebuie să demonstrăm că pentru n mai mare ca 2, ecuația nu are soluții întregi.
Scriem mai întâi x din ecuație sub forma :
Egalitate care ne este suficient de cunoscută amândurora pentru că am mai analizat-o în alt subiect amândoi.
Aduce ecuația inițială la o altă formă :
Înlocuim în partea stângă valoarea lui x la puterea n obținută anterior și obținem :
Simplificăm prin z-y, iar acoladele celor doi termeni care rămân ar fi cumva numărătorul și numitorul fracției din mesajele anterioare despre care vorbeam. Dacă fracția este ireductibilă, atunci cele două acolade sunt numere prime între ele. În egalitatea de mai sus, dacă cele două acolade sunt numere prime între ele, înseamnă că doar celălalt factor al termenului din dreapta, adică z+x, se poate divide cu acolada termenului din stânga egalității, ceea ce înseamnă că :
Evident, pentru n mai mare ca 2, inegalitatea de mai sus nu este posibilă.
Menționăm și faptul că z și y sunt prime între ele, deci în cele două acolade nu toți termenii se divid cu un același divizor.
Dar trebuie demonstrat că cele două acolade sunt numere prime între ele și nu au niciun divizor comun.
Putem alege convenabil una din valorile x sau y, pentru care putem aduce ecuația la exprimarea de mai sus ca să eliminăm situația în care 2 ar putea fi factorul comun al lor.
Ce zici Geza, cum ți se pare ?
Ultima editare efectuata de catre curiosul in Joi 13 Iun 2013, 23:46, editata de 2 ori (Motiv : corectari si completari)
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
1 observatie
Este gresit scrisa egalitatea :"cunoscuta amandoura"
nu trebuie cu +-+-+ ?
Sau ma prostesc eu ?
Este gresit scrisa egalitatea :"cunoscuta amandoura"
nu trebuie cu +-+-+ ?
Sau ma prostesc eu ?
Vizitator- Vizitator
 Re: Conjectura Beal
Re: Conjectura Beal
Părerea mea este că este corect scris. În acoladă/e toate sunt cu plus, nu ?Mezei Geza a scris:1 observatie
Este gresit scrisa egalitatea :"cunoscuta amandoura"
nu trebuie cu +-+-+ ?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Conjectura Beal
Re: Conjectura Beal
curiosul a scris:Mezei Geza a scris:1 observatie
Este gresit scrisa egalitatea :"cunoscuta amandoura"
nu trebuie cu +-+-+ ?
Părerea mea este că este corect scris. În acoladă/e toate sunt cu plus, nu ?
Parca retin ca nu !
Numai daca este x^n+y^n atunci sunt toate cu plus.
verifica in mesajele tale anterioare
Ai dreptate sunt cu plus :)la + sunt cu minus
Ok ma uit acuma in continuare
Vizitator- Vizitator
 Re: Conjectura Beal
Re: Conjectura Beal
Dacă fracția este ireductibilă, atunci cele două acolade sunt numere prime între ele. În egalitatea de mai sus, dacă cele două acolade sunt numere prime între ele, înseamnă că doar celălalt factor al termenului din dreapta, adică z+x, se poate divide cu acolada termenului din stânga egalității, ceea ce înseamnă că
banuiesc ca z+y nu z+x dar si asa am nevoie de un pic de ajutor ca imi scapa ceva
Nu mai face gif din formule sa le pot copia
banuiesc ca z+y nu z+x dar si asa am nevoie de un pic de ajutor ca imi scapa ceva
Nu mai face gif din formule sa le pot copia
Vizitator- Vizitator
 Re: Conjectura Beal
Re: Conjectura Beal
Bun.
Într-adevăr, z+y, acum am văzut că nu este corectat.
În ce privește gif-ul, eu doar copii scriptul html de pe site-ul unde reproduc codul ecuațiilor.
Deci s-a ajuns la ultima egalitate, în care, deocamdată, presupunem că cele două acolade sunt numere prime între ele. Asta înseamnă că niciunul din divizorii uneia nu se găsește în factorizarea celeilalte.
Dar în termenul din dreapta, noi trebuie să avem toți divizorii din factorizarea termenului din stânga egalității, atât timp cât vorbim de o egalitate.
Dar termenul din dreapta este exprimat ca produs de doi factori în care unul din ei nu conține niciun divizor al acoladei din stânga egalității.
Asta înseamnă că toți divizorii acoladei din stânga trebuie să apară în factorizarea celuilalt factor al produsului din dreapta, adică z+y.
Dar am scris mai mare sau egal, pentru că nu rezultă de nicăieri deocamdată că z+y nu poate conține și alți divizori.
Ulterior, prin inegalitatea care apare, rezultă că pentru n mai mare ca 2 ea nu poate fi posibilă.
Înțelegi până aici ?
S-ar putea să fie cam greoaie exprimare mea, dar nu știu cum să mă exprim altfel.
Dacă vrei o luăm cu exemple numerice că e mai simplu.
Într-adevăr, z+y, acum am văzut că nu este corectat.
În ce privește gif-ul, eu doar copii scriptul html de pe site-ul unde reproduc codul ecuațiilor.
Deci s-a ajuns la ultima egalitate, în care, deocamdată, presupunem că cele două acolade sunt numere prime între ele. Asta înseamnă că niciunul din divizorii uneia nu se găsește în factorizarea celeilalte.
Dar în termenul din dreapta, noi trebuie să avem toți divizorii din factorizarea termenului din stânga egalității, atât timp cât vorbim de o egalitate.
Dar termenul din dreapta este exprimat ca produs de doi factori în care unul din ei nu conține niciun divizor al acoladei din stânga egalității.
Asta înseamnă că toți divizorii acoladei din stânga trebuie să apară în factorizarea celuilalt factor al produsului din dreapta, adică z+y.
Dar am scris mai mare sau egal, pentru că nu rezultă de nicăieri deocamdată că z+y nu poate conține și alți divizori.
Ulterior, prin inegalitatea care apare, rezultă că pentru n mai mare ca 2 ea nu poate fi posibilă.
Înțelegi până aici ?
S-ar putea să fie cam greoaie exprimare mea, dar nu știu cum să mă exprim altfel.
Dacă vrei o luăm cu exemple numerice că e mai simplu.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
Pagina 2 din 3 •  1, 2, 3
1, 2, 3 
Pagina 2 din 3
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 