Conjectura Beal

Scris de **curiosul** Sam 08 Iun 2013, 18:46

Rezumarea primului mesaj :

Enunțul acestei conjecturi afirmă faptul că ecuația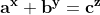 $\mathbf{a^x+b^y=c^z}$ are soluții pentru x, y, z mai mari ca 2, doar dacă a, b, c au un divizor comun.

Să încercăm să dezvoltăm în acest subiect modalități de demonstrare a acestei conjecturi.

În primul rând, ceea ce este evident și rezultă direct este faptul că dacă această ecuație are soluții care nu sunt prime între ele, deci au un divizor comun, atunci prin simplificare cu acel divizor, ecuația ajunge să aibă și soluții prime între ele, pentru acele valori x, y, z.
Deci ar trebui analizate soluțiile primitive ale ecuației.

Problema care se ridică în această situație este alta.
Este suficient să demonstrăm că ecuația nu are soluții primitive, pentru ca să rezulte că dacă ea are soluții, atunci acestea nu sunt prime între ele ?
Pentru că aceasta cere de fapt enunțul conjecturii.
Trebuie arătat că dacă ecuația are soluții, atunci soluțiile a, b, c au un divizor comun.
Din punctul meu de vedere, conjectura se rezumă doar la a demonstra că ecuația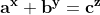 $\mathbf{a^x+b^y=c^z}$ nu are soluții a, b, c prime între ele.
Dacă nu are soluții primitive, atunci fie ecuația nu are soluții, fie ecuația are soluții a, b, c, dar acestea nu sunt prime între ele, ci au un divizor comun.

Dar apare imposibilitatea prin faptul că dacă ecuația are soluții a, b, c care au un divizor comun, atunci are și soluții prime între ele.

Cu alte cuvinte, demonstrația este făcută doar prin menționarea aspectului de mai sus.
Dacă ecuația are soluții, are obligatoriu soluții prime între ele.
Așa cum rezultă din raționamentul de mai jos :

Considerăm x, y, z diferite, fără să aibă importanță care dintre ele este mai mare ca oricare alta.
Considerăm numărul p divizorul comun al acestora.
Ecuația devine :

$\dpi{150} \begin{cases} \mathbf{a^x+b^y=c^z}\\ \mathbf{a=p{a}'} \\ \mathbf{b=p{b}'} \\ \mathbf{c=p{c}'} \\ \mathbf{x\leq y\leq z} \end{cases}\Rightarrow \mathbf{(p{a}')^x+(p{b}')^y=(p{c}')^z}$

Simplificăm prin divizorul comun p la cea mai mică putere (presupunem că această putere este x prin condiția pusă (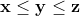 $\mathbf{x\leq y\leq z}$ ) iar ecuația devine :

$\dpi{150} \mathbf{({a}')^x+p^{y-x}({b}')^y=p^{z-x}({c}')^z}$

Ecuație care deasemenea poate fi scrisă

$\dpi{150} \mathbf{({a}')^x=p^{z-x}({c}')^z-p^{y-x}({b}')^y}$

Dacă z este mai mare ca y, de aici rezultă că în termenul din dreapta egalității mai poate fi scos factorul comun p , pentru că z-x>y-x :

$\dpi{150} \mathbf{({a}')^x=p^{y-x}[p^{z-y}({c}')^z-({b}')^y]}$

De aici rezultă că egalitatea de mai sus este adevărată doar dacă termenul din stânga se divide cu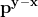 $\mathbf{p^{y-x}}$ .

Dar de asemenea rezultă că a' se divide cu p și nu numai, din egalitatea la care sa ajuns, rezultă că p trebuie să fie cel puțin la puterea x în factorizarea lui $\mathbf{({a}')^x}$ .
Din condiția pusă,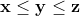 $\mathbf{x\leq y\leq z}$ , rezultă că

$\dpi{150} \mathbf{({a}')^x=p^{y-x}p^s({a}'')^x}$

unde y-x+s=x.

Înlocuind în ecuația la care s-a ajuns valoarea de mai sus, egalitatea devine :

$\dpi{150} \mathbf{({a}')^x=p^{y-x}[p^{z-y}({c}')^z-({b}')^y]}$

$\dpi{150} \mathbf{p^{y-x}p^s({a}'')^x=p^{y-x}[p^{z-y}({c}')^z-({b}')^y]}$

$\dpi{150} \mathbf{p^s({a}'')^x=p^{z-y}({c}')^z-({b}')^y}$

Egalitate pe care o putem aduce la forma

$\dpi{150} \mathbf{({b}')^y=p^{z-y}({c}')^z-p^s({a}'')^x}$

Din egalitatea de mai sus putem scoate în termenul din dreapta factorul comun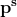 $\mathbf{p^s}$ iar egalitatea devine

$\dpi{150} \mathbf{({b}')^y=p^s[p^{z-y-s}({c}')^z-({a}'')^x]}$

de unde rezultă că b' trebuie să se dividă din nou cu p.

Se pare că am ajuns în situația anterioară și vom ajunge în aceeași situație ori de câte ori vom continua raționamentul pe același principiu.

Dar continuând în același mod raționamentul vom ajunge să arătăm că una din valorile a, b este exact divizorul comun al soluțiilor a, b, c.
Carevasăzică, forma ecuației inițiale, plecând de la presupunerea că soluțiile a, b, c au divizorul comun p, va deveni

$\dpi{150} \mathbf{a^x+(a\cdot b)^y=(a\cdot c)^z}$

Simplificând ecuația prin a la puterea x , aceasta devine

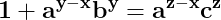
$\dpi{150} \mathbf{1+a^{y-x} b^y= a^{z-x}c^z}$

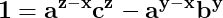
$\dpi{150} \mathbf{1= a^{z-x}c^z-a^{y-x} b^y}$

Dacă z este mai mare ca y, atunci în partea dreaptă a egalității îl putem scoate factor comun pe a, ceea ce ar însemna că 1 se divide cu a. Evident fals, dacă a este mai mare ca 1, egalitatea de mai sus neavând, de altfel, niciun fel de soluții netriviale.
Pentru că soluțiile triviale ale ecuației de mai sus sunt de altfel și soluțiile triviale ale ecuației inițiale, acestea ies din calcul.

În consecință, am arătat că plecând de la ipoteza că ecuația ar avea soluții a, b, c, având toate un divizor comun p, se ajunge la a arăta că ecuația nu are soluții.

Ecuația ar putea avea soluții dacă soluțiile a, b, c sunt soluții primitive și prime între ele.

Deci vis-a-vis de acestă conjectura am arătat exact inversul.
Ea poate avea soluții doar dacă a, b, c sunt prime între ele, nicidecum că ele trebuie să aibă proprietatea că au un divizor comun.

Ciudată întorsătură de situație.
Raționamentul prezentat mai sus este dezvoltat așa la repezeală și s-ar putea să nu fie corect, dar sper să dea idei și altora care știu cum să fructifice concluziile mele.

Aștept oricum, feedback-urile voastre, să vedem ce putem corecta.

Scris de Vizitator Vin 14 Iun 2013, 00:08

Dacă fracția este ireductibilă, atunci cele două acolade sunt numere prime între ele. În egalitatea de mai sus, dacă cele două acolade sunt numere prime între ele, înseamnă că doar celălalt factor al termenului din dreapta, adică z+x, se poate divide cu acolada termenului din stânga egalității, ceea ce înseamnă că

banuiesc ca z+y nu z+x dar si asa am nevoie de un pic de ajutor ca imi scapa ceva
Nu mai face gif din formule sa le pot copia

Scris de **curiosul** Vin 14 Iun 2013, 00:18

Bun.
Într-adevăr, z+y, acum am văzut că nu este corectat.
În ce privește gif-ul, eu doar copii scriptul html de pe site-ul unde reproduc codul ecuațiilor.

Deci s-a ajuns la ultima egalitate, în care, deocamdată, presupunem că cele două acolade sunt numere prime între ele. Asta înseamnă că niciunul din divizorii uneia nu se găsește în factorizarea celeilalte.
Dar în termenul din dreapta, noi trebuie să avem toți divizorii din factorizarea termenului din stânga egalității, atât timp cât vorbim de o egalitate.
Dar termenul din dreapta este exprimat ca produs de doi factori în care unul din ei nu conține niciun divizor al acoladei din stânga egalității.
Asta înseamnă că toți divizorii acoladei din stânga trebuie să apară în factorizarea celuilalt factor al produsului din dreapta, adică z+y.
Dar am scris mai mare sau egal, pentru că nu rezultă de nicăieri deocamdată că z+y nu poate conține și alți divizori.
Ulterior, prin inegalitatea care apare, rezultă că pentru n mai mare ca 2 ea nu poate fi posibilă.

Înțelegi până aici ?
S-ar putea să fie cam greoaie exprimare mea, dar nu știu cum să mă exprim altfel.
Dacă vrei o luăm cu exemple numerice că e mai simplu.

Scris de Vizitator Vin 14 Iun 2013, 00:30

Nu exprimarea ta este greoie,eu nu "le vad" asa repede cum le gandesti tu ca nu am lucrat cu ele niciodata.

Un exemplu numeric ar fi de real ajutor Very Happy

Scris de **curiosul** Vin 14 Iun 2013, 00:38

Ok.
Presupunem produsurile egalității:

(2*3*4*17){23*15*121}=(a*b*c){16*43*29}

Am încercat să reproduc structura egalității din analiză.
Cele două acolade sunt prime între ele, deci nu au niciun divizor comun.
Dar factorii din prima acoladă 23, 15, 121 trebuie să apară în termenul din dreapta.
Dar dacă ei nu apar în termenul din dreapta în acoladă, ei trebuie obligatoriu să apară în paranteza (a*b*c).
În cazul nostru, ce rămâne după simplificarea cu z-x în ambii termeni, adică exact z+y.
E mai bine ?

Dar ca să înțelegi și mai bine, egalitatea din exemplul de mai sus nu este posibilă, ea este pur exemplificativă, pentru simplul fapt că în dreapta apare factor 29, spre exemplu, iar în stânga nu apare.
Adică stabilim o egalitate între un număr care se divide cu 29 și unul care nu se divide cu 29.
Imposibil.

Scris de **curiosul** Vin 14 Iun 2013, 00:42

Dă un refresh că am mai corectat câte ceva.

Scris de **curiosul** Vin 14 Iun 2013, 00:53

Geza,
trebuie să plec și s-ar putea să nu-ți mai pot răspunde astăzi la întrebări.
Tu scrie tot ce vrei să întrebi și când voi reveni, le iau la rând pe toate și-ți răspund mâine, cât mă pricep de bine.
O seară bună.

Scris de Vizitator Vin 14 Iun 2013, 00:54

curiosul a scris:Ok.
Presupunem produsurile egalității:

(2*3*4*17){23*15*121}=(a*b*c){16*43*29}

Am încercat să reproduc structura egalității din analiză.
Cele două acolade sunt prime între ele, deci nu au niciun divizor comun.
Dar factorii din prima acoladă 23, 15, 121 trebuie să apară în termenul din dreapta.
Dar dacă ei nu apar în termenul din dreapta în acoladă, ei trebuie obligatoriu să apară în paranteza (a*b*c).
În cazul nostru, ce rămâne după simplificarea cu z-x în ambii termeni, adică exact z+y.
E mai bine ?

Dar ca să înțelegi și mai bine, egalitatea din exemplul de mai sus nu este posibilă, ea este pur exemplificativă, pentru simplul fapt că în dreapta apare factor 29, spre exemplu, iar în stânga nu apare.
Adică stabilim o egalitate între un număr care se divide cu 29 și unul care nu se divide cu 29.
Imposibil.

Vazi asta nu mi-a trecut prin cap

43 si 16-le nu este in aceasi situatie ca si 29 ?

Noapte Buna

Scris de **curiosul** Vin 14 Iun 2013, 12:12

Mezei Geza a scris:43 si 16-le nu este in aceasi situatie ca si 29 ?

Ba da.
Problema este că raționamentul nu este valid.
Acolada din dreapta, în cazul nostru, este multiplul celeilalte.
Este totuși interesant de analizat cealaltă observație.

Scris de Vizitator Vin 14 Iun 2013, 12:48

"Este totuși interesant de analizat cealaltă observație."

Inegalitatea respectiva mie tot nu imi este clara,este gresita?
Care cealalta observatie?

Scris de **curiosul** Vin 14 Iun 2013, 18:20

La aceasta mă refer că nu e validă:

curiosul a scris: $\mathbf{(z-y)\left \{ z^{n-1}+z^{n-2}y+...+zy^{n-2}+y^{n-1} \right \}\left ( x^n+2y^n \right )=}$

$\mathbf{=\left ( z-y \right )\left ( z+y \right )\left \{ \left ( z^{n-1} \right )^{2}+\left ( z^{n-2}y \right )^{2}+...+\left (z y^{n-2} \right )^{2}+\left ( y^{n-1} \right )^{2} \right \}}$

Acolada de jos (adică din dreapta egalității) este multiplul celei de sus (adică din stânga egalității).
Deci cele două acolade nu sunt prime între ele.
Raționamentul care ar fi demonstrat teorema ar fi fost valid doar prin această condiție, care nu este îndeplinită.

Cealaltă observație este asta :

curiosul a scris:oricare ar fi numerele naturale
$\mathbf{a_1,a_2,a_3,...,a_n}$
dacă ele nu au toate un divizor comun, atunci fracția de mai jos este ireductibilă :

$\mathbf{\frac{(a_1)^2+(a_2)^2+(a_3)^2+...+(a_n)^2}{a_1+a_2+a_3+...+a_n}}$

Sau cel puțin, ce condiții ar trebui îndeplinite ca fracția de mai sus să fie una ireductibilă ?

Aici aș mai completa că numerele respective sunt prime între ele.
Sau cum ar fi dacă am ridica la puterea n termenii numărătorului ?
Și desigur, putem extinde foarte mult.

Oricum, am mai analizat astăzi o idee teorema lui Fermat și se pare că pentru n par se poate demonstra.
O să ți-o arat mai târziu.
O mai verific un pic și dacă mai ai dispoziție o să discutăm pe marginea ei.

Scris de **curiosul** Sam 15 Iun 2013, 09:27

Geza,
analizând ecuația $\mathbf{x^{2k}+y^{2k}=z^{2k}}$ pot să demonstrez că soluțiile x, y, z ale ecuației din egalitate pot fi scrise în felul următor :

$\mathbf{x^{2k}+y^{2k}=z^{2k}}\Rightarrow \begin{cases} \mathbf{x^k=\left (\frac{u^{2k}-v^{2k}}{2}} \right ) \\ \mathbf{y^k=u^kv^k} \\ \mathbf{z^k=\left (\frac{u^{2k}+v^{2k}}{2}} \right ) \\ \end{cases}$

În cazul n=2, soluțiile sunt

$\mathbf{x^{2}+y^{2}=z^{2}}\Rightarrow \begin{cases} \mathbf{x=\left (\frac{u^{2}-v^{2}}{2}} \right ) \\ \mathbf{y=uv} \\ \mathbf{z=\left (\frac{u^{2}+v^{2}}{2}} \right ) \\ \end{cases}$

În încercarea de a demonstra cazul n număr par generalizat, am plecat folosind raționamentul următor :

Dacă k este mai mare ca 1 și presupunem că

$\mathbf{x^k=\left (\frac{u^{2k}-v^{2k}}{2} \right )}\Rightarrow \mathbf{x}=\sqrt[\mathbf{k}]{\mathbf{\frac{u^{2k}-v^{2k}}{2}}}$

este un număr întreg, atunci

$\mathbf{z^k=\left (\frac{u^{2k}+v^{2k}}{2} \right )}\Rightarrow \mathbf{z}=\sqrt[\mathbf{k}]{\mathbf{\frac{u^{2k}+v^{2k}}{2}}}$

nu mai este un număr întreg.
Menționez și faptul că u, v trebuie să fie prime între ele, dacă x, y, z sunt prime între ele.
aceasta se poate demonstra plecând de la faptul că una din valorile x sau y este obligatoriu impară, dacă x, y, z sunt prime dintre ele.
Am ales-o pe cea impară, în cazul nostru după cum sunt dezvoltate soluțiile , y este soluția impară și pot să arăt că u și v sunt prime între ele, dacă x, y, z sunt prime între ele.

Dar este o mică greșeală undeva pe care nu o pot corecta deocamdată.
Ai vreo idee, plecând de la modul în care sunt dezvoltate soluțiile.
Mă ocup eu de demonstrarea faptului că doar acelea pot fi soluțiile, adică

$\mathbf{x^{2k}+y^{2k}=z^{2k}}\Rightarrow \begin{cases} \mathbf{x^k=\left (\frac{u^{2k}-v^{2k}}{2}} \right ) \\ \mathbf{y^k=u^kv^k} \\ \mathbf{z^k=\left (\frac{u^{2k}+v^{2k}}{2}} \right ) \\ \end{cases}$

Ai vreo idee ?

Scris de Vizitator Sam 15 Iun 2013, 13:25

Din pacate nu am.
O sa dispar o vreme dar saptamana viitoare revin.
Incearca pana atunci sa-ti aduni calculele si sa si sintetizezi cateva "idei" care sigur sunt corecte.
Ne auzim ! (sau mai exact ne scriem)

Scris de **curiosul** Sam 15 Iun 2013, 18:09

Mezei Geza a scris:
Incearca pana atunci sa-ti aduni calculele si sa si sintetizezi cateva "idei" care sigur sunt corecte.

Ok.
Ca să nu încărcăm nici forumul, nici mintea celorlalți cu informații inutile, o să încerc să mă rezum doar la a expune ideile certe, iar când revii și vrei, mai discutăm despre ele.
Și aș începe cu demonstrația modului în care pot fi exprimate soluțiile x, y, și z din mesajul anterior.

Plecăm de la faptul că soluțiile x, y și z ale ecuației $\mathbf{x^{2k}+y^{2k}=z^{2k}}$ sunt prime între ele, deci nu există un divizor comun care să le dividă pe toate.
În caz contrar, dacă cel puțin două ar avea un divizor comun, va rezulta că toate trei trebuie să aibă acel divizor.
Prin simplificarea, ori de câte ori este necesar, cu divizorul lor comun se ajunge la soluții prime între ele, care satisfac egalitatea.
Așadar, considerăm x, y, z prime între ele.

În egalitatea $\mathbf{x^{2k}+y^{2k}=z^{2k}}$ , cel puțin una din soluțiile x sau y este o soluție impară. Dacă ambele soluții x și y ar fi pare, ar însemna că și z este un număr par, prin urmare x, y, z l-ar avea toate pe 2 ca și divizor comun.
Imposibil prin condiția prime între ele.
Presupunem în continuare că soluția y este soluția impară.
Raționamentul este identic și dacă am presupune x soluția impară.
Separând soluția impară, y în cazul nostru, obținem :

$\mathbf{y^{2k}=z^{2k}-x^{2k}=\left ( z^k-x^k \right )\left ( z^k+x^k \right )}$

Dacă y este impar, rezultă că numerele $\mathbf{\left (z^k-x^k \right )}$ și $\mathbf{\left (z^k+x^k \right )}$ sunt ambele impare.
Prin condiția x, y, z soluții prime între ele, deci și x , z prime între ele, rezultă că numerele $\mathbf{\left (z^k-x^k \right )}$ și $\mathbf{\left (z^k+x^k \right )}$ sunt prime între ele. Putem demonstra acest lucru presupunând că numerele $\mathbf{\left (z^k-x^k \right )}$ și $\mathbf{\left (z^k+x^k \right )}$ au un divizor comun q, iar într-un final dacă acestea au un același divizor, atunci atât z, cât și x, au același divizor. Pentru că z și x sunt prime între ele, ele nu pot avea un divizor comun, deci presupunerea făcută este falsă, iar numerele $\mathbf{\left (z^k-x^k \right )}$ și $\mathbf{\left (z^k+x^k \right )}$ sunt prime între ele.
Dacă acestea sunt prime între ele, rezultă că

$\begin{cases} \mathbf{z^k-x^k=u^{2k}}\\ \mathbf{z^k+x^k=v^{2k}}\\ \mathbf{y^{2k}=\left ( z^k-x^k \right )\left ( z^k+x^k \right )=\left ( u^kv^k \right )^2} \end{cases}$

Am ales soluția sigur impară, pentru că în cazul celălalt, cele două paranteze l-ar fi putut avea pe 2 factor comun,
iar în acest fel, pentru că z este impar, soluțiile u, v sunt impare și prime între ele.
Deci soluția y este produsul uv, deci poate fi întreg cu u, v naturale, dar ceea ce ne ajută,
după cum vom vedea în continuare,
este exprimarea $\mathbf{y^k=u^kv^k}$ .

Egalitatea inițială poate fi scrisă și după cum este dezvoltat mai jos :

$\mathbf{x^{2k}+y^{2k}=z^{2k}}$

$\mathbf{\left (x^k+y^k \right )^2-2x^ky^k=z^{2k}}$

$\mathbf{\left (x^k+y^k \right )^2-z^{2k}=2x^ky^k}$

$\mathbf{\left (x^k+y^k -z^k \right )\left ( x^k+y^k+z^k \right )=2x^ky^k}$

$\mathbf{\left [y^k -\left (z^k-x^k \right ) \right ]\left [y^k+\left (z^k+x^k \right ) \right ]=2x^ky^k}$

În egalitatea de mai sus, putem înlocui peste tot, cu excepția lui x la puterea k din dreapta, soluțiile u și v :
$\begin{cases} \mathbf{z^k-x^k=u^{2k}} \\ \mathbf{z^k+x^k=v^{2k}} \\ \mathbf{y^k=u^kv^k} \end{cases}$

$\mathbf{\left (u^kv^k -u^{2k} \right )\left ( u^kv^k+v^{2k} \right )=2x^ku^kv^k}$

$\mathbf{u^k\left (v^k -u^{k} \right )v^k\left ( u^k+v^k \right )=2x^ku^kv^k}$

$\mathbf{\left (v^k -u^{k} \right )\left ( u^k+v^k \right )=2x^k}$

$\mathbf{v^{2k}-u^{2k}=2x^k}$

Deci soluțiile x și y din ecuația $\mathbf{x^{2k}+y^{2k}=z^{2k}}$ sunt

$\mathbf{\left (x=\sqrt[\mathbf{k}]{\mathbf{\frac{v^{2k}-u^{2k}}{2}}}} \right ),\mathbf{\left (y=u\cdot v \right )}$

Înlocuind aceste valori în ecuație, putem obține și soluția z :

$\mathbf{\left (x=\sqrt[\mathbf{k}]{\mathbf{\frac{v^{2k}-u^{2k}}{2}}}} \right ),\mathbf{\left (y=u\cdot v \right ),\left (z=\sqrt[\mathbf{k}]{\mathbf{\frac{v^{2k}+u^{2k}}{2}}}} \right )$

Dacă considerăm u, v întregi, pentru cazul n număr par, soluția y este întreagă.
Ar trebui în continuare arătat că cel puțin unul din cele două rădăcini de ordin k nu poate fi întreg.

Scris de **curiosul** Sam 15 Iun 2013, 18:33

Abel, sau Răzvan, înlocuiți vă rog sistemul de mai jos:

$\begin{cases} \mathbf{z^k-x^k=u^{2k}} \\ \mathbf{z^k+x^k=v^{2k}} \\ \mathbf{y^k=u^kv^k} \end{cases}$

cu locul în scrie ecuație invalidă în mesajul anterior.
Nu l-am mai putut edita.
Mulțumesc.

S-a rezolvat.

Scris de **curiosul** Sam 15 Iun 2013, 19:31

[Offtopic]{Mulțumesc pentru corectare, Abel.}[/Offtopic]

Plecând de la soluțiile ecuației găsite în mesajul anterior:

$\begin{cases} \mathbf{x}=\left ( \sqrt[\mathbf{k}]{\mathbf{\frac{v^{2k}-u^{2k}}{2}}} \right )\\ \mathbf{y=\left (v\cdot u \right )} \\ \mathbf{z}=\left ( \sqrt[\mathbf{k}]{\mathbf{\frac{v^{2k}+u^{2k}}{2}}} \right ) \end{cases}$

putem stabili că dacă y este soluția impară, atunci x este cu certitudine soluția pară.
Dezvoltând ecuația inițială se ajunge la egalitatea:

$\mathbf{\left ( x^k+y^k-z^k \right )\left ( x^k+y^k+z^k \right )=2x^ky^k}$

Dacă am presupune că soluția x este la rândul ei impară, pentru că și y este impar, în partea din dreapta egalității apare factorul 2 doar la puterea întâi, pentru că indiferent de puterile lui x și y, dacă acestea sunt impare, puterile lor sunt impare.
Dacă x și y ar fi ambele impare, din suma a două numere impare rezultă un număr par, ceea ce înseamnă că z este par.
Dacă z este par, x și y impare, cele două paranteze ale termenului din stânga egalității :

$\mathbf{\left ( x^k+y^k-z^k \right )\left ( x^k+y^k+z^k \right )=2x^ky^k}$

sunt numere pare, de unde rezultă că produsul lor îl conține cel puțin pe 2 la puterea a doua, iar în partea dreaptă a egalității, dacă x și y sunt ambele impare, apare doar 2 la puterea întâi.
În felul acesta egalitatea este imposibilă, deci una din soluțiile x sau y este un număr par.
Dacă am considerat y soluția impară, atunci x este soluția pară.
Aceasta este :

$\mathbf{x}=\left ( \sqrt[\mathbf{k}]{\mathbf{\frac{v^{2k}-u^{2k}}{2}}} \right )\\$

iar dacă ea este pară și trebuie să fie întreagă, rezultă că

$\mathbf{v^{2k}-u^{2k}=s^k\cdot 2^{nk+1}}$

ajungându-se altfel la :

$\mathbf{x=\sqrt[\mathbf{k}]{\mathbf{\frac{s^k\cdot 2^{nk+1}}{2}}}=2^ns}$

unde n poate fi mai mare egal cu 1.

Dar analizând egalitatea

$\mathbf{v^{2k}-u^{2k}=s^k\cdot 2^{nk+1}}$

ea poate fi scrisă :

$\mathbf{\left (v^k \right )^2-\left (u^k \right )^2=s^k\cdot 2^{nk+1}}$

egalitate care se pare că este imposibilă adusă în congruență mod 4,
dacă u și v sunt prime între ele.
Dar să nu scriu prostii, trebuie să mai verific un pic.

Scris de **curiosul** Dum 16 Iun 2013, 14:49

Geza, când revii, dă-mi un semn !
O să-ți arăt o chestie foarte, foarte interesantă vis-a-vis de conjectura lui Beal. Cu siguranță o să înțelegi ce vreau să spun !

Scris de **curiosul** Vin 05 Iul 2013, 16:42

Geza,
cum am putea demonstra că dacă $\mathbf{a+b^n}$ se divide cu s, atunci $\mathbf{a+b^{n+(s-1)}}$ se divide de asemenea cu s ?

Și dacă ai și vreo idee pentru a demonstra că numerele (a+b) și (a+bc), cu a, b, c prime între ele,nenule, diferite, au în descompunerea lor factori primi diferiți.
a+b are cel puțin un factor prim pe care nu-l are a+bc,
iar a+bc are cel puțin un factor prim pe care nu-l are a+b.
Adică, nu există a, b, c naturale, nenule, diferite, astfel încât (a+b) și (a+bc) au aceeași factori primi, chiar dacă sunt la puteri diferite.

Ai vreo idee ?

Scris de **curiosul** Vin 05 Iul 2013, 19:11

Aprofundând cercetările vis-a-vis de conjectura lui Beal, există de asemenea o legătură interesantă cu faptul că $\mathbf{a^n\equiv (n+1)(\mathit{mod}n)}$ doar dacă a=(n+1).
Dar este destul de important să putem demonstra mai întâi că

curiosul a scris:Geza,
cum am putea demonstra că dacă $\mathbf{a+b^n}$ se divide cu s, atunci $\mathbf{a+b^{n+(s-1)}}$ se divide de asemenea cu s ?

Evident, putem considera și n=1, caz în care este valabil și ridicând la puterea s-1 cealaltă valoare, a.

Scris de Vizitator Vin 05 Iul 2013, 19:17

curiosul a scris:Geza,
cum am putea demonstra că dacă $\mathbf{a+b^n}$ se divide cu s, atunci $\mathbf{a+b^{n+(s-1)}}$ se divide de asemenea cu s ?

Și dacă ai și vreo idee pentru a demonstra că numerele (a+b) și (a+bc), cu a, b, c prime între ele,nenule, diferite, au în descompunerea lor factori primi diferiți.
a+b are cel puțin un factor prim pe care nu-l are a+bc,
iar a+bc are cel puțin un factor prim pe care nu-l are a+b.
Adică, nu există a, b, c naturale, nenule, diferite, astfel încât (a+b) și (a+bc) au aceeași factori primi, chiar dacă sunt la puteri diferite.

Ai vreo idee ?

Nu putem demonstra ca nu corect pentru orice a,b,n,s
Am dat un exemplu numeric si infirma ipoteza
a=7
b=3
n=4
a+b^n=7+3^4=7+81=88
88 se divide cu 2,4,8,11

a-Pentru s=2
a+b^{n+(s-1))=a+b^(n+1)=7+3^5=7+243=250
250 se divide cu 2,5,10,25,50.125
Este corect

b-Pentru s=11
a+b^{n+(s-1))=a+b^(4+10)=7+3^14=4782976
4782976 se divide cu 11
Este corect

c- Pentru s=8 avem problerme
a+b^{n+(s-1))=a+b^(4+7)=7+3^11=177154
Nu se divide cu 8
177154/8=22144.25

d-Pentru s=4 avem problerme
a+b^{n+(s-1))=a+b^(4+3)=7+3^7=2194
Nu se divide cu 4

Ma mai gandesc si iti spun,exista niste conditii suplimentare,nu merge asa pe general

Scris de **curiosul** Vin 05 Iul 2013, 20:44

Da, de aia îmi era greu să demonstrez cazul general.
Și eu am verificat o multe exemple, dar nu le-am analizat pentru fiecare divizor în parte, ci le-am ales aleatoriu.
O să trebuiască să mai verific și eu.

Iar aici

curiosul a scris:Aprofundând cercetările vis-a-vis de conjectura lui Beal, există de asemenea o legătură interesantă cu faptul că $\mathbf{a^n\equiv (n+1)(\mathit{mod}n)}$ doar dacă a=(n+1)

mai trebuia menționat pentru n impar.
Dar cred că și aici există contraexemple.
Oricum, mulțumesc pentru intervenție.
Mai verific și eu în continuare.

Scris de Vizitator Vin 05 Iul 2013, 20:50

Hai ca cred ca am gasit ceva conditii
Procedand similar ca si la impartirea polinoamelor am obtinut:
http://www.wolframalpha.com/input/?i=x%2By^%28n%2Bk%29%3Dy^k*%28x%2By^n%29-x%28y^k-1%29

am folosit alte notatii
din egaliatea de mai sus se poate deduce usor ca daca
x+Y^n este multiplu de c
x+Y^(n+k) este multiplu de c numai si numai daca:
ori x este un multiplu de c
ori y-1 este un multiplu de c (pe baza unei formule scrise mai demult de tine y^n-1^n=( y-1)(.....) )
Sper ca este corect si sa te ajute la ceva Smile

Daca este ceva neclar sa-mi spui

Scris de **curiosul** Vin 05 Iul 2013, 21:08

Da, destul de util.
Dacă k+1 este prim, iar x+y^n se divide cu k+1, prin mica teoremă a lui Fermat rezultă sigur că x+y^(n+k) se divide cu k+1, din exprimarea la care ai ajuns, dacă y nu se divide cu k+1, pentru că (y^k)-1 se divide cu k+1 dacă k+1 este prim.
Găsisem la un moment dat o exprimare asemănătoare în diferența sau suma a două puteri diferite.
Să vedem cum o putem folosi.
Îi găsesc eu o utilitate într-un fel sau altul.

Scris de **curiosul** Vin 05 Iul 2013, 21:13

Iar vis-a-vis de ipoteza enunțată anterior, prin exprimarea la care ai adus această ipoteză pentru s prim este validă.
Dacă s este prim, iar x+(y^n) se divide cu s, atunci x+[y^(n+s-1)] se divide cu s. condiția este ca fie x se divide cu s, fie y nu se divide cu s prim.
Raționamentul care o demonstrează este cel din mesajul anterior.
Oricum, bună și utilă exprimarea.

Scris de Vizitator Vin 05 Iul 2013, 21:18

curiosul a scris:Iar vis-a-vis de ipoteza enunțată anterior, prin exprimarea la care ai adus această ipoteză pentru s prim este validă.
Dacă s este prim, iar x+(y^n) se divide cu s, atunci x+[y^(n+s-1)] se divide cu s. condiția este ca fie x se divide cu s, fie y nu se divide cu s prim.
Raționamentul care o demonstrează este cel din mesajul anterior.
Oricum, bună și utilă exprimarea.

Tot cu impartirea polinoamelor am gandit-o
Vezi si forma asta:
http://www.wolframalpha.com/input/?i=%28x%2By^%28n%2Bk%29%29%2F%28x%2By^n%29%3Dy^k-x%28y^k-1%29%2F%28x%2By^n%29

Scris de **curiosul** Vin 05 Iul 2013, 23:21

Si se pare ca ma ajuta exprimarea ta.
Cel putin in ceea ce priveste demonstrarea cazului n=3 a teoremei lui Fermat.
Aceasta este urmatoarea:

Una din solutiile x, y sau z ale ecuatiei $\mathbf{x^3+y^3=z^3}$ se divide obligatoriu cu 3, dupa cum rezulta de mai jos.
Solutiile x, y, z ale ecuatiei satisfac conditia (x+y)>z. Daca sensul inegalitatii ar fi invers ar insemna ca $\mathbf{x^3+y^3<(x+y)^3\leq z^3}$ . Deci (x+y)>z. Asta inseamna ca putem scrie una din solutii, z spre exemplu, ca fiind x+y-k=z.
Rescriem ecuatia inlocuind valoarea lui z :

$\mathbf{x^3+y^3=(x+y-k)^3}$

$\mathbf{(x+y)(x^2-xy+y^2)=(x+y)^3-3(x+y)^2k+3(x+y)k^2-k^3}$

$\mathbf{(x+y)\left [ (x+y)^2-3xy \right ]=(x+y)^3-3(x+y)^2k+3(x+y)k^2-k^3}$

$\mathbf{(x+y)^3-3xy(x+y)=(x+y)^3-3(x+y)^2k+3(x+y)k^2-k^3}$

Simplificam cu x+y la puterea a treia si izolam k la puterea a treia :

$\mathbf{k^3=3xy(x+y)-3(x+y)^2k+3(x+y)k^2}$

$\mathbf{k^3=3(x+y)(xy-k(x+y)+k^2)}$

Observam ca trei apare factor al lui k, dar acesta, adica 3, trebuie sa apara in descompunerea lui k la puterea a treia, cel putin la puterea a treia, insa din forma in care este adusa ecuatia, aceasta il contine ca factor "vizibil" doar pe trei la puterea intai. De undeva trebuie sa-l mai obtinem, cel putin la puterea a doua, astfel incat prin produsul lor sa-l avem cel putin la puterea a treia.
Din forma in care este adusa egalitatea aceasta este posibila, daca cel putin una din cantitatile x+y, x sau y se divide cu trei.
x+y este unul din divizorii lui z la a treia, ceea ce inseamna ca daca x+y se divide cu 3, atunci obligatoriu z se divide cu trei, in consecinta, cel putin una din valorile x, y, z se divide cu 3.

Vom arata in continuare ca aceasta, solutia divizibila cu 3 poate fi doar z.

Daca x si y sunt nenule, atunci z este atat mai mare ca x, cat si mai mare ca y. Scriem solutia z ca fiind x+q si respectiv y+k.
Ecuatia devine:

$\mathbf{x^3+y^3=(y+k)^3}$

$\mathbf{x^3=(y+k)^3-y^3}$

$\mathbf{x^3=(y+k-y)\left [ (y+k)^2+y(y+k)+y^2 \right ]}$

$\mathbf{x^3=k(y^2+2ky+k^2+y^2+ky+y^2)}$

$\mathbf{x^3=k(3y^2+3ky+k^2)}$

Si aici aplicam rationamentul anterior. Daca consideram x solutia care se divide cu 3, din exprimarea de mai sus rezulta ca k se divide cu 3 obligatoriu. Dar in factorizarea lui x la puterea a treia, 3 trebuie sa apara la puterea a treia. Din modul in care este exprimata egalitatea de mai sus, 3 poate aparea la puterea a treia doar daca y se divide cu 3. Asta ar insemna ca atat x, cat si y se divid cu trei. Situatie imposibila prin conditia x, y, z prime intre ele, pentru ca ecuatia trebuie sa aiba si solutii primitive.
La fel procedam si in cazul in care inlocuim z=x+q si se ajunge in aceeasi situatie.

Deci x si y nu se divid cu 3. Pentru ca una din solutiile x, y, z se divide obligatoriu cu 3, aceea este solutia z si implicit x+y se divide cu 3, pentru ca ecuatia poate fi adusa la forma

$\mathbf{z^3=(x+y)\left [ (x+y)^2-3xy \right ]}$

iar z se divide cu 3 doar daca x+y se divide cu 3.

Asta inseamna ca $\mathbf{x^3+y^3}$ se divide cu 3.

Din egalitatea pe care ai exprimat-o tu anterior, analizand in sens invers, rezulta ca $\mathbf{x^3+y }$ se divide de asemenea cu 3.

Prin mica teorema a lui Fermat rezulta ca $\mathbf{x^3-x}$ se divide de asemenea cu 3.

Deci avem congruentele modulo 3,

$\begin{cases} \mathbf{x^3\equiv x} \\ \mathbf{x^3\equiv -y} \end{cases}mod3$

Ambele congruente sunt posibile doar daca y-x se divide cu 3. Dar avem de asemenea y+x divizibil cu 3, pentru ca z se divide cu 3.
Daca atat y-x, cat si y+x se divid cu 3, atunci ambele solutii, x si y, se divid cu 3.
Pentru ca si z se divide cu 3, inseamna ca ecuatia are solutii pentru n=3, doar daca toate solutiile se divid cu 3.
Imposibil pentru ca ecuatia trebuie sa aiba solutii primitive.
Daca demonstratia de mai sus este corecta si poate fi extinsa pentru orice n=p, p prim impar, rationamentul folosit sustine conjectura Beal.
Desigur, este posibil sa fie strecurata vreo greseala care imi scapa acum si poate nu am explicat-o nici suficient de complet in anumite locuri din care sa rezulte exact ce vreau sa spun.
In seara asta nu mai am timp, dar o s-o corectez imediat ce gasesc un pic de timp liber.
Posteaza orice nelamurire ai si discutam despre ele cand revin.

Dar asa, in mare, cum ti se pare Geza ?

Scris de **fanel** Sam 09 Mar 2019, 18:14

Demonstrarea pe cale elementara a ipotezei Beal, in cazul exponentilor (2k,2m,2n) se poate face utizand o ecuatie suplimentara, rezolvabila in numere intregi. Demonstratia completa aici https://drive.google.com/file/d/1wrP-xRyeMHudoTDwkFtIiYJR-OjChTwR/view

Scris de **curiosul** Sam 09 Mar 2019, 19:23

Și aici, este apreciabil efortul pe care l-ai depus, dar, din păcate, lucrurile nu se rezumă doar la exponenții pari ai ecuației.

Scris de **curiosul** Sam 09 Mar 2019, 20:30

Analizând mai atent modul de analiză, cu scuzele corespunzătoare pentru situația în care mă înșel, tiparul de analiză este similar celui al utilizatorului nostru "DACU".

Apare aceeași tipologie de interpretare și introducere a unor noi necunoscute în ecuații, pe care le asociez instinctiv cu tiparul utilizatorului Dacu de interpretare și analiză algebrică.

Chiar dacă mă înșel, deși m-aș încuraja eu însumi să cred că vorbim de același utilizator Fanel-Dacu, faptul că vorbim despre un subiect matematic asociat preocupărilor lui Dacu înclin să cred că nu mă înșel și chiar și-așa, nu umbrește cu nimic recunoașterea efortului pe care l-a depus.

Scris de **fanel** Dum 10 Mar 2019, 08:41

Salutari,Curiosule!
De acord ca rezolvarea Ipotezei Beal nu se rezuma numai la cazul demonstrat de mine pentru cazul (2k,2m,2n) pentru exponentii variabilelor , asa cum se poate vedea in link atasat, totusi eu zic ca nefiind vorba de niste cazuri strict particulare, inceputul este destul de bun si faptul ca s-a reusit demonstrarea Ipotezei Beal pentru acest caz "general" este destul de bine.
Fac o rectificare: In demonstrarea Ipotezei Beal prezentata in link , trebuie eliminata conditionarea de coprimalitate a solutiei in presupunerea facuta in cadrul rezolvarii. Scuze tuturor pentru acest lucru!
Nu cunosc pe nimeni de pe forum, deci nici pe Dacu , dar nu ma deranjeaza ca si dansul are abordari similare

Scris de **curiosul** Joi 14 Mar 2019, 20:18

fanel a scris:Salutari,Curiosule!
De acord ca rezolvarea Ipotezei Beal nu se rezuma numai la cazul demonstrat de mine pentru cazul ...
Nu cunosc pe nimeni de pe forum, deci nici pe Dacu , dar nu ma deranjeaza ca si dansul are abordari similare

Ceea ce am subliniat, fiind un tipar asemanator in modul de exprimare, imi confirma faptul ca nu ma insel, dar...tu stii mai bine.
Aspectele matematice le discutam in week-end.

Scris de Continut sponsorizat

Conjectura Beal

Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal

Re: Conjectura Beal