Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Meteorr Astazi la 21:34
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la virgil în NEWTON
( 1 )
» Mesaj de la Meteorr în Global warming is happening?
( 1 )
» Mesaj de la eugen în În ce tip de dovezi aveţi încredere deplină?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| Dacu2 | ||||
| eugen | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Abel Cavaşi |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| virgil | ||||
| Dacu2 | ||||
| Meteorr | ||||
| ilasus | ||||
| CAdi | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 31 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 31 Vizitatori Nici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Deducerea Transformărilor Lorentz-Einstein
+3
Abel Cavaşi
virgil_48
ilasus
7 participanți
Pagina 1 din 3
Pagina 1 din 3 • 1, 2, 3 
 Deducerea Transformărilor Lorentz-Einstein
Deducerea Transformărilor Lorentz-Einstein
Șters
Ultima editare efectuata de catre ilasus in Dum 06 Iun 2021, 18:36, editata de 1 ori
ilasus- Dinamic

- Mulţumit de forum : Numarul mesajelor : 153




Puncte : 11228
Data de inscriere : 14/03/2015
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Asta era de dedus ?ilasus a scris:Presupun că pe o șosea rectilinie pe care sunt fixate două repere O, O’ la distanța x1 unul față de altul, un mobil M se deplasează - în sensul de la O înspre O’ - cu viteza constantă u (u>0), astfel că în momentul inițial (t=0), mobilul M se află în locul inițial, adică în dreptul reperului fix O, iar în momentul t, așadar după un timp t măsurat începând din momentul inițial, mobilul M se află la distanța
x = ut
în raport cu reperul O, respectiv la distanța
x2 = x - x1
în raport cu reperul O’. Deci în raport cu reperele O, O’, mobilul M parcurge distanțele x (în raport cu O), x1 (între O și O’) și x2 (în raport cu O’) în intervalele de timp
t = x/u
t1 = x1/u
și respectiv
t2 = t – t1
Dacă presupun însă că reperul O’ nu este fix, ci unul mobil care se deplasează în același sens cu M și a parcurs x1 = vt
în timpul t cu viteza v
virgil_48- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 11380




Puncte : 44921
Data de inscriere : 03/12/2013
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Trunchiază subiectul. Editarea nu merge. Ce se întâmplă?
ilasus- Dinamic

- Mulţumit de forum : Numarul mesajelor : 153




Puncte : 11228
Data de inscriere : 14/03/2015
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Ce-i cu mesajul ăsta: ’Utilizarea HTML este limitată’?
De ce îmi trunchiază subiectul?
De ce îmi trunchiază subiectul?
ilasus- Dinamic

- Mulţumit de forum : Numarul mesajelor : 153




Puncte : 11228
Data de inscriere : 14/03/2015
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Încerc încă o dată să trimit articolul, poate de data asta reușesc.
ilasus- Dinamic

- Mulţumit de forum : Numarul mesajelor : 153




Puncte : 11228
Data de inscriere : 14/03/2015
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Deducerea Transformărilor Lorentz-Einstein
Deducerea Transformărilor Lorentz-Einstein
Presupun că pe o șosea rectilinie pe care sunt fixate două repere O, O’ la distanța x1 unul față de altul, un mobil M se deplasează - în sensul de la O înspre O’ - cu viteza constantă u (u>0), astfel că în momentul inițial (t=0), mobilul M se află în locul inițial, adică în dreptul reperului fix O, iar în momentul t, așadar după un timp t măsurat începând din momentul inițial, mobilul M se află la distanța
x = ut
în raport cu reperul O, respectiv la distanța
x2 = x - x1
în raport cu reperul O’. Deci în raport cu reperele O, O’, mobilul M parcurge distanțele x (în raport cu O), x1 (între O și O’) și x2 (în raport cu O’) în intervalele de timp
t = x/u
t1 = x1/u
și respectiv
t2 = t – t1
Dacă presupun însă că reperul O’ nu este fix, ci unul mobil care se deplasează în același sens cu M și a parcurs distanța
x1 = vt
în timpul t cu viteza v<u în raport cu O, atunci în raport cu reperul O’, mobilul M parcurge distanța
x2 = x - vt
în timpul
t2 = t – t1 = t – x1/u = t – vt/u = t – (v/u2)x
unde
t1 = (v/u2)x
este timpul în care mobilul M parcurge distanța x1=vt dintre reperele O și O’. În concluzie, dacă în raport cu reperul O, mobilul M se deplasează pe distanța x în timpul t conform relațiilor
(1) x = ut, t = (1/u)x
iar între reperele O și O’, mobilul M se deplasează pe distanța x1 în timpul t1 date de relațiile
(2) x1 = vt, t1 = (v/u2)x
atunci în raport cu reperul O’, mobilul M se deplasează pe distanța x2 în timpul t2 exprimate de relațiile
(3) x2 = x – vt, t2 = t – (v/u2)x
În continuare, despre reperul O’ voi presupune că este fixat pe o platformă aflată în mișcare pe șosea cu viteza constantă v. În acest caz, relațiile (1), (2) și (3) exprimă deplasarea mobilului M pe șosea, deci în raport cu platforma și nu pe platformă. Faptul că ’în raport cu platforma’ nu este totuna cu ’pe platformă’, deci că aceste sintagme exprimă lucruri diferite, mi se pare evident: cât timp mobilul M se deplasează ’în raport cu platforma’, așadar pe șosea, este exclusă posibilitatea ca acesta să fie în mișcare ’pe platformă’. Desigur, însă, că mobilul M se poate deplasa și pe platformă, însă pe o altă distanță x’ diferită de x și într-un alt timp t’ diferit de t, deci distanțele și intervalele de timp parcurse de M pe platformă nu vor putea fi aceleași cu cele parcurse de M pe șosea. De exemplu, dacă presupun că în raport cu reperul O’ fixat pe platformă, mobilul M se deplasează (pe platformă) pe distanța x’ în timpul t’ conform relațiilor
(1’) x’ = ut’, t’ = (1/u)x’
iar între reperele O și O’, mobilul M se deplasează pe distanța x’1 în timpul t’1 date de relațiile
(2’) x’1 = vt’, t’1 = (v/u2)x’
atunci în raport cu reperul O aflat pe șosea, mobilul M se deplasează pe distanța x’2 în timpul t’2 exprimate de relațiile
(3’) x’2 = x’ + vt’, t’2 = t’ + (v/u2)x’
Precizez că relațiile (1’), (2’) și (3’) pot fi deduse în același mod în care au fost deduse și relațiile (1), (2) și (3) din cazul precedent. Însă spre deosebire de primul caz, în care mobilul M și reperul O’ se deplasau în același sens în raport cu reperul O considerat în repaus relativ, în cazul de față mobilul M și reperul O se deplasează în sensuri opuse în raport cu reperul O’ considerat în repaus relativ.
Să remarcăm, în continuare, că distanțele și intervalele de timp omoloage exprimate în relațiile (1), (3’) și (1’), (3), adică distanțele x, x’2 și x’, x2, respectiv intervalele de timp t, t’2 și t’, t2, pot fi cel mult proporționale. Mai exact, factorul k din în egalitățile
(4) x = k(x’ + vt’), t = k(t’ + (v/u2)x’)
(4’) x’ = k(x - vt), t’ = k(t - (v/u2)x)
nu poate fi unitar. De exemplu, dacă încercăm să rezolvăm sistemul de ecuații Cramer (4) în necunoscutele x’, t’, sau sistemul de ecuații Cramer (4’) în necunoscutele x, t, constatăm că acestea au soluțiile (4’) și respectiv (4), numai dacă factorului k îi atribuim valoarea exprimată de relația
(5) k = 1/(1 – v2/u2)1/2
Dacă presupun că u=c, unde c este viteza luminii în vid, atunci relațiile (4), (4'), cu k dat de (5), se identifică cu transformările Lorentz-Einstein, în acest caz k fiind factorul Lorentz.
x = ut
în raport cu reperul O, respectiv la distanța
x2 = x - x1
în raport cu reperul O’. Deci în raport cu reperele O, O’, mobilul M parcurge distanțele x (în raport cu O), x1 (între O și O’) și x2 (în raport cu O’) în intervalele de timp
t = x/u
t1 = x1/u
și respectiv
t2 = t – t1
Dacă presupun însă că reperul O’ nu este fix, ci unul mobil care se deplasează în același sens cu M și a parcurs distanța
x1 = vt
în timpul t cu viteza v<u în raport cu O, atunci în raport cu reperul O’, mobilul M parcurge distanța
x2 = x - vt
în timpul
t2 = t – t1 = t – x1/u = t – vt/u = t – (v/u2)x
unde
t1 = (v/u2)x
este timpul în care mobilul M parcurge distanța x1=vt dintre reperele O și O’. În concluzie, dacă în raport cu reperul O, mobilul M se deplasează pe distanța x în timpul t conform relațiilor
(1) x = ut, t = (1/u)x
iar între reperele O și O’, mobilul M se deplasează pe distanța x1 în timpul t1 date de relațiile
(2) x1 = vt, t1 = (v/u2)x
atunci în raport cu reperul O’, mobilul M se deplasează pe distanța x2 în timpul t2 exprimate de relațiile
(3) x2 = x – vt, t2 = t – (v/u2)x
În continuare, despre reperul O’ voi presupune că este fixat pe o platformă aflată în mișcare pe șosea cu viteza constantă v. În acest caz, relațiile (1), (2) și (3) exprimă deplasarea mobilului M pe șosea, deci în raport cu platforma și nu pe platformă. Faptul că ’în raport cu platforma’ nu este totuna cu ’pe platformă’, deci că aceste sintagme exprimă lucruri diferite, mi se pare evident: cât timp mobilul M se deplasează ’în raport cu platforma’, așadar pe șosea, este exclusă posibilitatea ca acesta să fie în mișcare ’pe platformă’. Desigur, însă, că mobilul M se poate deplasa și pe platformă, însă pe o altă distanță x’ diferită de x și într-un alt timp t’ diferit de t, deci distanțele și intervalele de timp parcurse de M pe platformă nu vor putea fi aceleași cu cele parcurse de M pe șosea. De exemplu, dacă presupun că în raport cu reperul O’ fixat pe platformă, mobilul M se deplasează (pe platformă) pe distanța x’ în timpul t’ conform relațiilor
(1’) x’ = ut’, t’ = (1/u)x’
iar între reperele O și O’, mobilul M se deplasează pe distanța x’1 în timpul t’1 date de relațiile
(2’) x’1 = vt’, t’1 = (v/u2)x’
atunci în raport cu reperul O aflat pe șosea, mobilul M se deplasează pe distanța x’2 în timpul t’2 exprimate de relațiile
(3’) x’2 = x’ + vt’, t’2 = t’ + (v/u2)x’
Precizez că relațiile (1’), (2’) și (3’) pot fi deduse în același mod în care au fost deduse și relațiile (1), (2) și (3) din cazul precedent. Însă spre deosebire de primul caz, în care mobilul M și reperul O’ se deplasau în același sens în raport cu reperul O considerat în repaus relativ, în cazul de față mobilul M și reperul O se deplasează în sensuri opuse în raport cu reperul O’ considerat în repaus relativ.
Să remarcăm, în continuare, că distanțele și intervalele de timp omoloage exprimate în relațiile (1), (3’) și (1’), (3), adică distanțele x, x’2 și x’, x2, respectiv intervalele de timp t, t’2 și t’, t2, pot fi cel mult proporționale. Mai exact, factorul k din în egalitățile
(4) x = k(x’ + vt’), t = k(t’ + (v/u2)x’)
(4’) x’ = k(x - vt), t’ = k(t - (v/u2)x)
nu poate fi unitar. De exemplu, dacă încercăm să rezolvăm sistemul de ecuații Cramer (4) în necunoscutele x’, t’, sau sistemul de ecuații Cramer (4’) în necunoscutele x, t, constatăm că acestea au soluțiile (4’) și respectiv (4), numai dacă factorului k îi atribuim valoarea exprimată de relația
(5) k = 1/(1 – v2/u2)1/2
Dacă presupun că u=c, unde c este viteza luminii în vid, atunci relațiile (4), (4'), cu k dat de (5), se identifică cu transformările Lorentz-Einstein, în acest caz k fiind factorul Lorentz.
Ultima editare efectuata de catre ilasus in Dum 06 Iun 2021, 18:54, editata de 2 ori
ilasus- Dinamic

- Mulţumit de forum : Numarul mesajelor : 153




Puncte : 11228
Data de inscriere : 14/03/2015
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Și există vreo întrebare în topic? Sau se dorește a fi un topic educațional?
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Rog citiți articolul intitulat 'Deducerea Transformărilor Lorentz-Einstein' din postarea precedentă și spuneți-vă punctul de vedere - dacă aveți. Cum se constată, deduc aceste vestite formule doar cu mijloacele fizicii clasice, deci fără a apela la principiile Teoriei Relativității. E posibil? Greșesc pe undeva?
ilasus- Dinamic

- Mulţumit de forum : Numarul mesajelor : 153




Puncte : 11228
Data de inscriere : 14/03/2015
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Păi, totul este ok până la „factorul Lorentz”. Acest factor nu poate fi obținut CONCRET decât în ipoteza că viteza luminii are aceeași valoare față de oricare dintre observatori.
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Din mesajul mai sus citat înțeleg faptul că articolul meu este 'ok', adică este corect. În ce privește valoarea factorului k, aceasta poate fi calculată pentru orice viteze u și respectiv v (v<u), deci și în cazul u=c (c=399 792 458 m/s în vid). Iar dacă (vezi articolul) un mobil M se poate deplasa cu aceeași viteză (u) atât pe șosea, cât și pe platformă, fără a fi necesară o ipoteză în acest scop, în mod sigur o astfel de ipoteză nu va fi necesară nici în cazul în care M este un semnal luminos.Abel Cavaşi a scris:Păi, totul este ok până la „factorul Lorentz”. Acest factor nu poate fi obținut CONCRET decât în ipoteza că viteza luminii are aceeași valoare față de oricare dintre observatori.
ilasus- Dinamic

- Mulţumit de forum : Numarul mesajelor : 153




Puncte : 11228
Data de inscriere : 14/03/2015
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Nu functioneaza bine tiparirea raspunsurilor.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12459
Puncte : 56976
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12459
Puncte : 56976
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Remarcăm că prima egalitate din (3) este de fapt transformarea Galilei, conform căreia mobilul M se deplasează cu viteza u-v în timpul t în raport cu reperul O’ fixat pe platformă. Deci care este adevărul: în raport cu reperul O’ fixat pe platformă, mobilul M se deplasează cu viteza u cum rezultă din relațiile (3), sau cu viteza u-v cum rezultă din transformarea Galilei? Eu cred că transformarea Galilei ignoră intervalele de timp t1 și t2 în care mobilul M se deplasează pe distanțele x1 și respectiv x2, deoarece nu au fost sesizate – dacă Galilei ar fi sesizat aceste intervale de timp, atunci transformarea Galilei s-ar fi identificat cu ambele relații din (3), nu doar cu prima dintre aceste relații. Într-o asemnea ipoteză, care ar fi fost consecințele?ilasus a scris:Presupun că pe o șosea rectilinie pe care sunt fixate două repere O, O’ la distanța x1 unul față de altul, un mobil M se deplasează - în sensul de la O înspre O’ - cu viteza constantă u (u>0), astfel că în momentul inițial (t=0), mobilul M se află în locul inițial, adică în dreptul reperului fix O, iar în momentul t, așadar după un timp t măsurat începând din momentul inițial, mobilul M se află la distanța
x = ut
în raport cu reperul O, respectiv la distanța
x2 = x - x1
în raport cu reperul O’. Deci în raport cu reperele O, O’, mobilul M parcurge distanțele x (în raport cu O), x1 (între O și O’) și x2 (în raport cu O’) în intervalele de timp
t = x/u
t1 = x1/u
și respectiv
t2 = t – t1
Dacă presupun însă că reperul O’ nu este fix, ci unul mobil care se deplasează în același sens cu M și a parcurs distanța
x1 = vt
în timpul t cu viteza v<u în raport cu O, atunci în raport cu reperul O’, mobilul M parcurge distanța
x2 = x - vt
în timpul
t2 = t – t1 = t – x1/u = t – vt/u = t – (v/u2)x
unde
t1 = (v/u2)x
este timpul în care mobilul M parcurge distanța x1=vt dintre reperele O și O’. În concluzie, dacă în raport cu reperul O, mobilul M se deplasează pe distanța x în timpul t conform relațiilor
(1) x = ut, t = (1/u)x
iar între reperele O și O’, mobilul M se deplasează pe distanța x1 în timpul t1 date de relațiile
(2) x1 = vt, t1 = (v/u2)x
atunci în raport cu reperul O’, mobilul M se deplasează pe distanța x2 în timpul t2 exprimate de relațiile
(3) x2 = x – vt, t2 = t – (v/u2)x
ilasus- Dinamic

- Mulţumit de forum : Numarul mesajelor : 153




Puncte : 11228
Data de inscriere : 14/03/2015
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Salut, ilasus!
Cred că ai amestecat situațiile.
Ai formulat mai întâi t1=x1/u pentru situația în care O' este fix, după care x1=vt pentru situația în care O' este în mișcare.
Ce ai făcut tu ulterior, în t2=t-t1, l-ai înlocuit pe t1 din situația cu O' fix în situația cu O' mobil și de aia ai și ajuns la rezultatul la care ai ajuns.
Cred că ai amestecat un pic situațiile și ai dezvoltat ecuațiile ca și cum cele două situații ar fi avut loc simultan, O' fix, O' mobil simultan.
Greșesc?
Cred că ai amestecat situațiile.
Ai formulat mai întâi t1=x1/u pentru situația în care O' este fix, după care x1=vt pentru situația în care O' este în mișcare.
Ce ai făcut tu ulterior, în t2=t-t1, l-ai înlocuit pe t1 din situația cu O' fix în situația cu O' mobil și de aia ai și ajuns la rezultatul la care ai ajuns.
Cred că ai amestecat un pic situațiile și ai dezvoltat ecuațiile ca și cum cele două situații ar fi avut loc simultan, O' fix, O' mobil simultan.
Greșesc?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
În mesajul în care ai și dezvoltat până la factorul Lorentz restul mi se pare ok, doar asta cred eu că e greșeala.
În schimb, ciudățenia faptului că ai ajuns "galileean" la factorul Lorentz , din expunerea ta se poate "extrage" tocmai principiul relativității restrânse.
Interpretând altfel expunerea ta, dacă ai considera un reper, O' în cazul tău, simultan atât în mișcare, cât și în repaus, poți să ajungi la factorul Lorentz.
În schimb, în TRS, postulând că lumina are aceeași viteză indiferent de sistemul de referință, fie că se mișcă, fie că e în repaus, ai putea inversa asocierea exact cu ceea ce ai greșit tu, adică ai putea considera acel sistem de referință atât în repaus, cât și în mișcare simultan (raportat la constanta vitezei luminii).
În schimb, ciudățenia faptului că ai ajuns "galileean" la factorul Lorentz , din expunerea ta se poate "extrage" tocmai principiul relativității restrânse.
Interpretând altfel expunerea ta, dacă ai considera un reper, O' în cazul tău, simultan atât în mișcare, cât și în repaus, poți să ajungi la factorul Lorentz.
În schimb, în TRS, postulând că lumina are aceeași viteză indiferent de sistemul de referință, fie că se mișcă, fie că e în repaus, ai putea inversa asocierea exact cu ceea ce ai greșit tu, adică ai putea considera acel sistem de referință atât în repaus, cât și în mișcare simultan (raportat la constanta vitezei luminii).
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Greșești. Raționamentul e alcătuit din doua părți pentru claritatea expunerii. De fapt prima parte – cea în care O’ se află la distanța fixă x1 în raport cu O - nici nu e necesar să fie prezentată. Sper să-ți dai seama – în caz contrar, putem discuta mai pe larg despre acest aspect. În ce privește restul comentariilor, eu cred că ai să le reformulezi dacă vei vedea o variantă mai nouă a articolului (o pot prezenta și aici dar înțeleg că nu merg actualizările) – vezi prima postare a lui ilasus (adică a mea) din topicul ’relații ilasusiene’ pe scientia.ro: https://forum.scientia.ro/index.php/topic,5491.0.html
ilasus- Dinamic

- Mulţumit de forum : Numarul mesajelor : 153




Puncte : 11228
Data de inscriere : 14/03/2015
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Măi ilasus, am recitit, am reanalizat și parcă tot mi se pare că ai încurcat "borcanele".
Sau mai bine zis le-ai amestecat.
S-o luăm pas cu pas.
Dacă x1=vt înseamnă că în momentul t=0, O coincide cu O', pentru că altfel, dacă în momentul t0 între O și O' este o distanță x'1, atunci ecuația completă ar fi x1=x'1 +vt.
Dacă nu l-ai luat în calcul pe x'1, înțeleg că O coincide cu O' la momentul t=0, iar cât timp t, corpul M parcurge distanța x, reperul O' parcurge distanța x1, ambele față de O.
Atunci, în situația cu O' mobil, t1 nu mai este același din situația cu O' fix la distanță x1 de O, t1 reprezentând timpul necesar lui M pentru a parcurge distanța dintre O și O'.
În acest caz, cu O' mobil, ai un alt timp t'1 necesar lui M pentru a parcurge distanța dintre O și O', care nu mai este x1, pentru că x1 este distanța dintre O și O' la momentul t.
În consecință, nu mi se pare corect să înlocuiești ulterior, în t2=t-t1, pe t1 cu x1/u.
Dacă procedezi așa înseamnă că t=t1.
Din acest motiv am zis că ai amestecat situațiile.
Corectează-mă dacă greșesc.
Sau mai bine zis le-ai amestecat.
S-o luăm pas cu pas.
Dacă x1=vt înseamnă că în momentul t=0, O coincide cu O', pentru că altfel, dacă în momentul t0 între O și O' este o distanță x'1, atunci ecuația completă ar fi x1=x'1 +vt.
Dacă nu l-ai luat în calcul pe x'1, înțeleg că O coincide cu O' la momentul t=0, iar cât timp t, corpul M parcurge distanța x, reperul O' parcurge distanța x1, ambele față de O.
Atunci, în situația cu O' mobil, t1 nu mai este același din situația cu O' fix la distanță x1 de O, t1 reprezentând timpul necesar lui M pentru a parcurge distanța dintre O și O'.
În acest caz, cu O' mobil, ai un alt timp t'1 necesar lui M pentru a parcurge distanța dintre O și O', care nu mai este x1, pentru că x1 este distanța dintre O și O' la momentul t.
În consecință, nu mi se pare corect să înlocuiești ulterior, în t2=t-t1, pe t1 cu x1/u.
Dacă procedezi așa înseamnă că t=t1.
Din acest motiv am zis că ai amestecat situațiile.
Corectează-mă dacă greșesc.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Ca să judeci corect, trebuie să ai în vedere că te afli în momentul t și analizezi două cazuri echivalente în legătură cu distanța x1 parcursă de M cu viteza u în timpul t1: 1) O’ a rămas în repaus în timpul t la distanța x1 în raport cu O (x1=ut1) și 2) O’ s-a deplasat cu viteza v în timpul t pe distanța x1 în raport cu O (x1=vt). Deci în aceste cazuri vorbim de aceeași distanță x1=ut1=vt și de același timp t1=x1/u=vt/u. Mai poți remarca, dacă vrei, că pe de-o parte, M și O’ au parcurs aceeași distanță x1 cu viteze diferite (u și respectiv v) în intervale de timp diferite (t1 și respectiv t), și pe de altă parte, că în același timp t, M și O’ au parcurs distanțe diferite (x și respectiv x1) cu viteze diferite (u și respectiv v).
ilasus- Dinamic

- Mulţumit de forum : Numarul mesajelor : 153




Puncte : 11228
Data de inscriere : 14/03/2015
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Mai întâi, hai să lămurim un lucru.
t1 reprezintă timpul necesar lui M pentru a parcurge distanța echivalentă dintre O și O', corect?
Plecând de la asta, ne referim strict la distanța dintre O și O'.
În cazul 2, cu O' mobil, ceea ce ne interesează este momentul când distanța dintre O și O' este egală cu distanța parcursă de M.
Că notațiile t1 și x1 pe care le-ai folosit asta exprimă ele și despre asta vorbesc ele.
Și aici e problema, fie a mea, fie a ta, rămâne să lămurim.
Nu știu dacă înțelegi ce vreau să spun, dar discutăm.
Eventual și pe baza animației din mesajul anterior.
t1 reprezintă timpul necesar lui M pentru a parcurge distanța echivalentă dintre O și O', corect?
Plecând de la asta, ne referim strict la distanța dintre O și O'.
În cazul 2, cu O' mobil, ceea ce ne interesează este momentul când distanța dintre O și O' este egală cu distanța parcursă de M.
Că notațiile t1 și x1 pe care le-ai folosit asta exprimă ele și despre asta vorbesc ele.
Și aici e problema, fie a mea, fie a ta, rămâne să lămurim.
Nu știu dacă înțelegi ce vreau să spun, dar discutăm.
Eventual și pe baza animației din mesajul anterior.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Cred totuși că e o problemă de context undeva și asta ne duce în eroare, fie pe mine, fie pe tine.
Ia să vedem!
Din modul în care ai folosit notațiile eu înțeleg așa:
t1 este timpul necesar lui M pentru a parcurge o distanță x1 , echivalentă cu distanța dintre O și O'
Iar problema de context apare în momentul în care O' este mobil la rândul lui pentru că între O și O' este o distanță care se modifică continuu, dar diferă momentul de timp în care distanța parcursă de M este echivalentă cu cea dintre O și O'.
Într-un singur moment de timp, t1, vorbim de această distanță parcursă de M echivalentă cu cea dintre O și O', când O' este mobil, moment t1 care corespunde atât în cronometrarea mișcării lui O', cât și a lui M, analizând mișcarea lor plecând de la același t=0.
Nu știu ce se înțelege din ce-am scris, în sfârșit...
Moment de timp t1 care nu mai corespunde cu cel din situația în care O' AR FI fix, nu ESTE fix.
Aici este nedumerirea mea și dacă am dreptate, atunci aici este eroarea ta de raționament care te-a și condus la rezultatul și concluziile finale.
Pentru că ai "amestecat" situațiile.
Cred eu.
Ia să vedem!
Din modul în care ai folosit notațiile eu înțeleg așa:
t1 este timpul necesar lui M pentru a parcurge o distanță x1 , echivalentă cu distanța dintre O și O'
Iar problema de context apare în momentul în care O' este mobil la rândul lui pentru că între O și O' este o distanță care se modifică continuu, dar diferă momentul de timp în care distanța parcursă de M este echivalentă cu cea dintre O și O'.
Într-un singur moment de timp, t1, vorbim de această distanță parcursă de M echivalentă cu cea dintre O și O', când O' este mobil, moment t1 care corespunde atât în cronometrarea mișcării lui O', cât și a lui M, analizând mișcarea lor plecând de la același t=0.
Nu știu ce se înțelege din ce-am scris, în sfârșit...
Moment de timp t1 care nu mai corespunde cu cel din situația în care O' AR FI fix, nu ESTE fix.
Aici este nedumerirea mea și dacă am dreptate, atunci aici este eroarea ta de raționament care te-a și condus la rezultatul și concluziile finale.
Pentru că ai "amestecat" situațiile.
Cred eu.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
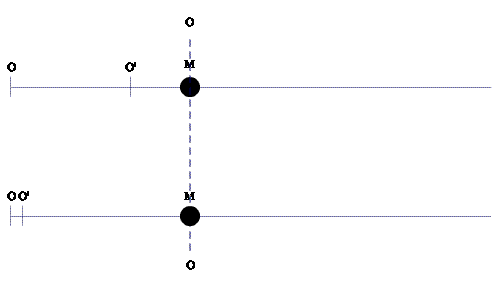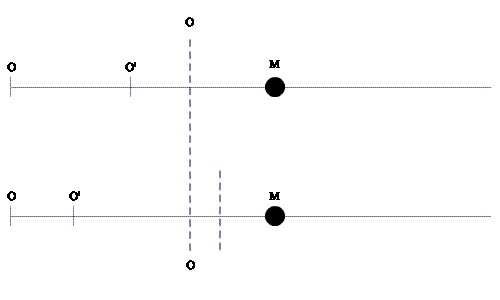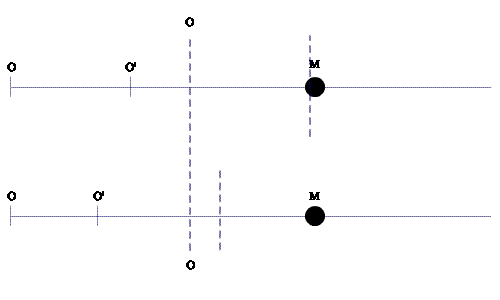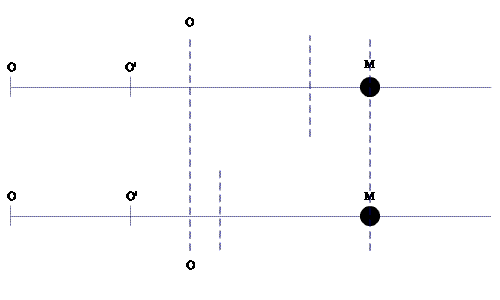
Încerc să stabilesc la ce te gândești tu ca să ma gândesc și eu la același lucru. Cred că te gândești la M care parcurge distanța dintre O și O’ în cele două cazuri notate de mine cu 1), când M parcurge distanța fixă x1 dintre O și O’ și 2), când M parcurge distanța variabilă x1 dintre O și O’ – parcursă de O’ în timpul t cu viteza v. Și probabil dorești să sugerezi prin intermediul animației că x1 și t1 în cele două cazuri ar fi diferite. Dacă e așa, atunci nu văd ce te face să crezi că x1 și t1 din aceste cazuri sunt într-adevăr diferite?
Pentru simplitate, am să consder un exemplu. Presupun că în timpul t=5s, M și O’ se deplasează cu vitezele u=5m/s și respectiv v=3m/s în raport cu O. Atunci x=25m, x1=15m și x2=10m, iar t1=(v/u2)x=3s și t2=2s. Deci în cazul 1), M a parcurs distanța fixă x1=15m în timpul t1=3s cu viteza u=5m/s, iar în cazul 2), caz în care O’ a parcurs distanța x1=15m în timpul t=5s cu viteza v=3m/s, M a parcurs distanța variabilă x1=15m în timpul t=3s cu viteza u=5m/s, ca și în cazul 1). Deci unde este diferența dintre cazurile 1) și 2) pe care o sugerează giful animat?
Pentru simplitate, am să consder un exemplu. Presupun că în timpul t=5s, M și O’ se deplasează cu vitezele u=5m/s și respectiv v=3m/s în raport cu O. Atunci x=25m, x1=15m și x2=10m, iar t1=(v/u2)x=3s și t2=2s. Deci în cazul 1), M a parcurs distanța fixă x1=15m în timpul t1=3s cu viteza u=5m/s, iar în cazul 2), caz în care O’ a parcurs distanța x1=15m în timpul t=5s cu viteza v=3m/s, M a parcurs distanța variabilă x1=15m în timpul t=3s cu viteza u=5m/s, ca și în cazul 1). Deci unde este diferența dintre cazurile 1) și 2) pe care o sugerează giful animat?
ilasus- Dinamic

- Mulţumit de forum : Numarul mesajelor : 153




Puncte : 11228
Data de inscriere : 14/03/2015
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Facem altfel.
Hai să luăm în calcul doar cazul 2 când O' este în mișcare și să stabilim semnificația notațiilor.
x1 este distanța parcursă de M echivalentă cu cea dintre O și O' la momentul t1 sau la momentul t?
Dacă e la momentul t, ce reprezintă t1 ?
Dacă e la momentul t1 , cu t1 mai mic decât t, atunci la momentul t ce distanță este între O și O'?
Repet, fă complet abstracție de cazul 1.
Hai să luăm în calcul doar cazul 2 când O' este în mișcare și să stabilim semnificația notațiilor.
x1 este distanța parcursă de M echivalentă cu cea dintre O și O' la momentul t1 sau la momentul t?
Dacă e la momentul t, ce reprezintă t1 ?
Dacă e la momentul t1 , cu t1 mai mic decât t, atunci la momentul t ce distanță este între O și O'?
Repet, fă complet abstracție de cazul 1.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Citește doar cazul care te interesează.
Cazul 1). O’ se află la distanța x1=15m față de O în tot timpul t=5s cât durează experimentul, adică din momentul inițial t=0s când e pornit cronometrul, moment în care M se află în același loc cu O, și până in momentul t=5s in care M ajunge la distanța x=ut=25m în raport cu O. Deci în acest caz, M a parcurs distanța x=ut=25m în timpul t=5s cât a durat experimentul, distanța x1=ut1=15m între O și O’ în timpul t1=3s, și distanța x2=ut2=10m în raport cu O’ în timpul t2=2s.
Cazul 2). M și O’ pornesc simultan din O în momentul t=0s de pe cronometru. După un timp t=3s, M ajunge la distanța x1=ut1=15m, iar O’ ajunge la distanța vt1=9m în raport cu O. După încă două secunde, așadar după un timp t=5s de la start, M ajunge la distanța x=ut=25m, iar O’ ajunge la distanța x1=vt=15m. Deci în acest caz, M a parcurs distanța x=ut=25m în timpul t=5s cât a durat experimentul, distanța x1=ut1=15m între O și O’ în timpul t1=3s (în momentul t=5s, distanța x1=ut1=15m parcursă de M în timpul t1=3s cu viteza u=5m/s este aceeași cu distanța x1=vt=15m parcursă de O’ în raport cu O în timpul t=5s cu viteza v=3m/s), și respectiv distanța x2=ut2=10m în raport cu O’ în timpul t2=2s.
Cazul 1). O’ se află la distanța x1=15m față de O în tot timpul t=5s cât durează experimentul, adică din momentul inițial t=0s când e pornit cronometrul, moment în care M se află în același loc cu O, și până in momentul t=5s in care M ajunge la distanța x=ut=25m în raport cu O. Deci în acest caz, M a parcurs distanța x=ut=25m în timpul t=5s cât a durat experimentul, distanța x1=ut1=15m între O și O’ în timpul t1=3s, și distanța x2=ut2=10m în raport cu O’ în timpul t2=2s.
Cazul 2). M și O’ pornesc simultan din O în momentul t=0s de pe cronometru. După un timp t=3s, M ajunge la distanța x1=ut1=15m, iar O’ ajunge la distanța vt1=9m în raport cu O. După încă două secunde, așadar după un timp t=5s de la start, M ajunge la distanța x=ut=25m, iar O’ ajunge la distanța x1=vt=15m. Deci în acest caz, M a parcurs distanța x=ut=25m în timpul t=5s cât a durat experimentul, distanța x1=ut1=15m între O și O’ în timpul t1=3s (în momentul t=5s, distanța x1=ut1=15m parcursă de M în timpul t1=3s cu viteza u=5m/s este aceeași cu distanța x1=vt=15m parcursă de O’ în raport cu O în timpul t=5s cu viteza v=3m/s), și respectiv distanța x2=ut2=10m în raport cu O’ în timpul t2=2s.
ilasus- Dinamic

- Mulţumit de forum : Numarul mesajelor : 153




Puncte : 11228
Data de inscriere : 14/03/2015
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Ok, am înțeles și unde îmi dădea mie cu virgulă.
Complicam eu lucrurile inutil ducându-mă în eroare acel "între O și O' ".
Complicam eu lucrurile inutil ducându-mă în eroare acel "între O și O' ".
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Dacă nu mai există și alte nedumeriri și consideri totul OK, atunci să revenim la întrebarea pusă. Deci tu ce părere ai, mobilul M se deplasează cu viteza u=5m/s în raport cu platforma, așa cum rezultă din relațiile (3) (și cum am precizat și în postarea precedentă), sau cu viteza u-v=3m/s, așa cum rezultă din transformearea Galilei exprimată în prima egalitate din (3) - și cum știe, de altfel, toată lumea?
ilasus- Dinamic

- Mulţumit de forum : Numarul mesajelor : 153




Puncte : 11228
Data de inscriere : 14/03/2015
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Exemplul tău numeric a fost destul de clarificator, iar ceea ce vrei tu să subliniezi prin întrebarea ta este faptul că prin metoda aceasta a ta de "segmentare în doi timpi" a mișcării, viteza lui M față de O' rezultă ca fiind aceeași, fie că O' este în repaus față de O, fie că O' este în mișcare față de O.
Ia să vedem.
În cazul 2, cu O' în mișcare față de O, prin metoda ta ai obținut distanța x2 parcursă de M față de O' și (sau în) timpul t2 .
Carevasăzică, în acest fel și în această situație cu O' mobil față de O, viteza lui M față de O' este x2 / t2 .
Înlocuind valorile respective, și anume,
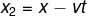
și
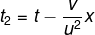
înlocuindu-l pe t cu x/u ajungi la

Deci prin metoda ta, pentru cazul 2 când și O' este în mișcare față de O cu viteză v, viteza lui M față de O' este tot u, nu este u-v.
Este atât interesant, cât și întrebător, la modul că pe undeva este o greșeală de raționament.
Mai lasă-mă un pic să cântăresc situația.
Cred totuși că undeva ceva este greșit.
Nu în dezvoltarea ecuațiilor, ci mai degrabă în raționamentul pe care l-ai folosit pentru a le construi.
Revin.
Ia să vedem.
În cazul 2, cu O' în mișcare față de O, prin metoda ta ai obținut distanța x2 parcursă de M față de O' și (sau în) timpul t2 .
Carevasăzică, în acest fel și în această situație cu O' mobil față de O, viteza lui M față de O' este x2 / t2 .
Înlocuind valorile respective, și anume,
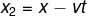
și
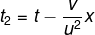
înlocuindu-l pe t cu x/u ajungi la

Deci prin metoda ta, pentru cazul 2 când și O' este în mișcare față de O cu viteză v, viteza lui M față de O' este tot u, nu este u-v.
Este atât interesant, cât și întrebător, la modul că pe undeva este o greșeală de raționament.
Mai lasă-mă un pic să cântăresc situația.
Cred totuși că undeva ceva este greșit.
Nu în dezvoltarea ecuațiilor, ci mai degrabă în raționamentul pe care l-ai folosit pentru a le construi.
Revin.
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Analizăm doar cazul 2 pentru că în această situație ceva dă cu virgulă și s-o luăm din aproape în aproape în sens invers, analizând distanța x2 și timpul t2, să vedem ce și unde nu se potrivește.
În mod evident, distanța parcursă de M față de O' în mișcare cu viteză v este x2=x-vt.
Deci problema e undeva la numitor și ce îmi sare în ochi este pătratul lui "u" din expresia lui t2.

Să vedem cum a apărut acel u pătrat și analizând ecuațiile și raționamentul în sens invers, se ajunge, de fapt, la expresia lui t1 care conține acest pătrat.
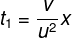
Deci problema e undeva la t1.
Aici s-a ajuns de la:

În continuare, reprezintă timpul în care M parcurge distanța x1 dintre O și O'.
reprezintă timpul în care M parcurge distanța x1 dintre O și O'.
Și aici apare și problema pe care o și tot menționam eu, dar ori nu o înțelegeai tu, ori nu o explicam eu inteligibil și reformulez.
Când ai înlocuit x1 cu vt apare contradicția cu semnificația notației x1 la nivelul mișcării lui M, pe care ai "extras-o", ai "preluat-o" din primul caz, cel în care O' este fix.
Nu atât al lui x1 , cât mai degrabă cu cea a lui t1.
Pentru că în acest fel t1 ar trebui să aibă valoarea lui t în al doilea caz cu O' mobil.
Pentru că dacă t1 semnifică timpul necesar lui M pentru a parcurge distanța echivalentă cu cea dintre O și O', iar tu ai luat pentru asta în calcul distanța "finală" parcursă de O', cea tot de x1, atunci timpul t1 este timpul necesar lui O' pentru a parcurge distanța x1, adică t.
Aici era problema de interpretare și cum îți spuneam, ai amestecat situațiile, ai preluat din cazul 1 aceeași distanță x1 și pentru cazul 2 și bineînțeles, îți va rezulta același timp t1.
Dacă apare același timp t1 și aceeași distanță x1, din t2 = t- t1 și x2 = x-x1, normal că obții aceeași viteză pentru M față de O' mobil ca și în cazul lui O' fix.
Înțelegi ce vreau să spun sau încerc să fiu mai clar?
În mod evident, distanța parcursă de M față de O' în mișcare cu viteză v este x2=x-vt.
Deci problema e undeva la numitor și ce îmi sare în ochi este pătratul lui "u" din expresia lui t2.

Să vedem cum a apărut acel u pătrat și analizând ecuațiile și raționamentul în sens invers, se ajunge, de fapt, la expresia lui t1 care conține acest pătrat.
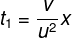
Deci problema e undeva la t1.
Aici s-a ajuns de la:

În continuare,
 reprezintă timpul în care M parcurge distanța x1 dintre O și O'.
reprezintă timpul în care M parcurge distanța x1 dintre O și O'.Și aici apare și problema pe care o și tot menționam eu, dar ori nu o înțelegeai tu, ori nu o explicam eu inteligibil și reformulez.
Când ai înlocuit x1 cu vt apare contradicția cu semnificația notației x1 la nivelul mișcării lui M, pe care ai "extras-o", ai "preluat-o" din primul caz, cel în care O' este fix.
Nu atât al lui x1 , cât mai degrabă cu cea a lui t1.
Pentru că în acest fel t1 ar trebui să aibă valoarea lui t în al doilea caz cu O' mobil.
Pentru că dacă t1 semnifică timpul necesar lui M pentru a parcurge distanța echivalentă cu cea dintre O și O', iar tu ai luat pentru asta în calcul distanța "finală" parcursă de O', cea tot de x1, atunci timpul t1 este timpul necesar lui O' pentru a parcurge distanța x1, adică t.
Aici era problema de interpretare și cum îți spuneam, ai amestecat situațiile, ai preluat din cazul 1 aceeași distanță x1 și pentru cazul 2 și bineînțeles, îți va rezulta același timp t1.
Dacă apare același timp t1 și aceeași distanță x1, din t2 = t- t1 și x2 = x-x1, normal că obții aceeași viteză pentru M față de O' mobil ca și în cazul lui O' fix.
Înțelegi ce vreau să spun sau încerc să fiu mai clar?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
Hai să mă exprim altfel, ilasus, poate un pic mai simplu și mai general.
Greșeala ta din cazul 2, foarte subtilă ce-i drept, s-a strecurat aici:

când ai înlocuit x1 cu vt.
Pentru că în mișcarea lui M , x1 este distanță corespondentă momentului de timp t1, iar în mișcarea lui O' , x1 este distanță corespondentă momentului de timp t, nu tot a momentului de timp t1.
Înțelegi ce vreau să punctez?
Greșeala ta din cazul 2, foarte subtilă ce-i drept, s-a strecurat aici:

când ai înlocuit x1 cu vt.
Pentru că în mișcarea lui M , x1 este distanță corespondentă momentului de timp t1, iar în mișcarea lui O' , x1 este distanță corespondentă momentului de timp t, nu tot a momentului de timp t1.
Înțelegi ce vreau să punctez?
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Deducerea Transformărilor Lorentz-Einstein
Re: Deducerea Transformărilor Lorentz-Einstein
În momentul prezent t, presupunînd că acesta e momentul când se face analiza cazului 2, x1 este o distanță fixă și este singura distanță pe care s-a deplasat atât M, în timpul t1, cât și O’, însă în timpul t. Deci este vorba despre o distanță unică (x1), parcursă de două obiecte diferite (mobilul M și reperul O’), în imtervale de timp diferite (t1 și respectiv t), cu viteze diferite (u și respectiv v). De aici eu am tras concluzia că în momentul t, x1=vt=ut1 (momentul prezent t este ulterior momentului t1, deci t1<t atât ca momente de timp, cât și ca intervale de timp). Deocamdată tu vezi însă două distanțe x1 (cum pot fi două dacă e una singură?), deoarece timpul în care e parcursă și viteza cu care e parcursă o distanță îi atribuie niște proprietăți speciale datorită cărora distanța respectivă se multiplică (!). Poate n-am înțeles eu bine, dar cam așa rezultă din comentariile tale. Poți să explici mai clar ce vrei să spui?
ilasus- Dinamic

- Mulţumit de forum : Numarul mesajelor : 153




Puncte : 11228
Data de inscriere : 14/03/2015
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
Pagina 1 din 3 • 1, 2, 3 
 Subiecte similare
Subiecte similare» Transformările Galilei și Lorentz.
» O altă perspectivă asupra transformărilor relativiste – posibile implicaţii
» Einstein si eterul
» O altă perspectivă asupra transformărilor relativiste – posibile implicaţii
» Einstein si eterul
Pagina 1 din 3
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit