O exceptionala problema inca nerezolvata

virgil_48 a scris:Daca ai fi citit cu atentie ce este scris in acest topic, ti-ai fi dat
seama ca am sustinut, cu anumite deosebiri de abordare,
acelasi lucru. Nu m-ai contrazis. Poti fi linistit.

virgil_48 a scris:Vrei sa deschizi un topic despre nivelul meu de pregatire ?  

Dacu a scris:

virgil a scris:

virgil a scris:
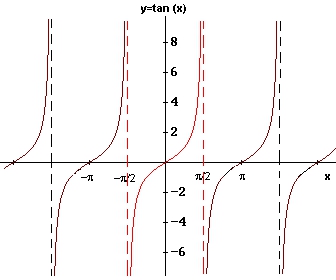
Eu nu am raspuns pentru ca am considerat subiectul incheiat. Faptul ca raza de curbura poate lua valori intre 0 si +infinit este simplu de imaginat daca te gandesti cum variaza graficul functiei tangenta. Daca trigonometric se poate, inseamna ca exista un raspuns la intrebarea ta, mai mult decat atat acest grafic sugereaza ca nu exista traiectorii rectilinii decat traiectorii care pot fi considerate rectilinii, deoarece trecerea de la zero la infinit trece prin valori diferite. Deci linia dreapta este un caz particular al liniei curbe.

1) Ești de-acord cu raționamentul meu și anume "Pentru cei care se află în repaus peTerra și privesc traiectoria pietrei pe toată perioada experimentului și dacă piatra este sferică și nu sunt curenți de aer perturbatori atunci traiectoria pietrei face parte din verticala locului din care a fost aruncată ceea ce înseamnă că piatra se deplasează tot timpul pe o traiectorie având curbura egală cu zero."?
2) Care este curbura traiectoriei pietrei pentru cei care se află în mișcare pe Terra cu viteza și privesc traiectoria pietrei pe toată perioada experimentului iar piatra este sferică și nu sunt curenți de aer perturbatori?

virgil a scris:

Dacu a scris:

virgil a scris:

1) Ești de-acord cu raționamentul meu și anume "Pentru cei care se află în repaus peTerra și privesc traiectoria pietrei pe toată perioada experimentului și dacă piatra este sferică și nu sunt curenți de aer perturbatori atunci traiectoria pietrei face parte din verticala locului din care a fost aruncată ceea ce înseamnă că piatra se deplasează tot timpul pe o traiectorie având curbura egală cu zero."?
2) Care este curbura traiectoriei pietrei pentru cei care se află în mișcare pe Terra cu viteza și privesc traiectoria pietrei pe toată perioada experimentului iar piatra este sferică și nu sunt curenți de aer perturbatori?

1). Pe distante scurte asa este, curbura pare a fi zero. Dar daca piatra este aruncata la inaltime mare, verticala locului nu mai corespunde datorita rotatiei Pamantului  care actioneaza asupra pietrei in cadere libera, asa ca locul de cadere nu mai corespunde cu locul de aruncare. Pentru ca locul de cadere sa corespunda cu locul de aruncare, ar trebui ca Pamantul sa nu se roteasca, sau piatra sa primeasca o corectie pe timpul zborului in sensul de rotatie a Pamantului, pentruca la momentul aruncarii piatra are si o viteza tangentiala egala cu viteza periferica  de rotatie a Pamantului, dar pe masura ce se indeparteaza de pamant creste raza de rotatie a pietrei in jurul axei pamantului, dar viteza tangentiala ramane constanta, deci piatra va ramane in urma sensului de rotatie a Pamantului, si va cadea la o oarecare distanta fata de punctul de aruncare.
2). Depinde fata de ce repere privesti miscarea pietrei. De exemplu daca piatra este aruncata la verticala paralel cu un stalp de telegraf aflat foarte aproape, ai sa observi ca piatra se deplaseaza paralel cu stalpul (evident pe inaltimea relativ mica a stalpului, ca sa nu intervina in mod evident influienta rotatiei Pamantului). Daca nu ai nici un reper, nici macar punctul de aruncare, ai sa vezi ca piatra are o traiectorie parabolica. Dar este doar o traiectorie aparenta, asemanator cu deformarea aparenta a traiectoriilor planetelor vazute de pe Pamant ca fiind niste curbe intortochiate numite ecliptice.

virgil a scris:. . . . .
1). Pe distante scurte asa este, curbura pare a fi zero. Dar daca piatra este aruncata la inaltime mare, verticala locului nu mai corespunde datorita rotatiei Pamantului  care actioneaza asupra pietrei in cadere libera, asa ca locul de cadere nu mai corespunde cu locul de aruncare. Pentru ca locul de cadere sa corespunda cu locul de aruncare, ar trebui ca Pamantul sa nu se roteasca, sau piatra sa primeasca o corectie pe timpul zborului in sensul de rotatie a Pamantului, pentruca la momentul aruncarii piatra are si o viteza tangentiala egala cu viteza periferica  de rotatie a Pamantului, dar pe masura ce se indeparteaza de pamant creste raza de rotatie a pietrei in jurul axei pamantului, dar viteza tangentiala ramane constanta, deci piatra va ramane in urma sensului de rotatie a Pamantului, si va cadea la o oarecare distanta fata de punctul de aruncare.
2). Depinde fata de ce repere privesti miscarea pietrei. De exemplu daca piatra este aruncata la verticala paralel cu un stalp de telegraf aflat foarte aproape, ai sa observi ca piatra se deplaseaza paralel cu stalpul (evident pe inaltimea relativ mica a stalpului, ca sa nu intervina in mod evident influienta rotatiei Pamantului). Daca nu ai nici un reper, nici macar punctul de aruncare, ai sa vezi ca piatra are o traiectorie parabolica. Dar este doar o traiectorie aparenta, asemanator cu deformarea aparenta a traiectoriilor planetelor vazute de pe Pamant ca fiind niste curbe intortochiate numite ecliptice.

Dacu a scris:

1) Eu cred că atunci când a fost aruncată piatra a preluat datorită inerției și efectul rotației Terrei în jurul axei sale.Scade acest efect al rotației Terrei în jurul axei sale pe măsură ce piatra se deplasează?Eu nu văd cum ar putea să scadă acest efect...Fă te rog un calcul al distanței maxime parcursă de piatră astfel încât traiectoria acesteia să aibă pe toată perioada deplasării curbura egală cu zero.
2) Eu cred că odată ce stâlpul vertical este legat solidar de Terra , atunci când eu sunt în mișcare voi vedea traiectoria ca fiind o curbă cu raza de curbură diferită de zero și deci aceasta curbă nu pot să o văd ca fiind paralelă cu stâlpul.Curba aceea pe care o văd se datorează mișcării mele și se datorează faptului că eu privesc mișcarea pietrei đin sistemul meu propriu de referință care nu mai este legat solidar de Terra.Dacă aș sta pe loc adică ceea ce este totuna cu a fi solidar legat de Terra , atunci traiectoria pietrei va fi o curbă cu raza de curbură egala cu zero.

virgil a scris:

Dacu a scris:

1) Eu cred că atunci când a fost aruncată piatra a preluat datorită inerției și efectul rotației Terrei în jurul axei sale.Scade acest efect al rotației Terrei în jurul axei sale pe măsură ce piatra se deplasează?Eu nu văd cum ar putea să scadă acest efect...Fă te rog un calcul al distanței maxime parcursă de piatră astfel încât traiectoria acesteia să aibă pe toată perioada deplasării curbura egală cu zero.
2) Eu cred că odată ce stâlpul vertical este legat solidar de Terra , atunci când eu sunt în mișcare voi vedea traiectoria ca fiind o curbă cu raza de curbură diferită de zero și deci aceasta curbă nu pot să o văd ca fiind paralelă cu stâlpul.Curba aceea pe care o văd se datorează mișcării mele și se datorează faptului că eu privesc mișcarea pietrei đin sistemul meu propriu de referință care nu mai este legat solidar de Terra.Dacă aș sta pe loc adică ceea ce este totuna cu a fi solidar legat de Terra , atunci traiectoria pietrei va fi o curbă cu raza de curbură egala cu zero.

1. Pentru ca piatra aruncata sa fie mereu deasupra punctului de lansare, trebuie sa aiba tot timpul zborului aceiasi viteza unghiulara cu Pamantul. Cum viteza unghiulara omega este egala cu raportul dintre viteza tangentiala (Vt), adica viteza de rotatie a Pamantului in punctul considerat, sau punctul de lansare, si raza (R) a Pamantului plus inaltimea (h) pana la care se ridica piatra. Deci;
- pentru punctul de lansare (aruncare) viteza unghiulara este;  Omega,P= Vt/R ;
- pentru piatra aflata la inaltimea h viteza unghiulara (Omega,h) este;
Omega,h =Vt/(R+h) ;
Comparand cele doua viteze unghiulare, ale punctului de aruncare de pe Pamant cu viteza unghiulara a pietrei aflata la inaltimea h, se vede ca piatra ramane in urma punctului de aruncare deoarece are viteza unghiulara mai mica, cu cat inaltimra h este mai mare. Astfel piatra nu cade niciodata exact in punctul de aruncare pe verticala.

La punctul doi se aplica tot punctul unu, doar ca efectul optic este altul. Daca privesti piatra si stalpul in acelasi timp ai sa vezi ca piatra coboara paralel cu stalpul. Daca privesti doar piatra ti se pare ca coboara pe o curba.

virgil a scris:Soarele rasare de la rasarit, deci pamantul se roteste dinspre vest spre est. Asta inseamna ca piatra aruncata ramane in urma locului de aruncare, adica deviata spre vest. Pentru calculul exact trebuie sa cunosti pozitia pe meridianul locului de aruncare, cu ajutorul caruia trebuie sa calculezi raza cercului paralelei Pamantului, din punctul de aruncare (adica distanta de la punctul de aruncare pana la axa de rotatie a Pamantului, care este mai mica decat raza sferei pamantului.) Cunoscand aceasta distanta se poate afla viteza periferica a Pamantului la locul de aruncare, stiind ca viteza periferica este maxima la ecuator si zero la poli, in timp ce viteza unghiulara este aceiasi. Apoi cunoscand inaltimea h la care aruncam piatra se poate calcula folosind relatiile scrise anterior care este arcul de cerc descris de locul de aruncare, si arcul de cerc descris de punctul de inaltime maxima al pietrei. Desigur timpul de urcare se insumeaza cu timpul de coborare. Vom avea doua viteze periferice si un acelasi timp. Inmultindu-le vom gasi doua lungimi a caror diferenta ne arata cu cat ramane in urma piatra, la cadere fata de locul de lansare. Dar pentru cazul particular al unei pietre aruncata la o inaltime relativ mica diferenta este nesemnificativa.

virgil a scris:Soarele rasare de la rasarit, deci pamantul se roteste dinspre vest spre est. Asta inseamna ca piatra aruncata ramane in urma locului de aruncare, adica deviata spre vest. Pentru calculul exact trebuie sa cunosti pozitia pe meridianul locului de aruncare, cu ajutorul caruia trebuie sa calculezi raza cercului paralelei Pamantului, din punctul de aruncare (adica distanta de la punctul de aruncare pana la axa de rotatie a Pamantului, care este mai mica decat raza sferei pamantului.) Cunoscand aceasta distanta se poate afla viteza periferica a Pamantului la locul de aruncare, stiind ca viteza periferica este maxima la ecuator si zero la poli, in timp ce viteza unghiulara este aceiasi. Apoi cunoscand inaltimea h la care aruncam piatra se poate calcula folosind relatiile scrise anterior care este arcul de cerc descris de locul de aruncare, si arcul de cerc descris de punctul de inaltime maxima al pietrei. Desigur timpul de urcare se insumeaza cu timpul de coborare. Vom avea doua viteze periferice si un acelasi timp. Inmultindu-le vom gasi doua lungimi a caror diferenta ne arata cu cat ramane in urma piatra, la cadere fata de locul de lansare. Dar pentru cazul particular al unei pietre aruncata la o inaltime relativ mica diferenta este nesemnificativa.

Dacu a scris:
Eu cred că piatra este deviată spre vest la urcare tot atât de mult cât este deviată spre est la coborâre și deci în final piatra va reveni în același punct de unde a fost lansată iar traiectoria pietrei face parte dintr-o dreaptă.
Ce asemănare și ce deosebire este între "O exceptionala problema inca nerezolvata" și Pendulul lui Foucault?

virgil_48 a scris:

Dacu a scris:
Eu cred că piatra este deviată spre vest la urcare tot atât de mult cât este deviată spre est la coborâre și deci în final piatra va reveni în același punct de unde a fost lansată iar traiectoria pietrei face parte dintr-o dreaptă.
Ce asemănare și ce deosebire este între "O exceptionala problema inca nerezolvata" și Pendulul lui Foucault?

Dacule, cred ca acesta solutie, pe care am sustinut-o amândoi cu
exprimari oarecum diferite, nu poate fi respinsa.
Dar întrebarea "exceptionalei probleme" era ce curbura are traiectoria
(urcarii si caderii). Eu ma tot gândesc la o parabola, dar nu poate fi.
In punctul de la sol curba trebuie sa aiba tangentele verticale ! Sau
numai in cazul urcarii ? Cele doua traiectorii vor fi complet identice ?
Vezi daca ii poti determina functia, ca eu nici nu incerc.        

Dacu a scris:. . . . .
Nu cred că trebuie calculat nimic și deci eu cred că este o dreaptă care oscilează precum oscilează pendulul lui Foucault și de aceea am întrebat "Ce asemănare și ce deosebire este între "O exceptionala problema inca nerezolvata" și Pendulul lui Foucault?"...

virgil_48 a scris:

Dacu a scris:. . . . .
Nu cred că trebuie calculat nimic și deci eu cred că este o dreaptă care oscilează precum oscilează pendulul lui Foucault și de aceea am întrebat "Ce asemănare și ce deosebire este între "O exceptionala problema inca nerezolvata" și Pendulul lui Foucault?"...

Credeam ca ai glumit ! Nu ma bag, fiindca nu imi miroase bine.
Dar daca ai ceva de relevat, este un forum bun si pentru raspunsuri,
nu numai pentru intrebari.

Dacu a scris:. . . . .
Am răspuns că eu cred că traiectoria pietrei este o dreaptă care oscilează precum oscilează pendulul lui Foucault până ajunge în același punct de unde a fost lansată.  

virgil_48 a scris:

Dacu a scris:. . . . .
Am răspuns că eu cred că traiectoria pietrei este o dreaptă care oscilează precum oscilează pendulul lui Foucault până ajunge în același punct de unde a fost lansată.  

Nu poate fi dreapta dacule, fiindca componenta verticala a
miscarii nu este uniforma ci este uniform decelerata si apoi
accelerata. De gravitatie. Acolo este o curba sau sunt doua.

virgil a scris:Nu are nici o legatura cu pendulul, deoarece in cazul pietrei aruncate nu avem o oscilatie completa ci doar o frantura de oscilatie. O oscilatie completa ar fi daca exista un tunel prin centrul Pamantului ca sa iasa piatra pe partea cealalta astfel incat sa oscileze complet in campul gravitational.