Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Forever_Man Ieri la 22:56
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la virgil în Fiinte deosebite.
( 1 )
» Mesaj de la virgil în Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
( 1 )
» Mesaj de la CAdi în Sa mai auzim si de bine in Romania :
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12458) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Spune şi altora
Cine este conectat?
În total sunt 26 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 26 Vizitatori Nici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Curbura este egală cu torsiunea
+2
virgil_48
Abel Cavaşi
6 participanți
Pagina 1 din 4
Pagina 1 din 4 • 1, 2, 3, 4 
 Curbura este egală cu torsiunea
Curbura este egală cu torsiunea
Încerc să vă răspund aici la toate întrebările pe care mi le-ați pus în altă parte pe forum. Poate că din acest articol veți reuși să culegeți răspunsurile pe care n-am reușit încă să vi le ofer.
Recent, studiind cu Maxima graficele variațiilor curburii și ale torsiunii am avut o revelație crucială în Fizica elicoidală, care îmi clarifică multe aspecte ce nu se lăsau încă înțelese. Mai exact, am descoperit că un corp liber se mișcă, nu doar pe o elice circulară obișnuită, ci pe o elice care are ceva mai special în ea și anume curbura ei este egală cu torsiunea în valoare absolută.
Dar să vă spun mai exact despre ce este vorba. Să luăm un exemplu mai simplu, pentru început. Cred că puteți fi de acord cu faptul că un corp care este constrâns cumva să se miște pe un cerc va avea energie (potențială) mai mare decât același corp lăsat în pace care nu este constrâns să se miște pe cerc. Deci, cu cât curbura cercului va fi mai mare (raza cercului mai mică), cu atât corpul deține mai multă energie potențială. Dar și reciproc, cu cât corpul deține (pentru că este constrâns să dețină) mai multă energie potențială, cu atât cercul pe care a fost constrâns să se deplaseze va avea o curbură mai mare. Așadar, trecerea de la un cerc de curbură mică la un cerc de curbură mai mare se realizează cu lucru mecanic efectuat asupra corpului și absorbție de energie, iar trecerea inversă de la rază mică la rază mare are loc cu degajare de energie și efectuare de lucru mecanic asupra mediului înconjurător.
Ei bine, așa cum am mai scris de multe ori pe blog, acest raționament este înglobat într-un postulat îndrăzneț al Fizicii elicoidale, postulat care, implicând constanta lui Planck, concretizează cantitativ relația dintre energia potențială a unui corp și forma traiectoriei sale. Este îndrăzneț deoarece afirmă că întreaga masă a unui corp se datorează numai și numai formei traiectoriei sale, ori aceasta este o noutate absolută în Fizică.
Relația de care vorbesc și pe care am mai prezentat-o, dar mai brutal, mai neintuitiv, mai lipsită de context decât acum, recunosc, este
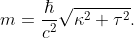
Această relație ne spune că cu cât curbura și torsiunea
și torsiunea 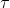 a traiectoriei pe care se deplasează un corp sunt mai mari, cu atât corpul va fi mai masiv, mai energic, respectiv, cu cât corpul este mai ușor, cu atât se deplasează pe traiectorii mai simple.
a traiectoriei pe care se deplasează un corp sunt mai mari, cu atât corpul va fi mai masiv, mai energic, respectiv, cu cât corpul este mai ușor, cu atât se deplasează pe traiectorii mai simple.
Sper ca măcar acum să vedeți această relație cu alți ochi, mai limpezi. Ea ne mai spune printre altele că curbura și torsiunea însele au inerție, adică nu le place să fie schimbate ușor, mai ales atunci când ele sunt mari.
Acum, dacă exemplul cu cercul, o curbă plană, deci cu torsiunea nulă, a fost dat doar în spirit didactic, pentru ca tinerii mei cititori să înțeleagă începutul relației dintre energia unui corp și forma traiectoriei sale, voi reveni la curba cea mai completă, care nu are doar curbură nenulă (precum are cercul), ci are și torsiune nenulă și, mai mult de-atât, este și cea mai simplă curbă cu aceste proprietăți: elicea.
Ei bine, atunci un corp liber care duce totuși cu el energie (caz în care corpul nu este absolut liber din moment ce este constrâns să transporte energie) se va mișca pe o elice a cărei formă ne vorbește despre câtă energie duce corpul respectiv.
Astfel, dacă i-am pus acelui corp în cârcă un sac cu energie, el se va deplasa la nesfârșit, bietul, de unul singur, prin Univers, pe o elice perfect circulară și nederanjată de nimic, a căror curbură și torsiune vor depinde de câtă energie l-am obligat pe bietul corp să ducă cu el. Mișcarea trebuie să fie în echilibru stabil.
Dar, de aici încolo lucrurile devin și mai interesante pentru că ne putem pune problema privind alegerea concretă pe care o va face corpul în ceea ce privește curbura și torsiunea elicei pe care să se deplaseze. Dilema corpului este dacă să se deplaseze pe o elice cu curbura mare și torsiunea mică sau pe o elice cu curbura mică și torsiunea mare. Relația dată mai sus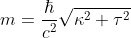 ne permite libertatea să alegem ce curbură dorim și ce torsiune dorim, cu condiția ca suma pătratelor lor să fie aceeași.
ne permite libertatea să alegem ce curbură dorim și ce torsiune dorim, cu condiția ca suma pătratelor lor să fie aceeași.
Așadar, când se obține echilibrul stabil? Ce curbură va alege corpul în mișcarea sa? Va alege oare corpul să se deplaseze pe un cerc, dând astfel toată energia sa curburii și neglijând torsiunea? Ar fi o asemenea mișcare în echilibru stabil? Nu s-ar supăra oare torsiunea în acest caz? Eu, dacă aș fi torsiune, în acest caz, m-aș revolta și i-aș reproșa corpului că favorizează curbura, deși curbura n-ar trebui să fie cu nimic mai presus decât mine. Așadar, corpul ar trebui să decidă corect între a împăca și capra și varza, fără ca acestea să se mai certe vreodată în infinitatea de timp în care corpul trebuie să-și ducă crucea.
În absența matematicii, ar trebui să ne mulțumim cu un astfel de raționament filozofic, raționament care ne duce la concluzia că dilema corpului se rezolvă prin mișcarea sa pe o elice având curbura egală cu torsiunea. Din fericire, matematica vine să întărească acest raționament filozofic. Și să vedem cum.
Se știe că curbura elicei este dată de formula
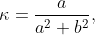
iar torsiunea este
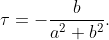
Iată și graficele, realizate cu Maxima, care exprimă curbura în funcție de raza elicei (la un anumit pas).
Curba albastră exprimă cum variază curbura când pasul este 3, curba roșie arată cum variază curbura când pasul este 4, iar curba verde arată cum variază curbura când pasul este 5.
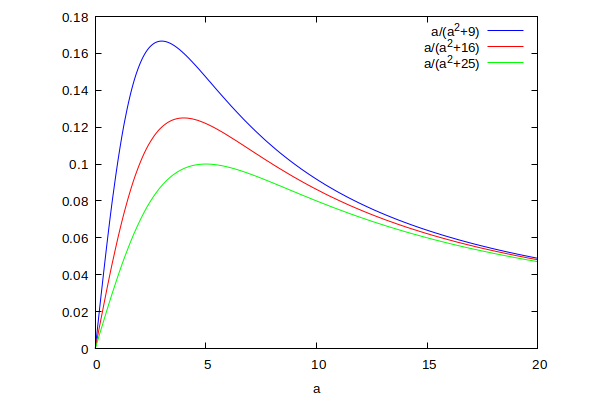
Și mai jos aveți graficul torsiunii, în aceleași culori ca și în cazul curburii.
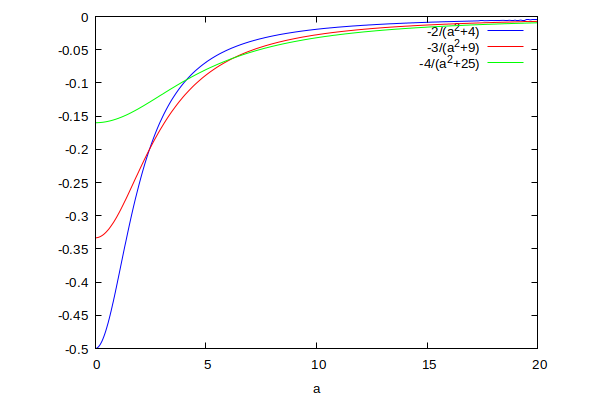
Pentru a înțelege profunzimea informației transmise de aceste grafice, vom face niște calcule.
Derivând curbura în funcție de raza a și presupunând că pasul b rămâne constant,
-2a\dot a}{(a^2+b^2)^2},)
deci obținem minunea asta de formulă:
^2}\dot a})
Ei bine, știți ce ne spune această minune de formulă? Că variația curburii este mai mititică atunci când numărătorul fracției de mai sus este mititel, adică atunci când diferența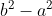 este cât de mică se poate, adică atunci când curbura este egală cu torsiunea în valoare absolută.
este cât de mică se poate, adică atunci când curbura este egală cu torsiunea în valoare absolută.
Și cum interpretăm atunci această formulă? Astfel: corpurile se deplasează mai liniștit, în echilibru mai stabil, atunci când curbura traiectoriei lor este egală cu torsiunea sau cu minus torsiunea, pentru că atunci variația curburii este mai mică. Corpurilor libere nu le plac variațiile, nu le place să fie deranjate, așa că vor evita variațiile, deci vor căuta să se deplaseze pe o asemenea traiectorie încât curbura să fie egală cu torsiunea.
Observați și pe grafic. Pe măsură ce raza elicei crește, crește și curbura, crește și torsiunea. Torsiunea crește pentru că este negativă, dar valoarea ei absolută scade, de fapt, elicea apropiindu-se de o curbă din ce în ce mai plană.
Însă, observați vârful graficului curburii. Pe măsură ce raza elicei crește, curbura crește și ea până când ajunge la un vârf în care variația ei dispare. Aici se obține valoarea maximă a curburii. Curbura este maximă și nu mai variază când raza elicei este egală cu pasul acesteia. Aici se obține acel mult dorit echilibru stabil al corpului, în care nu mai există variații ale energiei.
Dincolo de acest vârf curbura elicei începe să scadă pe măsură ce crește raza elicei, întocmai cum scade curbura cercului pe măsură ce crește raza lui. Deci, dincolo de acest vârf, elicea începe să devină din ce în ce mai asemănătoare cu un cerc. De asemenea, aproape de vârf variațiile curburii sunt insesizabile, chiar dacă variațiile razei ar fi mari, deci în vecinătatea vârfului stabilitatea este asigurată.
Mai mult, în lumina acestor considerații, se poate spune că, așa cum există condensatoare electrice care pot îngloba cât mai multă energie electrică într-o anumită formă, tot astfel, elicea însăși este și ea un „condensator” de energie care „înghite” mai multă energie atunci când curbura este mai apropiată de torsiune în valoare absolută. Astfel, corpurile în care s-a pompat energie și care au fost obligate să conțină cât mai multă energie, vor face cumva să se miște pe o elice având raza cât mai apropiată de pas. Dacă vom micșora raza elicei, energia corpului va fi din ce în ce mai mare, dar numai dacă nu micșorăm prea mult raza elicei. Căci dacă micșorăm raza mai mult decât pasul, atunci curbura începe să scadă, iar capacitatea energetică a elicei scade și ea.
Iar de aici se deschide o nouă lume pentru noua Fizică. Țineți aproape! Cu pandemia asta am și eu, în sfârșit, timp să sap mai adânc în această Fizică elicoidală. Voi veni cu noutăți. Am de gând să vă mai vorbesc despre asemănarea acestor grafice cu acelea ale radiației corpului negru, despre interpretarea „clasică” a efectului fotoelectric, am de gând să vă vorbesc despre rezonanța orbitală a sateliților lui Jupiter, coroborat cu mișcarea electronilor în atom, despre legea Titius-bode, despre salturi cuantice, despre unda asociată particulelor, despre lichefierea gazelor, despre dezechilibrul dintre materie și antimaterie (antimateria are torsiunea pozitivă), despre turbulență, despre adevărata lege a gravitației, toate în contextul acesta fundamental determinat de mișcarea corpurilor pe elice circulare.
Am de gând să vă arăt că, pornind de la aceste premize fundamentale prezentate în articol, această Fizică nouă face legătura mult visată între Fizica corpurilor macroscopice (teoria gravitației) și Fizica corpurilor microscopice (Fizica cuantică), prima aflându-se acolo unde raza de curbură a elicei este foarte mare (în dreapta vârfului), iar a doua acolo unde raza este foarte mică (în stânga vârfului).
Nu ezitați să comentați, să întrebați, să adăugați, să criticați. Și nu ezitați să dați de veste, distribuind articolul, dacă v-a pus pe gânduri. Mulțumesc!
Recent, studiind cu Maxima graficele variațiilor curburii și ale torsiunii am avut o revelație crucială în Fizica elicoidală, care îmi clarifică multe aspecte ce nu se lăsau încă înțelese. Mai exact, am descoperit că un corp liber se mișcă, nu doar pe o elice circulară obișnuită, ci pe o elice care are ceva mai special în ea și anume curbura ei este egală cu torsiunea în valoare absolută.
Dar să vă spun mai exact despre ce este vorba. Să luăm un exemplu mai simplu, pentru început. Cred că puteți fi de acord cu faptul că un corp care este constrâns cumva să se miște pe un cerc va avea energie (potențială) mai mare decât același corp lăsat în pace care nu este constrâns să se miște pe cerc. Deci, cu cât curbura cercului va fi mai mare (raza cercului mai mică), cu atât corpul deține mai multă energie potențială. Dar și reciproc, cu cât corpul deține (pentru că este constrâns să dețină) mai multă energie potențială, cu atât cercul pe care a fost constrâns să se deplaseze va avea o curbură mai mare. Așadar, trecerea de la un cerc de curbură mică la un cerc de curbură mai mare se realizează cu lucru mecanic efectuat asupra corpului și absorbție de energie, iar trecerea inversă de la rază mică la rază mare are loc cu degajare de energie și efectuare de lucru mecanic asupra mediului înconjurător.
Ei bine, așa cum am mai scris de multe ori pe blog, acest raționament este înglobat într-un postulat îndrăzneț al Fizicii elicoidale, postulat care, implicând constanta lui Planck, concretizează cantitativ relația dintre energia potențială a unui corp și forma traiectoriei sale. Este îndrăzneț deoarece afirmă că întreaga masă a unui corp se datorează numai și numai formei traiectoriei sale, ori aceasta este o noutate absolută în Fizică.
Relația de care vorbesc și pe care am mai prezentat-o, dar mai brutal, mai neintuitiv, mai lipsită de context decât acum, recunosc, este
Această relație ne spune că cu cât curbura
Sper ca măcar acum să vedeți această relație cu alți ochi, mai limpezi. Ea ne mai spune printre altele că curbura și torsiunea însele au inerție, adică nu le place să fie schimbate ușor, mai ales atunci când ele sunt mari.
Acum, dacă exemplul cu cercul, o curbă plană, deci cu torsiunea nulă, a fost dat doar în spirit didactic, pentru ca tinerii mei cititori să înțeleagă începutul relației dintre energia unui corp și forma traiectoriei sale, voi reveni la curba cea mai completă, care nu are doar curbură nenulă (precum are cercul), ci are și torsiune nenulă și, mai mult de-atât, este și cea mai simplă curbă cu aceste proprietăți: elicea.
Ei bine, atunci un corp liber care duce totuși cu el energie (caz în care corpul nu este absolut liber din moment ce este constrâns să transporte energie) se va mișca pe o elice a cărei formă ne vorbește despre câtă energie duce corpul respectiv.
Astfel, dacă i-am pus acelui corp în cârcă un sac cu energie, el se va deplasa la nesfârșit, bietul, de unul singur, prin Univers, pe o elice perfect circulară și nederanjată de nimic, a căror curbură și torsiune vor depinde de câtă energie l-am obligat pe bietul corp să ducă cu el. Mișcarea trebuie să fie în echilibru stabil.
Dar, de aici încolo lucrurile devin și mai interesante pentru că ne putem pune problema privind alegerea concretă pe care o va face corpul în ceea ce privește curbura și torsiunea elicei pe care să se deplaseze. Dilema corpului este dacă să se deplaseze pe o elice cu curbura mare și torsiunea mică sau pe o elice cu curbura mică și torsiunea mare. Relația dată mai sus
Așadar, când se obține echilibrul stabil? Ce curbură va alege corpul în mișcarea sa? Va alege oare corpul să se deplaseze pe un cerc, dând astfel toată energia sa curburii și neglijând torsiunea? Ar fi o asemenea mișcare în echilibru stabil? Nu s-ar supăra oare torsiunea în acest caz? Eu, dacă aș fi torsiune, în acest caz, m-aș revolta și i-aș reproșa corpului că favorizează curbura, deși curbura n-ar trebui să fie cu nimic mai presus decât mine. Așadar, corpul ar trebui să decidă corect între a împăca și capra și varza, fără ca acestea să se mai certe vreodată în infinitatea de timp în care corpul trebuie să-și ducă crucea.
În absența matematicii, ar trebui să ne mulțumim cu un astfel de raționament filozofic, raționament care ne duce la concluzia că dilema corpului se rezolvă prin mișcarea sa pe o elice având curbura egală cu torsiunea. Din fericire, matematica vine să întărească acest raționament filozofic. Și să vedem cum.
Se știe că curbura elicei este dată de formula
iar torsiunea este
Iată și graficele, realizate cu Maxima, care exprimă curbura în funcție de raza elicei (la un anumit pas).
Curba albastră exprimă cum variază curbura când pasul este 3, curba roșie arată cum variază curbura când pasul este 4, iar curba verde arată cum variază curbura când pasul este 5.

Și mai jos aveți graficul torsiunii, în aceleași culori ca și în cazul curburii.

Pentru a înțelege profunzimea informației transmise de aceste grafice, vom face niște calcule.
Derivând curbura în funcție de raza a și presupunând că pasul b rămâne constant,
deci obținem minunea asta de formulă:
Ei bine, știți ce ne spune această minune de formulă? Că variația curburii este mai mititică atunci când numărătorul fracției de mai sus este mititel, adică atunci când diferența
Și cum interpretăm atunci această formulă? Astfel: corpurile se deplasează mai liniștit, în echilibru mai stabil, atunci când curbura traiectoriei lor este egală cu torsiunea sau cu minus torsiunea, pentru că atunci variația curburii este mai mică. Corpurilor libere nu le plac variațiile, nu le place să fie deranjate, așa că vor evita variațiile, deci vor căuta să se deplaseze pe o asemenea traiectorie încât curbura să fie egală cu torsiunea.
Observați și pe grafic. Pe măsură ce raza elicei crește, crește și curbura, crește și torsiunea. Torsiunea crește pentru că este negativă, dar valoarea ei absolută scade, de fapt, elicea apropiindu-se de o curbă din ce în ce mai plană.
Însă, observați vârful graficului curburii. Pe măsură ce raza elicei crește, curbura crește și ea până când ajunge la un vârf în care variația ei dispare. Aici se obține valoarea maximă a curburii. Curbura este maximă și nu mai variază când raza elicei este egală cu pasul acesteia. Aici se obține acel mult dorit echilibru stabil al corpului, în care nu mai există variații ale energiei.
Dincolo de acest vârf curbura elicei începe să scadă pe măsură ce crește raza elicei, întocmai cum scade curbura cercului pe măsură ce crește raza lui. Deci, dincolo de acest vârf, elicea începe să devină din ce în ce mai asemănătoare cu un cerc. De asemenea, aproape de vârf variațiile curburii sunt insesizabile, chiar dacă variațiile razei ar fi mari, deci în vecinătatea vârfului stabilitatea este asigurată.
Mai mult, în lumina acestor considerații, se poate spune că, așa cum există condensatoare electrice care pot îngloba cât mai multă energie electrică într-o anumită formă, tot astfel, elicea însăși este și ea un „condensator” de energie care „înghite” mai multă energie atunci când curbura este mai apropiată de torsiune în valoare absolută. Astfel, corpurile în care s-a pompat energie și care au fost obligate să conțină cât mai multă energie, vor face cumva să se miște pe o elice având raza cât mai apropiată de pas. Dacă vom micșora raza elicei, energia corpului va fi din ce în ce mai mare, dar numai dacă nu micșorăm prea mult raza elicei. Căci dacă micșorăm raza mai mult decât pasul, atunci curbura începe să scadă, iar capacitatea energetică a elicei scade și ea.
Iar de aici se deschide o nouă lume pentru noua Fizică. Țineți aproape! Cu pandemia asta am și eu, în sfârșit, timp să sap mai adânc în această Fizică elicoidală. Voi veni cu noutăți. Am de gând să vă mai vorbesc despre asemănarea acestor grafice cu acelea ale radiației corpului negru, despre interpretarea „clasică” a efectului fotoelectric, am de gând să vă vorbesc despre rezonanța orbitală a sateliților lui Jupiter, coroborat cu mișcarea electronilor în atom, despre legea Titius-bode, despre salturi cuantice, despre unda asociată particulelor, despre lichefierea gazelor, despre dezechilibrul dintre materie și antimaterie (antimateria are torsiunea pozitivă), despre turbulență, despre adevărata lege a gravitației, toate în contextul acesta fundamental determinat de mișcarea corpurilor pe elice circulare.
Am de gând să vă arăt că, pornind de la aceste premize fundamentale prezentate în articol, această Fizică nouă face legătura mult visată între Fizica corpurilor macroscopice (teoria gravitației) și Fizica corpurilor microscopice (Fizica cuantică), prima aflându-se acolo unde raza de curbură a elicei este foarte mare (în dreapta vârfului), iar a doua acolo unde raza este foarte mică (în stânga vârfului).
Nu ezitați să comentați, să întrebați, să adăugați, să criticați. Și nu ezitați să dați de veste, distribuind articolul, dacă v-a pus pe gânduri. Mulțumesc!
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Eroica determinarea ta de a demonstra ca ultimul lucru care ramasese
drept in lumea asta stramba, ma refer la miscarea rectilinie, nu exista.
Toate celelalte, timpul, conservarile, masa, viteza, gravitatia, infinitul,
le-au "facut praf" inaintasii. Se pare ca ataci reduta cea mai puternica,
unde ei nu au reusit, ca o desfiintau pana acum.
drept in lumea asta stramba, ma refer la miscarea rectilinie, nu exista.
Toate celelalte, timpul, conservarile, masa, viteza, gravitatia, infinitul,
le-au "facut praf" inaintasii. Se pare ca ataci reduta cea mai puternica,
unde ei nu au reusit, ca o desfiintau pana acum.
virgil_48- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 11380




Puncte : 44921
Data de inscriere : 03/12/2013
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Pune „mâna” și aprofundează ce am scris. Numai de câștigat vei avea. Este un teren nou, fertil, numai bun pentru noua cercetare.
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Eu iti urez sa gasesti un interlocutor cum iti doresti, mai pregatitAbel Cavaşi a scris:Încerc să vă răspund aici la toate întrebările pe care mi le-ați pus în altă parte pe forum. Poate că din acest articol veți reuși să culegeți răspunsurile pe care n-am reușit încă să vi le ofer.
Recent, studiind cu Maxima graficele variațiilor curburii și ale torsiunii am avut o revelație crucială în Fizica elicoidală, care îmi clarifică multe aspecte ce nu se lăsau încă înțelese. Mai exact, am descoperit că un corp liber se mișcă, nu doar pe o elice circulară obișnuită, ci pe o elice care are ceva mai special în ea și anume curbura ei este egală cu torsiunea în valoare absolută.
si mai receptiv ca mine(eu nu sunt!) pentru subiectul topicului tau.
Dar deocamdata, pana va veni acela, detaliaza putin cum poate
fi egala curbura cu torsiunea. Ca sa fie egale in valoare absoluta
nu ar trebui sa aiba aceeasi unitate de masura ?
Se raporteaza la aceeasi lungime parcursa? Eu nu inteleg aceasta
egalitate. Ce inseamna si cum se explica, mai intai in cuvinte.
Pe urma putem discuta si de amanunte, formule, etc.
Intentionez sa abordez succesiv fragmentele create de tine, fiindca
nu pot merge mai departe ignorand semnele de intrebare.
Daca teoria ta s-ar dovedi adevarata, ar trebui sa o poti explica
si elevilor, nu numai mie.
virgil_48- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 11380




Puncte : 44921
Data de inscriere : 03/12/2013
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Da, curbura și torsiunea au una și aceeași unitate de măsură: inversul unei distanțe. Deci pot fi și egale.
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Curbura este 1 / R, unde R este raza, masurata in plan.Abel Cavaşi a scris:Da, curbura și torsiunea au una și aceeași unitate de măsură: inversul unei distanțe. Deci pot fi și egale.
Este inversul UNEI distante. (Abordarea elementara!)
Dar o torsiune a unei curbe trebuie sa tina seama si de
pasul torsiunii, nu numai de raza . Ma refer pentru
simplificare la o torsiune uniforma.
In acest caz nu este vorba de DOUA distante ? Fiindca o
singura distanta(R), caracterizeaza numai o curba plana
iar torsiunea se petrece in spatiu.
Daca ai un cerc(in plan) pe care poti sa il intinzi ca pe un
resort(in spatiu), acesta in spatiu are o dimensiune in
plus.
virgil_48- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 11380




Puncte : 44921
Data de inscriere : 03/12/2013
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
virgil_48 a scris:Curbura este 1 / R, unde R este raza, masurata in plan.Abel Cavaşi a scris:Da, curbura și torsiunea au una și aceeași unitate de măsură: inversul unei distanțe. Deci pot fi și egale.
Este inversul UNEI distante. (Abordarea elementara!)
Dar o torsiune a unei curbe trebuie sa tina seama si de
pasul torsiunii, nu numai de raza . Ma refer pentru
simplificare la o torsiune uniforma.
In acest caz nu este vorba de DOUA distante ? Fiindca o
singura distanta(R), caracterizeaza numai o curba plana
iar torsiunea se petrece in spatiu.
Daca ai un cerc(in plan) pe care poti sa il intinzi ca pe un
resort(in spatiu), acesta in spatiu are o dimensiune in
plus.
Curbura se masoara in [1/m] iar torsiunea se masoara in [grad/m]
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Musai să adaugi ceva de la tine, înainte să înțelegi bine ceea ce au spus alții. Păi, vezi că ți-am dat acolo formula torsiunii. De acolo poți deduce unitatea de măsură.virgil_48 a scris:Dar o torsiune a unei curbe trebuie sa tina seama si de
pasul torsiunii, nu numai de raza .
Virgil, vezi că tu te referi la alt tip de torsiune, la cea din rezistența materialelor. Nu este totuna cu torsiunea curbelor.virgil a scris:torsiunea se masoara in [grad/m]
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Abel,
Se foloseste "corp", "traiectoria corpului", etc.
Cu cat coboram in micro, " corpurile" devin din ce in ce mai mici, pana la " lesajoni", daca am inteles bine ce vrei så spui prin lesajoni.
In micro curburile si torsiunile sunt foarte mari.
Banuiesc ca se poate nuanta termenul "corp".
Se foloseste "corp", "traiectoria corpului", etc.
Cu cat coboram in micro, " corpurile" devin din ce in ce mai mici, pana la " lesajoni", daca am inteles bine ce vrei så spui prin lesajoni.
In micro curburile si torsiunile sunt foarte mari.
Banuiesc ca se poate nuanta termenul "corp".
eugen- Moderator

- Mulţumit de forum : Numarul mesajelor : 3969




Puncte : 33345
Data de inscriere : 19/03/2010
Obiective curente : Ma intereseaza comportarea bobinelor in inalta frecventa, la care apar impedante capacitive proprii sporite, eliminarea lor, reducerea rezistentei peliculare, marirea inductantei unei bobine, condensatori de inalta capacitate, etc.
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Am o mare retinere de a incerca sa inteleg ce au spus altii. Si nuAbel Cavaşi a scris:Musai să adaugi ceva de la tine, înainte să înțelegi bine ceea ce au spus alții. Păi, vezi că ți-am dat acolo formula torsiunii. De acolo poți deduce unitatea de măsură.virgil_48 a scris:Dar o torsiune a unei curbe trebuie sa tina seama si de
pasul torsiunii, nu numai de raza .
am nici o intentie sa deduc ceva. Formula poate ai dat-o, dar se
plimba prin stiinta aceasta formule importante care au fost
acceptate din respect.
Cel care pretinde ca avut revelatii si a facut descoperiri, trebuie sa
fie foarte exigent, precaut si detaliat cu cercetarea sa.
Fiindca aici, pe forum, vei intalni numai cusurgii .
Mai ales ca mm nu se mai prezinta la apel.
Chiar daca torsiunea unei traiectorii nu este acelasi lucru cu ceaVirgil, vezi că tu te referi la alt tip de torsiune, la cea din rezistența materialelor. Nu este totuna cu torsiunea curbelor.virgil a scris:torsiunea se masoara in [grad/m]
din rezistenta materialelor, mi se pare ca se masoara asa cum
scrie in citat. Nu inteleg dece ar fi altfel.
Tu ce relatie propui pentru masurarea torsiunea unei miscari care
se roteste 360 o in jurul traiectoriei principale, avansand
1 m ? Nu 360o pe metru ? Daca nu, corecteaza-ma.
virgil_48- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 11380




Puncte : 44921
Data de inscriere : 03/12/2013
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Păi, înseamnă că dialogul cu tine este inutil din fașă.virgil_48 a scris:
Am o mare retinere de a incerca sa inteleg ce au spus altii. Si nu
am nici o intentie sa deduc ceva.
Eu mă refer la „corp” în general, indiferent ce-o fi el, că-i particulă elementară, că-i atom, că-i om, că-i planetă, că-i galaxie.eugen a scris:Abel,
Se foloseste "corp", "traiectoria corpului", etc.
Cu cat coboram in micro, " corpurile" devin din ce in ce mai mici, pana la " lesajoni", daca am inteles bine ce vrei så spui prin lesajoni.
In micro curburile si torsiunile sunt foarte mari.
Banuiesc ca se poate nuanta termenul "corp".
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Pentru a discuta despre curbura si torsiunea unei traiectorii avem nevoie de un sistem de coordonate fix (x,y,z) in care este descrisa traiectoria si de un sistem de coordonate mobil (x', y', z' ) atasat punctului care descrie traiectoria.
1.Acum sa consideram ca descriem o traiectorie circulara in jurul axei x, si vom vedea ca sistemul atasat punctului care descrie traiectoria se va roti pe un cerc cu raza R in jurul axei x pastrand tot timpul axele de coordonate ale punctului, paralele cu axele de coordonate ale sistemului fix. Acest lucru se petrece cand nu exista un camp central. Curbura traiectoriei va fi notata cu 1/R.
2 Dar aceiasi traiectorie circulara se poate trasa si in conditiile in care ne situam intr-un camp central, sistemul de coordonate mobil va avea axa x' paralela cu axa x, si axa y' orientata tot timpul pe directia razei vectoare ce descrie cercul. In acest caz putem spune ca sistemul mobil se rasuceste in jurul axei x' si a axei sistemului fix notata cu x. Si curbura acestei traiectorii este 1/R.
3.Daca vrem sa descriem o traiectorie liniara paralela cu axa x atunci sistemul mobil isi va pastra axele paralele cu sistemul fix deplasandu-se de-alungul axei x. In acest caz nu exista torsiune.
4.Sa incercam acum sa descriem o traiectorie liniara ce este caracterizata de torsiune. Sistemul atasat punctului care descrie traiectoria se va deplasa dealungul axei x pastrand axa x' paralela cu aceasta, dar efectuand o miscare de rotatie in jurul axei x', deci axele y' si z' vor descrie arii elicoidale circulare fata de sistemul fix.
5. Daca combinam miscarile de rotatie orientata de la punctul 2 cu miscarea de torsiune de la punctul 4, vom observa ca avem o miscare elicoidala in care sistemul de coordonate mobil se deplaseaza dealungul axei x avand axa x' paralela cu aceasta, dar se si roteste in jurul axei x avand tot timpul axa y' paralela cu raza vectoare ce descrie cercul.
Abia in aceasta ultima situatie putem vorbi de curbura 1/R si torsiunea data pe pasul elicoidei. Prin pasul elicoidei intelegand distanta parcursa de sistemul mobil dealungul axei x a sist. fix, intre doua pozitii succesive avand axa y' paralela cu axa y a sist. fix.
1.Acum sa consideram ca descriem o traiectorie circulara in jurul axei x, si vom vedea ca sistemul atasat punctului care descrie traiectoria se va roti pe un cerc cu raza R in jurul axei x pastrand tot timpul axele de coordonate ale punctului, paralele cu axele de coordonate ale sistemului fix. Acest lucru se petrece cand nu exista un camp central. Curbura traiectoriei va fi notata cu 1/R.
2 Dar aceiasi traiectorie circulara se poate trasa si in conditiile in care ne situam intr-un camp central, sistemul de coordonate mobil va avea axa x' paralela cu axa x, si axa y' orientata tot timpul pe directia razei vectoare ce descrie cercul. In acest caz putem spune ca sistemul mobil se rasuceste in jurul axei x' si a axei sistemului fix notata cu x. Si curbura acestei traiectorii este 1/R.
3.Daca vrem sa descriem o traiectorie liniara paralela cu axa x atunci sistemul mobil isi va pastra axele paralele cu sistemul fix deplasandu-se de-alungul axei x. In acest caz nu exista torsiune.
4.Sa incercam acum sa descriem o traiectorie liniara ce este caracterizata de torsiune. Sistemul atasat punctului care descrie traiectoria se va deplasa dealungul axei x pastrand axa x' paralela cu aceasta, dar efectuand o miscare de rotatie in jurul axei x', deci axele y' si z' vor descrie arii elicoidale circulare fata de sistemul fix.
5. Daca combinam miscarile de rotatie orientata de la punctul 2 cu miscarea de torsiune de la punctul 4, vom observa ca avem o miscare elicoidala in care sistemul de coordonate mobil se deplaseaza dealungul axei x avand axa x' paralela cu aceasta, dar se si roteste in jurul axei x avand tot timpul axa y' paralela cu raza vectoare ce descrie cercul.
Abia in aceasta ultima situatie putem vorbi de curbura 1/R si torsiunea data pe pasul elicoidei. Prin pasul elicoidei intelegand distanta parcursa de sistemul mobil dealungul axei x a sist. fix, intre doua pozitii succesive avand axa y' paralela cu axa y a sist. fix.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Si reciproc, daca nu remarci nici intrebarile elementare, care punAbel Cavaşi a scris:Păi, înseamnă că dialogul cu tine este inutil din fașă.virgil_48 a scris:
Am o mare retinere de a incerca sa inteleg ce au spus altii. Si nu
am nici o intentie sa deduc ceva.
. . . . .
la indoiala prezentarea ta triumfalista:
O atitudine mai rezervata privind "descoperirea" ta, ar fi apreciata.Tu ce relatie propui pentru masurarea torsiunea unei miscari care
se roteste 360o in jurul traiectoriei principale, avansand
1 m ? Nu 360o pe metru ? Daca nu, corecteaza-ma.
Fiindca tot omul este supus greselii.
virgil_48- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 11380




Puncte : 44921
Data de inscriere : 03/12/2013
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Ce propun eu:
O elicoida are doua curburi si o singura torsiune.
Cele doua curburi sunt:
1. Curbura traiectoriei principale. Adica a curbei din axul
elicoidei.
2. Curbura elicoidei in jurul axului sau.
Ne putem aventura cu gandul la elicoide si mai complicate,
ale caror axe principale descriu si ele niste elicoide.
Care curburi mai sunt egale cu torsiunile atunci ? Nu te-ai
referit macar la o elicoida simpla, care are axul principal
drept si pasul egal. Un resort sau un filet.
In acest caz cercetarea ta se confirma ?
O elicoida are doua curburi si o singura torsiune.
Cele doua curburi sunt:
1. Curbura traiectoriei principale. Adica a curbei din axul
elicoidei.
2. Curbura elicoidei in jurul axului sau.
Ne putem aventura cu gandul la elicoide si mai complicate,
ale caror axe principale descriu si ele niste elicoide.
Care curburi mai sunt egale cu torsiunile atunci ? Nu te-ai
referit macar la o elicoida simpla, care are axul principal
drept si pasul egal. Un resort sau un filet.
In acest caz cercetarea ta se confirma ?
virgil_48- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 11380




Puncte : 44921
Data de inscriere : 03/12/2013
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Elicoida are o singura curbura care se poate descompune in trei proiectii, din care doua pe doua plane perpendiculare, si una pe un plan care este tangent intr-un punct la curba . Astfel daca elicea are axa ox, pe un plan (y,o,z) se proiecteaza un cerc, pe planul (x,o,y) se proiecteaza o sinusoida, si pe planul tangent intr-un punct la curba elicei se proiecteaza un arc de parabola cred.virgil_48 a scris:Ce propun eu:
O elicoida are doua curburi si o singura torsiune.
Cele doua curburi sunt:
1. Curbura traiectoriei principale. Adica a curbei din axul
elicoidei.
2. Curbura elicoidei in jurul axului sau.
Ne putem aventura cu gandul la elicoide si mai complicate,
ale caror axe principale descriu si ele niste elicoide.
Care curburi mai sunt egale cu torsiunile atunci ? Nu te-ai
referit macar la o elicoida simpla, care are axul principal
drept si pasul egal. Un resort sau un filet.
In acest caz cercetarea ta se confirma ?
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
In comentariul tau initial, vorbesti despre energia potentiala a unui corp care se roteste."Cred că puteți fi de acord cu faptul că un corp care este constrâns cumva să se miște pe un cerc va avea energie (potențială) mai mare decât același corp lăsat în pace care nu este constrâns să se miște pe cerc."
Dar orice corp in miscare (indiferent ce miscare) poseda energie cinetica, pe cand energia potentiala este data de pozitia unui corp aflat in campul gravitational, si nu are legatura cu viteza de rotatie a corpului respectiv, ci doar de pozitia lui fata de centrul campului.
Dar orice corp in miscare (indiferent ce miscare) poseda energie cinetica, pe cand energia potentiala este data de pozitia unui corp aflat in campul gravitational, si nu are legatura cu viteza de rotatie a corpului respectiv, ci doar de pozitia lui fata de centrul campului.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Să înțeleg că contești ceva din ceea ce am spus? Eu n-am negat asta, ci doar am generalizat la orice cauză care ar produce curbarea.
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Daca vrei sa sustii ca o elicoida de grad superior are o singuravirgil a scris:. . . . .
Elicoida are o singura curbura care se poate descompune in trei proiectii, din care doua pe doua plane perpendiculare, si una pe un plan care este tangent intr-un punct la curba . Astfel daca elicea are axa ox, pe un plan (y,o,z) se proiecteaza un cerc, pe planul (x,o,y) se proiecteaza o sinusoida, si pe planul tangent intr-un punct la curba elicei se proiecteaza un arc de parabola cred.
curbura, care se exprima analitic prin nu stiu ce ecuatii complicate,
ai castigat. Dar asta este numai un mod de a ascunde realitatea in
dosul teoriei si a hieroglifelor si de a o face inaccesibila majoritatii
celor curiosi. Boala cea veche ! Eu prefer sa le consider curburi
separate, care se compun, si care pot fi intelese fiecare cu rolul
sau. Dar cele doua moduri de abordare ar trebui sa duca in cele
din urma la acelasi rezultat.
virgil_48- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 11380




Puncte : 44921
Data de inscriere : 03/12/2013
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Curbarea unei sarme se obtine printr-o singura indoire in jurul unui contur dat de raza r. O elicoida o poti obtine rasucind acea sarma pe un cilindru, deci aplici o singura curbura, dupa care tragi de capetele sarmei si obtii elicoida cu o curbura oricat de mica. Deci pornesc de la o singura curbura maxima 1/r si torsiune zero , adica de la un cerc, apoi prin intindere se obtine orice curbura 1/R care tinde spre zero , deci curbura variaza intre 1/r si zero , care va fi insotita de torsiune, ce va fi cuprinsa intre zero (cerc) si pi/2 la sarma complet intinsa cand capetele sarmei nu-si schimba orientarea initiala.
Indiferent de cate spire (n) are sarma, torsiunea maxima finala va fi (n. pi/2 ) , incat torsiunea pe o spira va fi egala cu ( pi/2)
Astfel ca torsiunea variaza intre; 0 si (n.pi/2) pe toata lungimea elicoidei.
Indiferent de cate spire (n) are sarma, torsiunea maxima finala va fi (n. pi/2 ) , incat torsiunea pe o spira va fi egala cu ( pi/2)
Astfel ca torsiunea variaza intre; 0 si (n.pi/2) pe toata lungimea elicoidei.
Ultima editare efectuata de catre virgil in Mier 06 Mai 2020, 06:00, editata de 1 ori
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
negativ apreciază acest mesaj
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Cred că puteți fi de acord cu faptul că un corp care este constrâns cumva să se miște pe un cerc va avea energie (potențială) mai mare decât același corp lăsat în pace care nu este constrâns să se miște pe cerc."Abel Cavaşi a scris:Să înțeleg că contești ceva din ceea ce am spus? Eu n-am negat asta, ci doar am generalizat la orice cauză care ar produce curbarea.
Nu stiu daca Virgil va contesta sau nu citatul albastru, dar nu
inteleg despre ce energie potentiala este vorba. Un corp care se
misca are de obicei energie cinetica. Iar energia cinetica este
determinata de masa corpului si patratul vitezei instantanee.
Daca se misca rectiliniu sau se roteste, pentru aceeasi viteza,
intr-un anumit moment are aceeasi energie cinetica.
Daca nu o fi intervenit vreo modificare recenta.
virgil_48- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 11380




Puncte : 44921
Data de inscriere : 03/12/2013
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
virgil a scris:In comentariul tau initial, vorbesti despre energia potentiala a unui corp care se roteste."Cred că puteți fi de acord cu faptul că un corp care este constrâns cumva să se miște pe un cerc va avea energie (potențială) mai mare decât același corp lăsat în pace care nu este constrâns să se miște pe cerc."
Dar orice corp in miscare (indiferent ce miscare) poseda energie cinetica, pe cand energia potentiala este data de pozitia unui corp aflat in campul gravitational, si nu are legatura cu viteza de rotatie a corpului respectiv, ci doar de pozitia lui fata de centrul campului.
Eu am scris aici ce am avut de spus.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Nu asta facem toti ?virgil a scris:Eu am scris aici ce am avut de spus.virgil a scris:In comentariul tau initial, vorbesti despre energia potentiala a unui corp care se roteste.Cred că puteți fi de acord cu faptul că un corp care este constrâns cumva să se miște pe un cerc va avea energie (potențială) mai mare decât același corp lăsat în pace care nu este constrâns să se miște pe cerc.
Dar orice corp in miscare (indiferent ce miscare) poseda energie cinetica, pe cand energia potentiala este data de pozitia unui corp aflat in campul gravitational, si nu are legatura cu viteza de rotatie a corpului respectiv, ci doar de pozitia lui fata de centrul campului.
Iar citatul, chiar daca apare pe numele tau, cuprinde textul albastru
la care m-am referit si al carui autor este Abel.
Pentru acela este raspunsul meu anterior.
Nu am probleme cu raspunsul tau, te-am implicat involuntar.
virgil_48- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 11380




Puncte : 44921
Data de inscriere : 03/12/2013
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Exista o controversa intre termenul de elicoida si elice. In dex nu exista termenul de elicoida, ci doar de elicoid, care este o suprafata asemanatoare cu elicea de vapor sau cu o scara in spirala. Iata ca de exemplu in italiana elicoida poate insemna o curba stramba, sau o suprafata generata de aceasta curba.
Iata definitia la acesti termeni in italiana;
L’elica o elicoide è una curva sghemba percorsa da un punto che si muove secondo due moti uniformi simultanei: a) un moto circolare in un piano normale a un asse e b) un moto rettilineo parallelo all’asse stesso.
Un elicoide è una superficie generata da una linea generatrice che si muove di moto elicoidale intorno a un asse fisso: è chiuso quando la linea generatrice interseca l’asse, aperto in caso contrario.....
in traducere;
Helica sau elicoidul este o curbă înclinată parcursă de un punct care se mișcă în conformitate cu două mișcări uniforme simultane: a) o mișcare circulară într-un plan
Un helicoid este o suprafață generată de o linie generatoare care se deplasează elicoidal în jurul unei axe fixe: este închisă când linia generatoare intersectează axa, se deschide altfel....
Iata definitia la acesti termeni in italiana;
L’elica o elicoide è una curva sghemba percorsa da un punto che si muove secondo due moti uniformi simultanei: a) un moto circolare in un piano normale a un asse e b) un moto rettilineo parallelo all’asse stesso.
Un elicoide è una superficie generata da una linea generatrice che si muove di moto elicoidale intorno a un asse fisso: è chiuso quando la linea generatrice interseca l’asse, aperto in caso contrario.....
in traducere;
Helica sau elicoidul este o curbă înclinată parcursă de un punct care se mișcă în conformitate cu două mișcări uniforme simultane: a) o mișcare circulară într-un plan
Un helicoid este o suprafață generată de o linie generatoare care se deplasează elicoidal în jurul unei axe fixe: este închisă când linia generatoare intersectează axa, se deschide altfel....
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Iesind putin din abstractul notiunilor, sa aruncam o privire asupra unei tornade in mediul fluid.

Miscarea complexa a unei molecule de fluid se poate descompune ( presupunem turbulentele nule) in rotatii si translatii.
Fata de axa tornadei , o molecula e supusa la forte centrifuge si centripete.
Forta centripeta e data de presiunea exterioara spre ax, unde e tendinta de vacuumare.
Inteleg de exemplu energia potentiala a unei molecule in rotatie, ca energia primita de molecula daca molecula ar fi libera sa circule dinspre exterior spre ax, ca efect de "gravitatie " aparenta.

Miscarea complexa a unei molecule de fluid se poate descompune ( presupunem turbulentele nule) in rotatii si translatii.
Fata de axa tornadei , o molecula e supusa la forte centrifuge si centripete.
Forta centripeta e data de presiunea exterioara spre ax, unde e tendinta de vacuumare.
Inteleg de exemplu energia potentiala a unei molecule in rotatie, ca energia primita de molecula daca molecula ar fi libera sa circule dinspre exterior spre ax, ca efect de "gravitatie " aparenta.
Ultima editare efectuata de catre eugen in Mier 06 Mai 2020, 10:35, editata de 1 ori
eugen- Moderator

- Mulţumit de forum : Numarul mesajelor : 3969




Puncte : 33345
Data de inscriere : 19/03/2010
Obiective curente : Ma intereseaza comportarea bobinelor in inalta frecventa, la care apar impedante capacitive proprii sporite, eliminarea lor, reducerea rezistentei peliculare, marirea inductantei unei bobine, condensatori de inalta capacitate, etc.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Eu vorbesc de energie POTENȚIALĂ, nu cinetică. Nu neg că are aceeași energie cinetică, ci că are aceeași energie potențială.virgil_48 a scris:Cred că puteți fi de acord cu faptul că un corp care este constrâns cumva să se miște pe un cerc va avea energie (potențială) mai mare decât același corp lăsat în pace care nu este constrâns să se miște pe cerc."Abel Cavaşi a scris:Să înțeleg că contești ceva din ceea ce am spus? Eu n-am negat asta, ci doar am generalizat la orice cauză care ar produce curbarea.
Nu stiu daca Virgil va contesta sau nu citatul albastru, dar nu
inteleg despre ce energie potentiala este vorba. Un corp care se
misca are de obicei energie cinetica. Iar energia cinetica este
determinata de masa corpului si patratul vitezei instantanee.
Daca se misca rectiliniu sau se roteste, pentru aceeasi viteza,
intr-un anumit moment are aceeasi energie cinetica.
Daca nu o fi intervenit vreo modificare recenta.
Și așa vrei să mă convingi că elicea este același lucru cu elicoidul? Pune mâna pe o carte de mate, nu pe italiană.virgil a scris:Exista o controversa intre termenul de elicoida si elice. In dex nu exista termenul de elicoida, ci doar de elicoid, care este o suprafata asemanatoare cu elicea de vapor sau cu o scara in spirala. Iata ca de exemplu in italiana elicoida poate insemna o curba stramba, sau o suprafata generata de aceasta curba.
Iata definitia la acesti termeni in italiana;
L’elica o elicoide è una curva sghemba percorsa da un punto che si muove secondo due moti uniformi simultanei: a) un moto circolare in un piano normale a un asse e b) un moto rettilineo parallelo all’asse stesso.
Un elicoide è una superficie generata da una linea generatrice che si muove di moto elicoidale intorno a un asse fisso: è chiuso quando la linea generatrice interseca l’asse, aperto in caso contrario.....
in traducere;
Helica sau elicoidul este o curbă înclinată parcursă de un punct care se mișcă în conformitate cu două mișcări uniforme simultane: a) o mișcare circulară într-un plan
Un helicoid este o suprafață generată de o linie generatoare care se deplasează elicoidal în jurul unei axe fixe: este închisă când linia generatoare intersectează axa, se deschide altfel....
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Tu incercai sa demonstrezi ca miscarea LIBERA este elicoidala.Abel Cavaşi a scris:Eu vorbesc de energie POTENȚIALĂ, nu cinetică. Nu neg că are aceeași energie cinetică, ci că are aceeași energie potențială.virgil_48 a scris:Cred că puteți fi de acord cu faptul că un corp care este constrâns cumva să se miște pe un cerc va avea energie (potențială) mai mare decât același corp lăsat în pace care nu este constrâns să se miște pe cerc."Abel Cavaşi a scris:Să înțeleg că contești ceva din ceea ce am spus? Eu n-am negat asta, ci doar am generalizat la orice cauză care ar produce curbarea.
Nu stiu daca Virgil va contesta sau nu citatul albastru, dar nu
inteleg despre ce energie potentiala este vorba. Un corp care se
misca are de obicei energie cinetica. Iar energia cinetica este
determinata de masa corpului si patratul vitezei instantanee.
Daca se misca rectiliniu sau se roteste, pentru aceeasi viteza,
intr-un anumit moment are aceeasi energie cinetica.
Daca nu o fi intervenit vreo modificare recenta.
In miscarea libera, un corp nu are deloc energie potentiala.
Sau energia potentiala se confunda complet cu energia cinetica.
Alt potential il realizeaza numai gravitatia sau alt mijoc de
influentare. Ca sa devina circulara, miscarea este influenta de un
tirant sau alt mijloc. Elementul de "constrangere" amintit de tine.
Trebuie sa te hotatasti pana la urma carei miscari ii atribui. . . . . Mai exact, am descoperit că un corp liber se mișcă, nu doar pe o elice circulară obișnuită, ci pe o elice care are ceva mai special în ea și anume curbura ei este egală cu torsiunea în valoare absolută.
proprietatea de a fi elicoidala: celei libere sau celei fortate. Fiindca
invoci mereu factori exteriori si de mediu si incerci sa tragi
proprietati de la una la alta.
virgil_48- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 11380




Puncte : 44921
Data de inscriere : 03/12/2013
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Depinde cât de liberă. Dacă este atât de liberă încât corpul nu are nici măcar masă, atunci da, corpul se mișcă rectiliniu. Dar dacă este doar atât de liberă încât corpul are masă, atunci corpul se mișcă pe o elice ai cărei parametri depind de masa corpului (mai precis, masa depinde de parametrii traiectoriei).virgil_48 a scris:
Tu incercai sa demonstrezi ca miscarea LIBERA este elicoidala.
 Re: Curbura este egală cu torsiunea
Re: Curbura este egală cu torsiunea
Un corp in miscare rectilinie de fapt reprezinta un pachet de elicoide pentru fiecare microparticula din masa corpului cate una, avand toate elicoidele axele paralele cu traiectoria rectilinie a corpului. Deci desi corpul se deplaseaza rectiliniu, intreaga lui masa are o miscare elicoidala intrinseca. In aceasta discutie nu am luat in considerare miscarea elicoidala a corpului observat sa zicem in laborator, ca urmare a rotatiei Pamantului, sau a altor miscari cosmice.Abel Cavaşi a scris:Depinde cât de liberă. Dacă este atât de liberă încât corpul nu are nici măcar masă, atunci da, corpul se mișcă rectiliniu. Dar dacă este doar atât de liberă încât corpul are masă, atunci corpul se mișcă pe o elice ai cărei parametri depind de masa corpului (mai precis, masa depinde de parametrii traiectoriei).virgil_48 a scris:
Tu incercai sa demonstrezi ca miscarea LIBERA este elicoidala.
virgil- Moderator

- Mulţumit de forum : Prenume : Virgil




Numarul mesajelor : 12458
Puncte : 56972
Data de inscriere : 25/05/2010
Obiective curente : Deocamdată, ma preocupa o teorie a unificarii universale a interactiunii electromagnetice, gravitationale, cat si la niveluri de organizare inferioare acestora. Studiul similitudinii sistemelor micro si macrocosmice sta la baza teoriei unificarii universale.
Pagina 1 din 4 • 1, 2, 3, 4 
 Subiecte similare
Subiecte similare» Torsiunea totală
» Care (cât) este torsiunea unei drepte?
» De ce precesia Pământului este perpendiculară pe liniile de câmp, nu paralelă precum este cea a unui titirez?
» Care (cât) este torsiunea unei drepte?
» De ce precesia Pământului este perpendiculară pe liniile de câmp, nu paralelă precum este cea a unui titirez?
Pagina 1 din 4
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit