Curbura este egală cu torsiunea

Scris de **Abel Cavaşi** Mar 28 Apr 2020, 11:28

Rezumarea primului mesaj :

Încerc să vă răspund aici la toate întrebările pe care mi le-ați pus în altă parte pe forum. Poate că din acest articol veți reuși să culegeți răspunsurile pe care n-am reușit încă să vi le ofer.

Recent, studiind cu Maxima graficele variațiilor curburii și ale torsiunii am avut o revelație crucială în Fizica elicoidală, care îmi clarifică multe aspecte ce nu se lăsau încă înțelese. Mai exact, am descoperit că un corp liber se mișcă, nu doar pe o elice circulară obișnuită, ci pe o elice care are ceva mai special în ea și anume curbura ei este egală cu torsiunea în valoare absolută.

Dar să vă spun mai exact despre ce este vorba. Să luăm un exemplu mai simplu, pentru început. Cred că puteți fi de acord cu faptul că un corp care este constrâns cumva să se miște pe un cerc va avea energie (potențială) mai mare decât același corp lăsat în pace care nu este constrâns să se miște pe cerc. Deci, cu cât curbura cercului va fi mai mare (raza cercului mai mică), cu atât corpul deține mai multă energie potențială. Dar și reciproc, cu cât corpul deține (pentru că este constrâns să dețină) mai multă energie potențială, cu atât cercul pe care a fost constrâns să se deplaseze va avea o curbură mai mare. Așadar, trecerea de la un cerc de curbură mică la un cerc de curbură mai mare se realizează cu lucru mecanic efectuat asupra corpului și absorbție de energie, iar trecerea inversă de la rază mică la rază mare are loc cu degajare de energie și efectuare de lucru mecanic asupra mediului înconjurător.

Ei bine, așa cum am mai scris de multe ori pe blog, acest raționament este înglobat într-un postulat îndrăzneț al Fizicii elicoidale, postulat care, implicând constanta lui Planck, concretizează cantitativ relația dintre energia potențială a unui corp și forma traiectoriei sale. Este îndrăzneț deoarece afirmă că întreaga masă a unui corp se datorează numai și numai formei traiectoriei sale, ori aceasta este o noutate absolută în Fizică.

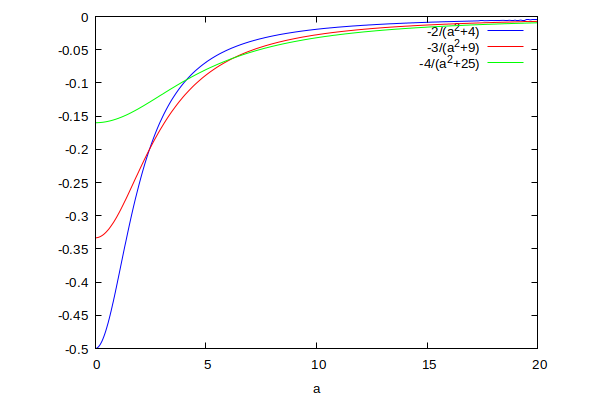
Relația de care vorbesc și pe care am mai prezentat-o, dar mai brutal, mai neintuitiv, mai lipsită de context decât acum, recunosc, este

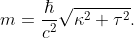
$Curbura este egală cu torsiunea - Pagina 4 Png.latex?m=\frac{\hbar}{c^2}\sqrt{\kappa^2+\tau^2}$

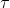Această relație ne spune că cu cât curbura $Curbura este egală cu torsiunea - Pagina 4 Png$ și torsiunea $Curbura este egală cu torsiunea - Pagina 4 Png$ a traiectoriei pe care se deplasează un corp sunt mai mari, cu atât corpul va fi mai masiv, mai energic, respectiv, cu cât corpul este mai ușor, cu atât se deplasează pe traiectorii mai simple.

Sper ca măcar acum să vedeți această relație cu alți ochi, mai limpezi. Ea ne mai spune printre altele că curbura și torsiunea însele au inerție, adică nu le place să fie schimbate ușor, mai ales atunci când ele sunt mari.

Acum, dacă exemplul cu cercul, o curbă plană, deci cu torsiunea nulă, a fost dat doar în spirit didactic, pentru ca tinerii mei cititori să înțeleagă începutul relației dintre energia unui corp și forma traiectoriei sale, voi reveni la curba cea mai completă, care nu are doar curbură nenulă (precum are cercul), ci are și torsiune nenulă și, mai mult de-atât, este și cea mai simplă curbă cu aceste proprietăți: elicea.

Ei bine, atunci un corp liber care duce totuși cu el energie (caz în care corpul nu este absolut liber din moment ce este constrâns să transporte energie) se va mișca pe o elice a cărei formă ne vorbește despre câtă energie duce corpul respectiv.

Astfel, dacă i-am pus acelui corp în cârcă un sac cu energie, el se va deplasa la nesfârșit, bietul, de unul singur, prin Univers, pe o elice perfect circulară și nederanjată de nimic, a căror curbură și torsiune vor depinde de câtă energie l-am obligat pe bietul corp să ducă cu el. Mișcarea trebuie să fie în echilibru stabil.

Dar, de aici încolo lucrurile devin și mai interesante pentru că ne putem pune problema privind alegerea concretă pe care o va face corpul în ceea ce privește curbura și torsiunea elicei pe care să se deplaseze. Dilema corpului este dacă să se deplaseze pe o elice cu curbura mare și torsiunea mică sau pe o elice cu curbura mică și torsiunea mare. Relația dată mai sus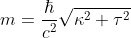 $Curbura este egală cu torsiunea - Pagina 4 Png$ ne permite libertatea să alegem ce curbură dorim și ce torsiune dorim, cu condiția ca suma pătratelor lor să fie aceeași.

Așadar, când se obține echilibrul stabil? Ce curbură va alege corpul în mișcarea sa? Va alege oare corpul să se deplaseze pe un cerc, dând astfel toată energia sa curburii și neglijând torsiunea? Ar fi o asemenea mișcare în echilibru stabil? Nu s-ar supăra oare torsiunea în acest caz? Eu, dacă aș fi torsiune, în acest caz, m-aș revolta și i-aș reproșa corpului că favorizează curbura, deși curbura n-ar trebui să fie cu nimic mai presus decât mine. Așadar, corpul ar trebui să decidă corect între a împăca și capra și varza, fără ca acestea să se mai certe vreodată în infinitatea de timp în care corpul trebuie să-și ducă crucea.

În absența matematicii, ar trebui să ne mulțumim cu un astfel de raționament filozofic, raționament care ne duce la concluzia că dilema corpului se rezolvă prin mișcarea sa pe o elice având curbura egală cu torsiunea. Din fericire, matematica vine să întărească acest raționament filozofic. Și să vedem cum.

Se știe că curbura elicei este dată de formula

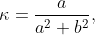
$Curbura este egală cu torsiunea - Pagina 4 Png$

iar torsiunea este

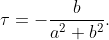
$Curbura este egală cu torsiunea - Pagina 4 Png.latex?\tau=-\frac{b}{a^2+b^2}$

Iată și graficele, realizate cu Maxima, care exprimă curbura în funcție de raza elicei (la un anumit pas).

Curba albastră exprimă cum variază curbura când pasul este 3, curba roșie arată cum variază curbura când pasul este 4, iar curba verde arată cum variază curbura când pasul este 5.

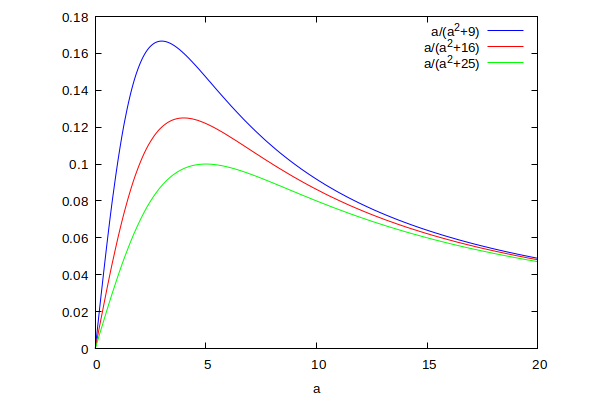
Curbura este egală cu torsiunea - Pagina 4 Variatia%2Bcurburii%2Bcu%2Bpas%2Bconstant

Și mai jos aveți graficul torsiunii, în aceleași culori ca și în cazul curburii.

Curbura este egală cu torsiunea - Pagina 4 Variatia%2Btorsiunii%2Bcu%2Bpas%2Bconstant

Pentru a înțelege profunzimea informației transmise de aceste grafice, vom face niște calcule.

Derivând curbura în funcție de raza a și presupunând că pasul b rămâne constant,
$Curbura este egală cu torsiunea - Pagina 4 Png$

deci obținem minunea asta de formulă:
$Curbura este egală cu torsiunea - Pagina 4 Png$

Ei bine, știți ce ne spune această minune de formulă? Că variația curburii este mai mititică atunci când numărătorul fracției de mai sus este mititel, adică atunci când diferența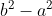 $Curbura este egală cu torsiunea - Pagina 4 Png$ este cât de mică se poate, adică atunci când curbura este egală cu torsiunea în valoare absolută.

Și cum interpretăm atunci această formulă? Astfel: corpurile se deplasează mai liniștit, în echilibru mai stabil, atunci când curbura traiectoriei lor este egală cu torsiunea sau cu minus torsiunea, pentru că atunci variația curburii este mai mică. Corpurilor libere nu le plac variațiile, nu le place să fie deranjate, așa că vor evita variațiile, deci vor căuta să se deplaseze pe o asemenea traiectorie încât curbura să fie egală cu torsiunea.

Observați și pe grafic. Pe măsură ce raza elicei crește, crește și curbura, crește și torsiunea. Torsiunea crește pentru că este negativă, dar valoarea ei absolută scade, de fapt, elicea apropiindu-se de o curbă din ce în ce mai plană.

Însă, observați vârful graficului curburii. Pe măsură ce raza elicei crește, curbura crește și ea până când ajunge la un vârf în care variația ei dispare. Aici se obține valoarea maximă a curburii. Curbura este maximă și nu mai variază când raza elicei este egală cu pasul acesteia. Aici se obține acel mult dorit echilibru stabil al corpului, în care nu mai există variații ale energiei.

Dincolo de acest vârf curbura elicei începe să scadă pe măsură ce crește raza elicei, întocmai cum scade curbura cercului pe măsură ce crește raza lui. Deci, dincolo de acest vârf, elicea începe să devină din ce în ce mai asemănătoare cu un cerc. De asemenea, aproape de vârf variațiile curburii sunt insesizabile, chiar dacă variațiile razei ar fi mari, deci în vecinătatea vârfului stabilitatea este asigurată.

Mai mult, în lumina acestor considerații, se poate spune că, așa cum există condensatoare electrice care pot îngloba cât mai multă energie electrică într-o anumită formă, tot astfel, elicea însăși este și ea un „condensator” de energie care „înghite” mai multă energie atunci când curbura este mai apropiată de torsiune în valoare absolută. Astfel, corpurile în care s-a pompat energie și care au fost obligate să conțină cât mai multă energie, vor face cumva să se miște pe o elice având raza cât mai apropiată de pas. Dacă vom micșora raza elicei, energia corpului va fi din ce în ce mai mare, dar numai dacă nu micșorăm prea mult raza elicei. Căci dacă micșorăm raza mai mult decât pasul, atunci curbura începe să scadă, iar capacitatea energetică a elicei scade și ea.

Iar de aici se deschide o nouă lume pentru noua Fizică. Țineți aproape! Cu pandemia asta am și eu, în sfârșit, timp să sap mai adânc în această Fizică elicoidală. Voi veni cu noutăți. Am de gând să vă mai vorbesc despre asemănarea acestor grafice cu acelea ale radiației corpului negru, despre interpretarea „clasică” a efectului fotoelectric, am de gând să vă vorbesc despre rezonanța orbitală a sateliților lui Jupiter, coroborat cu mișcarea electronilor în atom, despre legea Titius-bode, despre salturi cuantice, despre unda asociată particulelor, despre lichefierea gazelor, despre dezechilibrul dintre materie și antimaterie (antimateria are torsiunea pozitivă), despre turbulență, despre adevărata lege a gravitației, toate în contextul acesta fundamental determinat de mișcarea corpurilor pe elice circulare.

Am de gând să vă arăt că, pornind de la aceste premize fundamentale prezentate în articol, această Fizică nouă face legătura mult visată între Fizica corpurilor macroscopice (teoria gravitației) și Fizica corpurilor microscopice (Fizica cuantică), prima aflându-se acolo unde raza de curbură a elicei este foarte mare (în dreapta vârfului), iar a doua acolo unde raza este foarte mică (în stânga vârfului).

Nu ezitați să comentați, să întrebați, să adăugați, să criticați. Și nu ezitați să dați de veste, distribuind articolul, dacă v-a pus pe gânduri. Mulțumesc!

Scris de **gafiteanu** Vin 15 Mai 2020, 10:17

Pana se hotaraste Abel sa se debaneze, ii propun o pauza de
gandire pentru o situatie pe care i-am mai semnalat-o si care
nu a beneficiat de atentia lui in contextul acestui subiect:
Daca folosesti notiunea de CORP LIBER, acesta este sau nu
conectata biunivoc cu cea de MISCARE LIBERA ?
Notiunea de MISCARE LIBERA este conectata biunivoc cu
cea de SPATIU LIBER ?
Daca notiunea de spatiu liber nu o accepta ca facand parte din
realitatea fizica, o poate aborda in regim teoretic, imaginar.
Daca gaseste exemple ca relatiile anuntate de mine ca
biunivoce nu indeplinesc aceasta conditie, le astept.
Clarificarea relatiei din aceasta tripleta, ar fi punctul de plecare
pentru o discutie rationala si fara nervi, despre fizica elicoidala.
Am scris eu, virgil_48.

Scris de **virgil_48** Sam 16 Mai 2020, 08:04

Daca mai dura "legea martiala" poate ne lamuream si noi ce forma are
traiectoria unui corp liber si in ce fel de mediu poate avea loc. Dar asa,
clarificarea se amana pana la noi ordine. Poate vor afla raspunsul si vor
intelege rostul intrebarii urmasii nostri.
P.S. In primul rand vor trebui sa se lamureasca ce inseamna "corp liber".
Si sa inteleaga ca atunci cand spui "corp liber,"orice element de mediu
este o anulare a acelei libertati.

Scris de **virgil** Joi 23 Sept 2021, 15:30

12 definiții pentru torsiune

Dicționare explicative
Explică cele mai întâlnite sensuri ale cuvintelor.

TORSIÚNE, torsiuni, s. f. 1. Deplasare relativă a două secțiuni paralele și transversale ale unui obiect solid; răsucire.

Indice care arată gradul de torsiune (1) al unui material textil. 2. Scrântitură, luxație. [Pr.: -si-u-] – Din fr. torsion.

sursa: DEX '09 (2009) adăugată de blaurb. acțiuni
torsiune sf [At: MARIN, F. 373 / P: ~si-u~ / Pl: ~ni / E: fr torsion] 1 (Teh) Deplasare relativă a două secțiuni paralele și transversale ale unui obiect solid Si: răsucire. 2 (Med) Luxație. 3 Indice care arată gradul de torsiune (1) al unui material textil. 4 (Mat) Calitate caracteristică a curbelor (din spațiu).

sursa: MDA2 (2010) adăugată de blaurb. acțiuni
TORSIÚNE, torsiuni, s. f. 1. Deplasare relativă a două secțiuni paralele și transversale ale unui obiect solid în jurul unei axe, produsă prin acțiunea a două cupluri opuse, care acționează în planuri paralele; răsucire. Efort de torsiune. 2. Scrîntitură, răsucire. V. contorsiune. – Pronunțat: -si-u-.

sursa: DLRLC (1955-1957) adăugată de LauraGellner acțiuni
TORSIÚNE s.f. 1. Răsucire.

(Text.) Indice care arată gradul de torsionare a unui semitort, exprimat prin numărul de răsucituri pe unitatea de lungime. 2. (Mat.) Calitate caracteristică a curbelor (din spațiu). 3. Scrântitură, luxație. [Pron. -si-u-. / < fr. torsion, cf. lat. torsio < torquere – a răsuci].

sursa: DN (1986) adăugată de LauraGellner acțiuni
TORSIÚNE s. f. 1. răsucire. ◊ (text.) indice care arată gradul de torsiune a unui semitort, exprimat prin numărul de răsucituri pe unitatea de lungime. 2. (mat.) calitatea caracteristică a curbelor (din spațiu). 3. scrântitură, luxație. (< fr. torsion, lat. torsio)
ASA DAR DRAGI COLEGI ALINIATI-VA TEORIA LA TERMENII CONSACRATI !

Scris de **Abel Cavaşi** Joi 23 Sept 2021, 16:17

Iar curbele despre care vorbim aici (elice) au O SINGURĂ definiție a torsiunii, cea din primul mesaj al topicului.
Pune mâna pe carte și învață și nu mai face confuzii între noțiuni!

Scris de **virgil** Joi 23 Sept 2021, 17:22

Abel Cavaşi a scris:Iar curbele despre care vorbim aici (elice) au O SINGURĂ definiție a torsiunii, cea din primul mesaj al topicului.
Pune mâna pe carte și învață și nu mai face confuzii între noțiuni!

Invata tu, ca notiunile nemateriale precum traiectoriile, sunt lipsite de proprietatile corpurilor, asa ca ceia ce numesti tu si ceilalti teoreticieni "torsiune" trebuie sa-i schimbati denumirea in "pseudotorsiune". Limba romana spune foarte clar ce inseamna torsiunea.
Iar pseudotorsiunea reprezimta o marime care arata abaterea binormalei dealungul pasului elicei masurata intr-un plan determinat de raza de curbura si binormala. Dealungul unui pas al elicei, binormala sufera o rotire maxima de 2pi.

Curbura este egală cu torsiunea - Pagina 4 Triedr10

Scris de **eugen** Vin 24 Sept 2021, 00:04

Am senzatia ca matematica si dictionarul ne franeaza in a gandi fenomene reale.
Rigurozitatea definitiilor a contat putin in progresul tehnico-stiintific de exemplu, prin care am iesit din pestera la lumina.
Nu inteleg de ce atata inversunare de a folosi conventionalul.

Scris de **virgil_48** Vin 24 Sept 2021, 10:38

Abel Cavaşi a scris:Iar curbele despre care vorbim aici (elice) au O SINGURĂ definiție a torsiunii, cea din primul mesaj al topicului.
Pune mâna pe carte și învață și nu mai face confuzii între noțiuni!

Cu riscul de a ma trimite si pe mine la carte, cred ca tu acum
nu mai sustii acest topic si ai realizat singur ca titlul lui este o
eroare. Chiar daca n-am vazut o astfel de recunoastere la tine
pana acum.
O elice cu o anumita raza, poate avea pasul mic, asa cum
este un filet, sau de 1000 de ori mai mare.
Asa ca nu intrevad posibilitatea ca raza sa fie egala mereu cu
torsiunea.

Scris de **Abel Cavaşi** Vin 24 Sept 2021, 11:55

virgil_48 a scris:cred ca tu acum
nu mai sustii acest topic si ai realizat singur ca titlul lui este o
eroare. Chiar daca n-am vazut o astfel de recunoastere la tine
pana acum.
O elice cu o anumita raza, poate avea pasul mic, asa cum
este un filet, sau de 1000 de ori mai mare.
Asa ca nu intrevad posibilitatea ca raza sa fie egala mereu cu
torsiunea.

Nu-i așa că n-ai citit nimic din primul mesaj cu care am început topicul? Sau n-ai înțeles nimic din el. N-am spus nicăieri că o elice nu poate avea raza diferită de pas.

Mai exact, am descoperit că un corp liber se mișcă, nu doar pe o elice circulară obișnuită, ci pe o elice care are ceva mai special în ea și anume curbura ei este egală cu torsiunea în valoare absolută.

Cu ce tâmpenii îmi bat capul... Mare idiot sunt!

Scris de **virgil** Vin 24 Sept 2021, 15:20

eugen a scris:Am senzatia ca matematica si dictionarul ne franeaza in a gandi fenomene reale.
Rigurozitatea definitiilor a contat putin in progresul tehnico-stiintific de exemplu, prin care am iesit din pestera la lumina.
Nu inteleg de ce atata inversunare de a folosi conventionalul.

Eu nu vad de ce o asa mare inversunare ca sa adopti o proprietate specifica materialelor la o notiune imateriala cum este o traiectorie, la care sa atasezi niste relatii matematice care nu au nici o legatura cu realitatea.
De exemplu; Sa luam o elice circulara cu pasul de 10 cm si diametrul de 20 cm si sa-i calculati curbura si torsiunea cu relatiile date de Abel, apoi cu datele obtinute sa verificati relatia data de el; m=(h/2pi.c^2). (k^2 +to^2)^0,5 ;in care m este o masa, k este curbura, to este torsiunea h este constanta lui planck si c este viteza luminii.

Scris de **virgil_48** Sam 25 Sept 2021, 08:29

Trebuie sa intelegem de acum ca Abel incearca sa separe ideea
de torsiune geometrica de cea de torsiune a miscarii. Lupta
impotriva dreptei(geometrice) este o cauza pierduta din start.
A acceptat recent ca nu poate revolutiona si geometria, nu caut
citatul fiindca nu este nevoie.
Asa ca ar fi suficient sa ne clarifice in contextul acestui topic care
se numeste "Curbura este egala cu torsiunea", ce pas are miscarea
elicoidala care are raza de 10 cm. Daca exista acea egalitate si el
doreste sa o sustina pentru cazul miscarii, ar trebui sa existe un
raspuns in centimetri. r = 10 cm ; p = ?

Scris de **virgil** Sam 25 Sept 2021, 17:44

virgil a scris:
Abel Cavaşi a scris:Iar curbele despre care vorbim aici (elice) au O SINGURĂ definiție a torsiunii, cea din primul mesaj al topicului.
Pune mâna pe carte și învață și nu mai face confuzii între noțiuni!
Invata tu, ca notiunile nemateriale precum traiectoriile, sunt lipsite de proprietatile corpurilor, asa ca ceia ce numesti tu si ceilalti teoreticieni "torsiune" trebuie sa-i schimbati denumirea in "pseudotorsiune". Limba romana spune foarte clar ce inseamna torsiunea.
Iar pseudotorsiunea reprezimta o marime care arata abaterea binormalei dealungul pasului elicei masurata intr-un plan determinat de raza de curbura si binormala. Dealungul unui pas al elicei, binormala sufera o rotire maxima de 2pi.

Din moment ce intreg triedrul Frenet sufera o rotatie de 2pi dealungul unui pas al elicei, inseamna ca torsiunea reprezinta totdeauna pentru orice pas al elicei avem raportul ; To= 2pi/Pas ; (cu To s-a notat torsiunea). Asa ca daca pasul este zero elicea se reduce la un cerc pentru care rotatia axei este zero si pasul zero deci torsiunea este To=0/0 ; adica nedeterminat din punct de vedere matematic. Daca insa luam un calcul mai putin de un pas, de exemplu 1/2.pas torsiunea va fi; To=(1/2).2pi/pas =pi/pas ; iar daca luam in calcul "n" pasi
torsiunea va fi To=n.2pi/n.pas =2pi/pas. Daca rasucirea se masoara in grade, atunci torsiunea se va masura in [grade/m] respectiv 360/pasul elicei.

Scris de **virgil_48** Dum 26 Sept 2021, 09:50

Va bateti capul degeaba cu amanunte.

Recent, studiind cu Maxima graficele variațiilor curburii și ale torsiunii am avut o revelație crucială în Fizica elicoidală, care îmi clarifică multe aspecte ce nu se lăsau încă înțelese. Mai exact, am descoperit că un corp liber se mișcă, nu doar pe o elice circulară obișnuită, ci pe o elice care are ceva mai special în ea și anume curbura ei este egală cu torsiunea în valoare absolută.

Elicele speciale care directioneaza miscarea in conceptia lui Abel
trebuie sa aiba un raport determinat intre raza si pas. Aceste
caracteristici banale, luate din tehnica filetarii, ar putea clarifica
totul daca citatul ar fi adevarat. Fara alte batai de cap si teorii
speciale. Rezolvarile simple sunt cele mai sigure.
Dar Abel intarzie sa ne destainuie si noua aceasta legatura, ceace
ma face sa cred ca a renuntat deja la revelatia cruciala din
noaptea aceea.

Scris de **virgil** Dum 26 Sept 2021, 11:19

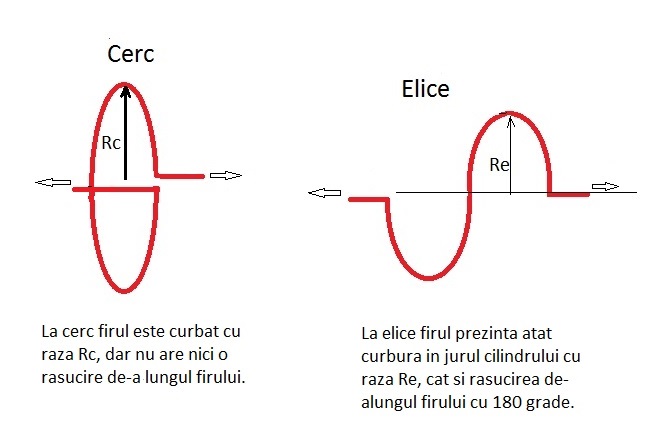
In poza aceasta se vede cum un cerc sectionat poate sa genereze o elice prin intindere pe o directie perpendiculara pe planul cercului.
Rasucirea firului elicei este de 180 grade sau pi radiani atunci cand firul este intins la maxim devenind o linie dreapta. Astfel ca rasucirea poate varia intre zero in cazul cercului si creste pe masura ce creste pasul elicei ajungand pana la 180 grade. Astfel torsiunea firului reprezinta raportul dintre rasucirea lui masurata in grade si lungimea cercului, sau a elicei desfasurate.

Curbura este egală cu torsiunea - Pagina 4 Elicea12

Scris de **virgil** Dum 26 Sept 2021, 20:02

Abel Cavaşi a scris:Încerc să vă răspund aici la toate întrebările pe care mi le-ați pus în altă parte pe forum. Poate că din acest articol veți reuși să culegeți răspunsurile pe care n-am reușit încă să vi le ofer.
Se știe că curbura elicei este dată de formula

$Curbura este egală cu torsiunea - Pagina 4 Png$

iar torsiunea este

$Curbura este egală cu torsiunea - Pagina 4 Png.latex?\tau=-\frac{b}{a^2+b^2}$

Nu ezitați să comentați, să întrebați, să adăugați, să criticați. Și nu ezitați să dați de veste, distribuind articolul, dacă v-a pus pe gânduri. Mulțumesc!

Scris de **virgil** Dum 26 Sept 2021, 20:16

Abel Cavaşi a scris:Încerc să vă răspund aici la toate întrebările pe care mi le-ați pus în altă parte pe forum. Poate că din acest articol veți reuși să culegeți răspunsurile pe care n-am reușit încă să vi le ofer.

Se știe că curbura elicei este dată de formula

$Curbura este egală cu torsiunea - Pagina 4 Png$

iar torsiunea este

$Curbura este egală cu torsiunea - Pagina 4 Png.latex?\tau=-\frac{b}{a^2+b^2}$

Derivând curbura în funcție de raza a și presupunând că pasul b rămâne constant,
$Curbura este egală cu torsiunea - Pagina 4 Png$

deci obținem minunea asta de formulă:
$Curbura este egală cu torsiunea - Pagina 4 Png$

Nu ezitați să comentați, să întrebați, să adăugați, să criticați. Și nu ezitați să dați de veste, distribuind articolul, dacă v-a pus pe gânduri. Mulțumesc!

In cazul unei elice cilindrice avand raza a=ct, si pasul b=ct , inseamna ca derivatele acestor constante sunt egale cu zero. Deci in ultima relatie derivata curburii va fi egala cu zero, adica curbura este o constanta. Ce alta semnificatie se gaseste in aceasta relatie decat ca atat curbura cat si torsiunea sunt constante pentru o elice cilindrica?

Scris de **Abel Cavaşi** Lun 27 Sept 2021, 06:45

virgil a scris:In cazul unei elice cilindrice avand raza a=ct, si pasul b=ct , inseamna ca derivatele acestor constante sunt egale cu zero. Deci in ultima relatie derivata curburii va fi egala cu zero, adica curbura este o constanta. Ce alta semnificatie se gaseste in aceasta relatie decat ca atat curbura cat si torsiunea sunt constante pentru o elice cilindrica?

Adică ce semnificație are faptul că constanța curburii poate fi asigurată de egalitatea dintre curbură și torsiune? Sunt întrebări puerile, puse de cineva care habar nu are cu câte probleme teoretice se confruntă omenirea, cu câte dificultăți s-au confruntat teoreticienii de-a lungul deceniilor pentru a explica, de exemplu, cum se obține stabilitatea sistemelor sau cum se explică turbulența sau atâtea și atâtea mistere...

Scris de **virgil** Lun 27 Sept 2021, 07:45

Abel Cavaşi a scris:
virgil a scris:In cazul unei elice cilindrice avand raza a=ct, si pasul b=ct , inseamna ca derivatele acestor constante sunt egale cu zero. Deci in ultima relatie derivata curburii va fi egala cu zero, adica curbura este o constanta. Ce alta semnificatie se gaseste in aceasta relatie decat ca atat curbura cat si torsiunea sunt constante pentru o elice cilindrica?
Adică ce semnificație are faptul că constanța curburii poate fi asigurată de egalitatea dintre curbură și torsiune? Sunt întrebări puerile, puse de cineva care habar nu are cu câte probleme teoretice se confruntă omenirea, cu câte dificultăți s-au confruntat teoreticienii de-a lungul deceniilor pentru a explica, de exemplu, cum se obține stabilitatea sistemelor sau cum se explică turbulența sau atâtea și atâtea mistere...

La orice elice cilindrica cu pasul constant curbura este constanta. Singurele situatii cand curbura este variabila se intalneste la elicele eliptice.Curbura nu este niciodata egala cu torsiunea, pentru ca sunt doua caracteristici complet diferite. daca curbura este inversul razei de curbura si are ca unitate de masura [1/m], torsiunea reprezinta unghiul de rasucire a triedrului Frenet dealungul traiectoriei raportata pe unitatea de lungime si se masoara in [grad/m], mai exact cu cate grade se rasuceste triedrul Frenet cand punctul considerat de pe traiectorie se deplaseaza cu un metru.
Sa analizam relatia pentru torsiune data de tine; tr=-b/(a^2+b^2); Daca desfasori o elice cilindrica pe un plan, in care raza de curbura a devine axa y si pasul b axa x observam ca lungimea elicei Le pentru un pas devine ipotenuza unui triunghi dreptunghic din care scoatem ca [(2pi.a)^2+b^2]=Le^2; Raportul dintre pasul b si patratul lungimii elicei desfasurate Le, se masoara in [1/m] la fel ca si curbura dar nu are nici o semnificatie fizica legata de torsiune. Si de ce ar purta semnul minus acest raport?

Scris de **Abel Cavaşi** Lun 27 Sept 2021, 12:12

Iar vii cu unitățile de măsură? N-ai înțeles nici acum ce este torsiunea unei curbe? Ferească sfântu'!

Scris de **virgil_48** Lun 27 Sept 2021, 17:32

Abel Cavaşi a scris:Iar vii cu unitățile de măsură? N-ai înțeles nici acum ce este torsiunea unei curbe? Ferească sfântu'!

Decat sa-i spui lui Virgil ca nu a inteles, argument relativ,
mai bine ai clarifica ceva care se poate clarifica usor.
Sa te adancesti in problemele teoretice complicate ale
geometriei este calea cea mai sigura pentru a imprastia
subiectul pana nu se mai stie ce sustii. S-a mai intamplat.
Daca vrei sa elucidezi problema, trebuie sa spui clar ce
inseamna "curbura este egala cu torsiunea" referindu-te
la cei doi parametri, raza si pasul. Acestia sunt singurii!
Ce relatie se creaza in acest caz intre ei ? Ca sa aflam si
noi ce pas are elicea "speciala" care are raza 10 cm.
Altfel acest topic nu are rost.
Daca nu poti clarifica problema, mai bine anunta ca ai inchis
topicul.

Scris de **virgil** Lun 27 Sept 2021, 17:43

Abel Cavaşi a scris:Iar vii cu unitățile de măsură? N-ai înțeles nici acum ce este torsiunea unei curbe? Ferească sfântu'!

Nu uita ce ai scris la inceputul topicului;

Încerc să vă răspund aici la toate întrebările pe care mi le-ați pus în altă parte pe forum. Poate că din acest articol veți reuși să culegeți răspunsurile pe care n-am reușit încă să vi le ofer.
Nu ezitați să comentați, să întrebați, să adăugați, să criticați. Și nu ezitați să dați de veste, distribuind articolul, dacă v-a pus pe gânduri. Mulțumesc!

Te rog sa-mi dai definitia torsiunii unei curbe fara a folosi acea relatie de calcul, poate nu am inteles eu prea bine.

Scris de **Abel Cavaşi** Lun 27 Sept 2021, 22:12

Da, am zis că vă răspund la întrebări, dar, desigur, la cele care au legătură cu subiectul, nu cu lucruri știute deja pe care le puteți găsi în cursuri obișnuite. Pune mânuța pe carte și studiază singur răspunsul la întrebările puerile. Apoi vino să discutăm lucrurile profunde. Topicul acesta nu este pentru a vă iniția în „tainele” torsiunii, ci în alte taine.

Scris de **virgil** Mar 28 Sept 2021, 09:22

Abel Cavaşi a scris:Da, am zis că vă răspund la întrebări, dar, desigur, la cele care au legătură cu subiectul, nu cu lucruri știute deja pe care le puteți găsi în cursuri obișnuite. Pune mânuța pe carte și studiază singur răspunsul la întrebările puerile. Apoi vino să discutăm lucrurile profunde. Topicul acesta nu este pentru a vă iniția în „tainele” torsiunii, ci în alte taine.

Am sa-ti spun eu de ce ocolesti raspunsul, pentruca nu exista nici o definitie in matematica pentru aceasta notiune numita torsiunea curbelor, care nu are absolut nici o legatura cu torsiunea din fizica privind deformarea corpurilor. In timp ce curbura are un sens fizic clar, torsiunea curbelor nu are nici un sens fizic, ci este o denumire a unei expresii matematice care putea fi oricare alta.

Scris de **virgil** Mier 29 Sept 2021, 11:09

Abel Cavaşi a scris:Iar vii cu unitățile de măsură? N-ai înțeles nici acum ce este torsiunea unei curbe? Ferească sfântu'!

In fizica nu exista notiune care sa nu aiba unitate de masura. Asadar daca te gandesti sa folosesti triedrul Frenet la ceva aplicatii in fizica, sa nu scapi din vedere acest lucru, pentru ca totul se masoara.

Scris de Continut sponsorizat

Curbura este egală cu torsiunea

Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea

Re: Curbura este egală cu torsiunea