Ultimele subiecte
» Eu sunt Dumnezeu - viitoarea mea carte in limba romanaScris de Meteorr Astazi la 21:34
» În ce tip de dovezi aveţi încredere deplină?
Scris de virgil Ieri la 20:31
» TEORIA CONSPIRATIEI NU ESTE UN MIT...
Scris de eugen Mar 19 Noi 2024, 21:57
» ChatGPT este din ce în ce mai receptiv
Scris de CAdi Mar 19 Noi 2024, 13:07
» Unde a ajuns stiinta ?
Scris de virgil Sam 16 Noi 2024, 12:00
» OZN in Romania
Scris de virgil Vin 15 Noi 2024, 19:26
» Carti sau documente de care avem nevoie
Scris de virgil Vin 15 Noi 2024, 09:50
» Fiinte deosebite.
Scris de virgil Vin 15 Noi 2024, 09:30
» Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
Scris de virgil Joi 14 Noi 2024, 18:44
» NEWTON
Scris de CAdi Mier 13 Noi 2024, 20:05
» New topic
Scris de ilasus Mar 12 Noi 2024, 11:06
» Pendulul
Scris de Vizitator Vin 08 Noi 2024, 15:14
» Laborator-sa construim impreuna
Scris de eugen Mier 06 Noi 2024, 10:59
» PROFILUL CERCETATORULUI...
Scris de eugen Mier 06 Noi 2024, 07:56
» Ce anume "generează" legile fizice?
Scris de No_name Mar 05 Noi 2024, 19:06
» Ce fel de popor suntem
Scris de eugen Dum 03 Noi 2024, 10:04
» Fenomene Electromagnetice
Scris de virgil Vin 01 Noi 2024, 19:11
» Sa mai auzim si de bine in Romania :
Scris de CAdi Vin 01 Noi 2024, 12:43
» How Self-Reference Builds the World - articol nou
Scris de No_name Mier 30 Oct 2024, 20:01
» Stanley A. Meyer - Hidrogen
Scris de eugen Lun 28 Oct 2024, 11:51
» Daci nemuritori
Scris de virgil Dum 27 Oct 2024, 20:34
» Axioma paralelelor
Scris de No_name Dum 27 Oct 2024, 14:59
» Relații dintre n și pₙ
Scris de No_name Dum 27 Oct 2024, 10:01
» Global warming is happening?
Scris de Meteorr Vin 25 Oct 2024, 23:06
» Atractia Universala
Scris de Meteorr Vin 25 Oct 2024, 23:03
» Despre credinţă şi religie
Scris de Dacu2 Mier 23 Oct 2024, 08:57
» Stiinta oficiala si stiinta neoficiala
Scris de CAdi Vin 18 Oct 2024, 12:50
» țara, legiunea, căpitanul!
Scris de CAdi Vin 18 Oct 2024, 12:37
» Grigorie Yavlinskii
Scris de CAdi Joi 17 Oct 2024, 23:49
» STUDIUL SIMILITUDINII SISTEMELOR MICRO SI MACRO COSMICE
Scris de virgil Joi 17 Oct 2024, 21:37
Postări cu cele mai multe reacții ale lunii
» Mesaj de la virgil în În ce tip de dovezi aveţi încredere deplină? ( 2 )
» Mesaj de la CAdi în În ce tip de dovezi aveţi încredere deplină?
( 2 )
» Mesaj de la No_name în How Self-Reference Builds the World - articol nou
( 1 )
» Mesaj de la CAdi în Care și unde este "puntea" dintre lumea cuantică și cea newtoniană?
( 1 )
» Mesaj de la No_name în Ce anume "generează" legile fizice?
( 1 )
Subiectele cele mai vizionate
Subiectele cele mai active
Top postatori
| virgil (12459) | ||||
| CAdi (12397) | ||||
| virgil_48 (11380) | ||||
| Abel Cavaşi (7963) | ||||
| gafiteanu (7617) | ||||
| curiosul (6790) | ||||
| Razvan (6183) | ||||
| Pacalici (5571) | ||||
| scanteitudorel (4989) | ||||
| eugen (3969) |
Cei care creeaza cel mai des subiecte noi
| Abel Cavaşi | ||||
| Pacalici | ||||
| CAdi | ||||
| curiosul | ||||
| Dacu | ||||
| Razvan | ||||
| virgil | ||||
| meteor | ||||
| gafiteanu | ||||
| scanteitudorel |
Cei mai activi postatori ai lunii
| virgil | ||||
| No_name | ||||
| CAdi | ||||
| ilasus | ||||
| eugen | ||||
| Dacu2 | ||||
| Forever_Man | ||||
| Meteorr | ||||
| Abel Cavaşi |
Cei mai activi postatori ai saptamanii
| Forever_Man | ||||
| virgil | ||||
| Dacu2 | ||||
| CAdi | ||||
| Meteorr | ||||
| ilasus | ||||
| eugen | ||||
| Abel Cavaşi |
Spune şi altora
Cine este conectat?
În total sunt 50 utilizatori conectați: 0 Înregistrați, 0 Invizibil și 50 Vizitatori :: 2 Motoare de căutareNici unul
Recordul de utilizatori conectați a fost de 181, Vin 26 Ian 2024, 01:57
Subiecte similare
Teste propuse la matematică
+5
meteor
CAdi
curiosul
Razvan
Dacu
9 participanți
Pagina 5 din 15
Pagina 5 din 15 •  1, 2, 3, 4, 5, 6 ... 10 ... 15
1, 2, 3, 4, 5, 6 ... 10 ... 15 
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Rezumarea primului mesaj :
Test de matematica:
Sa se gaseasca doua numere naturale consecutive astfel incat impartirea triplului unuia dintre numere la celalalt numar sa dea catul 2 si restul 5.
Test de matematica:
Sa se gaseasca doua numere naturale consecutive astfel incat impartirea triplului unuia dintre numere la celalalt numar sa dea catul 2 si restul 5.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
da da asa e, am adormit la volan, pentru x=4n+3; n>-1 exista o infinitate de solutii.
daca te refereai la aceea ca x e natural
daca te refereai la aceea ca x e natural
meteor- Foarte activ

- Numarul mesajelor : 2203
Data de inscriere : 19/06/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Fără supărare,dar dacă ecuaţiameteor a scris:da da asa e, am adormit la volan, pentru x=4n+3; n>-1 exista o infinitate de solutii.
daca te refereai la aceea ca x e natural
Dacu- Foarte activ

- Numarul mesajelor : 2613
Data de inscriere : 28/07/2012
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Alt test de matematică cu numere complexe:
Să se rezolve ecuaţia unde
unde  .
.
Să se rezolve ecuaţia
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Fără supărare,dar este greşit.Rog a se verifica pentru diferite valori ale luimeteor a scris:x=4n-1, n >=0.
Dacule, pentru ce clasa sunt "testele" acestea?!
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Si de ce nu merge?! Arata atunci unde e gresit.Dacu a scris:
Fără supărare,dar este greşit.Rog a se verifica pentru diferite valori ale lui.
Dacu a scris:
Testele sunt pentru cei din clasaadică a celor care vor să fie acceptaţi în clasa I-a la "Şcoala de cercetare Abel Cavaşi","Secţia de matematică".Mulţumesc!

Pina aici am inteles. Mai departe, in caz ca soarta imi va suride, asa de curiozitate, e cu contract scoala sau nu?!
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Fără supărare,dar de ce s-a impus ca  ?Eu zic că
?Eu zic că  adică
adică  poate fi un număr întreg oarecare.S-a înţeles de ce este greşit?Mulţumesc!
poate fi un număr întreg oarecare.S-a înţeles de ce este greşit?Mulţumesc!
In ce priveşte contractul numai Abel Cavaşi poate zice ceva.
In ce priveşte contractul numai Abel Cavaşi poate zice ceva.
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Da.Dacu a scris:Fără supărare,dar de ce s-a impus ca?Eu zic că
adică
poate fi un număr întreg oarecare.S-a înţeles de ce este greşit?Mulţumesc!
Daca insa se spunea ca x sa apartina lui N, atunci solutia mea era sa fie brici.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Fără supărare,dar atunci când nu se specifică în ce mulţime trebuie rezolvată o ecuaţie asta înseamnă că rezolvitorul trebuie să găsească toate soluţiile posibile.Greşesc eu cumva?Mulţumesc!
Care este deosebirea dintre testul "Să se rezolve ecuaţia unde
unde  ." şi testul "Să se rezolve ecuaţia
." şi testul "Să se rezolve ecuaţia  unde
unde  ."?Ce observăm?Mulţumesc!
."?Ce observăm?Mulţumesc!
Care este deosebirea dintre testul "Să se rezolve ecuaţia
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Tu citesti mesajele mele, sau duci un monolog?!
Eu spun: "Daca era sa se spuna in conditia problemei ca x sa apartina lui N, atunci ar fi fost rezolvarea corecta", tu una si buna o tii.
Ei fie, cu problema mai anterioara, ca nici nu e nevoe sa se specivece carei multimi x apartine, ca ar rezulta din primii termeni ai sirului: x=0,1,2,.., n-1,n.
Asa se face adesea in ziua de azi, INSA, sunt pot fi siruri mai diochete, spre exemplu:
x=0,1,2,7,8,9,14,15,16,21,..., x-7,x-6,x-5,x.
Da, sigur ca in asa cazuri se scriu deja macar primii patru termeni, sau se arata termenii generali.
Eu spun: "Daca era sa se spuna in conditia problemei ca x sa apartina lui N, atunci ar fi fost rezolvarea corecta", tu una si buna o tii.
Ei fie, cu problema mai anterioara, ca nici nu e nevoe sa se specivece carei multimi x apartine, ca ar rezulta din primii termeni ai sirului: x=0,1,2,.., n-1,n.
Asa se face adesea in ziua de azi, INSA, sunt pot fi siruri mai diochete, spre exemplu:
x=0,1,2,7,8,9,14,15,16,21,..., x-7,x-6,x-5,x.
Da, sigur ca in asa cazuri se scriu deja macar primii patru termeni, sau se arata termenii generali.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Fără supărare,dar eu vreau să dialoghez şi am propus nişte teste tocmai ca să vedem cum să le rezolvăm corect şi complet.
---------------------------------
Nu înţeleg cum se poate ca "x=0,1,2,7,8,9,14,15,16,21,..........,x-7,x-6,x-5,x" să fie un şir şi pentru ce valori ale lui x se obţin termenii acestui aşa zis şir?Cum se notează termenii unui şir şi cum se deduc aceştia altfel decât dintr-un singur termen general?Eu ştiu că termenii unui şir sunt unde
unde  .Aştept lămuriri.Mulţumesc!Ce este un şir adică care este definiţia şirului?Greşesc eu cumva cu ceva?Mulţumesc!
.Aştept lămuriri.Mulţumesc!Ce este un şir adică care este definiţia şirului?Greşesc eu cumva cu ceva?Mulţumesc!
---------------------------------
Nu înţeleg cum se poate ca "x=0,1,2,7,8,9,14,15,16,21,..........,x-7,x-6,x-5,x" să fie un şir şi pentru ce valori ale lui x se obţin termenii acestui aşa zis şir?Cum se notează termenii unui şir şi cum se deduc aceştia altfel decât dintr-un singur termen general?Eu ştiu că termenii unui şir sunt
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Test de matematică:
Fie numerele 1,-2,-103,5,....Care este numărul ce urmează?Mulţumesc!
Fie numerele 1,-2,-103,5,....Care este numărul ce urmează?Mulţumesc!
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Fără supărare,dar cum s-a ajuns la acest rezultat?Muţumesc!meteor a scris: 2 ?!
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
nu e 2 e 3!
iar regula e simplă! pentru că nu se specifică care e regula merge și regula că nu e nici o regulă!
adică e din burtă! aleator! cum vrea mușchiul meu!
iar regula e simplă! pentru că nu se specifică care e regula merge și regula că nu e nici o regulă!
adică e din burtă! aleator! cum vrea mușchiul meu!
_________________
linux e gratuit, dar cunoștințele necesare pentru al folosi le acumulezi în timp iar timpul pierdut nu îl poți cumpăra înapoi oricât de mulți bani ai
utilizator linux înregistrat No. 352479
linux counter home page
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Ca un om credincios, eu socot ca tu odata ce intrebi ce numar va fi urmatorul, si daca cineva da un raspuns, tu trebue intii sa spui: asa e, nu e asa. Ci NU sa intrebi: "Dar cum s-a ajuns la acest rezultat?!"Dacu a scris:Fără supărare,dar cum s-a ajuns la acest rezultat?Muţumesc!meteor a scris: 2 ?!
1,-2,-103,5,...
Intuitiv(pot fi si alte interpretari)...Am facut asa: 5-1=4.
La -2 am adunat 4: -2+4=2.
Urmatorul numar va fi -99, apoi 9.
Sirul ar arata asa: 1,-2,-103,5,2,-99,9,6,-93,..
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 15:29, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
După numerele 1,-2,-103,5,....poate urma orice număr.După numerele 1,-2,-103,5,.... poate urma numărul  unde
unde  ?Mulţumesc!
?Mulţumesc!
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
O problema pentru admiterea la grupa pregatitore a scolii de cercetare Abel Cavasi,  .
.
"In geometria euclidiana chite triungiuri sunt mai multe: obtuz unghice sau ascutit unghice, sau invers, sau numarul lor este egal?!
E clar ca numarul lor e infinit, insa careva din ele sunt mai multe la numar, sau nu?!"
"In geometria euclidiana chite triungiuri sunt mai multe: obtuz unghice sau ascutit unghice, sau invers, sau numarul lor este egal?!
E clar ca numarul lor e infinit, insa careva din ele sunt mai multe la numar, sau nu?!"
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 15:29, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Nu este adevărat, infiniturile se pot compara. Nu sunt matematician ca să pot descrie exact cum se face, dar am citit cândva. Ideea este că dacă între două mulțimi ”infinite” se poate stabili o bijecție, atunci se poate număra care mulțime are mai multe elemente. O relație bijectivă este o relație care identifică fiecare element al unei mulțimi în mod unic cu un element al celeilalte mulțimi. Intuitiv, imaginați-vă că avem două turme de vaci și vrem să vedem care turmă are mai multe vaci, deși nu știm să numărăm.
Facem următorul lucru: luăm o vacă din turma 1 și altă vacă din turma 2 și le punem deoparte. Luăm iar o vacă din turma 1 și o vacă din turma 2 și le punem de-o parte, și tot așa. Care turmă se termină prima, aia are mai puține vaci, altfel avem la fel de multe vaci în fiecare turmă.
Matematic, așa se arată destul de simplu că mulțimea numerelor naturale conține la fel de multe numere precum mulțimea numerelor întregi sau mulțimea numerelor raționale. Mai greu se poate arăta că acest număr de elemente este mai mic decât numărul de elemente din mulțimea numerelor reale.
Edit: legat de întrebarea lui meteor, bănuiala mea e că sunt la fel de multe, pe următorul raționament: se poate stabili o bijecție între mulțimea punctelor de pe cercul trigonometric și axa reală, astfel încât putem asocia fiecărui punct al cercului în mod unic un număr real, adică în consecință fiecărui unghi îi putem asocia un unic număr real. Având în vedere că în orice subinterval al mulțimii reale sunt la fel de multe numere ca în întreaga axa reală (ăsta este un rezultat bine știut în matematică), atunci înseamnă că și în intervalul unghiurilor ascuțite sunt la fel de multe numere ca în întervalul unghiurilor obtuze (care-l include pe acesta), deci trebuie să fie la fel de multe triunghiuri și de un fel și de un fel. Nu știu acum să scriu riguros toate astea, dar nu cred că sunt lucruri noi, sigur le găsiți demonstrate temeinic prin cărți de matematică.
Facem următorul lucru: luăm o vacă din turma 1 și altă vacă din turma 2 și le punem deoparte. Luăm iar o vacă din turma 1 și o vacă din turma 2 și le punem de-o parte, și tot așa. Care turmă se termină prima, aia are mai puține vaci, altfel avem la fel de multe vaci în fiecare turmă.
Matematic, așa se arată destul de simplu că mulțimea numerelor naturale conține la fel de multe numere precum mulțimea numerelor întregi sau mulțimea numerelor raționale. Mai greu se poate arăta că acest număr de elemente este mai mic decât numărul de elemente din mulțimea numerelor reale.
Edit: legat de întrebarea lui meteor, bănuiala mea e că sunt la fel de multe, pe următorul raționament: se poate stabili o bijecție între mulțimea punctelor de pe cercul trigonometric și axa reală, astfel încât putem asocia fiecărui punct al cercului în mod unic un număr real, adică în consecință fiecărui unghi îi putem asocia un unic număr real. Având în vedere că în orice subinterval al mulțimii reale sunt la fel de multe numere ca în întreaga axa reală (ăsta este un rezultat bine știut în matematică), atunci înseamnă că și în intervalul unghiurilor ascuțite sunt la fel de multe numere ca în întervalul unghiurilor obtuze (care-l include pe acesta), deci trebuie să fie la fel de multe triunghiuri și de un fel și de un fel. Nu știu acum să scriu riguros toate astea, dar nu cred că sunt lucruri noi, sigur le găsiți demonstrate temeinic prin cărți de matematică.

omuldinluna- Ne-a părăsit
- Mulţumit de forum : Prenume : Omul




Numarul mesajelor : 2728
Puncte : 30680
Data de inscriere : 03/08/2011
Obiective curente : Doresc sa termin expunerea problemei clasice a miscarii in camp central, cu aplicatie la campul gravitational Newtonian
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 15:30, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Așa cum am scris, cardinalul mulțimii numerelor naturale (adică numărul de numere naturale), este diferit de cardinalul mulțimii numerelor reale. Numere naturale sunt  (litera este ”aleph”, prima literă a alfabetului ebraic, indicele 0 datorându-se faptului că este cardinalul celei mai mici mulțimi infinite) la număr, pe când numere reale sunt
(litera este ”aleph”, prima literă a alfabetului ebraic, indicele 0 datorându-se faptului că este cardinalul celei mai mici mulțimi infinite) la număr, pe când numere reale sunt  la număr.
la număr.
Mare lucru în plus n-aș știi să spun. Dacă vrei să aprofundezi, cred că trebuie să începi de aici pentru ideile de bază.
Mare lucru în plus n-aș știi să spun. Dacă vrei să aprofundezi, cred că trebuie să începi de aici pentru ideile de bază.

omuldinluna- Ne-a părăsit
- Mulţumit de forum : Prenume : Omul




Numarul mesajelor : 2728
Puncte : 30680
Data de inscriere : 03/08/2011
Obiective curente : Doresc sa termin expunerea problemei clasice a miscarii in camp central, cu aplicatie la campul gravitational Newtonian
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 15:30, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Mai repet odată (cred că nu se supără nimeni pentru mica abatere, că e un subiect important):
Când ai mulțimi finite, e ușor să vezi care e mai mare sau mai mică, prin procedeul menționat anterior cu cirezile. Asta faci mereu când ”numeri”, spre exemplu când vrei să vezi câte mere ai într-un coș. 1,2,3,4,... până termini merele. În particular, reiese că mulțimea merelor din coș e mai mică decât mulțimea numerelor naturale. Matematicienii au inventat metode pentru a număra și mulțimi infinite, că nu ți se par ție utile sau nu-ți plac, până la urmă te privește, dar asta nu înseamnă că nu există. În contextul întrebării lui meteor, tind să cred că din prisma acestor argumente răspunul tău este greșit (tu spui de fapt că nu are sens, dar are sens deoarece nu conduce la vreo incosistență, compararea infinităților fiind definită în matematică, așa cum am scris). Nu știu sigur nici dacă ce zic eu este corect, stai să caut să văd dacă există o demonstrație.
Am găsit ceva oarecum pe acolo, foarte interesant. Se pare că dacă alegem 3 puncte la întâmplare într-un plan, probabilitatea ca ele să fie vârfurile unui triunghi obtuz este 3/4! Deci din punct de vedere probabilistic, se pare că triunghiurile obtuze sunt mai multe.
Când ai mulțimi finite, e ușor să vezi care e mai mare sau mai mică, prin procedeul menționat anterior cu cirezile. Asta faci mereu când ”numeri”, spre exemplu când vrei să vezi câte mere ai într-un coș. 1,2,3,4,... până termini merele. În particular, reiese că mulțimea merelor din coș e mai mică decât mulțimea numerelor naturale. Matematicienii au inventat metode pentru a număra și mulțimi infinite, că nu ți se par ție utile sau nu-ți plac, până la urmă te privește, dar asta nu înseamnă că nu există. În contextul întrebării lui meteor, tind să cred că din prisma acestor argumente răspunul tău este greșit (tu spui de fapt că nu are sens, dar are sens deoarece nu conduce la vreo incosistență, compararea infinităților fiind definită în matematică, așa cum am scris). Nu știu sigur nici dacă ce zic eu este corect, stai să caut să văd dacă există o demonstrație.
Am găsit ceva oarecum pe acolo, foarte interesant. Se pare că dacă alegem 3 puncte la întâmplare într-un plan, probabilitatea ca ele să fie vârfurile unui triunghi obtuz este 3/4! Deci din punct de vedere probabilistic, se pare că triunghiurile obtuze sunt mai multe.

omuldinluna- Ne-a părăsit
- Mulţumit de forum : Prenume : Omul




Numarul mesajelor : 2728
Puncte : 30680
Data de inscriere : 03/08/2011
Obiective curente : Doresc sa termin expunerea problemei clasice a miscarii in camp central, cu aplicatie la campul gravitational Newtonian
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
...
Ultima editare efectuata de catre curiosul in Vin 08 Feb 2013, 15:30, editata de 1 ori
curiosul- Banat temporar pentru comportamentul nepotrivit
- Mulţumit de forum : Numarul mesajelor : 6790




Puncte : 41551
Data de inscriere : 22/03/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Nu, tocmai în limita în care numărul de încercări tinde la infinit, distribuția se stabilizează la cea prezisă acolo, anume 3/4 ies obtuze și 1/4 ascuțite. Așa funcționează toată statistica. Când faci puține încercări, fluctuațiile sunt mari și e posibil să obții rezultate complet pe dos. Dacă faci numai 4 încercări, poți obține invers, 3 să fie ascuțite și numai 1 obtuz, dar după ce faci 4 miliarde de milioane de încercări, fluctuațiile vor fi infime și vei fi extrem, extrem de aproape de acea distribuție de 3/4 obtuze și 1/4 ascuțite, la care ajungi numai după o infinitate de încercări.
Ce spune de fapt rezultatul acesta este că alegând puncte la întâmplare, triunghiurile obtuze ies mai des ca cele ascuțite. În sensul acesta sunt mai multe. În funcție de câte poți desena concret (ceea ce întreba meteor), cred că răspunsul este cel dat de mine, la fel de multe, anume triunghiuri de fiecare fel. Spun asta pentru că un triunghi ți-l poți imagina ca un triplet de 3 numere reale pozitive (numerele ce corespund fiecărui unghi), deci până la urmă ca un vector din
triunghiuri de fiecare fel. Spun asta pentru că un triunghi ți-l poți imagina ca un triplet de 3 numere reale pozitive (numerele ce corespund fiecărui unghi), deci până la urmă ca un vector din  , ce are tot cardinalitatea lui
, ce are tot cardinalitatea lui  .
.
Ce spune de fapt rezultatul acesta este că alegând puncte la întâmplare, triunghiurile obtuze ies mai des ca cele ascuțite. În sensul acesta sunt mai multe. În funcție de câte poți desena concret (ceea ce întreba meteor), cred că răspunsul este cel dat de mine, la fel de multe, anume

omuldinluna- Ne-a părăsit
- Mulţumit de forum : Prenume : Omul




Numarul mesajelor : 2728
Puncte : 30680
Data de inscriere : 03/08/2011
Obiective curente : Doresc sa termin expunerea problemei clasice a miscarii in camp central, cu aplicatie la campul gravitational Newtonian
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
@curiosule, despre infinit(mare sau mic) mare lucru nici eu nu stiu. Mare lamuriri nu aduc, ca mii frica sa nu imi pirlesc mina.
Intre 2 numere naturale consecutiva sunt o infinitate de numere rationale si o infinitate de numere irationale.
La o prima vedere, presupun ca numerele irationale is mai multe ca numerele rationale.
Un lucru era sa fie foarte bun, daca continuai sa analizezi cercul (trigonometric).
Rezolvare :

Intii definim ce e triunghiul:
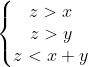
Adica incheem un contract prin care ne intelegem ca z e latura cea mare, nu exista triunghiuri nule.
Acum un lucru important: era o teorema care spunea ca toate triunghiurile au un punct pe arcul cercului, iar celelalt 2 puncte stau la capetele diametrului, atunci punctul ce sta pe arc este unghi drept.
Apoi am tras linia de simetrie OB, apoi... etc.
Ca sa aflam cite triunghiuri is mai multe: obtuzunghice sau ascutitunghice, sau invers, sau daca is egale. Nu ne ramine nimic alceva de facut decit de vazut care arie este mai mare A1(sectorul AOC) sau A2(sectorul ACB).
Dupa ceva calcule: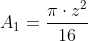 ;
;
}{48}) .
.
Ramine de comparat, aproximind pe PI cu 3.14 si aproximind pe sqrt(3) cu citeva zecimale aflam ca:
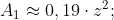 ;
;
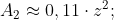
Evident ca triunghiurile obtuzunghice sunt mai multe ca triunghiurile ascutitunghice.
Ca sa aflam cu cit, vom scadea, dar nu are sens caci raspunsul va fi unul: cu infinit mai mult.
Insa putem afla de cite ori sunt mai multe triunghiurile obtuzunghice ca cele ascutitunghice, pentru aceasta efectuam raportul dintre valorile lor si aflam ca:
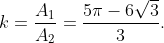 .
.
O alta rezolvare, posibil mai riguroasa ca cea de sus :


Acelasi contract avem, la fel z e cea mai mare latura...:
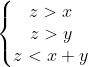
Acum atentie!
1. Arcul pe AC se afla triunghiurile dreptunghice(care nu sunt nici ascutite nici obtuze).
2. In punctul A la fel nu este vorba de nici un triunghi.
3. Pe arcul AB nu se afla nici un triunghi (ascutit unghic), deoarece ar insemna ca mai exista o latura de aceeasi lungime z, care insa incalca contractul nostru.
Deci locul triunghiurilor obtuzunghice se afla pe sectorul ACO, INSA NU includ arcul AC.
La fel locul triunghiurilor ascutitunghice se afla pe sectorul ABC, INSA NU includ arcul AC si AB.
Lungimea ON=z/2;
Lungimea AO (o mai numesc raza mica- r)=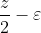 , cu
, cu  am notat o vecinatate (o lungime cea mai mica, altfel spus este grosimea arcului AC) [nu stiu daca e permis de jucat cu asa jucarii, care e matimatician cu palarie mare nu e rau sa ne lumineze putin].
am notat o vecinatate (o lungime cea mai mica, altfel spus este grosimea arcului AC) [nu stiu daca e permis de jucat cu asa jucarii, care e matimatician cu palarie mare nu e rau sa ne lumineze putin].
Dupa calcule ajungem la:
}{16}) ;
;
^{2}arctg(\frac{(\sqrt{3z^{2}-8z\varepsilon +4\varepsilon ^{2}})}{z})}{360}-\frac{\pi (z^{2}+4z\epsilon +4\epsilon ^{2})}{16}-\frac{z\sqrt{3z^{2}-8z\varepsilon }+4\varepsilon ^{2}}{8}) . [poate fi pe undeva sa fi scapat vreo greseala mecanica, in orice caz aveti desenul].
. [poate fi pe undeva sa fi scapat vreo greseala mecanica, in orice caz aveti desenul].
Comparatia va ramine pe seama voastra.
Acum sa facem o generalizare. Punem in joc si triunghiurile nule, si dreptunghice si isoscele (toate) si isoscele (obtuze) si isoscele (ascutite).
Din desen aflam ca:
1) Tr.obtz > Tr. ascut. > Tr. dreptung. > Tr. nule = Tr. isoscele (atit obtuz. cit si isosc.).
2) Tr.obtz > Tr. ascut. > Tr. dreptung. > Tr. nule > Tr. isosc. obtz. > Tr.isosc. acut.
Cred ca e simplu: intre 2 numere naturale consecutive sunt o infinitate de numere rationale.omuldinluna a scris:
Matematic, așa se arată destul de simplu că mulțimea numerelor naturale conține la fel de multe numere precum mulțimea numerelor întregi sau mulțimea numerelor raționale.
Eu cred ca este inca mai simplu.omuldinluna a scris: Mai greu se poate arăta că acest număr de elemente este mai mic decât numărul de elemente din mulțimea numerelor reale.
Intre 2 numere naturale consecutiva sunt o infinitate de numere rationale si o infinitate de numere irationale.
La o prima vedere, presupun ca numerele irationale is mai multe ca numerele rationale.
Nu am inteles cum ai vrea sa pornesti demonstratia.omuldinluna a scris:
Edit: legat de întrebarea lui meteor, bănuiala mea e că sunt la fel de multe, pe următorul raționament: se poate stabili o bijecție între mulțimea punctelor de pe cercul trigonometric și axa reală, astfel încât putem asocia fiecărui punct al cercului în mod unic un număr real, adică în consecință fiecărui unghi îi putem asocia un unic număr real. Având în vedere că în orice subinterval al mulțimii reale sunt la fel de multe numere ca în întreaga axa reală (ăsta este un rezultat bine știut în matematică), atunci înseamnă că și în intervalul unghiurilor ascuțite sunt la fel de multe numere ca în întervalul unghiurilor obtuze (care-l include pe acesta), deci trebuie să fie la fel de multe triunghiuri și de un fel și de un fel. Nu știu acum să scriu riguros toate astea, dar nu cred că sunt lucruri noi, sigur le găsiți demonstrate temeinic prin cărți de matematică.
Un lucru era sa fie foarte bun, daca continuai sa analizezi cercul (trigonometric).
Eu nu ma supar, insa la intrebarea despre misteriosul infinit(mic si mare) cred ca e bine sa se deschida un subiect separat.omuldinluna a scris:
Mai repet odată (cred că nu se supără nimeni pentru mica abatere, că e un subiect important):
Rezolvare :

Intii definim ce e triunghiul:
Adica incheem un contract prin care ne intelegem ca z e latura cea mare, nu exista triunghiuri nule.
Acum un lucru important: era o teorema care spunea ca toate triunghiurile au un punct pe arcul cercului, iar celelalt 2 puncte stau la capetele diametrului, atunci punctul ce sta pe arc este unghi drept.
Apoi am tras linia de simetrie OB, apoi... etc.
Ca sa aflam cite triunghiuri is mai multe: obtuzunghice sau ascutitunghice, sau invers, sau daca is egale. Nu ne ramine nimic alceva de facut decit de vazut care arie este mai mare A1(sectorul AOC) sau A2(sectorul ACB).
Dupa ceva calcule:
Ramine de comparat, aproximind pe PI cu 3.14 si aproximind pe sqrt(3) cu citeva zecimale aflam ca:
Evident ca triunghiurile obtuzunghice sunt mai multe ca triunghiurile ascutitunghice.
Ca sa aflam cu cit, vom scadea, dar nu are sens caci raspunsul va fi unul: cu infinit mai mult.
Insa putem afla de cite ori sunt mai multe triunghiurile obtuzunghice ca cele ascutitunghice, pentru aceasta efectuam raportul dintre valorile lor si aflam ca:
O alta rezolvare, posibil mai riguroasa ca cea de sus :


Acelasi contract avem, la fel z e cea mai mare latura...:
Acum atentie!
1. Arcul pe AC se afla triunghiurile dreptunghice(care nu sunt nici ascutite nici obtuze).
2. In punctul A la fel nu este vorba de nici un triunghi.
3. Pe arcul AB nu se afla nici un triunghi (ascutit unghic), deoarece ar insemna ca mai exista o latura de aceeasi lungime z, care insa incalca contractul nostru.
Deci locul triunghiurilor obtuzunghice se afla pe sectorul ACO, INSA NU includ arcul AC.
La fel locul triunghiurilor ascutitunghice se afla pe sectorul ABC, INSA NU includ arcul AC si AB.
Lungimea ON=z/2;
Lungimea AO (o mai numesc raza mica- r)=
Dupa calcule ajungem la:
Comparatia va ramine pe seama voastra.
Acum sa facem o generalizare. Punem in joc si triunghiurile nule, si dreptunghice si isoscele (toate) si isoscele (obtuze) si isoscele (ascutite).
Din desen aflam ca:
1) Tr.obtz > Tr. ascut. > Tr. dreptung. > Tr. nule = Tr. isoscele (atit obtuz. cit si isosc.).
2) Tr.obtz > Tr. ascut. > Tr. dreptung. > Tr. nule > Tr. isosc. obtz. > Tr.isosc. acut.
Ultima editare efectuata de catre meteor in Mar 04 Dec 2012, 21:31, editata de 1 ori (Motiv : am eliminat unele expresii cu caracter comic)
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Iata am observat o greseala mecanica care am facut-o si in desen.
La partea a doua (pentru matematica mai serioasa).
La fel trebuia ca ON sa fie egal cu AO=z/2-e [m-a incurcat a naibii linia aia de simetrie].
Deci si calculele putin is altfel.
La partea a doua (pentru matematica mai serioasa).
La fel trebuia ca ON sa fie egal cu AO=z/2-e [m-a incurcat a naibii linia aia de simetrie].
Deci si calculele putin is altfel.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Si inca una...(tot la matematica cea creata).
Atunci cind am calculat aria lui AOB, am uitat sa scad aria sectorului de cerc a lui AOC (putin mai mare..), CARE NU mai are raza nici z/2 si nici r=z/2-e, ci z/2+e.
Atunci cind am calculat aria lui AOB, am uitat sa scad aria sectorului de cerc a lui AOC (putin mai mare..), CARE NU mai are raza nici z/2 si nici r=z/2-e, ci z/2+e.
meteor- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2203




Puncte : 25843
Data de inscriere : 19/06/2011
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Numărul triunghiurilor ascuţitunghice este egal cu numărul triunghiurilor obtuzunghice şi aceasta nu este o problemă de probabilitate. 
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
 Re: Teste propuse la matematică
Re: Teste propuse la matematică
Test de matematică privind inecuaţiile:
Să se rezolve inecuaţia^2<0}) .
.
Să se rezolve inecuaţia
Dacu- Foarte activ

- Mulţumit de forum : Numarul mesajelor : 2613




Puncte : 22430
Data de inscriere : 28/07/2012
Obiective curente : Acum mă preocupă următoarele:-1)...-2)...
Pagina 5 din 15 •  1, 2, 3, 4, 5, 6 ... 10 ... 15
1, 2, 3, 4, 5, 6 ... 10 ... 15 
Pagina 5 din 15
Permisiunile acestui forum:
Nu puteti raspunde la subiectele acestui forum



 Devino fan Forumgratuit
Devino fan Forumgratuit 